Презентация "Решение задач по комбинаторике и теории вероятности."

Решение различных задач по комбинаторике и теории вероятности

Справочный материал

Вероятностью события А называется отношение

числа благоприятных для него исходов испытания к

числу всех равновозможных исходов.

где m - число исходов, благоприятствующих

осуществлению события,

а n - число всех возможных исходов.

Некоторые формулы

• Вероятность достоверного события равна единице.
• Вероятность невозможного события равна нулю.
• Сумма вероятностей противоположных событий равна 1.

• Формула сложения вероятностей совместных событий:

P(A U B)   =P(A) + P(B) – P(A∩B)

5 . Вероятность появления одного из двух несовместных

событий равна сумме вероятностей этих событий.   

P(A U B)   =P(A) + P(B)          

6. Вероятность произведения независимых событий А и В

(наступают одновременно)вычисляется по формуле: 

P(A∩B) = P(A) ∙ P(B) .

7. Формула умножения вероятностей:

                         P(A∩B) = P(A) ∙ P(B/A) ,

где P(B/A) – условная вероятность события В,

при условии, что событие А наступило .

8. Формула Бернулли – формула вероятности k успехов в

серии из n испытаний

где – число сочетаний,

р – вероятность успеха,

q = 1 – р – вероятность неудачи.

При подбрасывании симметричной монеты, когда р = q = ½ , формула Бернулли принимает вид:

Например, вероятность выпадения орла дважды в трех испытаниях:

Методы решения задач

• С помощью классической формулы вероятности:

1.Папа, мама, сын и дочка бросили жребий – кому мыть

посуду. Найдите вероятность того, что посуду будет

мыть мама.           

Решение

n = 4 – число всех элементарных исходов;

m = 1 – число благоприятных исходов

(жребий выпал на маму).

Ответ: 0,25

2. Женя, Лена, Маша, Аня и Коля бросили жребий – кому идти в магазин. Найдите вероятность того, что в магазин надо будет идти Ане.

Решение

n = 5 – число всех возможных исходов;

m = 1 – число благоприятных исходов

(в магазин идти Ане).

Ответ: 0,2

3. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 8 сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Решение

n = 100 + 8 = 108 – число всех возможных исходов (всего сумок);

m = 1 00 – число благоприятных исходов (качественная сумка).

Ответ: 0,93

4. В среднем из 1000 садовых насосов, поступивших в продажу, 9 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение

n = 1000 – число всех возможных исходов

(всего насосов);

m = 1 000 – 9 = 991 – число благоприятных

исходов (насос не подтекает).

Ответ: 0,991

5. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.

Решение

n = 55 – число всех возможных

исходов;

m = 1 1 – число благоприятных

исходов (вопрос по ботанике).

Ответ: 0,2

6. На семинар приехали трое ученых из Норвегии, четверо из России и трое из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.

Решение

n = 3+4+3=10 – число всех возможных исходов,

(число всех претендентов на это,

в данном случае восьмое, место);

m = 4 – число благоприятных исходов

(число претендентов из России).

Ответ: 0,4

7. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.

Решение

n = 20 – число всех возможных

исходов,(число всех претендентов на

это место, причем это может

быть1, 2, …, 8, последнее место);

m = 20 – (8+7)=5 – число благоприятных

исходов (число претендентов из Китая)

Ответ: 0,25

8. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений  – по одному от каждой страны. В первый

день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Решение

n = 80 – число всех возможных исходов

(всех возможных порядковых номеров

выступления представителя России);

m = (80-8): 4 = 18 – число благоприятных

исходов (порядковых номеров, приходящихся

на второй, третий , четвертый и пятый дни).

Ответ: 0,225

9. В чемпионате мира участвуют 20 команд. С помощью жребия их нужно разделить на четыре группы по пять команд в каждой. В ящике вперемешку лежат карточки с номерами групп: 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 . Капитаны команд тянут по карточке. Какова вероятность того, что команда Великобритании окажется во второй группе?

Решение

n = 20 – число всех возможных

исходов (всего карточек);

m = 5 – число благоприятных исходов

(число карточек с номером 2).

Ответ: 0 ,25

10. Перед началом первого тура чемпионата по

Бадминтону участников разбивают на игровые пары

случайным образом с помощью жребия. Всего в чемпионате

участвует 26 бадминтонистов, среди которых 10

участников из России, в том числе Руслан Орлов. Найдите

вероятность того, что в первом туре Руслан Орлов будет

играть с каким-либо бадминтонистом из России?

Решение

n = 26 – 1 = 25 – число всех возможных исходов

(число соперников);

m = 10 – 1 = 9 – число благоприятных исходов

(число соперников-россиян);

Сам с собой он играть не будет!

Ответ: 0,36

11. Перед началом первого тура чемпионата по шахматам

участников разбивают на игровые пары случайным образом с

помощью жребия. Всего в чемпионате участвует 76

шахматистов, среди которых 4 участника из России, в том

числе Александр Ефимов. Найдите вероятность того, что в

первом туре Александр Ефимов будет играть с каким-либо

шахматистом из России

Решение

n = 76 – 1 = 75 – число всех возможных исходов

(число соперников),

m = 4 – 1 = 3 – число благоприятных исходов

(число соперников-россиян)

Ответ: 0,04

12. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом

с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 участников из России, в

том числе Ярослав Исаков. Найдите вероятность того,

что в первом туре Ярослав Исаков будет играть с каким-либо теннисистом из России?

Решение

n = 46 – 1 = 45 – число всех возможных исходов

(равно числу соперников)

m = 19 – 1 = 18 – число благоприятных исходов

(при которых соперником будет россиянин)

Ответ: 0,4

2 . Метод перебора комбинаций

Задачи с монетами ( и игральной костью) при небольшом

количестве подбрасываний удобно решать методом перебора

комбинаций.

– выписываем все возможные комбинации орлов и решек.

Например, ОО,ОР,РО, РР. Число таких комбинаций – n;

– среди полученных комбинаций выделяем те, которые

требуются по условию задачи (благоприятные исходы), – m ;

– вероятность находим по формуле:

13. Бросают игральную кость. Найдите вероятность

того, что выпадет число, меньшее 4 очков.

Решение

n = 6 – число всех возможных исходов (выпадение чисел 1, 2, 3, 4, 5, 6);

m = 3 – число благоприятных исходов (выпадение чисел 1, 2, 3).

Ответ: 0,5

14. Игральную кость (кубик) бросили один раз. Какова

вероятность того, что выпало нечетное число очков?

Решение

n = 6 – число всех возможных исходов

(выпадение чисел 1, 2, 3, 4, 5, 6),

m = 3 – число благоприятных исходов (выпадение чисел 1, 3, 5)

Ответ: 0,5

15. В случайном эксперименте бросают две игральные

кости. Найдите вероятность того, что в сумме выпадет 8

очков. Результат округлите до сотых.

Решение

I способ

n = 6*6 = 36 – число всех возможных исходов

(выпадение чисел на двух кубиках:

{ 1,1 } {1 ,2 } {1 ,3 } {1 ,4 } {1 ,5 } {1 ,6 }

{2 ,1 } {2 ,2 } {2 ,3 } {2 ,4 } {2 ,5 } {2 ,6 }

…

{6 ,1 } {6 ,2 } {6 ,3 } {6 ,4 } {6 ,5 } {6 ,6 }) ;

m = 5 – число благоприятных исходов (выпадение чисел {2 , 6} {3 , 5} {4 , 4} {5 , 3} {6 , 2}) .

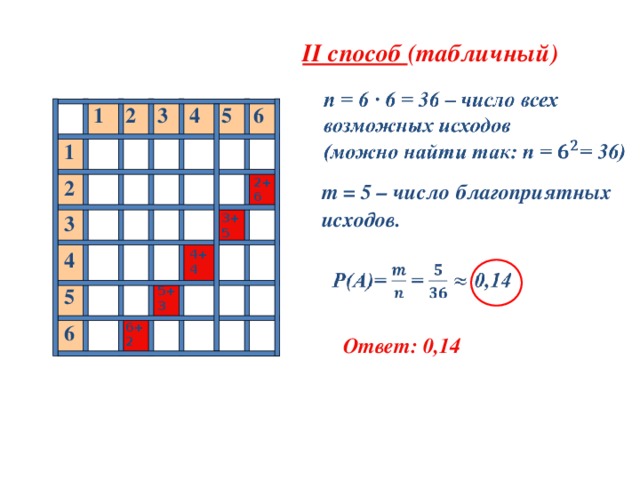
II способ (табличный)

1

1

2

2

3

3

4

4

5

5

6

6

2+6

6+2

4+4

5+3

3+5

m = 5 – число благоприятных

исходов.

Ответ: 0,14

16.Лена дважды бросает игральный кубик. В сумме у нее

выпало 11 очков. Найдите вероятность того, что при

втором броске выпало 6 очков.

Решение

При бросании кубика 11 очков можно получить двумя

способами 5+6 или 6+5 .

n = 2 – число всех возможных исходов, {5 ,6 } {6 ,5 } ;

m = 1 – число благоприятных исходов, {5 ,6 } .

Ответ: 0,5

17. Женя дважды бросает игральный кубик. В сумме у нее

выпало 5 очков. Найдите вероятность того, что при

втором броске выпало 2 очка.

Решение

При бросании кубика 5 очков можно получить четырьмя способами.

n = 4 – число всех возможных исходов

{ 1,4 } { 2,3 } { 3,2 } { 4,1 } ;

m = 1 – число благоприятных исходов, { 3,2 } .

Ответ: 0,25

18. Наташа и Вика играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. В сумме выпало 9 очков. Найдите вероятность того, что Наташа проиграла.

Решение

При бросании кубика 9 очков можно получить четырьмя способами: 3+6 , 4+5, 5+4, 6+3;

n = 4 – число всех возможных исходов, { 3,6 } { 4,5 } {5 ,4 } {6 ,3 } ;

m = 2 – число исходов, при которых у Наташи (на первом

кубике) выпало меньше очков, чем у Вики.

Ответ: 0,5

19. Тоша и Гоша играют в кости. Они бросают кубик по

одному разу. Выигрывает тот, кто выбросил больше очков.

Если очков выпало поровну, то наступает ничья. Первым

бросил Тоша, у него выпало 3 очка. Найдите вероятность

того, что Гоша не выиграет.

Решение

При условии, что у Тоши выпало 3 очка, возможны

исходы: { 3,1 } { 3,2 } { 3,3 } { 3,4 } { 3,5 } { 3,6 } ;

n = 6 – число всех возможных исходов;

m = 3 – число исходов, при которых Гоша не выиграет, т.е.

наберет 1, 2 или 3 очка.

Ответ: 0,5

20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Решение

I способ (метод перебора комбинаций)

Монету бросают 2 раза.

Обозначения: О – выпадение орла, Р – выпадение

решки, { О Р } - выпадение орла в первом броске,

решки – во втором.

{ О О }

{ О Р }

{ Р О }

{ Р Р }

n = 4 – число всех возможных исходов:

m = 2 – число благоприятных исходов

(выпадение орла ровно один раз)

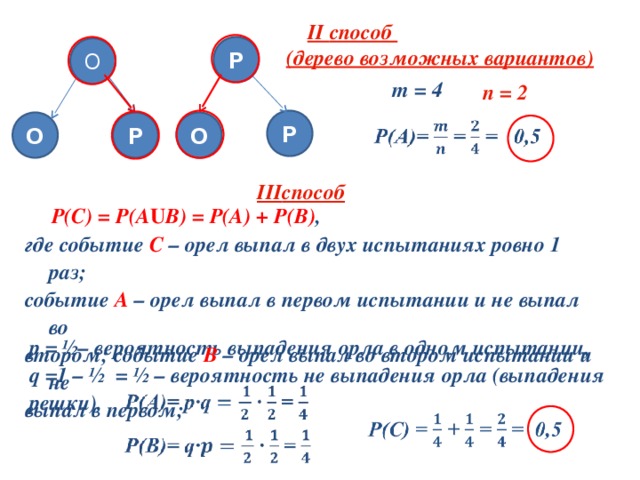
II способ

(дерево возможных вариантов)

Р

О

n = 2

m = 4

Р

Р

О

О

III способ

Р(С) = Р(А U В) = Р(А) + Р(В) ,

где событие С – орел выпал в двух испытаниях ровно 1 раз;

событие А – орел выпал в первом испытании и не выпал во

втором; событие В – орел выпал во втором испытании и не

выпал в первом;

р = ½ – вероятность выпадения орла в одном испытании,

q =1 – ½ = ½ – вероятность не выпадения орла (выпадения

решки).

IV способ

По формуле Бернулли

вероятность одного успеха (к=1)

в двух испытаниях ( n =2), если

р = ½ – вероятность выпадения орла в одном испытании,

q =1 – ½ = ½ – вероятность не выпадения орла (выпадения

решки).

Или по второй формуле:

Ответ: 0,5

21.Перед началом матча по футболу судья бросает монету,

чтобы определить, какая из команд будет первой владеть

мячом. Команда «Меркурий» играет по очереди с командами

«Марс», «Юпитер», «Уран». Найти вероятность того, что

во всех матчах право владеть мячом получит команда

«Меркурий». 

Решение

I способ (перебора комбинаций)

Монету бросают 3 раза.

Для команды «Меркурий»

возможные исходы в трех бросках →

{ О О О }

{ Р О О }

{ О Р О }

{ О О Р }

{ Р Р О }

{ Р О Р }

{ О Р Р }

{ Р Р Р }

n = 8 – число всех возможных исходов;

m = 1 – число благоприятных

исходов (выпадение орла в трех

бросках).

II способ

По формуле Бернулли вероятность трех успехов (к = 3)

в трех испытаниях ( n = 3):

III способ

Применим правило умножения вероятностей независимых событий.

Вероятность выпадения орла в каждом случае равна ½ . Значит, вероятность того, что орел выпадет все три раза, равна:

Ответ: 0,125

22.Перед началом матча по футболу судья бросает монету,

чтобы определить, какая из команд будет первой владеть

мячом. Команда «Байкал» играет по очереди с командами

«Амур», «Енисей», «Иртыш». Найти вероятность того, что

команда «Байкал» будет первой владеть мячом только в игре с «Амуром».

{ О О О }

{ Р О О }

{ О Р О }

{ О О Р }

{ Р Р О }

{ Р О Р }

{ О Р Р }

{ Р Р Р }

Решение

Монету бросают 3 раза.

Для команды «Байкал»

возможные исходы в трех бросках →

n = 8 – число всех возможных исходов;

m = 1 – число благоприятных исходов

(выпадение орла в первой игре).

Ответ: 0,125

23. У Пети в кармане лежат шесть монет: четыре монеты по рублю и две монеты по два рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что теперь две двухрублевые монеты лежат в одном кармане.

Решение

I способ (метод перебора вариантов):

{ 234 }

{ 235 }

{ 236 }

{ 245 }

{ 246 }

{ 256 }

{ 345 }

{ 346 }

{ 356 }

{ 456 }

{ 123 }

{ 124 }

{ 125 }

{ 126 }

{ 134 }

{ 135 }

{ 136 }

{ 145 }

{ 146 }

{ 156 }

Пронумеруем монеты: рублевые – 1, 2, 3, 4;

двухрублевые – 5, 6.

n = 20 – число всех исходов

Взять три монеты можно так:

( числа в порядке возрастания,

чтобы не пропустить комбинацию) →

m = 8 – число благоприятных исходов

(комбинации, в которых монеты 5 и 6

(двухрублевые) не взяты или взяты обе)

II способ (комбинаторный):

Р(С) = Р(А) + Р(В) , где событие С – двухрублевые монеты лежат в одном кармане;

событие А – двухрублевые монеты остались в кармане, а переложил рублевые;

событие В – переложил обе двухрублевые монеты и одну рублевую;

события А и В несовместные.

III способ (непосредственного вычисления вероятности):

Монеты окажутся в одном кармане, если переложены три

рублевые или две рублевые и одна двухрублевая монета.

Переложить их последовательно можно четырьмя

способами ( обозначения: рублевая – 1, двухрублевая – 2) :

1 1 1

1 2 2

2 2 1

2 1 2

Ответ: 0,4

24.У Пети в кармане лежат шесть монет: четыре монеты по рублю и две монеты по два рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что теперь две двухрублевые монеты лежат в разных карманах.

Решение

{ 234 }

{ 235 }

{ 236 }

{ 245 }

{ 246 }

{ 256 }

{ 345 }

{ 346 }

{ 356 }

{ 456 }

{ 123 }

{ 124 }

{ 125 }

{ 126 }

{ 134 }

{ 135 }

{ 136 }

{ 145 }

{ 146 }

{ 156 }

I способ (метод перебора вариантов):

Пронумеруем монеты: рублевые – 1, 2, 3, 4;

двухрублевые – 5, 6.

n = 20 – число всех исходов

Взять три монеты можно так:

( числа в порядке возрастания,

чтобы не пропустить комбинацию) →

m = 12 – число благоприятных исходов

(комбинации, в которых монеты 5 и 6

(двухрублевые) взяты по одной)

II способ (комбинаторный)

Событие А - переложили две рублевые монеты и одну

двухрублевую.

III способ

Монеты окажутся в разных карманах, если переложены

две рублевые и одна двухрублевая монета.

Переложить их последовательно можно тремя способами:,

1 1 2

1 2 1

2 1 1

Ответ: 0,6

25. Найти вероятность того, что произведение трех последних цифр случайно выбранного телефонного номера четно .

Решение

I способ

II способ

m = (5 ∙ 5 ∙ 5)∙ 3 + (5 ∙ 5 ∙ 5)∙ 3 + ( 5 ∙ 5 ∙ 5 ) = 875

(5 ∙ 5 ∙ 5)∙ 3 – количество исходов, когда одна цифра четная, а

две другие нечетные (для каждой цифры исходов – 5,

вариантов расположения – 3).

(5 ∙ 5 ∙ 5)∙ 3 – количество исходов, когда две цифры четные, а

одна – нечетная,

5 ∙ 5 ∙ 5 – количество исходов, когда все три цифры – четные.

n = 10 ∙ 10 ∙ 10 = 1000 – количество всех исходов ( для каждой

цифры – 10)

III способ

IV способ

Выбор четной или нечетной цифры можно сравнить

с выпадением орла или решки при подбрасывании монеты

несколько раз с такой же вероятностью. Тогда выбор трех

нечетных цифр аналогичен выпадению трех решек в трех

испытаниях

Ответ: 0,875

Комбинаторный метод решения можно применять

при подсчете количества исходов с помощью формул

комбинаторики.

26.Биатлонист пять раз стреляет по мишеням.

Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые четыре раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

Решение

Вероятность попадания в мишень равна 0,7;

вероятность промаха равна 1 – 0,7 = 0,3.

Т. к. результаты выстрелов – независимые события, вероятность того, что биатлонист четыре раза попал в мишень, а один раз промахнулся, равна:

Р= 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,3 ≈ 0,07

Ответ: 0,07

27. В магазине стоят три платежных автомата. Каждый из них может быть неисправен с вероятностью 0,1. Найдите вероятность того, что хотя бы один автомат исправен.

Решение

Тогда Р(А)= 1 - 0,001 = 0,999

Ответ: 0,999

29. В интернет-магазине три телефонных оператора. В случайный момент оператор занят разговором с клиентом с вероятностью 0,7 независимо от других. Клиент звонит в магазин. Найдите вероятность того, что в этот момент хотя бы один оператор не занят.

Решение

I способ

Событие А – не занят хотя бы один оператор,

т.е. не занят один, два или все три оператора.

Р(А) = (0,3 ∙ 0,7 ∙ 0,7) ∙ 3 + (0,3 ∙ 0,3 ∙ 0,7) ∙ 3 +

+ 0,3 ∙ 0,3 ∙ 0,3 = 0,657

II способ

Ответ: 0,657

29.В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы . Найдите вероятность того, что Тоша и Гоша попали в одну группу.

Решение

Ответ: 0,3

30. В классе 28 учащихся, среди них Наташа и Владик - брат и сестра. Для проведения медосмотра класс случайным образом разбивают на 2 равные группы. Найти вероятность того, что Владик и Наташа попали в разные группы.

Решение

31. В группе иностранных туристов 51 человек. Среди них два испанца. Для посещения музея группу делят на две подгруппы – 25 и 26 человек – случайным образом. Найти вероятность того, что оба испанца окажутся в одной подгруппе.

Решение