Презентация "Теорема Пифагора"

«Помогла теорема Пифагора»

Суть истины вся в том, что нам она – навечно

Когда хоть раз в прозрении ее увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна…

А. Шамиссо

урок геометрии в 8 классе

«Геометрия владеет двумя сокровищами: одно из них – теорема Пифагора, другое - золотое сечение, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Иоганн Кеплер

Разминка

Назовите гипотенузу

и катеты и запишите соответствующие равенства

• КD-высота

К

N

М

D

Найдите острый угол

45 0

60 0

20 0

30 0

45 0

70 0

• Найти BC

• Найти MN

В

N

12см

15см

60 0

30 0

К

М

С

А

Ответ:BC=7,5см

Ответ:MN=6см

А

В

С

2,4см

4,8см

Найти угол А и угол С

Ответ: ∟ A=30 0 , ∟ C=60 0

Блиц –опрос.

1)Один из углов прямоугольного треугольника равен 25⁰. Чему равны остальные углы?

2)Один из углов прямоугольного треугольника равен 30⁰, катет противолежащий ему, равен 11 см. Чему равна гипотенуза?

3)Катет прямоугольного треугольника равен 6 дм, гипотенуза равна 12 дм. Найдите углы треугольника?

4) Сторона квадрата равна 1,5 м. Найдите площадь квадрата?

5)Если сторона квадрата равна 13 см, то чему равна его площадь?

6)Площадь квадрата равна 121 см 2 , чему равна сторона квадрата?

7) Катеты прямоугольного треугольника равны 5 и 8 см. Найдите площадь прямоугольного треугольника?

8)Площадь квадрата равна 5 см. Найдите длину стороны квадрата

9)Площадь равнобедренного прямоугольного треугольника равна 4,5 см. Найдите катеты этого треугольника.

10)Площадь квадрата равна -36 см 2 . найдите длину стороны квадрата .

Результаты блиц-опроса

1)65⁰, 90 0

2)22см

3)30⁰,60⁰

4)2,25 м 2

5)169 см 2

6)11 см

7)20 см 2

8)

9) 3 и 3 см

10)задача не имеет решения

Постройте прямоугольный треугольник с данными катетами и измерьте гипотенузу

a

Историки

b

Теоретики

12

Практики

c

6

5

8

3

4

Постройте прямоугольный треугольник с данными катетами и измерьте гипотенузу

a

Историки

b

Теоретики

12

Практики

c

6

5

3

8

13

4

10

5

Выразите зависимость между длинами катетов и гипотенузой

a 2

Историки

Теоретики

b 2

144

c 2

Практики

36

25

169

9

64

16

100

25

Историки.

ПИФАГОР.

Жизнь и учение .

Портреты Пифагора

Родина ученого

Остров Самос

Жизненный путь Пифагора

Вавилон

Египет

Греция

(о. Самос)

Жизненный путь Пифагора

Южная Италия

(г. Кротон)

Греция

(о. Самос)

Школа Пифагора

За светлый луч с небес вознес благодаренье…

Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины. Так художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»

Картина передает пафос преклонения учеников легендарной школы перед единой гармонией, царящей в мироздании («космосе»), музыке и числе.

Заповеди Пифагора

и его учеников актуальны и сейчас и могут быть

приемлемы для любого здравомыслящего человека.

Вот они!

Заповеди пифагорийцев

• Делать то, что впоследствии не огорчит тебя и не принудит раскаиваться;
• Не делай никогда того, что не знаешь, но научись всему, что следует знать;
• Не пренебрегай здоровьем своего тела;
• Приучайся жить просто и без роскоши.

Лиса Алиса сказала коту Базилио, чтобы найти клад, надо пройти 5 м вперёд, потом повернуть налево и пройти ещё 12 м, а сама побежала напрямик. Кто первый доберётся до клада и на сколько его путь будет короче?

Теоретики.

Значение теоремы Пифагора

Теорема Пифагора – это одна из самых важных теорем геометрии.

Значение состоит ее в том, что с помощью ее можно доказать большинство теорем геометрии.

Знания теоремы и ее приложений позволяет нам применять их при решении задач.

Теорема Пифагора

а

b

b

с

с

а

с

с

а

b

b

а

Доказательство теоремы Пифагора, предложенное древними индусами  

Для первого квадрата:

(a + b) 2 = c 2 + 4S ABC .

Для второго квадрата:

(a + b) 2 = a 2 + b 2 +4S ABC .

Следовательно, c 2 +4S ABC = a 2 +b 2 +4S ABC .

с 2 = a 2 + b 2 .

Древние индусы не записывали доказательство, а свои рисунки сопровождали словом «СМОТРИ»

МЕТОД РАЗЛОЖЕНИЯ Доказательство Эйнштейна

2

1

3

4

С

В

6

7

5

F

8

2

4

O

5

А

м

8

7

6

E

1

3

K

Доказательство из учебника

cos A = AC:AB; cos A = AD:AC

AC : AB = AD : AC; АС 2 = АВ ∙ AD (1)

cos B = BC : AB; cos B = BD : BC.

BC : AB = BD : BC; BС 2 = АВ ∙ BD (2)

АС 2 +ВС 2 = АВ ∙ AD + АВ ∙ BD = AB ∙ (AD + BD) = AB ∙ AB = АВ 2 .

Пифагоровы штаны — шуточное название пифагоровой теоремы, возникающее в силу того, что построенные на сторонах прямоугольного треугольника и расходящиеся в разные стороны квадраты напоминают покрой штанов.

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на его катетах.

Шаржи из учебника XVI века к теореме Пифагора. «Пифагоровы штаны во все стороны равны»

25

Пифагоровы деревья

Пифагоровы деревья

25

Ослиный мост

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga - «бегство убогих» . Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста

Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим - И таким простым путем К результату мы придём.

Высота дерева 8 м, котёнок сидит в 6 м от дерева. Как далеко от котёнка воробей, сидящий на вершине дерева?

Практики. Пифагоровы тройки и способы их формирования

Пифагоровы тройки – это тройки ( x, y, z ) натуральных чисел  x, y, z,  для которых выполняется равенство

n одно из них четное, а другое нечетное, и формируют триаду (m²- n²; 2mn; m²+ n²) " width="640"

Способ 1.

• Обычно пользуются таким приемом подбора решений: произвольные взаимно простые числа m и n , ( m,n )=1, m n одно из них четное, а другое нечетное, и формируют триаду (m²- n²; 2mn; m²+ n²)

Способ 2. Следующий способ возник из наблюдений над некоторыми свойствами триад .

а) Пусть первое число триады (длина одного катета) – нечетное, тогда, например, для триады

(3; 4; 5) наблюдаем: 3 ² =4+5,

(5; 12; 13) наблюдаем: 5² =12+13,

(7; 24; 25) - 7² =24+25 и т. д.

Эти наблюдения показывают приём подбора : взять нечетное число , возвести его в квадрат и результат представить в виде суммы двух последовательных чисел; слагаемые будут вторым и третьим членами триады .

• Пример: триада (13;84;85), 13² = 84+85 действительно 13² + 84² = 85².

б) пусть первое число триады – четное. Тогда, например, для триады (3; 4; 5) наблюдаем: 4 2 =2(3+5), для триады (8;15;17) 8 2 =2(15+17) и т.д. Наблюдения показывают прием подбора:

Взять число, кратное 4, его квадрат разделить на 2 и результат представить как сумму двух последовательных нечетных чисел; слагаемые будут вторым и третьим членами триады.

Пример: ( 16; 63; 65) 16 ²=2(63+65)

Способ 3.

• Из данного пифагорова треугольника со сторонами (а, b, с) можно получить бесконечное множество подобных ему треугольников со сторонами (kа, kb, kс) , где k – произвольное натуральное число.

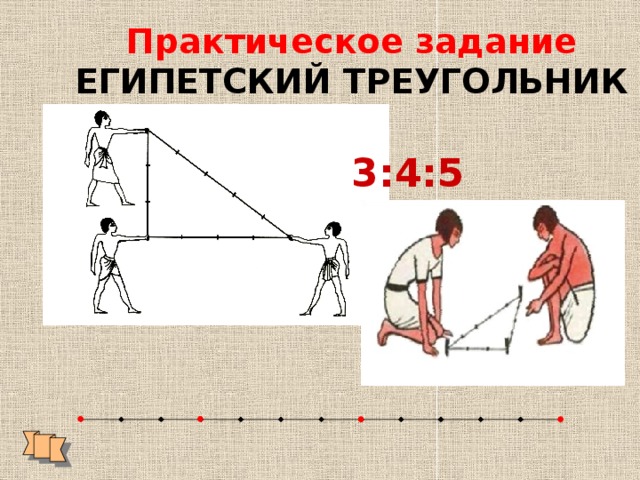
Практическое задание ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК

3:4:5

Длина телескопической удочки 5 м, а длина лески до поплавка 3 м. На каком расстоянии от рыбака находится поплавок?

Самостоятельная работа учащихся.

1.Найдите гипотенузу треугольника по данным катетам a и b.

И) а=6, b=8

Т) а=5, b=6

П) а=2, b=7

Ответ: И)10

Т)

П)

2.Найдите сторону ромба, если его диагонали равны

10см и 24см.

Ответ:13см.

3.Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами:

И)5,6,7

Т)9,12,15

П) 10, 24, 26

Ответ: И) нет; Т) да; П) да.

Домашнее задание.

Оформить в виде доклада 1-3 доказательств теоремы Пифагора,  решить задачу и сделать к ней красивый рисунок, определить, к какой стране относится эта задача.

  Задача .

“ На глубине 12 футов растет

лотос с 13-футовым стеблем.

Определите, на какое

расстояние цветок может

отклониться от вертикали,

проходящей через точку

крепления стебля ко дну”.

И теорема та, что дал нам Пифагор,

Верна теперь, как в день ее рождения .

.

из строк немецкого поэта Альберта фон Шамиссо

«Как хорошо, когда благоденствие человека основано на законах разума».

Будьте благоразумными!

Заполните оценочный лист!

У меня все отлично

У меня все хорошо

Возникли трудности

45

Желаю работать, желаю трудиться,

Желаю успехов сегодня добиться,

Ведь в будущем всё это вам пригодится.

И легче в дальнейшем вам будет учиться.

Литература

1.Акимова С. Занимательная математика Санкт-Петербург.: «Тригон», 1997.

2.Геометрия 7-9: Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, СБ. Кадомцев и др.-12-е изд.-М.: «Просвещение», 2002.

3.Глейзер Г.И. История математики в школе. - М.: «Просвещение», 1981.

4.Еленьский Ш. По следам Пифагора, М., 1961.

5.Журнал «Математика в школе» № 4, 1991.

6. Литцман В. Теорема Пифагора. М., 1960.

7. Скопец З.А. Геометрические миниатюры. М., 1990.

8. Энциклопедический словарь юного математика/ Сост. А.П. Савин.- 3-е изд., испр. и доп. - М.: Педагогика-Пресс, 1997.

9.Энциклопедия для детей. Т.П. Математика /Главный редактор М.Д. Аксенова. - М.: «Аванта+»,1998.

10. Я познаю мир: Детская энциклопедия: Математика. - М., 1997

11.В.К Смышляев О математике и математиках Марийское книжное издательство1977г.

12.Интернет сайты.

13.А.В. Волошинов «Пифагор» М. 1993.

Сигачёв А. А. Пифагор (научно-популярный очерк) // Электронный журнал «Знание. Понимание. Умение». — 2010. — № 6 - История.

14В.Литцман. Теорема Пифагора – государственное издательство физико-математической литературы, Москва, 1960, с.7-16

45

http://www.zaitseva-irina.ru

http://www.samos-travel.com/photos.html

http://images.yandex.ru

http://clck.yandex.ru/redir/AiuY0DBWFJ4ePaEse6rgeAjgs2pI3DW99KUdgowt9Xt0dmymRAsAFBPuMjsGwhcEy

http://ru.wikipedia.org/wiki/Теорема_Пифагора