Применение производной к исследованию функции

Урок №

Тема: «Применение производной к исследованию функций»

Цели:

• Рассмотреть тему: «Применение производной к исследованию функций, к нахождению наибольшего и наименьшего значения функции на отрезке»;

• формирование умения применять теоретические знания к  работе с графиком функции, производной и касательной;

• развитие интереса и внимания при решении задач по готовым чертежам.

Задачи: Формирование навыка работы с производной при решении заданий В8, В11 при подготовке к ЕГЭ

ХОД УРОКА

1. Организационный момент.

Сообщение темы урока и его целей

2. Текущее повторение

Преобразования чис­ло­вых тригонометрических выражений

1. За­да­ние 5 № 26755. Най­ди­те зна­че­ние вы­ра­же­ния .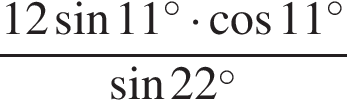

По­яс­не­ние.

Ис­поль­зу­ем фор­му­лу си­ну­са двой­но­го угла  :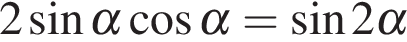

.

Ответ: 6.

2. За­да­ние 5 № 26756. Най­ди­те зна­че­ние вы­ра­же­ния .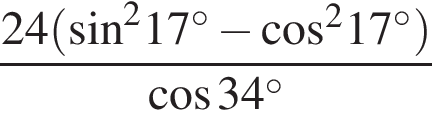

По­яс­не­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

Ответ: -24.

3. За­да­ние 5 № 26757. Най­ди­те зна­че­ние вы­ра­же­ния .

По­яс­не­ние.

Сход­ствен­ные функ­ции до­пол­ни­тель­ных углов равны, по­это­му

.

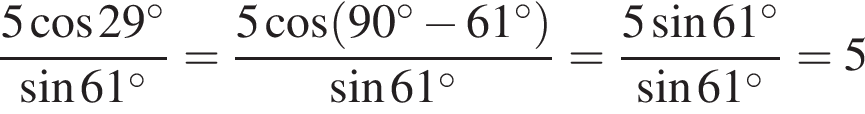Ответ: 5.

4. За­да­ние 5 № 26758. Най­ди­те зна­че­ние вы­ра­же­ния .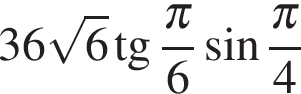

По­яс­не­ние.

Вы­пол­ним пре­об­ра­зо­ва­ния:

.

Ответ: 36.

5. За­да­ние 5 № 26759. Най­ди­те зна­че­ние вы­ра­же­ния .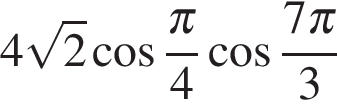

По­яс­не­ние.

В силу пе­ри­о­дич­но­сти ко­си­ну­са

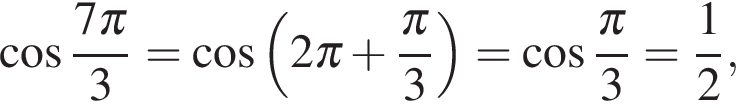
и вы­пол­ним пре­об­ра­зо­ва­ния:

.

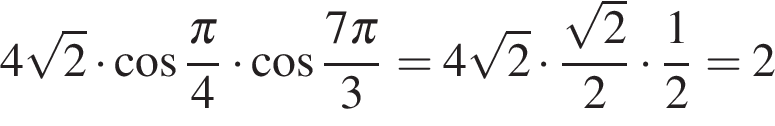Ответ: 2.

1. Изучение новой темы

Исследование функции и ее производной

Исследуйте функцию и постройте её график. слайде 3
Решение задач по готовым чертежам. слайды 4, 5 

4. Нахождение наименьшего и наибольшего значения функции на отрезке

Вспоминаем алгоритм нахождения наибольшего и наименьшего значения функции

слайд 6

Решение типовой задачи  ЕГЭ на нахождение наименьшего и наибольшего значения

слайд 7-8

6. Вычисление значения производной в точке по графику функции и касательной

слайд 10. Учащиеся формулируют, в чём заключается геометрический смысл производной и по чертежу  вычисляют tgA из прямоугольного треугольника АВС. Делаем вывод.
слайд 11
Рассматриваем случай, когда касательная с положительным направлением оси ОХ образует тупой угол. Вспоминаем способы нахождения абсциссы точки касания используя угловой коэффициент касательной. Решение типовой задачи  ЕГЭ В8.

7. Проверочный тест на два варианта

слайд 12

8. Подведение итогов урока

9. Рефлексия слайд 13

10. Домашнее задание слайд 14

Выполнить любое из перечисленных заданий:

• Составить презентацию «Применение производной к исследованию функции»; «Геометрический смысл производной»

• Выполнить тест «Задания ЕГЭ - В8, В11» (приложение1)

• Стр.294 № 230(а); № 232 (в); стр.166 №4

Приложение 1

ТЕСТ

1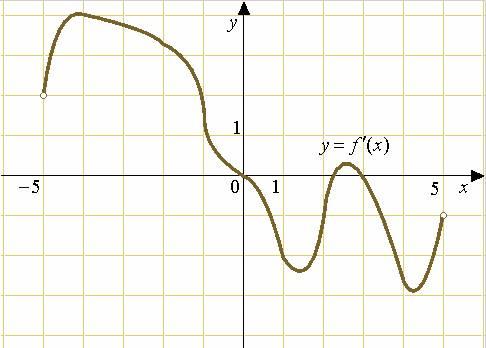. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания.

2. На рисунке изображен график производной функции , определенной на интервале .

• Найдите количество точек экстремума функции на отрезке .

• Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

• Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

3. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции положительна.

4. На рисунке изображен график функции , определенной на интервале 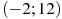. Найдите количество точек, в которых касательная к графику функции параллельна прямой .

5. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка 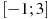принимает наименьшее значение.

6

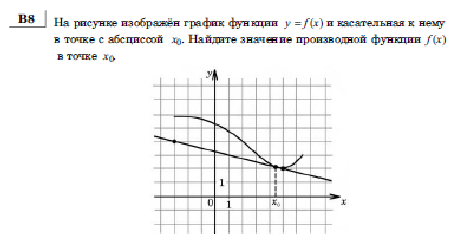
7.

НАЙДИТЕ ПРОИЗВОДНУЮ

1 ответ

1)

2 ответ

2)

3 ответ

3)

4 ответ

4)

5)

5 ответ

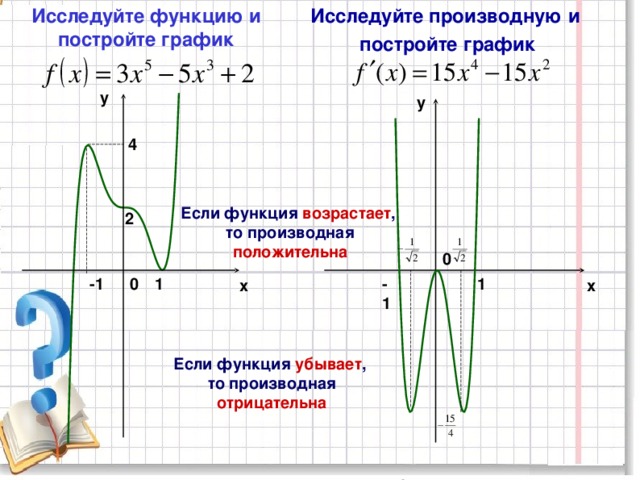
Исследуйте функцию и постройте график

Исследуйте производную и

постройте график

y

y

4

Если функция возрастает ,

то производная

положительна

2

0

1

-1

1

-1

0

x

x

Если функция убывает ,

то производная

отрицательна

Возрастает : (-9;-3) и (3;6)

Убывает : (-3;3)

Максимум : - 3; 6

Минимум ; 3

Находим производную функции

Находим критические точки функции

Если критических точек на

отрезке нет, значит функция

на отрезке монотонна, и

наибольшего и наименьшего

значения функция достигает

на концах отрезка

Если критические точки на отрезке есть, значит нужно вычислить значения функции

во всех критических точках и на концах отрезка, и выбрать

из полученных чисел

наибольшее и наименьшее

1 .

2.

• х = 1 ; х = 5 /3
• f (-1) =18

f(3) = 2

f(1) = 6

f(5/3 ) = 55 / 9

Решение :

ответ

max f ( x ) =f (-1)=18

[-1 ; 3]

min f ( x ) =f ( 3 )= 2

[-1 ; 3]

РЕШЕНИЕ:

Крючки Успокаивает, повышает внимательность, помогает на экзаменах:

1 часть:

1 крючок: сядь, левую щиколотку положи на правую.

2 крючок: вытяни руки вперед, перекрести их, чтобы ладони смотрели друг на друга, сложи руки в замок и снизу подтяни к себе (к груди).

3 крючок: кончиком языка дотронься до твердого нёба.

Сделав 3 крючка, закрой глаза, дыши глубоко и расслабленно, через 20 – 30 секунд снова поставь ноги рядом.

2 часть:

Соедини одноименные пальцы обеих рук подушечками друг с другом домиком или крышей + кончик языка к твёрдому нёбу, подержи 15-30 секунд, дыши глубоко. Закрыв глаза, мысленно представляй перед глазами восьмёрку, по которой движется огонёк любого цвета. Следи закрытыми глазами за движением огонька

y

B

3

1

A

C

-1

1

0

x

2

Геометрический смысл производной:

6 : 8 = 0,75

4 :5 = 0,8

- 0,75

Угол тупой

4

5

II вариант

I вариант

1.

2.

Найдите сумму экстремумов

Найдите сумму экстремумов

2.

3.

Найдите наибольшее и наименьшее значение функции на отрезке

[ 1 / е; 1 ]

[ 1; е ]

«Для меня сегодняшний урок…»

Урок

Я на уроке

1. интересно

Итог

1. работал

2. скучно

2. отдыхал

1. понял материал

3.безразлично

2. узнал больше, чем знал

3.помогал другим

3.не понял

Выполнить любое из перечисленных заданий :

• Составить презентацию «Применение производной к исследованию функции»; «Геометрический смысл производной» Выполнить тест «Задания ЕГЭ - В8, В11» Стр.294 № 230(а); № 232 (в); стр.166 №4
• Составить презентацию «Применение производной к исследованию функции»; «Геометрический смысл производной»
• Выполнить тест «Задания ЕГЭ - В8, В11»
• Стр.294 № 230(а); № 232 (в); стр.166 №4