Проект по теме: Ферма и его великая теорема

Государственное бюджетное профессиональное образовательное учреждение Архангельской области "Котласский транспортный техникум"

/ГБПОУ АО «Котласский транспортный техникум»/

Индивидуальный проект по теме:

Ферма и его великая теорема.

Выполнил: обучающийся 1 курса

группа № 332

Орлов Владимир Владимирович

Проверил: преподаватель математики

Е.Н. Витязева

пос. Вычегодский

2022 год

Содержание:

1. Введение
2. Биография Ферма
3. Интересы Ферма
4. Что же искал Ферма?
5. Великая теорема Ферма
6. Финал истории
7. Заключение
8. Литература

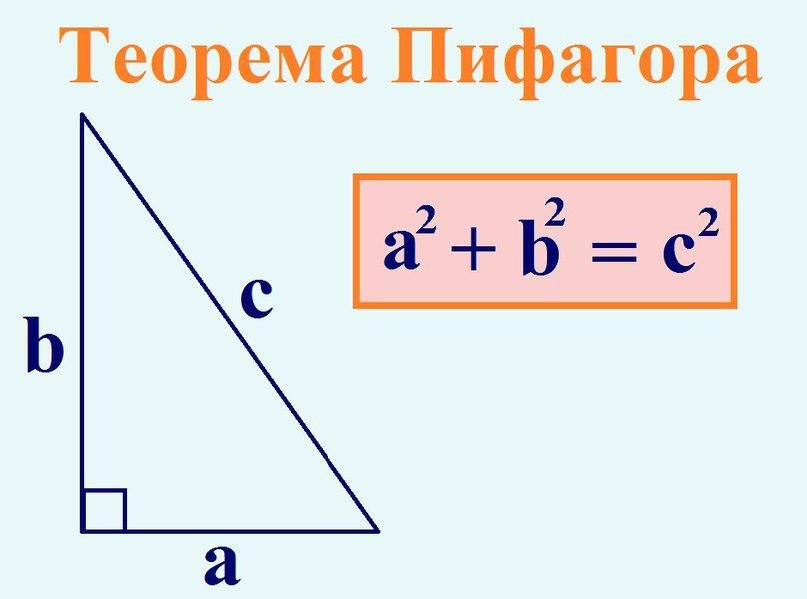
Введение На уроках геометрии мы используем теорему Пифагора. Согласно этой теореме существует множество прямоугольных треугольников, стороны которого соответствуют числам a, b, c данной теоремы. В интернете мне случайно попалась информация о том, что данное равенство при степени больше 2 не имеет целочисленных корней. Я заинтересовался данным вопросом и нашёл информацию о том, что так была сформулирована Великая теорема Ферма, доказать которую математики не могли на протяжении нескольких столетий. Цели и задачи проекта: 1). Изучить литературу по данной теме 2) Отобрать материал для проекта 3) Познакомиться с биографией Пьера Ферма 4) Узнать о математиках, занимающихся теорией чисел 5) Познакомиться с историей доказательства теоремы Ферма 6) Подготовить презентацию для защиты проекта 7) Поддержать развитие интереса у своих сверстников при изучении предмета математика

 

Глава 1. Биография Ферма

Пьер де Ферма

(17.08.1601-12.01.1665)

“Пьер, сын Доминика Ферма, буржуа и второго консулата города Бомона , крещен 20 августа 1601 г. Крестный отец - Пьер Ферма, купец и брат названного Доминика, крестная мать - Жанна Казнюв, и я”. Подпись отсутствует, но предыдущая запись подписана: “Дюма, викарий”. Этот документ искали полтора века и обнаружили лишь в 1846 г. благодаря усилиям адвоката Топиака. До этого считалось, что Ферма родился и умер в Тулузе, где 34 (!) года исправно служил чиновником кассационной палаты Тулузского парламента. Маленький городок Бомон на левом берегу Гаронны вблизи Монтабане-на-Тарне (во Франции более 30 Бомонов) и все его пять тысяч жителей по сей день не в силах осознать значимость находки дотошного адвоката. Здесь родился великий Ферма, последний математик-алхимик, решавший праздные задачи грядущих столетий, тишайший судейский крючок, лукавый сфинкс, замучивший человечество своими загадками, осторожный и благонравный чинуша, подтасовщик, интриган, домосед, завистник один из четырех титанов математики нового времени.

В свой бурный век он прожил основательно и тихо. Он не писал философских трактатов, как Декарт, не был наперсником французских королей, как Виет, не воевал, не путешествовал, не создавал и не посещал математические кружки, не имел учеников и почти не печатался при жизни. Вероятно Ферма, считая себя солидным человеком, стеснялся своей страсти к досужим формальным играм. Не обнаружив никаких сознательных претензий на место в истории, Ферма неожиданно умирает в возрасте 64 лет во время поездки по делам службы.

Его прижизненная известность основана на обильной переписке, в которой он донимал друзей и недругов необычными задачами. Его посмертная слава разрослась благодаря скромным пометкам на полях “Арифметики” Диофанта. Обычно человечеству необходимо несколько десятков лет, чтобы разобраться с наследием очередного неуемного гения. На окончательное осмысление загадок Ферма понадобилось без малого четыре века.

Глава 2.Интересы Ферма.

Интерес к математике обозначился у Ферма как-то неожиданно и в достаточно зрелом возрасте. В 1629 г. в его руки попадает латинский перевод работы Паппа, содержащий краткую сводку результатов Аполлония о свойствах конических сечений. Ферма вдруг задается целью полностью восстановить ход рассуждений знаменитого ученого.

Марен Мерсенн

08.09.1588 – 01.09.1648

(математик, физик, философ, богослов, теоретик музыки)

В 1636 г. он пишет первое письмо Марену Мерсенну: ”Святой отец! Я Вам чрезвычайно признателен за честь, которую Вы мне оказали, подав надежду на то, что мы сможем беседовать письменно; ...Я буду очень рад узнать от Вас о всех новых трактатах и книгах по Математике, которые появилась за последние пять-шесть лет. ...Я нашел также много аналитических методов для различных проблем, как числовых, так и геометрических, для решения которых анализ Виета недостаточен.

Кто такой отец Мерсенн? Это францисканский монах, ученый скромных дарований и замечательный организатор, в течении 30 лет возглавлявший парижский математический кружок, который стал подлинным центром французской науки. В последствии кружок Мерсенна указом Людовика XIV будет преобразован в Парижскую академию наук. Мерсенн неустанно вел огромную переписку, и его келья в монастыре на Королевской площади была своего рода “почтамтом для всех ученых Европы.

Мерсенн счел результаты Ферма достаточно интересными, чтобы ввести провинциала в свой элитный клуб. Ферма тут же завязывает переписку со многими членами кружка и буквально засыпает письмами самого Мерсенна. Кроме того он отсылает на суд ученых мужей законченные рукописи: “Введение к плоским и телесным местам”, а год спустя - “Способ отыскания максимумов и минимумов”. Но идея малости приращения функции вблизи экстремума вовсе не носилась в воздухе. Понадобилось почти столетие, чтобы Жан д’Аламбер в знаменитой “Энциклопедии” признал: “Ферма был изобретателем новых исчислений. Именно у него мы встречаем первое приложение дифференциалов для нахождения касательных”.

Ферма целиком погружается в математику. Его новой страстью становятся числа. Собственно говоря, вся “Теория чисел”, как самостоятельная математическая дисциплина, своим появлением на свет целиком обязана жизни и творчеству Ферма.

В трудах древних, с их культом чертежа, мы находим удивительно мало исследований по теории чисел. Евклид отмечает кое-какие правила делимости и доказывает бесконечность множества простых чисел. Можно также припомнить cribrum Eratosthenis (решето Эратосфена) - метод выделения простых чисел из натурального ряда.

Особняком стоят сочинения Диофанта (III век до н. э.), который рассматривал задачи о представлении чисел и решал неопределенные уравнения в целых числах. Из тринадцати книг его “Арифметики” до наших дней дошло лишь шесть. В Европе переводы сочинений Диофанта на латинский и французский языки появились лишь в начале XVII в. Баше де Мезириак в 1621 г. издал перевод “Арифметики” с собственными подробными комментариями и дополнениями.

Именно это издание, попавшись в руки Ферма, сыграет выдающуюся роль в истории математики.

Бурная история развития идей Ферма только начиналась.

Глава 3. Что же искал Ферма?

Что же искал и что открыл Пьер Ферма, занимаясь числами? Более всего Ферма интересовали способы построения простых чисел. Он мечтал найти явную формулу, которая позволяет быстро вычислять сколь угодно большие простые числа. На полях “Арифметики” он высказал предположение, что таким “генератором” простых чисел будет формула

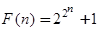, n =0,1,2,...

Действительно, при n = 0, 1, 2, 3, 4 получаем простые числа 3, 5, 17, 257, 65537. Ферма полагал, что при всех прочих n числа F(n) - простые, и неоднократно предлагал своим корреспондентам доказать этот результат .

Понадобилось сто лет, чтобы Леонард Эйлер в 1733 г. опроверг утверждение Ферма.

Итак, Ферма ошибался. Его формула производила в основном составные, а не простые числа. Однако, идея “генерирования” простых чисел была воспринята с энтузиазмом.

Глава 4.Великая теорема Ферма.

На современном это языке звучит так:

не существует отличных от нуля целых чисел x , y и z , для которых имеет место равенство

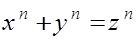
при n 2.

Неопределенные уравнения (т. е. уравнениями с двумя неизвестными) вида 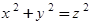интересовали древних греков в связи с теоремой Пифагора. Они искали (и находили) тройки целых чисел, образующие стороны прямоугольного треугольника. Это означает, что при n =1, 2 уравнение в рамке имеет бесчисленное множество решений. Догадка Ферма заключалась в том, что при всех прочих n таких троек не существует.

Вряд ли Ферма был первым, кто пришел к подобному выводу. Например, около тысячи лет назад узбекский математик Хамид ал-Хадженди (что означает Хамид из Ленинабада) утверждал, что уравнение x ³ +y ³ =z ³ не имеет решений в целых числах. Сегодня ясно, что Хамид не имел никаких шансов доказать это утверждение.

На протяжении 20 лет Ферма упорно старается привлечь внимание математиков к “Великой теореме”, предлагая частные случаи в качестве задач. Случай n =3 он формулирует в пяти письмах, причем в последнем письме (от августа 1659 г.) пишет, что доказал теорему для n =3 методом спуска. Между тем “Великую теорему” для общего случая n 2 Ферма сформулировал только один раз в упомянутом замечании на полях “Арифметики”. Он не формулирует ее ни разу ни в одном из писем. Он предлагает только частные случаи (n =3, 4), в отношении которых уверенно говорит, что располагает доказательством. Даже в письме к де Каркави от 1659 г., в котором Ферма перечисляет свои основные достижения, о “Великой теореме” в общем виде нет ни слова. Это может означать только одно: Ферма обнаружил пробелы в своем “поистине удивительном доказательстве”, которые так и не смог устранить.

Разумеется, это не охладило потомков. Начиная с конца XVII в. началась невиданная по своей напряженности гонка за доказательством “Великой теоремы Ферма”. Обманчивая простота формулировки теоремы обрекла тысячи поклонников математики на бесплодные поиски доказательства или опровержения теоремы. Более ста лет никому из ученых не удавалось продвинуться вперед даже при рассмотрении частных случаев конкретных значений показателя n .

Эрнст Эдуард Куммер (29.01.1810-14.05.1893)

В Германии молодой математик Куммер упорно занимается теоремой Ферма. Он пришел к понятию “идеальных чисел”, для которых разложение на простые множители единственно. Обобщение этого понятия привело к созданию головокружительных абстрактных конструкций. Куммер, посвятивший теореме несколько десятков лет, к концу жизни умел доказывать “Великую теорему Ферма” для всех простых показателей n

После Куммера серьезных сдвигов в доказательстве теоремы Ферма не происходило вплоть до 1929 г., когда Вандивер, используя метод Куммера, получил в явном виде некие условия, позволяющие проверять истинность теоремы для любого простого показателя. С этого момента доказательство теоремы для конкретного n свелось к чисто вычислительным проблемам, с которыми легко справляются современные ЭВМ. В результате к концу семидесятых годов нашего столетия “Великая теорема Ферма” была доказана для всех n n , а значит “Великая теорема Ферма” не доказана и не опровергнута.

Глава 5.Финал истории.

Финал этой истории банален. В 1993 г. все ведущие информационные агентства передали сообщение о том, что двум американским математикам удалось доказать теорему Ферма в общем виде. Через полгода в нашей прессе выступил крупнейший алгебраист акад. Фадеев, который подтвердил факт доказательства . XX век покончил с “Великой теоремой Ферма” тихо и буднично. При помощи обычной теории идеалов.

Заключение

В ходе выполнения проекта я:

1). Изучил литературу по данной теме 2) Отобрал материал для проекта 3) Познакомился с биографией Пьера Ферма 4) Узнал о математиках, занимающихся теорией чисел 5) Познакомил с историей доказательства теоремы Ферма 6) Подготовил презентацию для защиты проекта 7) постарался поддержать развитие интереса у своих сверстников при изучении предмета математика

Литература

1. П.Ферма. Исследования по теории чисел и диофантову анализу. М., “Наука”, 1992.

2. М.М.Постников. Теорема Ферма.М., “Наука”, 1978.

3. В.А. Никифоровский, Л.С. Фрейман. Рождение новой математики. М., “Наука”, 1976.

4.Р. Тиле. Леонард Эйлер.Киев, “Вища школа”, 1983.

5. В.Ф. Асмус. Декарт. М., Госполитиздат, 1956.

6. И. Г. Башмакова, Е.И. Славутин. История диофантова анализа от Диофанта до Ферма. М., “Наука”, 1984.

6