Муниципальное бюджетное общеобразовательное учреждение
«Мохченская средняя общеобразовательная школа»
| СОГЛАСОВАНО Заместитель директора по УВР __________ / _______________ / (Подпись) (И.О. Фамилия)
| УТВЕРЖДАЮ Директор __________ /_______________ / (Подпись) (И.О. Фамилия)
Приказ от______________20__г. №____ |
РАБОЧАЯ ПРОГРАММА УЧЕБНОГО ПРЕДМЕТА
| (наименование учебного предмета)
|
| (уровень образования)
|
| (срок реализации программы) |
| Составлена на основе примерной программы |
|
|
|
| (наименование программы, автор программы)
|
|
|
| кем |
|
| (Ф.И.О. учителя или группы учителей, составивших рабочую программу учебного предмета)
|
|
|
|
|
|
|
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ
В результате изучения математики на базовом уровне ученик должен:
Знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений; их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира
Алгебра
Числовые и буквенные выражения
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значение корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, тригонометрические функции, логарифмы.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
У меть:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
Уметь:
находить сумму бесконечно убывающей геометрической прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
Уметь:
решать рациональные, показательные, логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений и неравенств, учитывая ограничения в условии задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем; находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
Уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона ;
вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи).
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Геометрия
Уметь:
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисление длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание обучения
X класс
(6 ч в неделю, всего 216 ч)
Повторение курса 7-9 классов (5 ч)
Числовая функция (7 ч)
Определение числовой функции. Способы ее задания. Свойства функции. Обратная функция и ее график.
Тригонометрическая функция (26 ч)
Числовая окружность. длина дуги единичной окружности. Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Функция y = sin x, ее свойства и график. Функция y = cos x, ее свойства и график. Периодичность функций y = sin x, y = cos x. Построение графика функции y = m f(x) и y = f(kx) по известному графику функции y = f(x). График гармонического колебания. Функции y = tg x и y = ctg x, их свойства и графики.
Введение в стереометрию (7 ч)
Предмет стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом.
Основная цель – сформировать представления учащихся об основных понятиях и аксиомах стереометрии, их использование при решении стандартных задач логического характера, а также об изображениях точек, прямых и плоскостей на проекционном чертеже при различном их взаимном расположении в пространстве.
Параллельность прямых и плоскостей (19 ч )
Параллельность прямых, прямой и плоскости. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Параллельность плоскостей. Тетраэдр и параллелепипед.
Основная цель – дать учащимся систематические сведения о параллельности прямых и плоскостей в пространстве.
При изучении материала темы следует обратить внимание на часто используемый метод доказательства от противного, знакомый учащимся из курса планиметрии.
Здесь учащиеся знакомятся с различными способами изображения пространственных фигур на плоскости.
Тригонометрические уравнения (15 ч)
Первые представления о решении тригонометрических уравнений. Арккосинус. Решение уравнения cos t = a. Арксинус. Решение уравнения sin t = a. Арктангенс и арккотангенс. Решение уравнений tg x = a, ctg x = a.
Простейшие тригонометрические уравнения. Два метода решения тригонометрических уравнений: введение новой переменной и разложение на множители. Однородные тригонометрические уравнения.
Перпендикулярность прямых и плоскостей (20 ч)
Перпендикулярность прямой и плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Двугранный угол. Перпендикулярность плоскостей.
Основная цель – дать учащимся систематические сведения о перпендикулярности прямых и плоскостей в пространстве; ввести понятие углов между прямыми и плоскостями, между плоскостями.
В ходе изучения темы обобщаются и систематизируются знания учащихся о перпендикулярности прямых, перпендикуляре и наклонных, известные им из курса планиметрии. Постоянное обращение к знакомому материалу будет способствовать более глубокому усвоению темы.
Постоянное обращение к теоремам, свойствам и признакам курса планиметрии при решении задач по изучаемой теме не только будет способствовать выработке умения решать стереометрические задачи
данной тематики, но и послужит хорошей пропедевтикой к изучению следующих тем курса.
Преобразование тригонометрических выражений (19 ч)
Синус и косинус суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы. Преобразование выражения A sin x + B cos x к виду C sin (x + t).
Многогранники (12 ч)
Понятие многогранника. Призма. Пирамида. Правильные многогранники.
Основная цель - дать учащимся систематические сведения об основных видах многогранников.
Учащиеся уже знакомы с такими многогранниками, как тетраэдр и параллелепипед. Теперь предстоит расширить представления о многогранниках и их свойствах. В учебнике нет строгого математического определения многогранника, а приводится лишь некоторое описание, так как строгое определение громоздко и трудно не только для понимания учащихся, но и для его применения.
Изучение многогранников нужно вести на наглядной основе, опираясь на объекты природы, предметы окружающей действительности.
Весь теоретический материал темы относится либо к прямым призмам, либо к правильным призмам и правильным пирамидам. Все теоремы доказываются достаточно просто, результаты могут быть записаны формулами, поэтому в теме много задач вычислительного характера, при решении которых отрабатываются умения учащихся пользоваться сведениями из тригонометрии, формулами площадей, решать задачи с использованием таких понятий как «угол между прямой и плоскостью», «двугранный угол» и др.
Производная (38 ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Дифференцирование функции y = f(kx + m).
Уравнение касательной к графику функции y = f(x).
Применение производной для исследования функций на монотонность и экстремумы. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений величин.
Векторы в пространстве (11 ч)
Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.
Основная цель – обобщить изученный в базовой школе материал о векторах на плоскости, дать учащимся систематические сведения о действиях с векторами в пространстве.
Основное внимание следует уделить решению задач, так как при этом учащиеся овладевают векторным методом.
Повторение. Решение задач ( 37 ч)
XI класс
(6 ч в неделю, всего 204 ч)
Повторение курса Х класса (2 ч)
Степени и корни. Степенные функции (20 ч)
Понятие корня n-й степени из действительного числа. Функции у =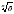 , их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы.
, их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы.
Обобщение понятия о показателе степени. Степенные функции, их свойства и графики.
Метод координат в пространстве (17 ч)
Координаты точки и координаты вектора. Скалярное произведение векторов. Движение.
В ходе изучения темы целесообразно использовать аналогию между рассматриваемыми понятиями на плоскости и в пространстве. Это поможет учащимся более глубоко и осознанно усвоить изучаемый материал, уяснить содержание и место векторного и координатного методов в курсе геометрии.
Показательная и логарифмическая функции (33 ч)
Показательная функция, ее свойства и график. Показательные уравнения. Показательные неравенства.
Понятие логарифма. Функция у = loga x, ее свойства и график. Свойства логарифмов. Логарифмические уравнения. Логарифмические неравенства. Переход к новому основанию логарифма. Дифференцирование показательной и логарифмической функций.
Цилиндр, конус, шар (15 ч).
Цилиндр. Площадь поверхности цилиндра. Конус. Площадь поверхности конуса. Усеченный конус. Сфера. Шар. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.
Изучение круглых тел (цилиндра, конуса, шара) завершает изучение системы основных пространственных геометрических тел.
В ходе знакомства с теоретическим материалом темы значительно развиваются пространственные представления учащихся: круглые тела рассматриваются на примере конкретных геометрических тел, изучается взаимное расположение круглых тел и плоскостей (касательные и секущие плоскости), происходит знакомство с понятиями описанных и вписанных призм и пирамид.
Решается большое количество задач, что позволяет продолжить формирование логических и графических умений.
Первообразная и интеграл (9 ч)
Первообразная. Правила отыскания первообразных. Неопределенный интеграл. Таблица основных неопределенных интегралов.
Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона — Лейбница. Вычисление площадей плоских фигур с помощью определенного интеграла.
Объёмы тел (28 ч)
Объём прямоугольного параллелепипеда. Объёмы прямой призмы и цилиндра. Объёмы наклонной призмы, пирамиды и конуса. Объём шара и площадь сферы. Объёмы шарового сегмента, шарового слоя и шарового сектора.
Учебный материал главы в основном должен усваиваться в процессе решения задач
Элементы математической статистики, комбинаторики и теории вероятностей (15 ч)
Статистическая обработка данных. Простейшие вероятностные задачи. Сочетания и размещения. Формула бинома Ньютона.
Случайные события и их вероятности. Использование комбинаторики для подсчета вероятностей. Произведение событий. Вероятность суммы двух событий. Независимость событий. Независимые повторения испытаний. Теорема Бернулли и статистическая устойчивость. Геометрическая вероятность.
Уравнения и неравенства. Системы уравнений и неравенств (24 ч)
Равносильность уравнений. Общие методы решения уравнений: замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x), разложение на множители, введение новой переменной, функционально-графический метод.
Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями.
Уравнения и неравенства с двумя переменными.
Системы уравнений. Уравнения и неравенства с параметрами.
Обобщающее повторение (41ч)
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
10 класс
| № п/п | Наименование разделов и тем | Всего часов | Из них контрольных работ (зачетов) |
| 1 | Повторение курса алгебры 7-9 классов | 5 | - |
| 2 | Числовые функции | 7 | 1 |
| 3 | Тригонометрические функции | 26 | 2 |
| 4 | Введение в стереометрию | 7 |
|
| 5 | Параллельность прямых и плоскостей | 19 | 2 |
| 6 | Тригонометрические уравнения | 15 | 1 |
| 7 | Перпендикулярность прямых и плоскостей | 20 | 1 |
| 8 | Преобразование тригонометрических выражений | 19 | 1 |
| 9 | Многогранники | 12 | 1 |
| 10 | Производная | 38 | 3 |
| 11 | Векторы в пространстве | 11 | 1 |
| 12 | Повторение курса геометрии | 7 |
|
| 13 | Повторение курса алгебры и начал математического анализа | 30 | 1 |
| Итого: | 216 | 14 |
11 класс
| № п/п | Наименование разделов и тем | Всего часов | Из них контрольных работ (зачетов) |
| 1. | Повторение курса алгебры и начал математического анализа 10 класса | 2 | - |
| 2. | Степени и корни. Степенная функция | 20 | 1 |
| 3. | Метод координат | 17 | 2 |
| 4. | Показательная и логарифмическая функции | 33 | 3 |
| 5. | Цилиндр, конус, шар | 15 | 1 |
| 6. | Первообразная и интеграл | 9 | 1 |
| 7. | Объемы тел | 28 | 2 |
| 8. | Элементы комбинаторики, статистики и теории вероятностей | 15 | 1 |
| 10. | Уравнения и неравенства. Системы уравнений и неравенств | 24 | 1 |
| 11. | Повторение курса математики. | 41 | 1 |
| Итого: | 204 | 13 |





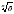 , их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы.
, их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы. 









