Муниципальное бюджетное общеобразовательное учреждение
«Мохченская средняя общеобразовательная школа»
| СОГЛАСОВАНО Заместитель директора по УВР __________ / _______________ / (Подпись) (И.О. Фамилия)
| УТВЕРЖДАЮ Директор __________ /_______________ / (Подпись) (И.О. Фамилия)
Приказ от______________20__г. №____ |
РАБОЧАЯ ПРОГРАММА УЧЕБНОГО ПРЕДМЕТА
| (наименование учебного предмета)
|
| (уровень образования)
|
| (срок реализации программы) |
| Составлена на основе примерной программы |
|
|
|
| (наименование программы, автор программы)
|
|
|
| кем |
|
| (Ф.И.О. учителя или группы учителей, составивших рабочую программу учебного предмета)
|
|
|
|
|
Требования к математической подготовке учащихся .
Учащиеся 5 классов должны иметь представление:
о числе и десятичной системе счисления, о натуральных числах, обыкновенных и десятичных дробях;
об основных изучаемых понятиях (число, фигура, уравнение) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
о достоверных, невозможных и случайных событиях;
о плоских фигурах и их свойствах, а также о простейших пространственных телах.
Учащиеся должны уметь:
выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику;
выполнять арифметические действия с натуральными числами, обыкновенными и десятичными дробями;
выполнять простейшие вычисления с помощью микрокалькулятора;
решать текстовые задачи арифметическим способом; составлять графические и аналитические модели реальных ситуаций;
составлять алгебраические модели реальных ситуаций и выполнять простейшие преобразования буквенных выражений (типа 0,5х +7,2х+8=7,7х+8)
решать уравнения методом отыскания неизвестного компонента действия (простейшие случаи);
строить дерево вариантов в простейших случаях;
использовать геометрический язык для описания предметов окружающего в простейших случаях;
определять длину отрезка, величину угла;
Вычислять периметр и площадь треугольника, прямоугольника, объем куба и прямоугольного параллелепипеда.
Учащиеся 6 класса должны иметь представление:
О числе и числовых системах от натуральных до рациональных чисел;
О вероятности, о благоприятных и неблагоприятных исходах; о подсчете вероятности;
О пропорциональных и обратно пропорциональных величинах.
Учащиеся должны уметь:
Использовать символический язык алгебры, выполнять тождественные преобразования простейших буквенных выражений, применять приобретенные навыки в ходе решения задач;
Решать линейные уравнения, применять данные умения для решения задач;
Решать задачи выделением трех этапов математического моделирования;
Составлять и решать пропорции;
Использовать геометрический язык для описания предметов окружающего мира;
Применять правило произведения при решении простейших вероятностных задач;
Вычислить длину окружности, площадь круга.
Требования к уровню подготовки учащихся (7 класс алгебра)
Данной программой предусмотрено, чтобы в процессе изучения учащиеся овладеют системой математических знаний и умений и будут:
иметь представления о числовых и алгебраических выражениях, о математическом языке и о математической модели, о линейном уравнении как математической модели реальных ситуаций.
знать определение степени с натуральным показателем, свойства степеней.
уметь выполнять действия над степенями с натуральными показателями.
знать определение одночлена, его стандартный вид.
уметь выполнять сложение, вычитание, умножение, возведение одночлена в натуральную степень, деление одночлена на одночлен.
знать определение многочлена, его стандартный вид.
уметь выполнять сложение, вычитание, умножение, деление многочленов.
знать формулы сокращенного умножения.
уметь применять формулы сокращенного умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители, комбинировать различные приемы.
иметь представления об алгебраических дробях.
уметь сокращать алгебраические дроби.
знать основные функциональные понятия и графики функций у=кх+в, у=кх.
уметь строить и читать графики линейной функции, находить наибольшее и наименьшее значения линейной функции на заданном промежутке.
знать определение, свойства, график функции у=х², понятие о непрерывных и разрывных функциях, функциональную символику.
уметь находить наибольшее и наименьшее значения на заданных промежутках, строить и читать графики функции у=х², «кусочных» функций, решать уравнения графическим способом.
знать основные способы решения систем линейных уравнений с двумя переменными: метод подстановки, метод алгебраического сложения, графический метод.
уметь решать системы линейных уравнений с двумя переменными.
уметь применять решение систем линейных уравнений при решении текстовых задач
Требования к уровню подготовки учащихся (7 класс геометрия)
В результате изучения геометрии ученик должен
знать:
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритма;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них , важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования
решать простейшие планиметрические задачи в пространстве;
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин ( используя при необходимости справочники и технические средства);
построений геометрическими инструментами ( линейка, угольник, циркуль, транспортир
В результате изучения алгебры ученик 8 класса должен
значение математической науки для решения задач, возникающих в теории и практике;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа;
выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные выражения рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученные результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
В результате изучения геометрии ученик должен
распознавать геометрические фигуры, различать их взаимное расположение;
выполнять чертежи по условиям задач;
изображать геометрические фигуры; осуществлять преобразования фигур;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения,
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования. Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования несложных практических ситуаций на основе изученных формул и свойств фигур;
вычислений площадей фигур при решении практических задач.
решать следующие жизненно-практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации
В результате изучения математики ученик 9 класса должен уметь :
решать линейные и квадратные неравенства с одной переменной, дробно-рациональные неравенства, неравенства, содержащие модуль;
понимать простейшие понятия теории множеств, задавать множества, производить операции над множествами;
решать системы линейных и квадратных неравенств, системы рациональных неравенств, двойные неравенства;
решать системы уравнений, простые нелинейные системы уравнений двух переменных различными методами;
применять графический метод, метод подстановки, метод алгебраического сложения и метод введения новой переменной при решении практических задач;
составлять математические модели реальных ситуаций и работать с составленной моделью;
исследовать функцию на монотонность, определять наибольшее и наименьшее значение функции, ограниченность, выпуклость, четность, нечетность, область определения и множество значений;
понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств;
описывать свойства изученных функций, строить их графики;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
решать простейшие комбинаторные и вероятностные задачи.
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
использовать приобретенные знания и умения в практической деятельности в повседневной жизни для:
решения несложных практических задач
устной прикидки и оценки результатов вычислений;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений
Содержание
Настоящая программа основного общего образования по математике составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам общего образования, представленных в федеральном государственном образовательном стандарте общего образования, с учетом преемственности с Примерными программами для начального общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Содержание математического образования применительно к основной школе представлено в виде следующих содержательных разделов. Это арифметика; алгебра; функции; вероятность и статистика; геометрия. Наряду с этим в содержание основного общего образования включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения. При этом первая линия — «Логика и множества» — служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — способствует созданию общекультурного, гуманитарного фона изучения курса.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.
Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах.
Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.
Данная программа по математике для основной школы является логическим продолжением программы для начальной школы и вместе с ней составляет описание непрерывного курса математики с 1-го по 9-й класс общеобразовательной школы.
АРИФМЕТИКА
Натуральные числа. Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий.
Степень с натуральным показателем.
Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами.
Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком.
Дроби. Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Проценты; нахождение процентов от величины и величины по ее процентам. Отношение; выражение отношения в процентах. Пропорция; основное свойство пропорции.
Решение текстовых задач арифметическими способами.
Рациональные числа. Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество
рациональных чисел; рациональное число как отношение m/n, где m — целое число, n — натуральное число. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий. Степень с целым показателем.
Действительные числа. Квадратный корень из числа. Корень третьей степени.
Понятие об иррациональном числе. Иррациональность числа √2 и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел.
Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени 10 — в записи числа.
Приближенное значение величины, точность приближения. Округление натуральных чисел и десятичных дробей. Прикидка и оценка результатов вычислений.
АЛГЕБРА
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Степень с натуральным показателем и ее свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Квадратный трехчлен; разложение квадратного трехчлена на множители.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и ее свойства.
Рациональные выражения и их преобразования. Доказательство тождеств.
Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения. Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений.
Линейное уравнение. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к линейным и квадратным. Примеры решения уравнений третьей и четвертой степени. Решение дробно-рациональных уравнений.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах.
Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Примеры решения систем нелинейных уравнений с двумя переменными.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства. Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
ФУНКЦИИ
Основные понятия. Зависимости между величинами. Представление зависимостей формулами. Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, ее график и свойства. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства. Графики функций у =√х, у = 3√x, у = |х|.
Числовые последовательности. Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена.
Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
ВЕРОЯТНОСТЬ И СТАТИСТИКА
Описательная статистика. Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании.
Случайные события и вероятность. Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности.
Комбинаторика. Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал.
ГЕОМЕТРИЯ
Наглядная геометрия. Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Правильные многоугольники. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности.
Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины.
Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира.
Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника и площадь квадрата. Приближенное измерение площадей фигур на клетчатой бумаге. Равновеликие фигуры.
Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры разверток многогранников, цилиндра и конуса.
Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба.
Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.
Геометрические фигуры. Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла.
Параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку.
Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
Треугольник. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника. Сумма углов треугольника. Внешние углы треугольника. Теорема Фалеса. Подобие треугольников. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0 до 180°; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника.
Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции.
Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники.
Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника.
Геометрические преобразования. Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрии, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии.
Решение задач на вычисление, доказательство и построение с использованием свойств изученных фигур.
Измерение геометрических величин. Длина отрезка. Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Периметр многоугольника.
Длина окружности, число π, длина дуги окружности.
Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности.
Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур.
Решение задач на вычисление и доказательство с использованием изученных формул.
Координаты. Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности.
Векторы. Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов.
ЛОГИКА И МНОЖЕСТВА
Теоретико-множественные понятия. Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств.
Иллюстрация отношений между множествами с помощью диаграмм Эйлера — Венна.
Элементы логики. Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример.
Понятие о равносильности, следовании, употребление логических связок: если ..., то в том и только в том случае, логические связки и, или.
Тематическое планирование
5 класс
| № | Наименование разделов | Количество часов | Из них количество часов на практические виды занятий (контрольные, лабораторные, практические работы и т.п.) |
| 1 | Натуральные числа | 46 | 3 |
| 2 | Обыкновенные дроби | 34 | 2 |
| 3 | Геометрические фигуры | 21 | 1 |
| 4 | Десятичные дроби | 43 | 2 |
| 5 | Геометрические теля | 10 | 1 |
| 6 | Введение в вероятность | 4 |
|
| 7 | Повторение | 17 | 1 |
|
| Всего | 175 | 10 |
6 класс
| № | Наименование разделов | Количество часов | Из них количество часов на практические виды занятий (контрольные, лабораторные, практические работы и т.п.) |
| 1 | Положительные и отрицательные числа | 61 | 3 |
| 2 | Преобразование буквенных выражений | 38 | 2 |
| 3 | Преобразование буквенных выражений | 32 | 2 |
| 4 | Преобразование буквенных выражений | 30 | 1 |
| 5 | Преобразование буквенных выражений | 14 | 1 |
|
| Всего | 175 | 9 |
7 класс
| № | Наименование разделов | Количество часов | Из них количество часов на практические виды занятий (контрольные, лабораторные, практические работы и т.п.) |
| 1 | Математический язык. Математическая модель | 14 | 1 |
| 2 | Начальные геометрические сведения | 11 | 1 |
| 3 | Линейная функция | 11 | 1 |
| 4 | Система двух линейных уравнений с двумя переменными | 14 | 1 |
| 5 | Треугольники | 17 | 1 |
| 6 | Степень с натуральным показателем | 7 |
|
| 7 | Одночлены. Операции над одночленами | 9 | 1 |
| 8 | Параллельные прямые | 13 | 1 |
| 9 | Многочлены. Арифметические операции над многочленами | 17 | 1 |
| 10 | Соотношение между сторонами и углами треугольника | 9 |
|
| 11 | Разложение многочлена на множители | 20 | 1 |
| 12 | Прямоугольные треугольники | 11 | 1 |
| 13 | Функция у=х2 | 7 |
|
|
| Итоговое повторение | 15 |
|
|
| Всего | 175 | 10 |
8 класс
| № | Наименование разделов | Количество часов | Из них количество часов на практические виды занятий (контрольные, лабораторные, практические работы и т.п.) |
| 1 | Алгебраические дроби | 21 | 2 |
| 2 | Четырехугольники | 14 | 1 |
| 3 | Функция 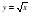 . Свойства квадратичного корня. . Свойства квадратичного корня. | 18 | 1 |
| 4 | Площадь | 14 | 1 |
| 5 | Квадратичная функция. Функция 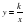 | 18 | 2 |
| 6 | Квадратные уравнения | 22 | 2 |
| 7 | Подобные треугольники | 19 | 2 |
| 8 | Неравенства | 15 | 1 |
| 9 | Окружность | 17 | 1 |
| 10 | Элементы комбинаторики | 4 |
|
| 11 | Повторение | 18 | 1 |
|
| Всего | 180 | 14 |
9 класс
| № | Наименование разделов | Количество часов | Из них количество часов на практические виды занятий (контрольные, лабораторные, практические работы и т.п.) |
|
| Рациональные неравенства и их системы | 13 | 1 |
|
| Рациональные неравенства и их системы | 12 | 1 |
|
| Рациональные неравенства и их системы | 15 | 1 |
|
| Рациональные неравенства и их системы | 8 | 1 |
|
| Рациональные неравенства и их системы | 15 | 1 |
|
| Соотношения между сторонами и углами треугольника. Скалярное произведение векторов | 13 | 1 |
|
| Соотношения между сторонами и углами треугольника. Скалярное произведение векторов | 10 | 1 |
|
| Длина окружности и площадь круга | 16 | 1 |
|
| Прогрессии | 17 | 1 |
|
| Движение | 11 | 1 |
|
| Об аксиомах планиметрии | 2 |
|
|
| События. Вероятность. Статистическая обработка данных | 17 | 1 |
|
| Повторение | 21 |
|
|
| Всего | 170 | 11 |





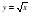 . Свойства квадратичного корня.
. Свойства квадратичного корня.