
Токтогул атындагы №1 мектеп-гимназиясынын математика мугалими Айбекова Акжибек Айбековнанын «Тегиздик. Түз сызык. Шоола. Кесинди» деген темадагы 5 «Г» классына өтүлгөн ачык сабагы 7.12.2017ж.

Сабактын максаты:
- Тегиздик. Түз сызык. Шоола. Кесиндинин узундугу жөнүндө түшүнүк берүү менен билимдери жана билгичтиктери жалпыланат.
- Мисалдардын татаалдыгына жараша туура так чийүү үчүн алган билимдерин колдонууга үйрөнүшөт.
- Ынтымактуулукка, активдүүлүккө, чыгармачылыкка, эмгектенүүгө, топ-топ болуп иштөөгө тарбияланышат.

Топтордун аттары
- Эң чоң жалпы бөлүүчү (ЭЧЖБ)
- Эң кичине жалпы бөлүнүүчү (ЭКЖБ)

Топтордун эрежелери
- Топтун атын жактоо
- Кол көтөрүп сүйлөө
- Айтылган суроолорго туура так жооп берүү
- Сабакка активдүү катышуу

- «Мен байкагычмын»
- Сан 2 ге бөлүнсө алаканыңарды чапкыла
- Сан 3кө бөлүнсө, бутуңарды тыбыраткыла
- Сан 5 кө бөлүнсө класс көргөзгүлө
ЭЧЖБ ЭКЖБ
1. Э киден көп бөлүүчүгө ээ болгон сандар эмне деп аталат?
1. Эки гана бөлүүчүгө ээ болгон сандар эмне деп аталат?
- а) жуп сандар т) курама сандар
- з) так сандар к) жөнөкөй сандар
- д) курама сандар ж) жуп сандар
- з) так сандар т) жөнөкөй сандар
2. 65721 саны кайсыл санга бөлүнөт?
2. Сандардын кайсынысы 4 кө бөлүнөт?
ү) 47516 у) 47597 с) 2846 п) 4778
3) Эгерде сан 2ге да, 3 кө да бөлүнсө, анда ал сан кайсыл санга бөлүнөт?
3. Сандардын ичинен 2ге да, 5 ке да, 10 го бөлүнүүчү сандарды тапкыла?
р) 1565 г)3850 т) 4562 у) 3758
4. Берилген сандардын арасынан 12 ге бөлүнгөн санды тапкыла
р) 2154 о) 20101 н) 5602 и) 41268
4 . Берилген сандардын арасынан 15ге бөлүнгөн санды тапкыла
р) 2155 с) 23205 и) 56025 ң) 40265
5. ЭЧЖБ (32; 16) =
ы) 16 н) 8 о) 4 п) 32
6. ЭКЖБ (9: 27) =
з) 27 д) 9 в) 36 г)54
7 . Эң кичинекей жөнөкөй сан
л)50 б) 1 ү) 24 ы) 2
8. Экиге бөлүнбөгөн сандарды ...........деп атайбыз
д) курама сандар ж) жуп сандар
к) так сандар к) жөнөкөй сандар
А) 48, з) 24 в) 36 г) 12
6. ЭЧЖБ (48;36) =
А) 2 б) 48 д ) 12 у) 6
7. Жөнөкөй сандардын ичинде бир жуп сан бар, ал кайсы сан
и) 2 б) 8 у) 10 г) 20
8. Экиге бөлүнгөн сандарды ...........деп атайбыз
- д) курама сандар к) жуп сандар
- ү) так сандар к) жөнөкөй сандар


Тегиздик деп эмненин элесететсиңер?

- Тегиздикке алып келүүчү мисалдар, столдун, класстык досканын, терезенин айнегин, тынч турган суунун беттерин тегизик катары элестетүүгө болот. Бирок тегиздиктин чеги жок.


№ 256
Дептериңерге М чекити белгилегиле. Сызгычт пайдаланып ал чекит аркылуу өткөн түз сызык жүргүзгүлө. М чекити аркылуу дагы бшк түз сызык жүргүзүүгө болобу? Канчаны?
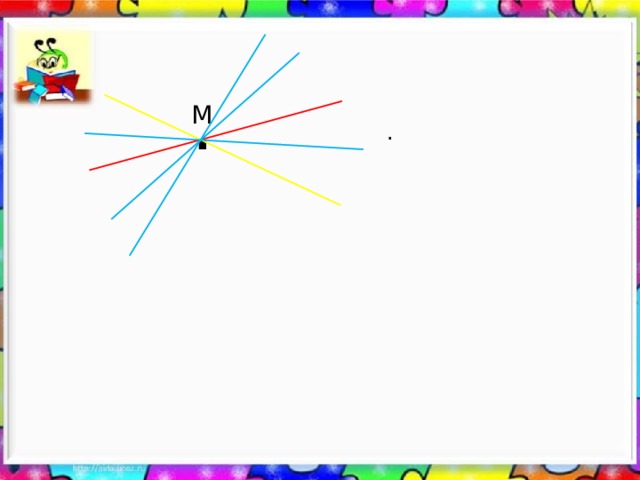
.
М
.

№ 257
Дептериңерге А жана В чекиттерин белгилегиле. Алар аркылуу өтүүчү түзсызыкты сызгыч менен жүргүзгүлө. Ушул эки чекит аркылуу өтүүчү дагы бир түз сызык жүргүзгүлө. Эмнени байкадыңар?
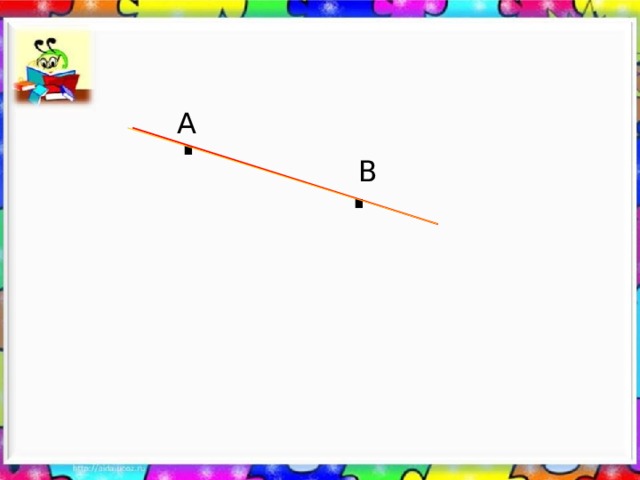
.
A
.
B

- Тегиздикте берилген бир чекит аркылуу чексиз көп түз сызыктарды, эки чекит аркылуу бир гана түз сызык жүргүзүүгө болот

- Түз сызык чексиз көп чекиттерден турат. Ошондуктан түз сызыктан каалагандай чекитти белгилеп алууга болот. Ошол чекит аны тең экиге бөлөт. Алардын ар бири шоола деп аталат. Ар бир шоола бир жагына чектелет, экинчи жагын карай чексиз созулат. Ал эми бөлүүчү чекит шооланын башталышы деп аталат
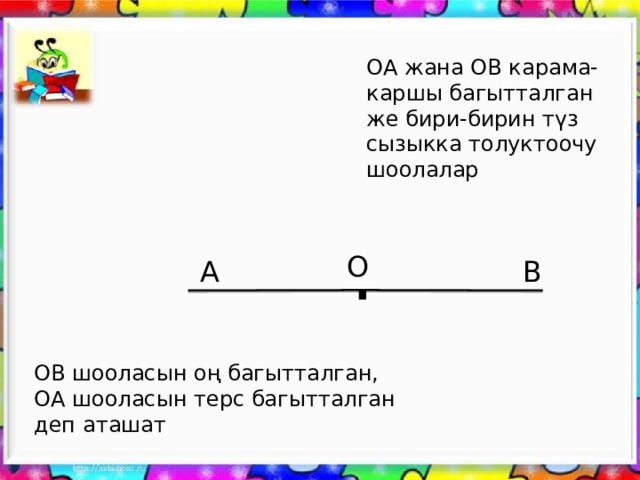
ОА жана ОВ карама-каршы багытталган же бири-бирин түз сызыкка толуктоочу шоолалар
.
О
А
В
ОВ шооласын оң багытталган,
ОА шооласын терс багытталган деп аташат

№ 259
Тегиздикте жатуучу бир нече фигураларды сызгыла жана аларды атап бергиле
.
B
.
A
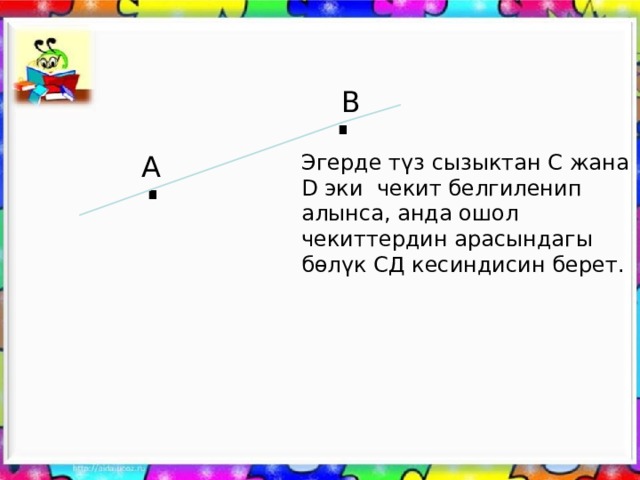
Эгерде түз сызыктан С жана D эки чекит белгиленип алынса, анда ошол чекиттердин арасындагы бөлүк СД кесиндисин берет.

АВ жана С D кесиндилери берилген. АВ кесиндисин С D кесиндиси менен ченегиле. С D кесиндисин А дан баштапудаалаш коюп чыгабыз. Канча жолу коюлду?

- АВ=3*С D
- Мындай учурда С D бирдик кесинди деп аталат.
- Демек, кесиндинин узундугун ченөө дегенибизал кесиндиде канча бирдик кесинди бар экендигин көрсөтүүчү санды табуу болуп эсептелет.

Бизге ка й сы фигуралар тааныш?
- Түз сызык, шоола, кесинди, тик бурчтук,квадрат, айлана,тегерек,бурч, көп бурчтук тегиздикке каралат, анткени аталган фигуралар толугу менен тегиздикте жатат. Аларды жалпысынан жалпак фигуралар деп коюшат.

- Ал эми куб, призма,цилиндр, шар ж.б. фигуралар толугу менен тегиздикте жатышпайт. Аларды көлөмдүү фигуралар дейбиз.

№ 262
10-сүрөттө бир тегиздикте жатуучу А,В,С үч чекити берилген. Ар бир эки чекит аркылүү өтүүчү түз сызыктарды сызгыла. Алардын ар бирин белгилегиле. С чекити кайсы түз сызыкта жатат (жатпайт)?
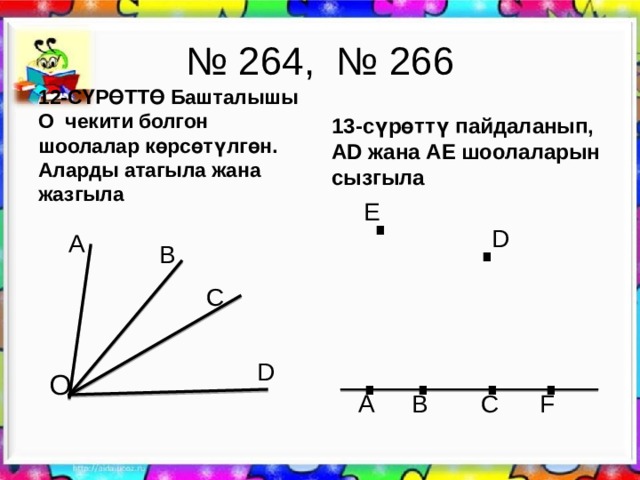
№ 264, № 266
13-сүрөттү пайдаланып, AD жана AE шоолаларын сызгыла
12-СҮРӨТТӨ Башталышы О чекити болгон шоолалар көрсөтүлгөн. Аларды атагыла жана жазгыла
.
.
E
D
А
В
С
.
.
.
.
D
О
А
В
С
F

D
О
Е
В
А
С
А
№ 267, №268
13-сүрөттү пайдаланып, AD жана AE шоолаларын сызгыла
АЕ шооласына карама-каршы шооланы сызгыла (15-сүрөт)
Аны атагыла жана белгилегиле
.
.
М
С
В
А
С
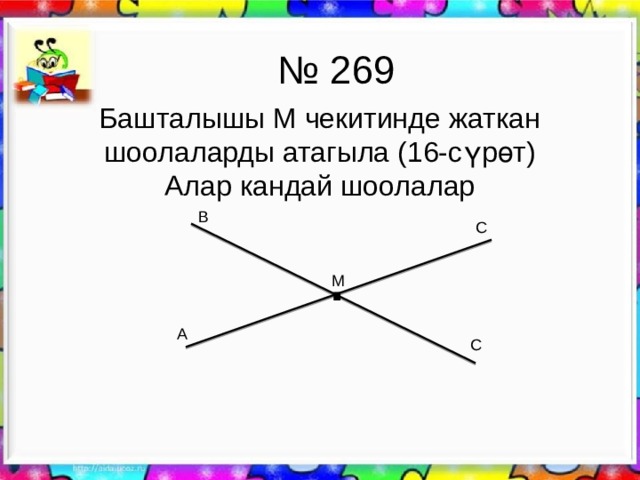
№ 269
Башталышы М чекитинде жаткан шоолаларды атагыла (16-сүрөт) Алар кандай шоолалар
.

Эсептегиле
- АВ кесиндиси жана анда жатуучу С чекити берилген. АВ=7 см, АС= 4 см 5 мм болсо, СВ кесиндисинин узундугун тапкыла.
АВ жана СВ кесиндилерин салыштыргыла.

Табышмак
- Башы бар, аягы жок
- Айнектин бети
- Башыда бар, аягыда бар
- Башы жок, аягы жок
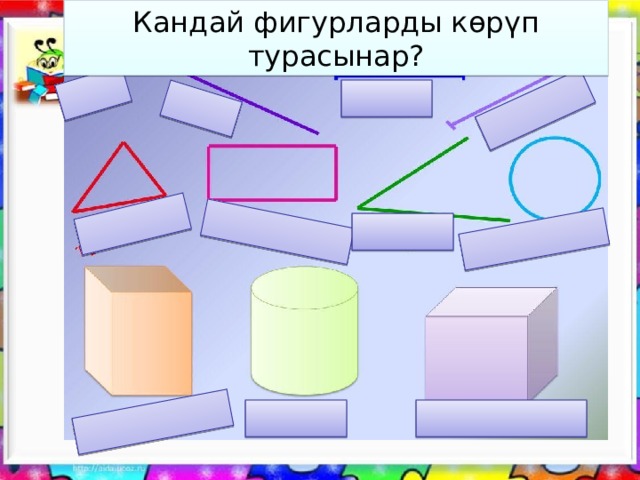
Кандай фигурларды көрүп турасынар?
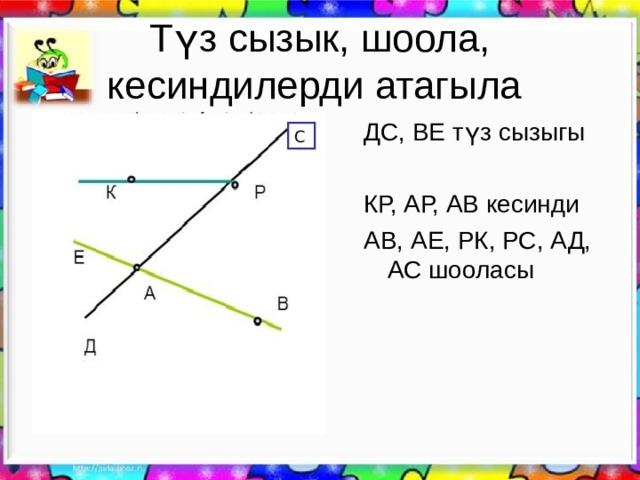
Түз сызык, шоола, кесиндилерди атагыла
ДС, ВЕ түз сызыгы
КР, АР, АВ кесинди
АВ, АЕ, РК, РС, АД, АС шооласы
С

ДС, ВЕ түз сызыгы
КР, АР, АВ кесинди
АВ, АЕ, РК, РС, АД, АС шооласы


Тапшырма
1. Эки чекит аркылуу а түз сызыгын жүргүзгүлө
3. АВ жана ОЕ кесиндисин сызгыла .
5. Канча кесиндини көрүп турасың?
.
.
.
А
В
С



















































