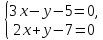Технологическая карта урока "Метод подстановки",7 класс

ФИО учителя

Романова Евгения Ильинична

должность

заместитель директора школы по УР, учитель физики и математики (по совместительству)

Наименование ОУ

МБОУ «Санномыская средняя общеобразовательная школа»

место нахождения ОУ (адрес)

671419, Республика Бурятия, Хоринский район, с. Санномыск, улица Ленина, 1.

Предмет:

алгебра

Класс:

7

УМК

Учебник. Алгебра. 7 класс: учеб. для общеобразовательных учреждений /А.Г. Мордкович и др; под ред. А.Г. Мордковича -М.: Мнемозина, 2014г., часть I и II.

Глава №:

3, & 12

Тема урока:

«Решение системы линейных уравнений с двумя переменными методом подстановки»

Вид урока:

урок смешанный

Тип урока:

изучение нового материала

Форма урока:

урок открытых мыслей

Цель урока:

Формирование у учащихся умения решать системы двух линейных уравнений с двумя переменными методом подстановки.

Цели познавательной деятельности:

практическое применение.

Репродуктивная познавательная деятельность (Р) основана на запоминании информации о знаниях и способах деятельности, предъявленной ученику в ходе обучения.

Р: знать, алгоритм решения системы двух линейных уравнений с двумя переменными методом подстановки.

Частично-поисковая учебная деятельность (Ч-П) поиск скрытой, требующей перестройки информации в ситуациях, несколько измененных по сравнению с рассматриваемыми в учебном процессе, конкретизация обобщенных описаний деятельности, осмысление и поиск вариантов в выполнении учебных заданий.

Ч-П: доказать, что одну и ту же систему двух линейных уравнений с двумя переменными можно решить не только графическим методом, но и методом подстановки.

Проектировочно-конструкторская деятельность (П-К) проявляется в познавательной активности ученика, в его

способности осознать цели и разработать план их достижения, это процесс решения одной и той же системы двух линейных уравнений графическим методом и методом подстановки требующий самостоятельного переконструирования и расширения своей системы знаний, через работу с учебником.

П-К: самостоятельно составить алгоритм решения системы линейного уравнения с двумя переменными, используя метод подстановки; провести сравнение между графическим методом решения системы линейных уравнений с двумя переменными с методом подстановки и выяснить какой метод более эффективен и почему.

Задачи урока:

образовательная

Сформировать алгоритм решения системы двух линейных уравнений с двумя переменными, на основе использования метода подстановки

в результате исследовательской деятельности научить учащихся применять данный алгоритм при решении системы двух линейных уравнений с двумя переменными.

воспитательная

Воспитывать культуру взаимодействия в группах; формировать добросовестное отношение к учебному труду, положительной мотивации к учению, коммуникативных умений, способствовать воспитанию гуманности, дисциплинированности, эстетического восприятия мира.

развивающая

содействовать развитию речи, мышления, познавательных умений; содействовать овладению методами научного исследования: анализа и синтеза, развивать интерес к предмету «алгебра», через исследовательскую деятельность при решении системы линейных уравнений различными методами, умения работать с учебной литературой.

Решаемые проблемы:

отсутствие знаний о решении системы двух линейных уравнений методом подстановки.

Методы урока: 

проблемный, частично-поисковый, объяснительно-иллюстративный, эвристический, репродуктивный.

Методические приёмы:

интонационное выделение учителем логически важных моментов изложения; выделение цветным мелом; демонстрация графиков, сравнение решения системы двух линейных уравнений графическим методом и методом подстановки, с целью иллюстрирования  определённых выводов. 

Метапредметные связи:

Связь с физикой – вывод формул с помощью метода подстановки.

Оборудование:

мел; координатная плоскость, линейка, карточки, презентация.

Планируемые результаты /в соответствии с ФГОС/

-знать алгоритм решения системы двух линейных уравнений методом подстановки.

-уметь решать и использовать для решения системы «Алгоритм решения системы двух уравнений с двумя переменными методом подстановки»

Достигаемые результаты /в соответствии с ФГОС/

понятия

Предметные результаты

Метапредметные результаты

Личностные результаты

подстановка,

алгоритм

Овладение алгоритмом решения системы двух уравнений с двумя переменными методом подстановки

Знать последовательность шагов, то есть алгоритм.

Уметь выражать у через х из первого уравнения системы, подставлять полученное на первом шаге выражение вместо у во второе уравнение системы, решать полученное на втором шагу уравнение относительно х, подставлять найденное на третьем шаге значение х в выражение у через х, полученное на первом шаге, записывать ответ в виде пары значений (х; у), которые были найдены соответственно на третьем и четвёртом шагах.

Кратко и точно отвечать на вопросы

Познавательные УУД: работа с разными типами информации, с учебными моделями, установление причинно-следственных связей

Личностные УУД:

убежденность в возможности познания метода подстановки и умения применять данный метод для решения системы уравнений с двумя переменными.

Регулятивные УУД:

Построение индивидуальной стратегии освоения алгоритма решения системы двух уравнений с двумя переменными методом подстановки.

Коммуникативные УУД:

речевая деятельность, навыки сотрудничества и ведения диалога.

Осознание важности изучения алгоритма решения системы двух уравнений с двумя переменными методом подстановки;

формирование познавательного интереса к точным наукам.

Технологии:

личностно-ориентированного обучения, проблемное обучение, ИКТ, индивидуального обучения, здоровьесберегающая технология.

Контроль:

промежуточный – для оценки уровня сформированности ЗУН, по окончанию этапа изучения материала и выяснения необходимости его корректировки

Форма контроля:

 Индивидуальная работа с карточками, работа в парах, оценивание работы учениками.

Домашнее задание:

Учебник «Алгебра», часть I, стр.64 &12, выучить алгоритм решения системы двух уравнений с двумя переменными методом подстановки; Учебник «Алгебра», часть II, стр.66 № 12.2 (а, б) решить систему уравнений методом подстановки и графически, знать «+» и

«-» данных методов решения.

Формы работы:

Индивидуальная работа

Работа в парах и группах

Фронтальная (коллективная) работа

Ресурсы:

Цифровые ресурсы: наглядные мультимедийные пособия http://klass_matematika.narod.ru

Учебно-методическая литература:

http://mon.gov.ru ФГОС на сайте Министерства образования и науки РФ, http:// standart.edu.ru

Средства ИКТ: компьютер, принтер.

Планирование учебной деятельности

Этапы учебной занятости

Деятельность учителя

Деятельность ученика

1.Организационный этап

Дидактическая задача: создание комфортной образовательной среды.

Приветствие. Создание положительного эмоционального настроя учащихся.

Готовность рабочего места.

Личностные: мотивировать свои действия; готовность к восприятию; проявлять внимательность; желание больше узнать.

Результат сотрудничества: создание благоприятной обстановки.

2.Мотивационный этап

Дидактическая задача: проверка уровня знаний имеющихся у учеников, имеющих взаимосвязь с изучением новой учебно-познавательной деятельностью.

Создается проблемная ситуация: решите систему уравнений графическим способом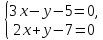

Вопрос: чему конкретно равны абсцисса и ордината точки А?

Вопрос: можно ли данную систему решить иным способом?

решает систему методом подстановки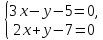

что я использовала при решении системы уравнений?

определите ключевое действие.

попробуйте сформулировать тему урока.

обобщает высказанные учащимися версии и формулирует тему урока: «Решение системы линейных уравнений с двумя переменными методом подстановки»

учащиеся индивидуально решают систему уравнений (один учащийся решает на доске). Выполняют сверку полученных ответов и оценивают каждый себя по критерию:

1) выразил «у» через «х» в первом уравнении – 1 балл;

2) выразил «у» через «х» во втором уравнении – 1 балл;

3) построил таблицу для первого значения «у» - 1 балл;

4) построил таблицу для второго значения «у» - 1 балл;

5) построил координатную плоскость и графики линейных функций – 3 балла;

6) нашёл точку пересечения графиков А, а значит – единственное решение заданной системы – 1 балл;

7) правильно записал ответ – 1 балл.

«5» - допущена 1 ошибка;

«4» - допущено две ошибки;

«3» - допущено 3 ошибки;

«2» - допущено больше 3 ошибок.

Правильное решение системы смотри на слайде.

Точно определить нельзя, так как точка А как бы «висит» внутри определённой клеточки.

Версии ответов.

вы подставили полученное на первом шаге выражение вместо «у» во второе уравнение системы.

подстановка.

учащиеся высказывают свои версии

Коммуникативные: компетентность и учет позиции других учеников

Регулятивные: оценка - оценивание качества и уровня имеющихся первоначальных знаний

Результат сотрудничества: объективность при оценивании первоначальных знаний

Деятельностный этап связанный с мотивацией

Дидактическая задача: обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности

3.Этап изучение нового материала

деятельностный этап -получения новых знаний

Дидактическая задача: открытие нового знания – поиск решения проблемы – выражение решения проблемы

Откройте свои рабочие тетради запишите дату, классная работа и тему сегодняшнего урока

- Какую бы вы поставили цель работы на этом уроке?

Обобщение учителем версий выдвинутых учениками по цели урока

Цель, которую мы ставим сегодня перед собой: научиться решать систему линейных уравнений с двумя переменными методом подстановки, используя «Алгоритм решения системы двух уравнений с двумя переменными методом подстановки».

класс разбивается на 3 группы.

Задание. Составьте алгоритм для решения системы линейных уравнений с двумя переменными, применяя метод подстановки пошагово.

Изучите алгоритм решения систем уравнений с двумя переменными методом подстановки. (стр. 65, учебник «Алгебра», часть I ). Сверьте со своим алгоритмом, внесите изменения при необходимости.

На основании полученного алгоритма выполните задания.

Задание 1.

Решите систему уравнений, используя данный алгоритм:

1. Выразите с первого уравнения переменную у через х и подставим полученное выражение в другое уравнение системы:

2.Решим полученное уравнение с одной переменной:

3.Находим соответствующее значение второй переменной.

Ответ: (4;2).

- Какой из методов решения линейных уравнений (графический или метод подстановки) наиболее удобен и почему? Назовите «+» и «-« обеих методов.

Записывают дату урока, классная работа и тему урока в тетрадь

Опираясь на поставленную тему урока ставят цель урока.

пробуют составить алгоритм.(работа в группах). Один учащийся из группы оглашает составленный алгоритм, остальные дополняют, исправляют, добиваясь правильного результата.

Регулятивные: целеполагание;

Коммуникативные: умения слушать и вступать в диалог;

Познавательные: универсальные логические действия;

Личностные: проявлять понимание и уважение к науке; толерантные отношения.

работают с учебником. При необходимости вносят изменения или дополнения.

Графический метод не всегда даёт точное решение, но с его помощью можно сделать следующие выводы:

- графиками обеих систем уравнений являются прямые;

- эти прямые могут пересекаться, причём только в одной точке, а это значит, что система имеет единственное решение;

- прямые могут быть параллельны, а это значит, что система не имеет решения;

- эти прямые могут совпасть, а это значит, что система имеет бесконечно много решений.

Метод подстановки не всегда эффективен (то есть не всегда быстро приводит к цели), но зато наиболее надёжный, так как всегда приведёт к желаемому результату.

Физкультминутка

Способы организации переключения внимания учащихся

Мы поставили пластинку

Начинаем все разминку

Головой покрутим резво, 
Вправо-влево, вправо-влево. 
(повороты в сторону головой.) 

Так мы лучше думать будем. 
В круговую поворот и поворот, 
А потом наоборот. 
(Вращения головой в круговую.) 

Влево плечи разверни. 
А теперь направо. Ну-ка! 
Упражненье повтори. 
(Вращение туловищем в стороны.) 

Пальцы в кулачки зажми, разожми и три раза повтори

(сжимают и разжимают кулачки)

А теперь на спинку стула ты откинься

в тишину на минуту погрузись

Ученики выполняют под спокойную музыку упражнения на расслабление мышц шеи, плеч, позвоночника, кисти рук повторяя за учителем.

Личностные: проявляют понимание необходимости заботе о своем здоровье.

4. Этап обобщения и закрепления нового материала.

Дидактическая задача: обеспечение усвоения новых знаний и способов действий на уровне применения в изменённой ситуации.

Самостоятельное, творческое использование сформированных умений и навыков

Динамическая задача: формирование целостной системы ведущих знаний по теме.

5. Заключительный этап.

Дидактическая задача: дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы

6. Рефлексия.

Дидактическая задача: мобилизация учащихся на рефлексию своего поведения (мотивации, способов деятельности, общения); усвоение принципов саморегуляции и сотрудничества

7. Домашнее задание.

Дидактическая задача: провести инструктаж по выполнению д/задания

Итак, вы теперь знаете «Алгоритм решения системы уравнений с двумя переменными методом подстановки». Глядя на свой опорный конспект в тетради и на Алгоритм, постарайтесь применить полученные на сегодняшнем уроке знания, для выполнения следующих заданий:

Задание 1. Заполните пустые клетки и решите систему уравнений:

Ответ: (1;-2)

Задание 2. Учебник «Алгебра», часть II, стр. 66 № 12.4 (а, в)

Итак, наш урок подходит к завершению. Вы сегодня неплохо поработали. Решали самостоятельно поставленные перед вами проблемы. Делали правильные выводы.

Решать можно вечно. Ведь математика бесконечна.

Вспомните цель урока.

Достигли ли вы цели урока? В какой степени?

Почувствовали ли себя сегодня на уроке настоящими математиками? Почему?

Спасибо всем нам за урок,

А главное, чтоб был он впрок!

Я надеюсь, что полученные вами знания о решении системы линейных уравнений с двумя переменными методом подстановки вы будете использовать не только на уроках по различным предметам, но и будете применять их в повседневной жизни.

- Что вам понравилось на сегодняшнем уроке?

- Что не понравилось?

А теперь давайте выставим оценки.

Предлагает оценить урок и свою деятельность, используя жетоны разного цвета: красный +; желтый +-; синий

Учебник «Алгебра», часть I, стр.64 &12, выучить алгоритм решения системы двух уравнений с двумя переменными методом подстановки; Учебник «Алгебра», часть II, стр.66 № 12.2 (а, б) решить систему уравнений методом подстановки и графически, знать «+» и

«-» данных методов решения.

Работают индивидуально по карточкам.

Взаимопроверка. Правильное решение на слайде.

работа в парах, коллективная работа. Проверьте решение по слайду.

Регулятивные: коррекция и оценка ситуации; умения прогнозировать; соотносить план и совершенные операции по ходу работы с заданиями

Коммуникативные: приводить убедительные доказательства; удерживать логику повествования; учитывать позицию собеседника.

Познавательные: преобразовывать модели в соответствии с содержанием учебного материала и поставленной учебной задачи; структурирование знаний

Личностные: проявлять терпение, доброжелательность к собеседнику; сравнивать различные точки зрения;

Результат сотрудничества: сравнивают и анализируют полученные результаты; приводят

примеры практического использования данной темы, устанавливая связь с другими науками (физика)

Высказывают свою точку зрения

Регулятивные: осознание себя как частицу мира математики.

Коммуникативные: составление небольших монологических высказывании; приводят убедительных доказательства;

Познавательные: воспроизведение по памяти информации; сравнительный анализ решения системы линейных уравнений графическим методом и методом подстановки;

Личностные: выражает положительное отношение к процессу познания

Результат сотрудничества: анализ своей деятельности

Ученики оценивают работу своих товарищей, работу свою, работу группы

Личностные: способность к самооценке на основе критерия успешности учебной деятельности; идентифицировать себя с принадлежностью класса для решения учебной задачи.

Регулятивные: уметь оценить правильность выполнения действия

Результат сотрудничества: самоанализ урока

Ученики записывают, задают вопросы

Познавательные: поиск необходимой информации