| Организует изучение учебного материала по учебнику Учащиеся уже встречались с решением неполных квадратных уравнений. Поэтому основная цель состоит в систематизации их знаний, ознакомлении с новым понятием и овладением конкретными приемами решения неполных квадратных уравнений. Объяснение нового материала проводится в несколько этапов и предполагает большую долю самостоятельности учащихся. 1. Введение понятия неполного квадратного уравнения. Учащиеся могут сами подойти к изучаемому понятию, если предложить им выполнить соответствующее задание. Задание. Назовите коэффициенты квадратных уравнений. Что общего можно найти во всех этих квадратных уравнениях? а) 3x – 5x2 = 0; г) 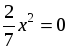 ; ; б) 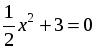 ; д) 6x2 – 4 = 0; ; д) 6x2 – 4 = 0; в) 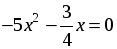 ; е) x2 – x = 0. ; е) x2 – x = 0. Учащиеся должны заметить, что во всех рассматриваемых уравнениях хотя бы один коэффициент равен нулю. Учитель сообщает, что такие квадратные уравнения называются неполными, и просит учащихся сформулировать соответствующее определение. Определение. Квадратное уравнение называют неполным, если хотя бы один из коэффициентов b или c равен нулю. 2. Виды неполных квадратных уравнений. Предложить учащимся выделить и записать все виды неполных квадратных уравнений. 1) ax2 + c = 0, где с ≠ 0; 2) ax2 + bx = 0, где b ≠ 0; 3) ax2 = 0. 3. Решение неполных квадратных уравнений различных видов. Необходимо, чтобы учащиеся при помощи учителя рассмотрели решение каждого из видов неполных квадратных уравнений, сделали выводы и записали решение в общем виде. 1) Неполные квадратные уравнения вида ax2 + c = 0, где с ≠ 0. Начать можно с решения конкретных уравнений данного вида: а) 64x2 – 49 = 0; б) –2x2 + 8 = 0; в) 16x2 + 1 = 0. Затем учащиеся без труда смогут сформулировать алгоритм решения неполных квадратных уравнений этого вида. Алгоритм. Для решения неполного квадратного уравнения вида
ax2 + c = 0 при с ≠ 0 переносят его свободный член в первую часть и делят обе части уравнения на а. В результате получается следующее уравнение: 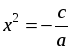 , равносильное уравнению ax2 + c = 0. , равносильное уравнению ax2 + c = 0. Далее следует обратить внимание на количество корней полученного уравнения 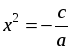 . Учащиеся понимают, что такое уравнение либо не имеет корней, либо имеет два корня, которые являются противоположными числами. . Учащиеся понимают, что такое уравнение либо не имеет корней, либо имеет два корня, которые являются противоположными числами. В классе с высоким уровнем подготовки можно привести доказательство этого уравнения. Доказательство. Если в уравнении 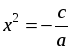 числа а и с одного знака, то числа а и с одного знака, то 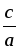 0, тогда – 0, тогда –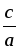 а и с разных знаков, то а и с разных знаков, то 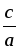 0. В этом случае уравнение имеет два корня: 0. В этом случае уравнение имеет два корня: 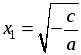 и и 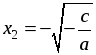 . Эти корни – противоположные числа. . Эти корни – противоположные числа. 2) Неполные квадратные уравнения вида ax2 + bx = 0, где b ≠ 0. Как и при рассмотрении первого вида неполных квадратных уравнений, начать нужно с решения конкретных уравнений: а) 10x2 + 9x = 0; б) –2x2 + 5x = 0. Затем формулируется алгоритм решения таких уравнений. Алгоритм. Для решения неполного квадратного уравнения вида ax2 + bx = 0 при b ≠ 0 его левую часть раскладывают на множители и получают уравнение: x(ax + b) = 0. Произведение x(ax + b) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, то есть х = 0 или ax + b = 0; 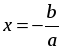 . . Таким образом, неполное квадратное уравнение вида ax2 + bx = 0 при b ≠ 0 всегда имеет два корня: 0 и 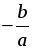 . . 3) Неполные квадратные уравнения вида ax2 = 0. Если не рассматривать этот вид неполных квадратных уравнений, то появляется опасность возникновения очень распространенных ошибок у учащихся. Решая, например, уравнение 4x2 = 0, они получают: x2 = 4 или x = 4 и прочее. Поэтому необходимо этот вид уравнений выделить отдельно и сделать вывод: неполное квадратное уравнение вида ax2 = 0 равносильно уравнению x2 = 0, поэтому имеет единственный корень: x = 0. 4. Обобщение решений неполных квадратных уравнений различных видов. Можно предложить учащимся составить таблицу, из которой четко будет видно, как решаются неполные квадратные уравнения различных видов. | Коэффициент, равный нулю | b = 0 | c = 0 | b = 0 и c = 0 | | Вид | ax2 + c = 0 | ax2 + bx = 0 | ax2 = 0 | | Решение | ax2 = –c 
| x(ax + b) = 0 х = 0 или
ax + b = 0 | x2 = 0 | | Корни | Если  0, то корней нет. 0, то корней нет. Если  | х = 0; х =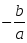 | х = 0 |
| 






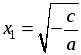 и
и 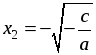 . Эти корни – противоположные числа.
. Эти корни – противоположные числа.









