Ученическая работа по теме "Движения"

МБОУ «Видновская СОШ №5 с УИОП»

ДВИЖЕНИЯ

Работа по геометрии Лосевой Татьяны

Движение

- преобразование плоскости или пространства, не изменяющее расстояния между точками;

- такое отображение фигуры, при котором каждым двум ее точкам A и B соответствуют такие точки A' и B', что |A'B'| = |AB|.

Общие свойства движения

1) Сохранение прямолинейности

2) Образом отрезка при движении является отрезок

3)Образом прямой при движении является прямая, а образом луча – луч

4) При движении образом треугольника является равный ему треугольник, образом плоскости - плоскость, причем параллельные плоскости отображаются на параллельные плоскости, образом полуплоскости – полуплоскость

5)При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины. Аналогичное верно и для двугранных углов.

Виды движений на плоскости

• Симметрия: -осевая, -центральная, -скользящая, -зеркальная.
• Параллельный перенос.
• Поворот.
• Инверсия.

ИНВЕРСИЯ

• (от лат. inversio — обращение) особый вид отображения плоскости или пространства посредством обратных радиусов, при котором окружности и сферы переходят в окружности и сферы.
• Инверсия превращает внутреннюю область окружности во внешнюю, и обратно.

Инверсия в графиках функций

Построение инверсии

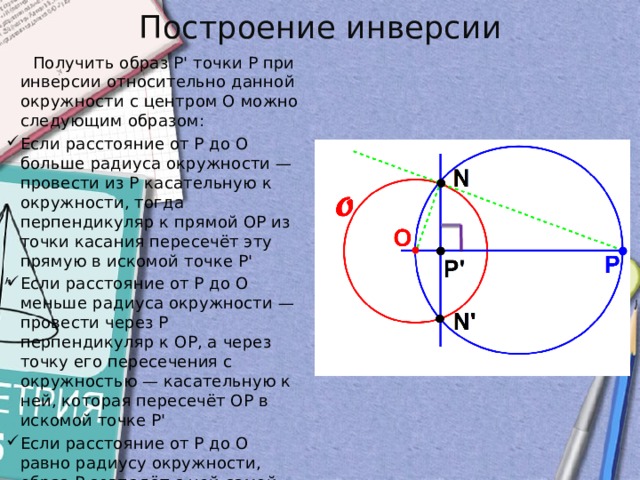
Получить образ P' точки P при инверсии относительно данной окружности с центром O можно следующим образом:

• Если расстояние от P до O больше радиуса окружности — провести из P касательную к окружности, тогда перпендикуляр к прямой OP из точки касания пересечёт эту прямую в искомой точке P'
• Если расстояние от P до O меньше радиуса окружности — провести через P перпендикуляр к OP, а через точку его пересечения с окружностью — касательную к ней, которая пересечёт OP в искомой точке P'
• Если расстояние от P до O равно радиусу окружности, образ P совпадёт с ней самой

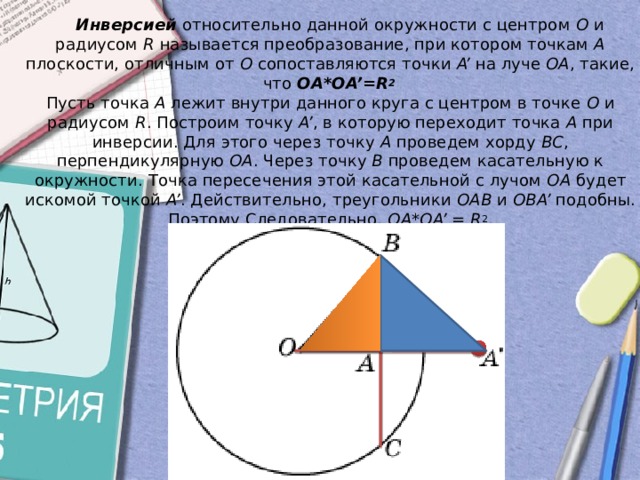
Инверсией относительно данной окружности с центром O и радиусом R называется преобразование, при котором точкам A плоскости, отличным от O сопоставляются точки A’ на луче OA , такие, что OA*OA’=R 2 Пусть точка A лежит внутри данного круга с центром в точке O и радиусом R . Построим точку A’ , в которую переходит точка A при инверсии. Для этого через точку A проведем хорду BC , перпендикулярную OA . Через точку B проведем касательную к окружности. Точка пересечения этой касательной с лучом OA будет искомой точкой A’ . Действительно, треугольники OAB и OBA’ подобны. Поэтому Следовательно, OA*OA’ = R 2 .

Свойства инверсии

1) При инверсии относительно окружности с центром в точке O точки A , B переходят в точки A’ , B’ такие, что треугольники OAB и OB’A’ подобны.

Действительно, в этом случае OА*OA’ = R 2 = OB* OB’. Значит, треугольники OAB и OB’A’ подобны.

Свойства инверсии

2) При инверсии относительно окружности с центром в точке O окружности, проходящие через точку O (без самой точки O ), переходят в прямые, не проходящие через точку O .

Действительно, пусть OA – диаметр окружности, проходящей через точку O , B – точка, принадлежащая этой окружности . Тогда угол OBA равен 90 и равен углу OA’B’ . Следовательно, точка B’ принадлежит прямой, проходящей через точку A’ и перпендикулярной OA .

Свойства инверсии

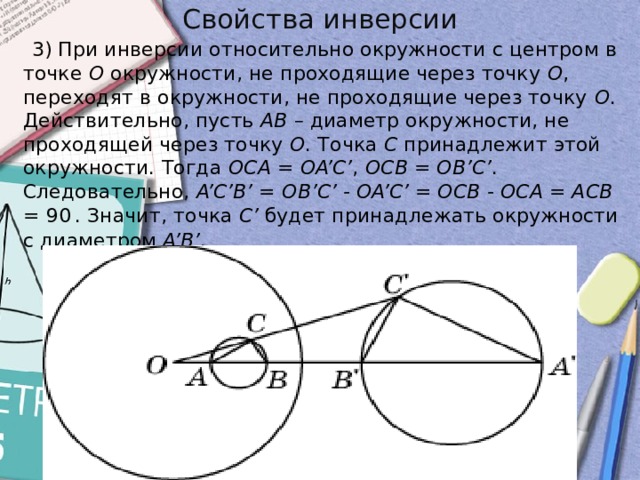
3) При инверсии относительно окружности с центром в точке O окружности, не проходящие через точку O , переходят в окружности, не проходящие через точку O . Действительно, пусть AB – диаметр окружности, не проходящей через точку O . Точка C принадлежит этой окружности. Тогда OCA = OA’C’ , OCB = OB’C’ . Следовательно, A’C’B’ = OB’C’ - OA’C’ = OCB - OCA = ACB = 90 . Значит, точка C’ будет принадлежать окружности с диаметром A’B’ .

Свойства инверсии

4)Заметим, что две окружности с центрами O , P и радиусами R , r перпендикулярны, если углы OAP и OBP – прямые. Значит, расстояние OP между центрами перпендикулярных окружностей равно .

Понятие инверсии встречается не только в геометрии, но еще и в литературе, русском языке, генетике, химии, биологии, спорте, медицине, географии и др. А общим в определении инверсии является «взаимодействие противоположностей» и «конструкция с обратным порядком» .

Инверсия в архитектуре

Сооружение из досок под названием «Инверсия» представлено в виде единой горизонтальной воронки, которая заканчивается в маленькую дыру, которая проходит через два бунгало

50 лет назад в Америке был разработан новый способ кровли плоской крыши – инверсионная кровля. При обычной кровле кладут 3 основных слоя: пароизоляционный, теплоизоляционный, гидроизоляционный. Инверсионная кровля предусматривает укладку этих слоев в обратном порядке. При этом могут добавляться дополнительные слои. Такая конструкция предусматривает долгую службу и повторное применение материала, надежную теплоизоляцию и защиту от механических воздействий.

Инверсия в литературе

Инверсия: Белеет парус одинокий В тумане моря голубом

Обычное строение предложения: В тумане голубого моря белеет одинокий парус

Инверсия в биологии

Инверсия  —  хромосомная   перестройка, при которой происходит поворот участка  хромосомы  на 180°

400 лет до н.э.

Гиппократ, прародитель медицины, использовал инверсию таким образом, что поднимал пациентов на лестницу с помощью комбинации ремней и блоков, используя силу гравитации для растягивания тела и излечения болезни.

Спектр применения инверсионного оборудования широк: его используют тысячи людей по всему миру, клиники и санатории, спортсмены и олимпийские сборные, также инверсию применяют и в армии США. После многих лет борьбы за восстановление репутации инверсионной терапии мы становимся свидетелями небывалого роста популярности  инверсионных тренажеров в начале 21 века, устраняющих боли в спине.

Используемые ресурсы и литература

• http://geometry2006.narod.ru/Problems/parkety.htm
• http://xreferat.ru/54/983-1-preobrazovaniya-ploskosti-dvizheni
• http://ru.wikipedia.org/wiki/%C8%ED%E2%E5%F0%F1%E8%FF_(%E3%E5%EE%EC%E5%F2%F0%E8%FF)
• http://www.aari.nw.ru/resources/m0001/Meteorology/HTML/PRIMER/GLOSSARY/TERMS/inversion.htm