Тема урока: Урок одной задачи
Учитель: Турова Оксана Владимировна
Класс: 9 класс
Предмет: геометрия
Актуальность:
Урок одной задачи – это поиск разных способов решения одной задачи. Ученик имеет возможность найти тот способ решения, который ему понятен. Учет подструктур математического мышления побуждает учащихся к поиску различных приемов решения. Психологи установили, что решение одной задачи разными способами приносит больше пользы, чем решение подряд нескольких однотипных задач.
Цели урока:
Решить задачу несколькими способами, учитывая структуры математического мышления. Показать многообразие и красоту математических решений. Создать ситуацию успеха и радости.
Задачи урока:
Образовательные: обобщить изученный по теме материал, формировать умение применять знания к решению задач;
Развивающие: развивать познавательную активность, творческие способности и интерес к предмету. Индивидуальные способности и критическое мышление;
Воспитательные: учить прислушиваться к мнению товарищей, развивать умение работать в группах, воспитывать у учащихся гибкость мышления.
План урока.
Организационный момент (2 мин);
Решение задач в группах (15 мин);
Представление решения членами группы (20 мин);
Заключительное слово учителя (5 мин);
Рефлексия, домашнее задание (3 мин).
Ход урока.
Организационный момент
Учитель объясняет учащимся, что сегодня предстоит необычный урок. Решая задачу по группам и защищая свое решение, они смогут увидеть большие возможности геометрии, когда одну и ту же задачу можно решить разными способами.
Затем учащимся предлагается сесть по группам, выбрать капитана, который будет представлять решение задачи на доске.
Перед уроком класс разбивается на 5 групп (на основе диагностики) по доминантным подструктурам математического мышления: на «топологов», «метристов», «порядковцев» и «алгебраистов».
Решение задач и в группах
Учитель предлагаем приступить к решению задачи.
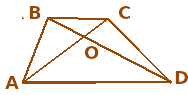 Задача:
Задача:
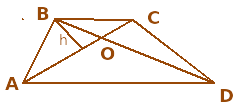
Трапеция разбита диагоналями на четыре треугольника. Докажите, что треугольники, прилежащие к боковым сторонам, равновелики.
В процессе урока учитель подходит к отдельным группам и наблюдает за работой учеников. Роль учителя заключается в том, чтобы в зависимости от доминантного кластера математического мышления детей той или иной группы, найти те подсказки, которые окажут реальную помощь школьникам.
Для группы с доминантной топологической подструктурой естественной подсказкой может быть акцент на использование принадлежности одних треугольников другим, а именно:
- Не видите ли вы треугольник, в который включаются треугольники АОВ и СОD?
- Площади каких фигур включает в себя S△ABD ? (S△AСD ?)
-Что является пересечением △АВD и △АСD?
Обычно топологи, опираясь на подсказки, выстраивают следующее доказательство:
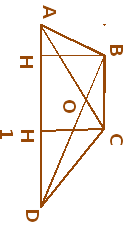
Доказательство:
Рассмотрим △АВD и △ACD.
У них общее основание АD и равны высоты ВН=СН1, тогда
S△ABD =S△ACD
S△ABO = S△ABD - S△AOD = S△ACD - S△AOD = S△CDO
S△ABO = S△CDO
Алгебраическая подструктура позволяет осуществлять не только прямые, но и обратные операции, заменить несколько операций одной, вычислить части и собрать их в единое целое. Для них удобны следующие подсказки:
- Используйте метод от противного;
-Проведите через точку О отрезок MN ││ BC и докажите, что OM=ON
Группой алгебраистов были представлены следующие решения:
I способ:
 Пусть S△ABO ≠ S△CDO, тогда S△ABD ≠ S△ACD и ВС ││ АD.
Пусть S△ABO ≠ S△CDO, тогда S△ABD ≠ S△ACD и ВС ││ АD.
Получили противоречие с тем, что АВСД трапеция. Значит, S△ABO = S△CDO
II способ:
Проведем MN ││ BC, О MN, OM=ON
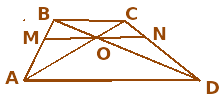 Треугольники АВО и СВО состоят из двух треугольников, площади которых равны.
Треугольники АВО и СВО состоят из двух треугольников, площади которых равны.
S△AМO = S△NDO, S△ВМO = S△CNO
Тогда ,S△ABO = S△CDO
Метрическая подструктура акцентирует внимание человека на количественных преобразованиях и позволяет пересчитывать, определять конкретные числовые значения.
Хорошей подсказкой является следующая:
-По формуле S△ =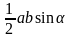 вычислите S△ABO и S△CDO, используя подобие △ВСО и △АДО
вычислите S△ABO и S△CDO, используя подобие △ВСО и △АДО
Решение «метристов»:
△ВСО ∽ △АДО, тогда
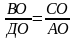 ,
,
АО·ВО =СО·ДО │·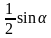
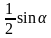 АО·ВО =
АО·ВО =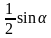 СО·ДО,
СО·ДО,
=∠АОВ = ∠СОД
S△ABO = S△CDO
Для проективистов очевидной и полезной будет подсказка:
- заменить («спроецировать») треугольники на одну из сторон каждого из них, то есть на отрезки диагоналей трапеции.
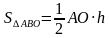
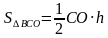
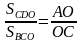
Аналогично, 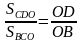
△ВСО ∽ △АДО, значит 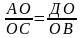 ,
,
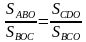
S△ABO = S△CDO
Для порядковцев важны такие отношения, как «больше-меньше», «равно». Они любят действовать последовательно, поэтому для них предлагаются подсказки:
- Установите последовательность величин площадей треугольников от большего к меньшему;
- Есть ли среди них треугольники с равными площадями?
- На каком основании вы можете заключить, что площадь каждого последующего треугольника меньше площади предыдущего?
- Попробуйте последовательно заменять площадь трапеции суммой площадей больших треугольников, а сумму последних – суммой площадей меньших треугольников;
Разные дети, после разного количества подсказок приходят к следующим решениям:
I способ:
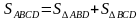
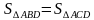
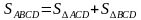
Тогда, 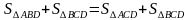
Заменяя площади больших треугольников площадями меньшими, получаем:
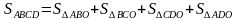 (1)
(1)
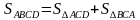
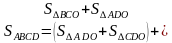 ) (2)
) (2)
Приравниваем правые части (1) и (2), приводим подобные слагаемые:
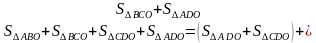 )
)
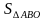 =
= 
II способ:
Используя формулу  , замечаем
, замечаем  =
= 
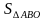 =
= 
Представление решения членами группы
Каждая группа выступает со своим доказательством.
Это очень важный этап урока, так как только после того как школьник усвоил решение адекватное своему кластеру, он способен осознанно и неформально овладеть другими способами решения.
Рефлексия. Домашнее задание.
Задача 2: Докажите, что медиана разбивает треугольник на шесть равновеликих треугольников.





 Задача:
Задача: 
 Пусть S△ABO ≠ S△CDO, тогда S△ABD ≠ S△ACD и ВС ││ АD.
Пусть S△ABO ≠ S△CDO, тогда S△ABD ≠ S△ACD и ВС ││ АD.  Треугольники АВО и СВО состоят из двух треугольников, площади которых равны.
Треугольники АВО и СВО состоят из двух треугольников, площади которых равны.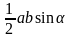 вычислите S△ABO и S△CDO, используя подобие △ВСО и △АДО
вычислите S△ABO и S△CDO, используя подобие △ВСО и △АДО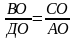 ,
,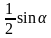

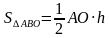
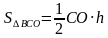
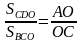
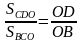
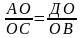 ,
,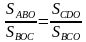
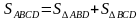
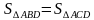
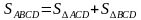
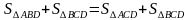
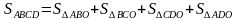 (1)
(1)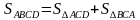
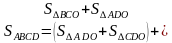 ) (2)
) (2)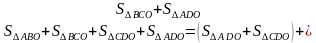 )
) 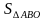 =
= 









