Билет №1
Верно ли высказывание:
а) Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему;
б) Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе;
в) Тангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.
г) Гипотенуза прямоугольного треугольника равна сумме катетов;
д) Гипотенуза – наибольшая сторона прямоугольного треугольника.
Докажите теорему:
Сформулируйте и докажите теорему о средней линии треугольника.
ОТВЕТ ПО РИСУНКУ: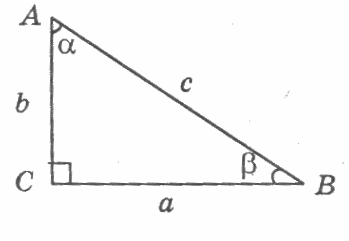
Используя рисунок, выбери правильный ответ
а) 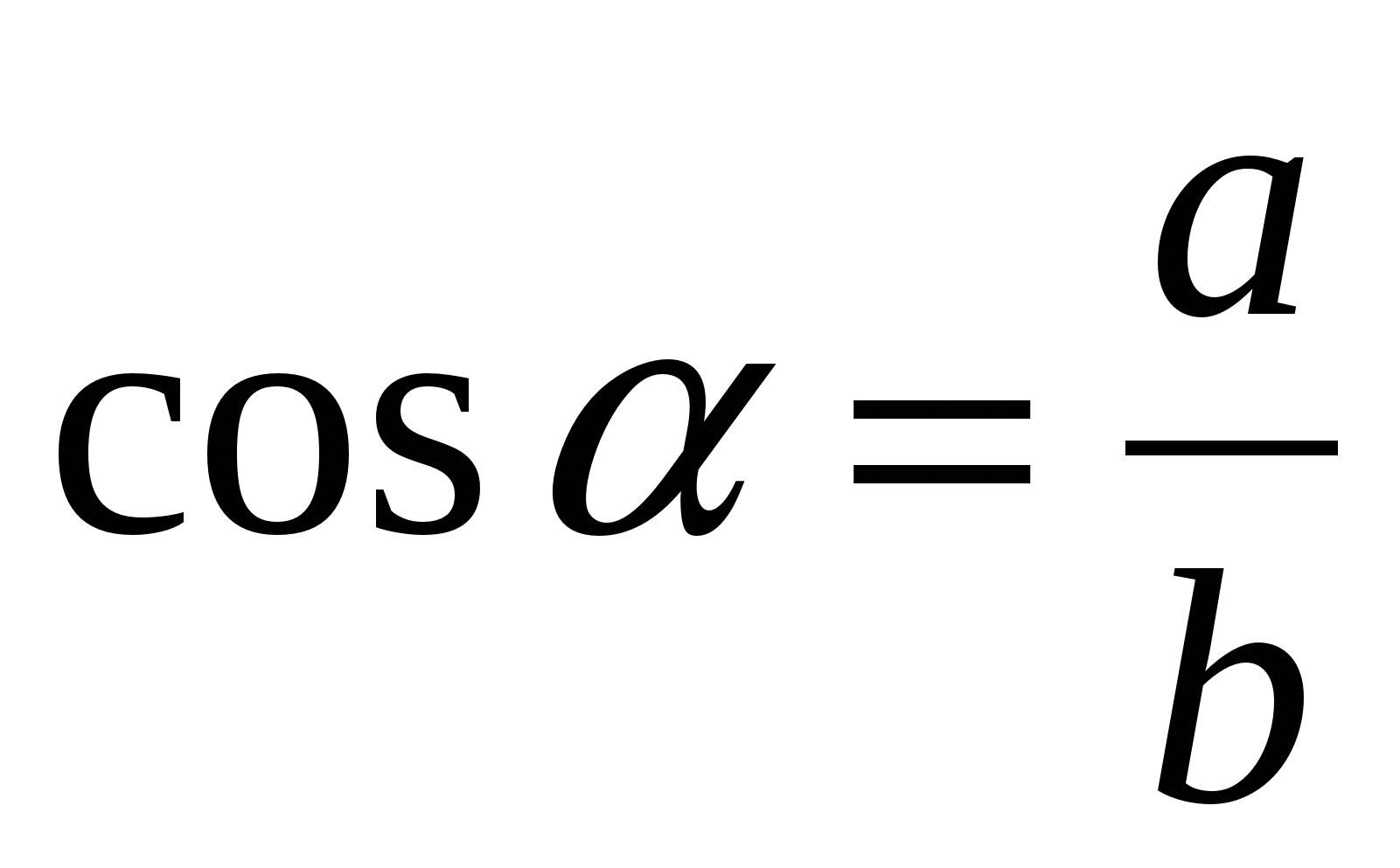 ; б)
; б) 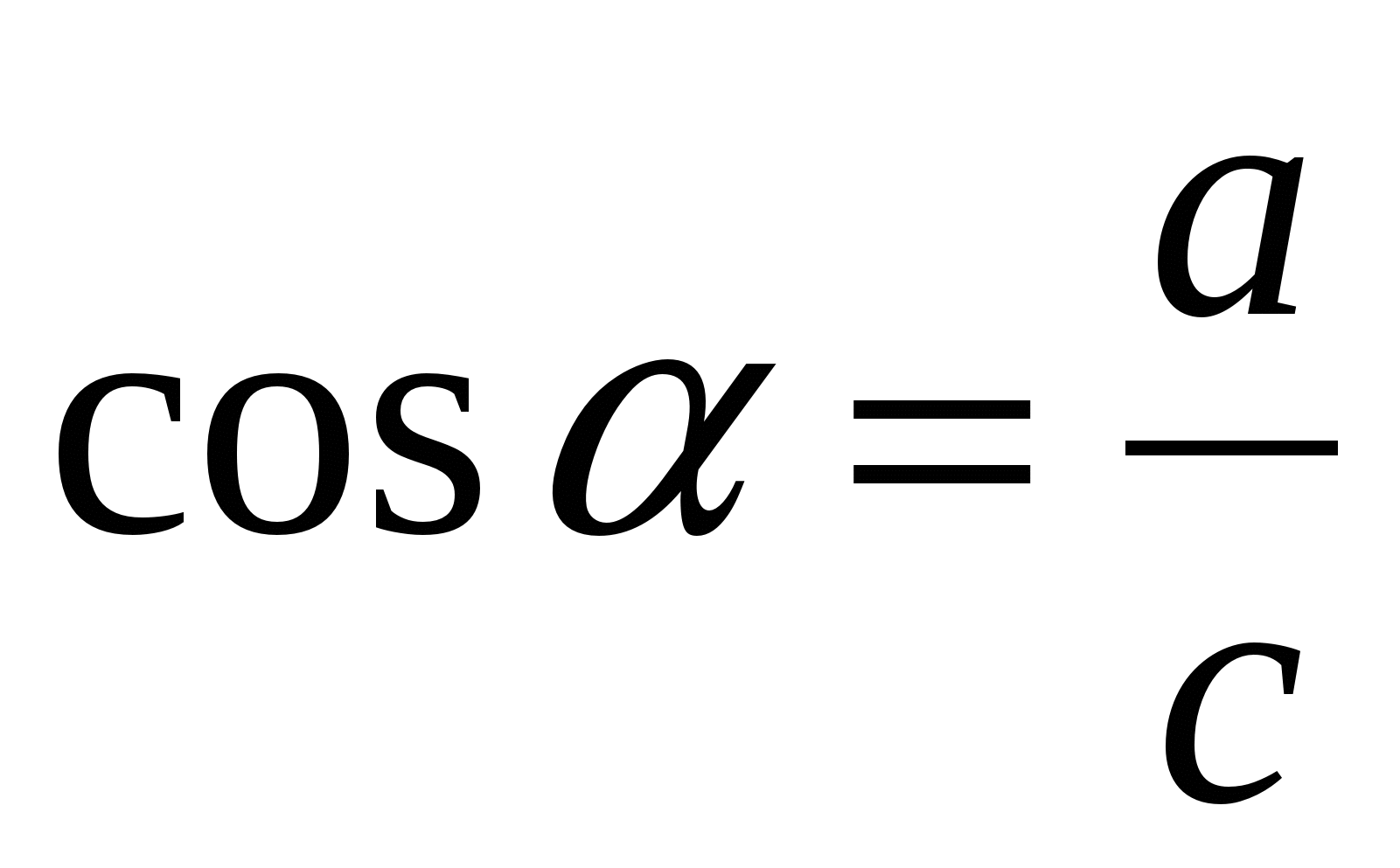 ; в)
; в) 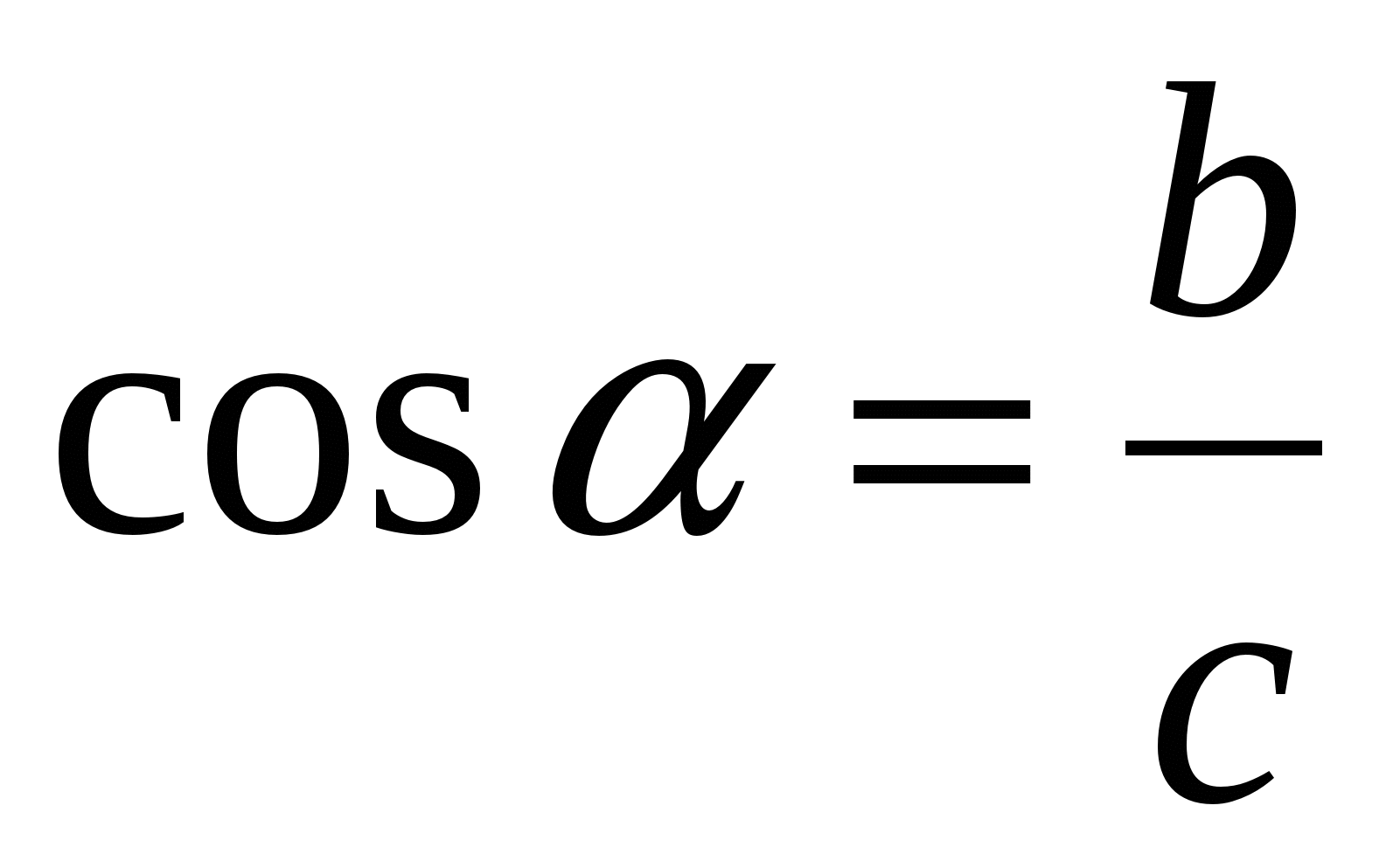 ; г)
; г) 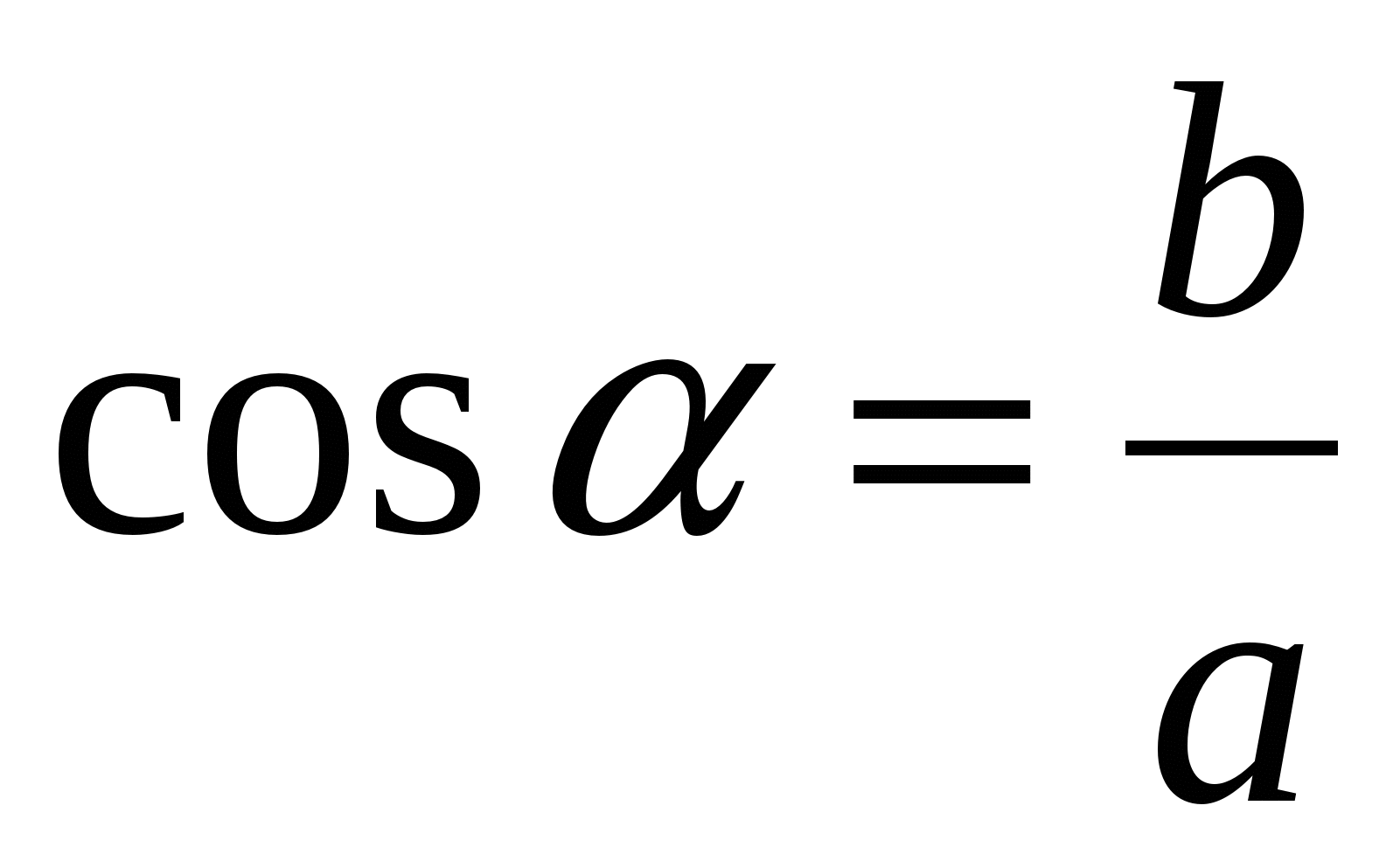 .
.
4) ЗАДАЧИ:
В треугольнике угол С=90, АВ=50, ВС=30. Найти cos А.
В равнобедренном треугольнике АВС с основанием АС проведена высота ВD. Найдите боковые стороны и высоту ВD, если угол А равен 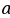 , AC=b.
, AC=b.
Билет №2
1) Верно ли высказывание:
а) Синусом острого угла прямоугольного треугольника называется отношение: прилежащего катета к противолежащему;
б) Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе;
в) Гипотенуза – наибольшая сторона прямоугольного треугольника;
г) Тангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему;
д) Гипотенуза прямоугольного треугольника равна сумме катетов.
2) Докажите теорему:
Сформулируйте и докажите утверждение о том, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на подобные треугольники.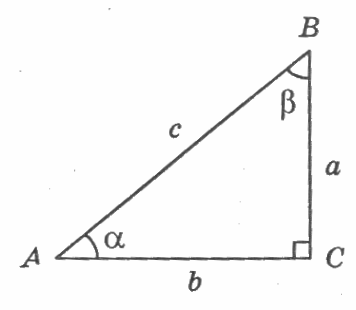
3) ОТВЕТ ПО РИСУНКУ:
Используя рисунок, выбери правильный ответ:
а) 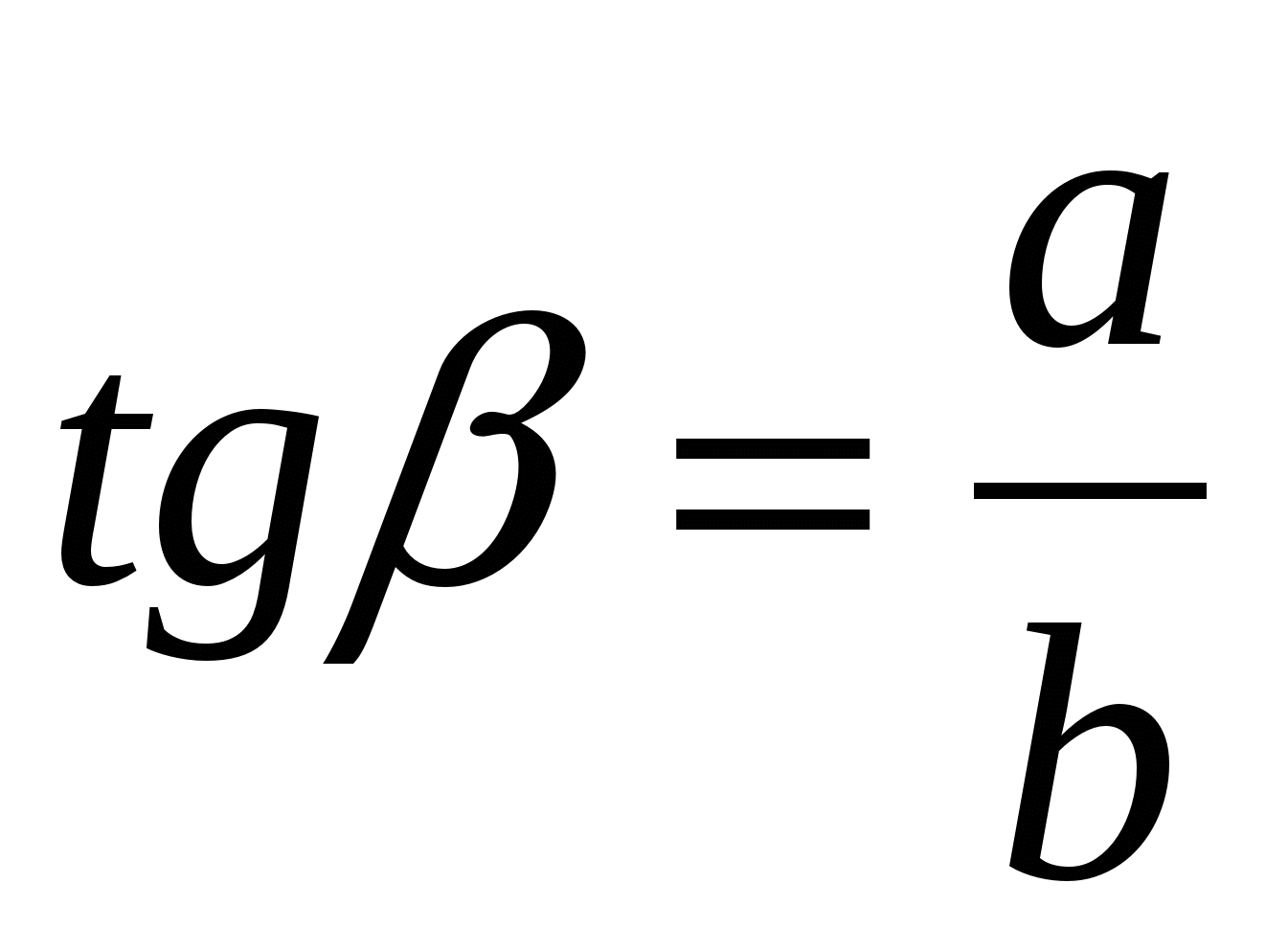 ; б)
; б) 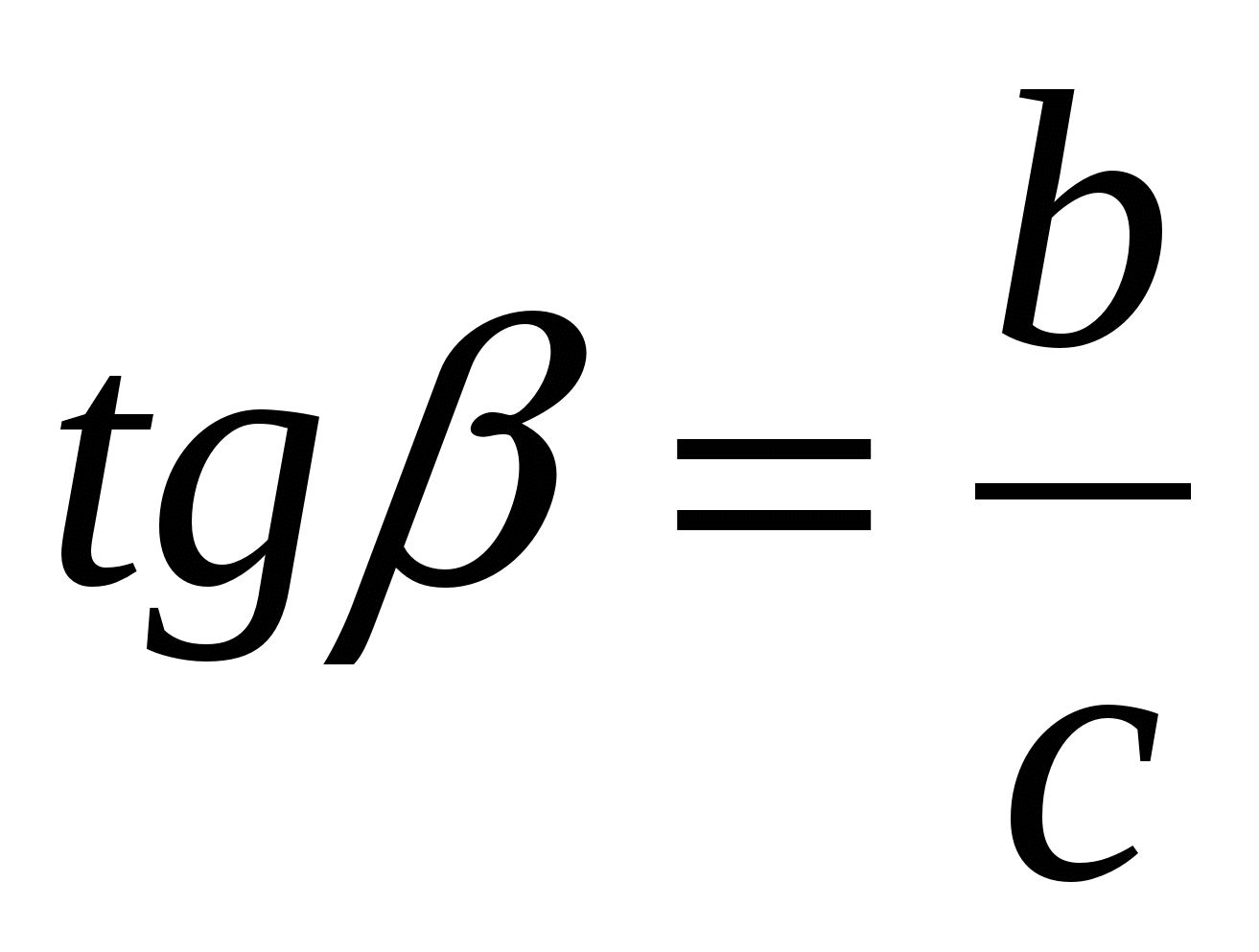 ; в)
; в) 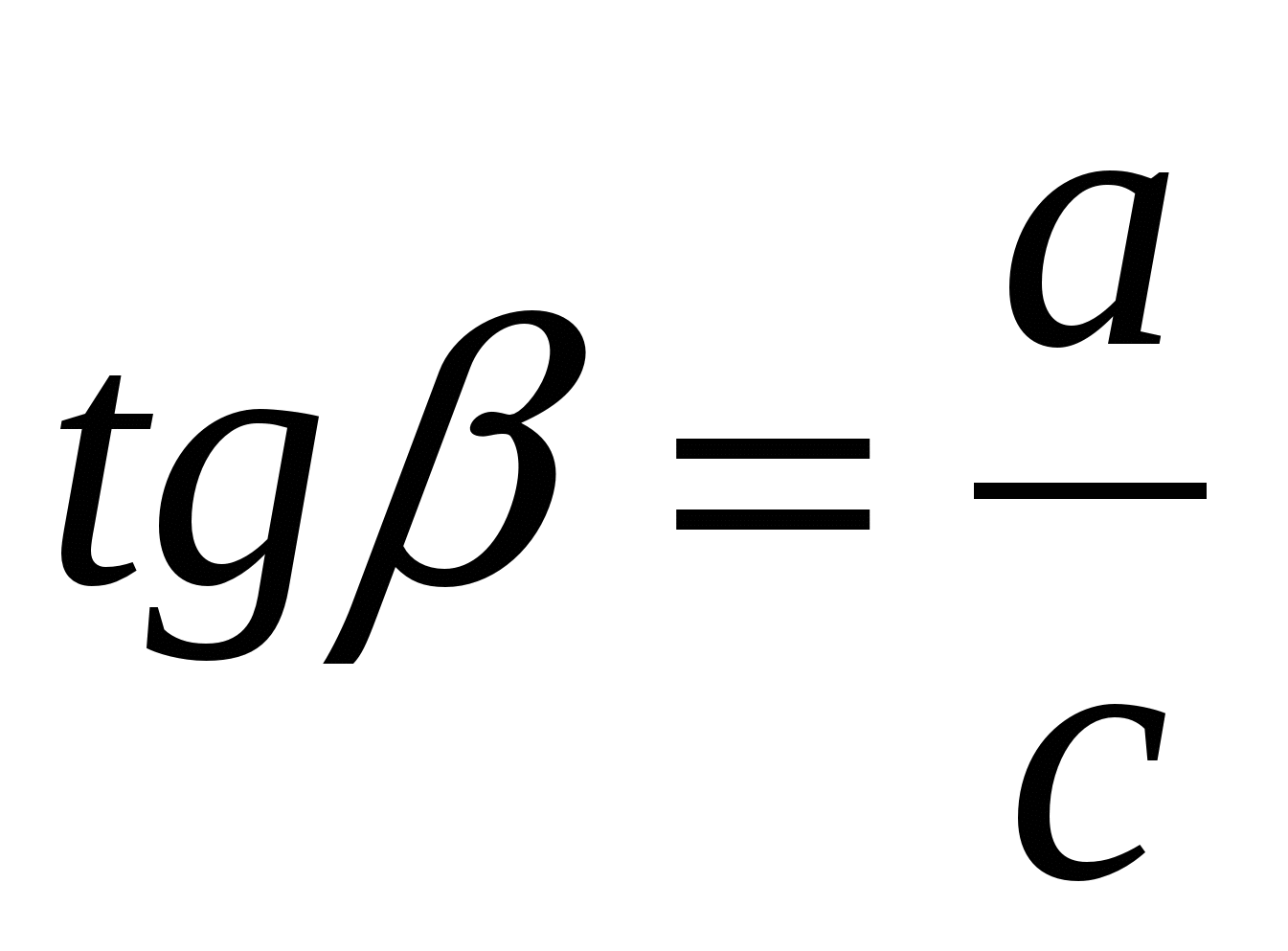 ; г)
; г) 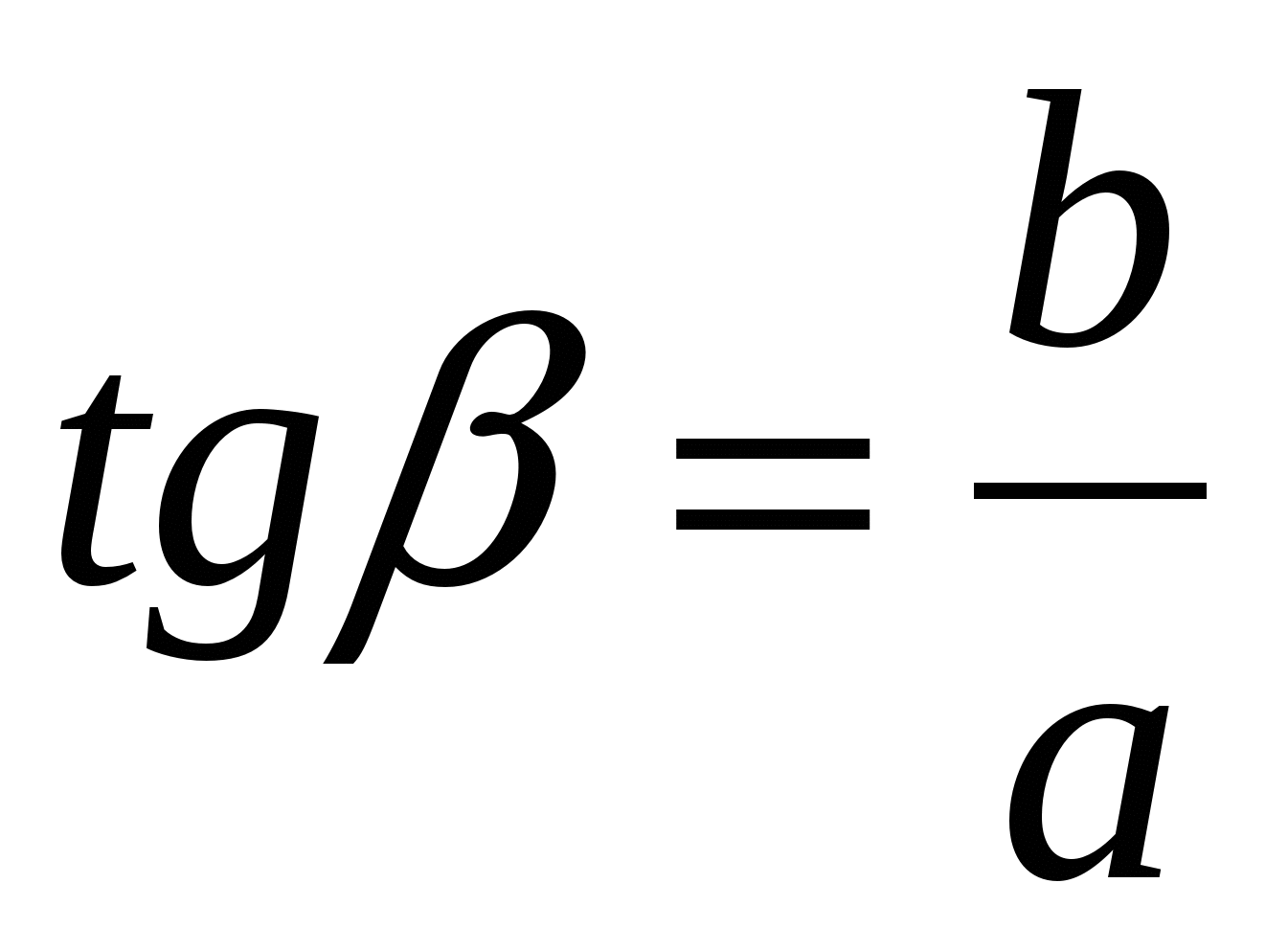
4) ЗАДАЧИ:
1) В треугольнике АВС, АС= ВС=10, АВ = 14. Найти cos А.
2) Один из углов ромба равен 600, а диагональ, исходящая из вершины этого угла, равна 10. Найдите вторую диагональ и сторону ромба.
Билет №3
1) Верно ли высказывание:
а) Синус острого угла прямоугольного треугольника равен косинусу другого острого угла данного треугольника;
б) Катет прямоугольного треугольника, лежащий против угла в 300 , равен половине гипотенузы;
в) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе;
г) Синусом острого угла прямоугольного треугольника называется отношение: прилежащего катета к гипотенузе;
д) Гипотенуза – наибольшая сторона прямоугольного треугольника.
2) Докажите теорему:
Сформулируйте и докажите утверждения о пропорциональных отрезках в прямоугольных треугольнике (одно на выбор).
3) ОТВЕТ ПО РИСУНКУ:
Используя рисунок, выбери правильный ответ:
а) 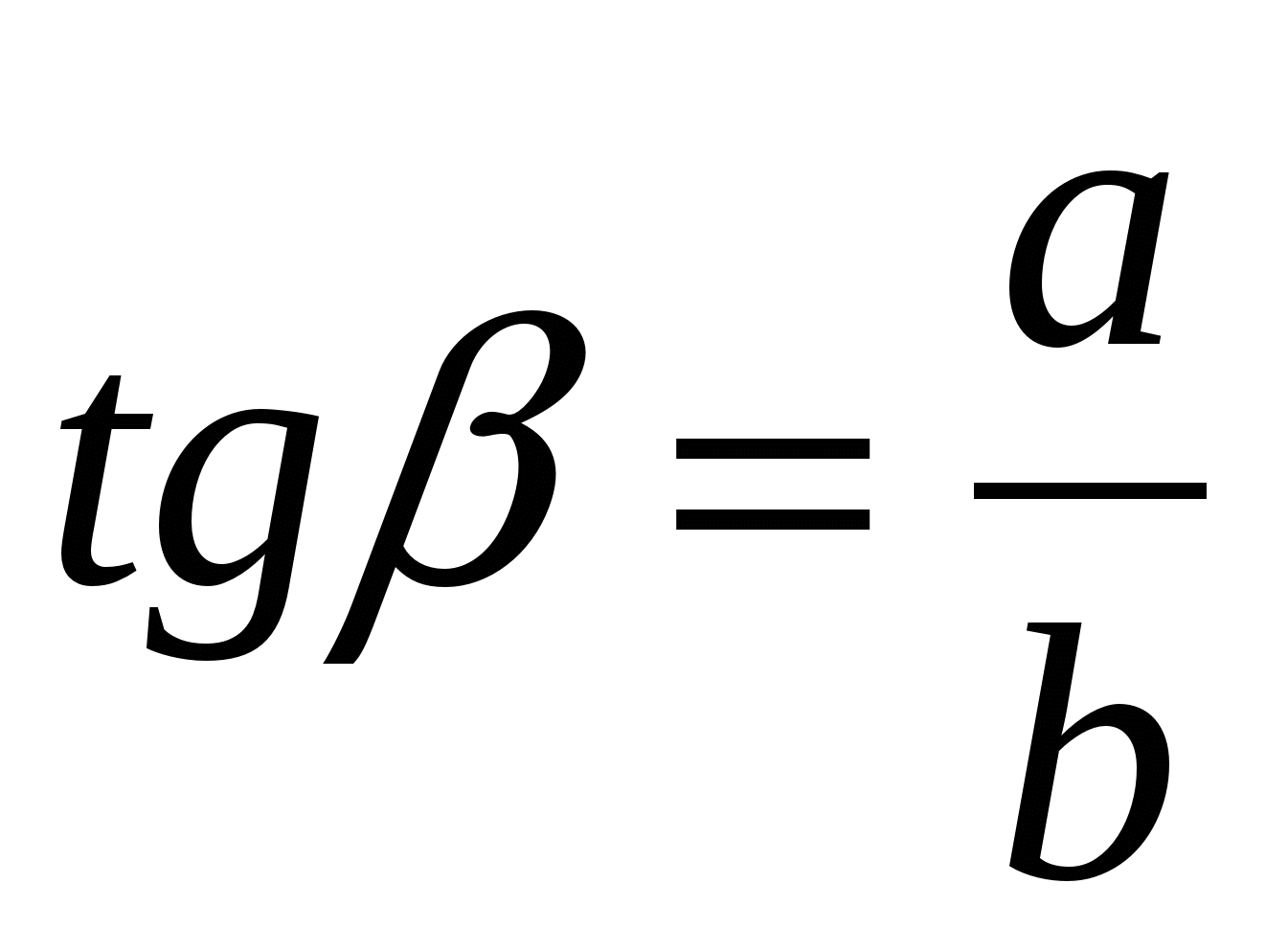 ; б)
; б) 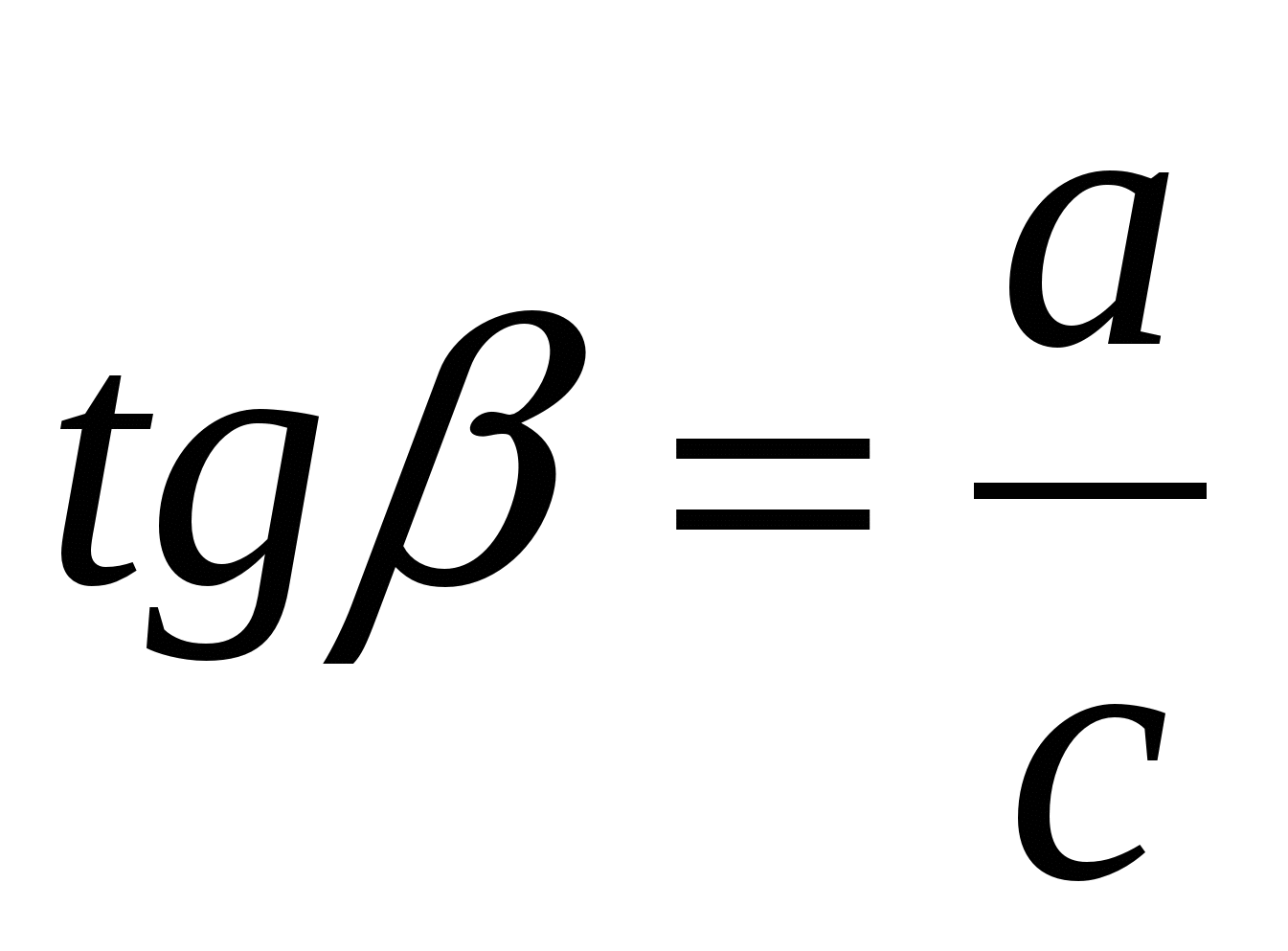 ; в)
; в) 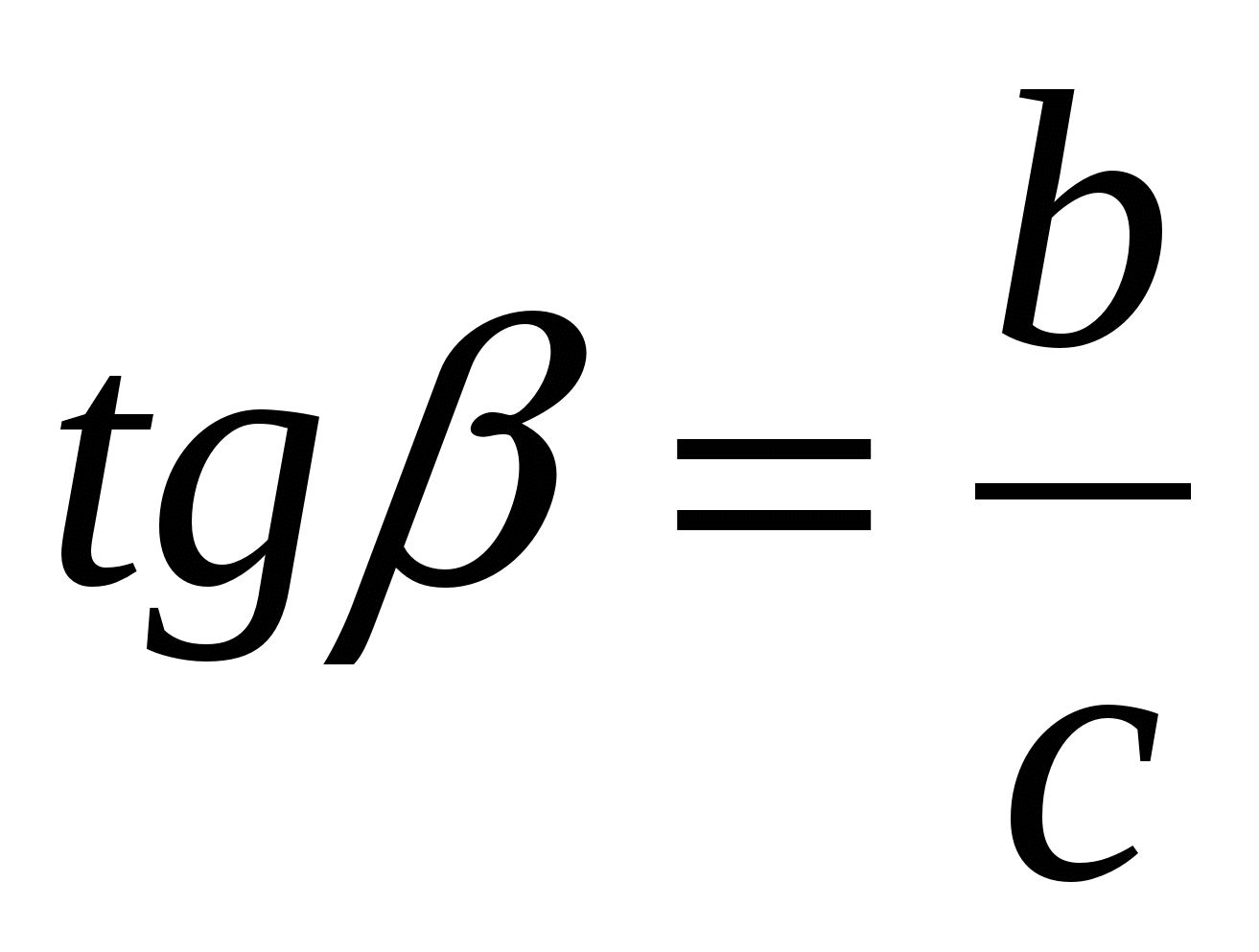 ; г)
; г) 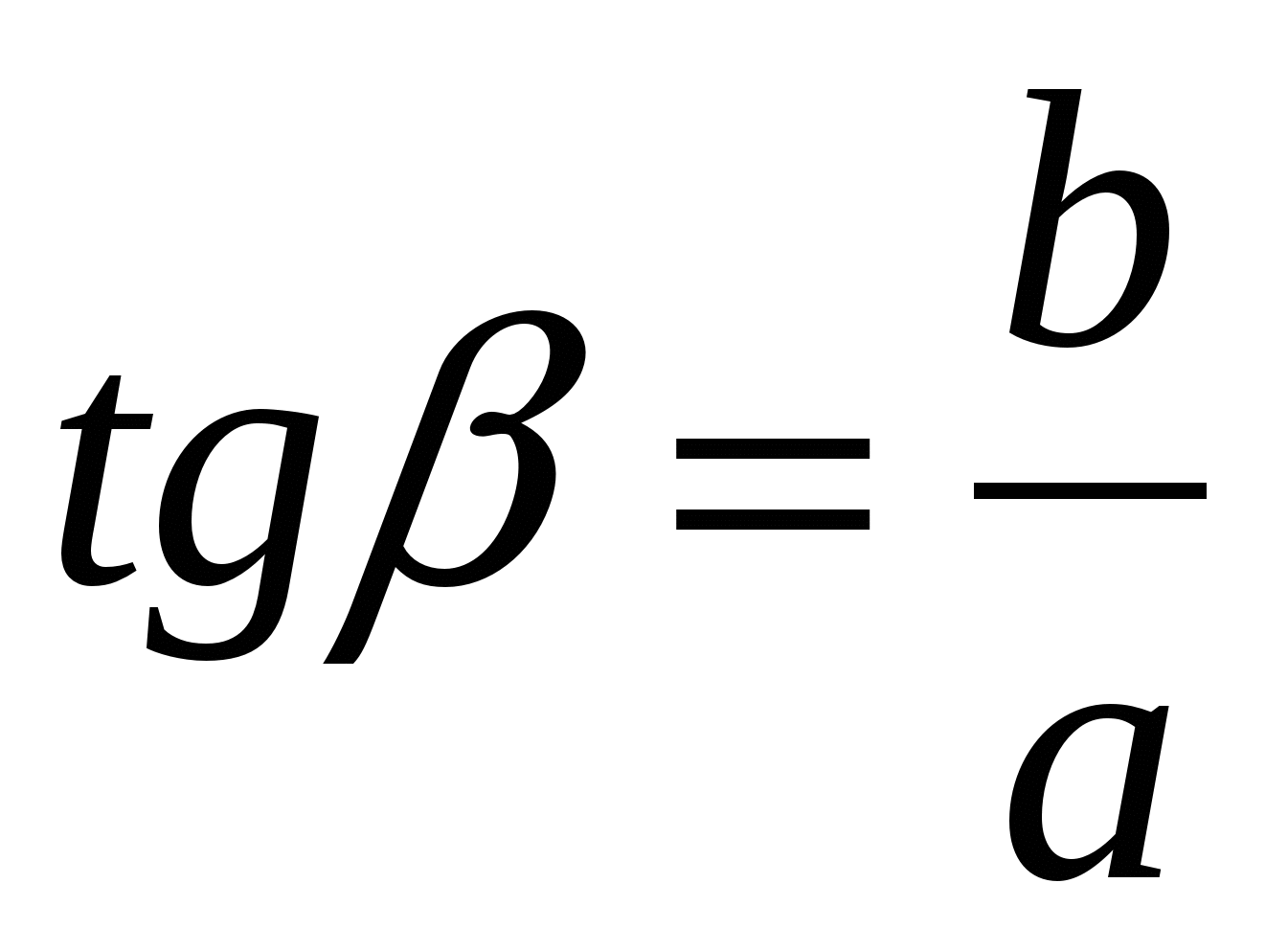 .
.
4) ЗАДАЧИ:
1) В треугольнике АВС угол С=90 АС=12 см, СВ=15. Найти tg A.
2) В равнобедренной трапеции MNKT большее основание MT=m, уголT равен 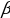 . Диагональ MK перпендикулярна стороне KT. Найти MN, NK, периметр и площадь трапеции.
. Диагональ MK перпендикулярна стороне KT. Найти MN, NK, периметр и площадь трапеции.
Билет №4
1) Верно ли высказывание:
а) Косинусом острого угла прямоугольного треугольника называется отношение катета к гипотенузе;
б) Синусом острого угла прямоугольного треугольника называется отношение: прилежащего катета к противолежащему;
в) Катет прямоугольного треугольника равен половине гипотенузы;
г) Гипотенуза прямоугольного треугольника равна сумме катетов;
д) Синус острого угла прямоугольного треугольника равен косинусу этого угла.
2) Докажите теорему:
Докажите, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
3) ОТВЕТ ПО РИСУНКУ:
Используя рисунок, выбери правильный ответ:
а) 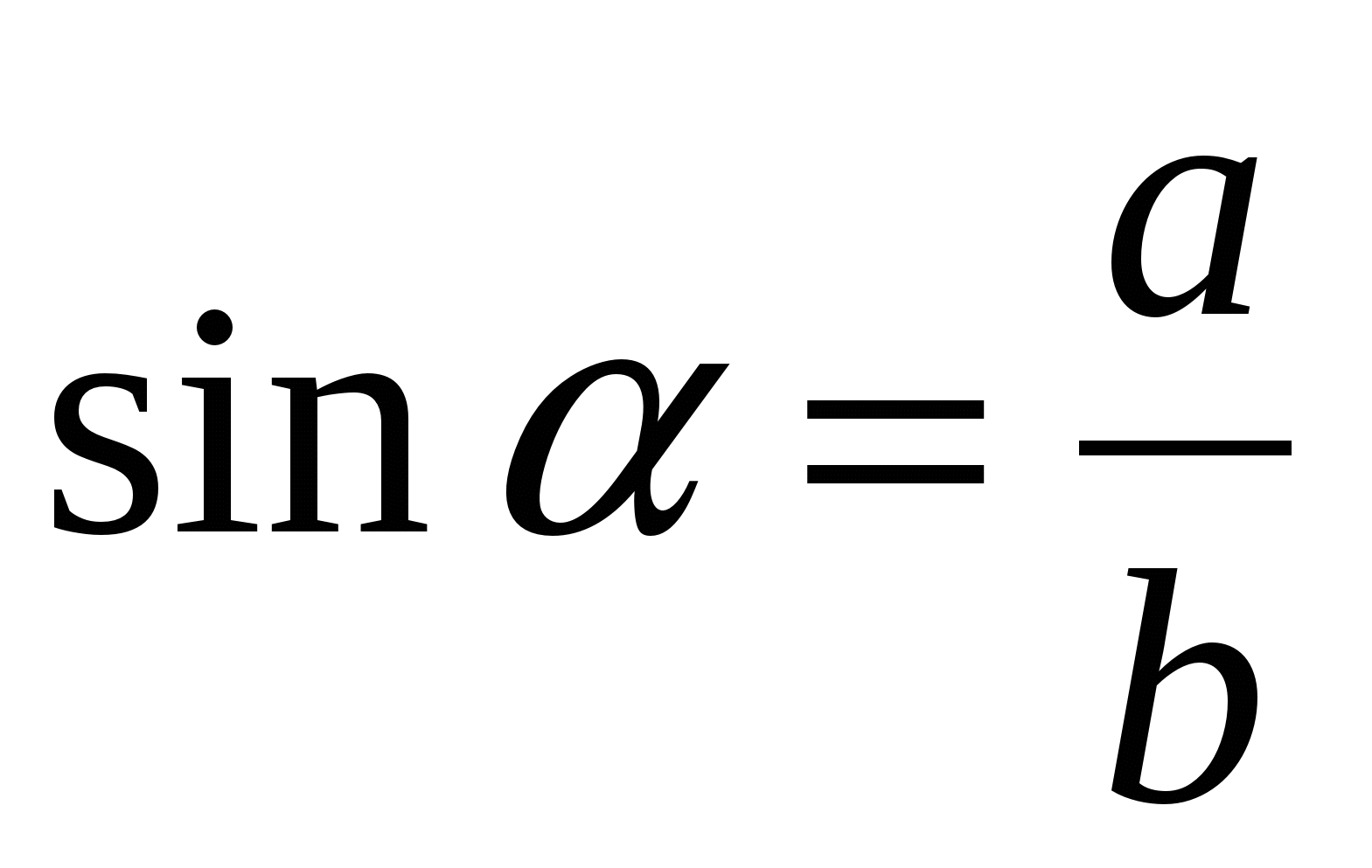 ; б)
; б) 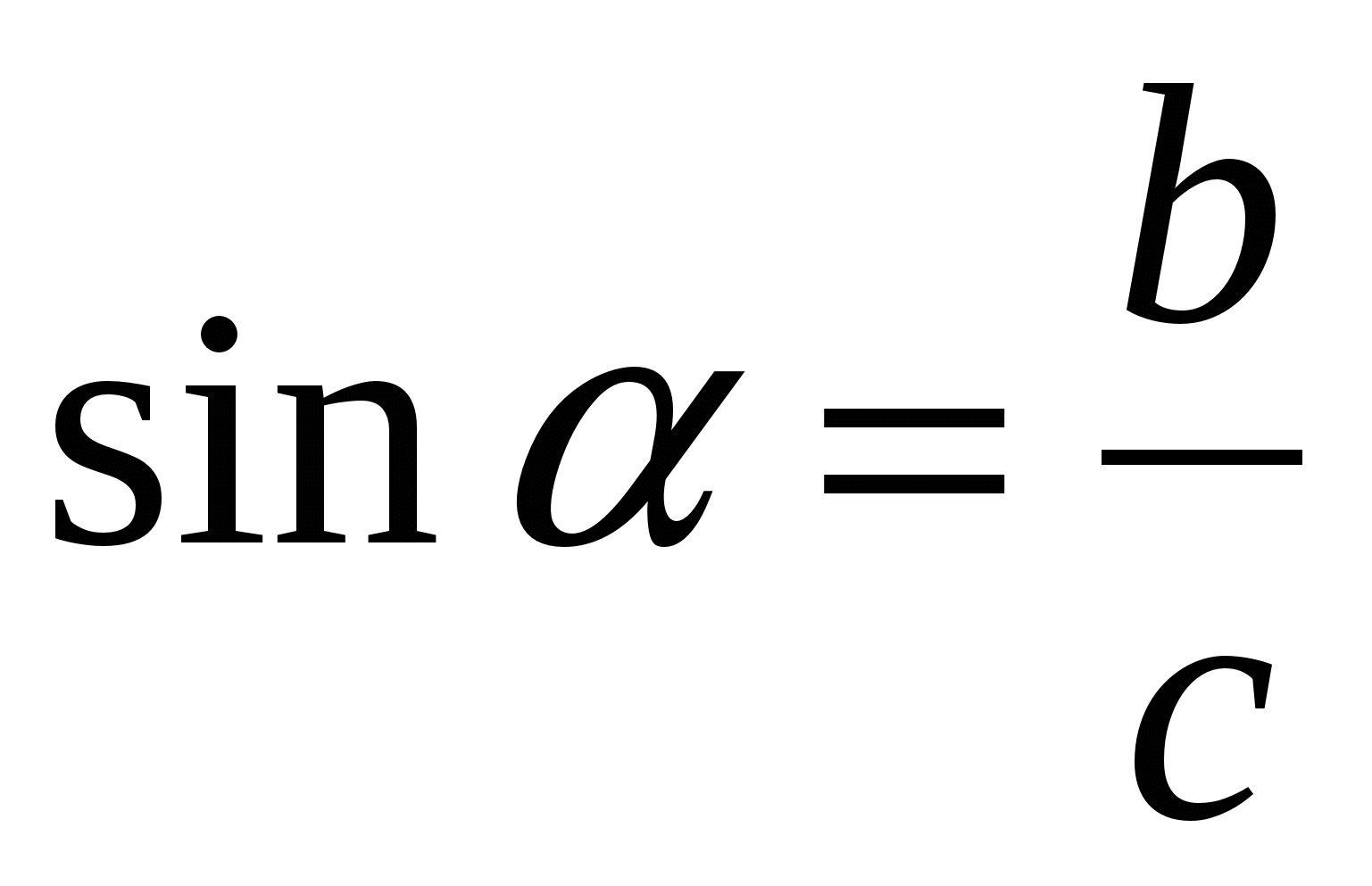 ; в)
; в) 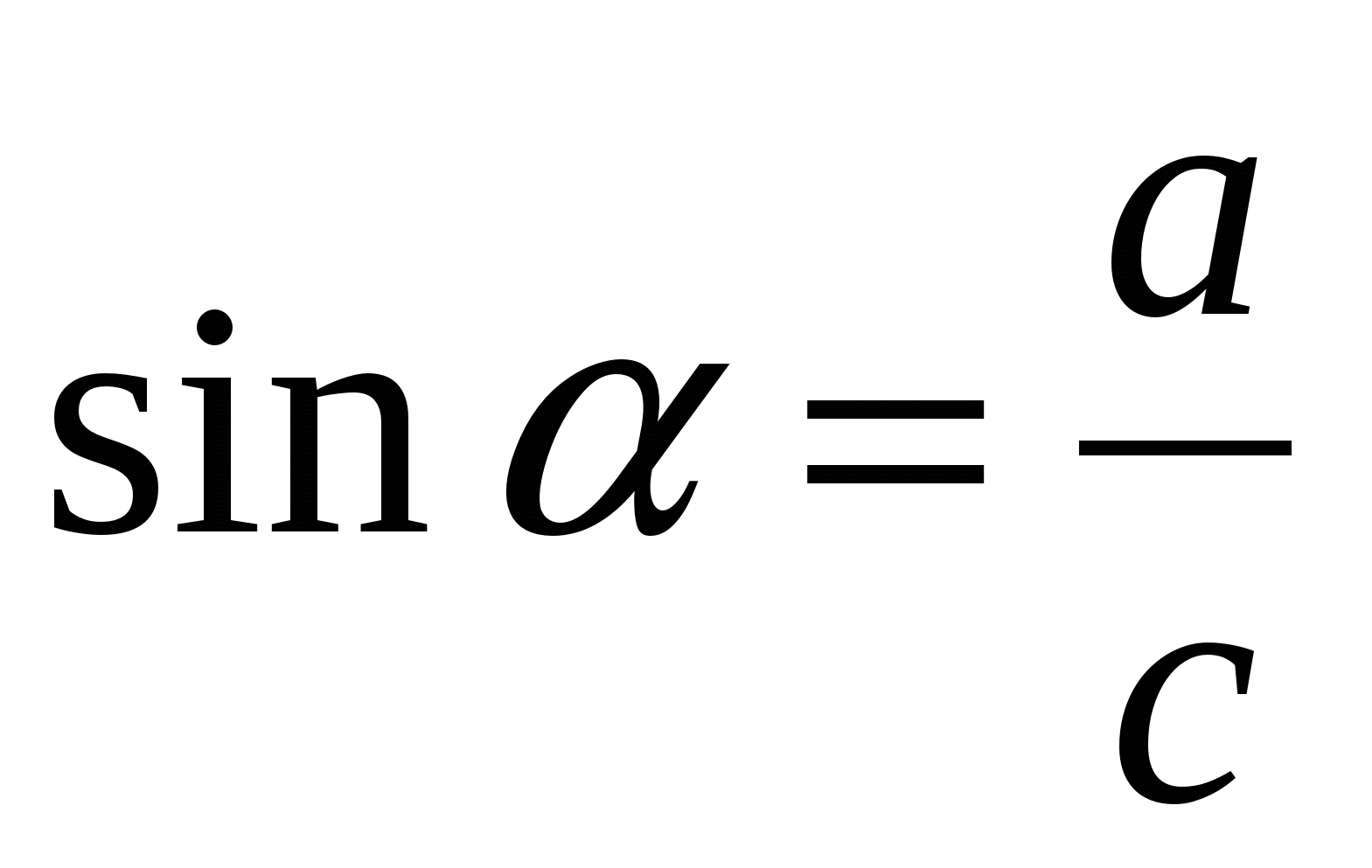 ; г)
; г) 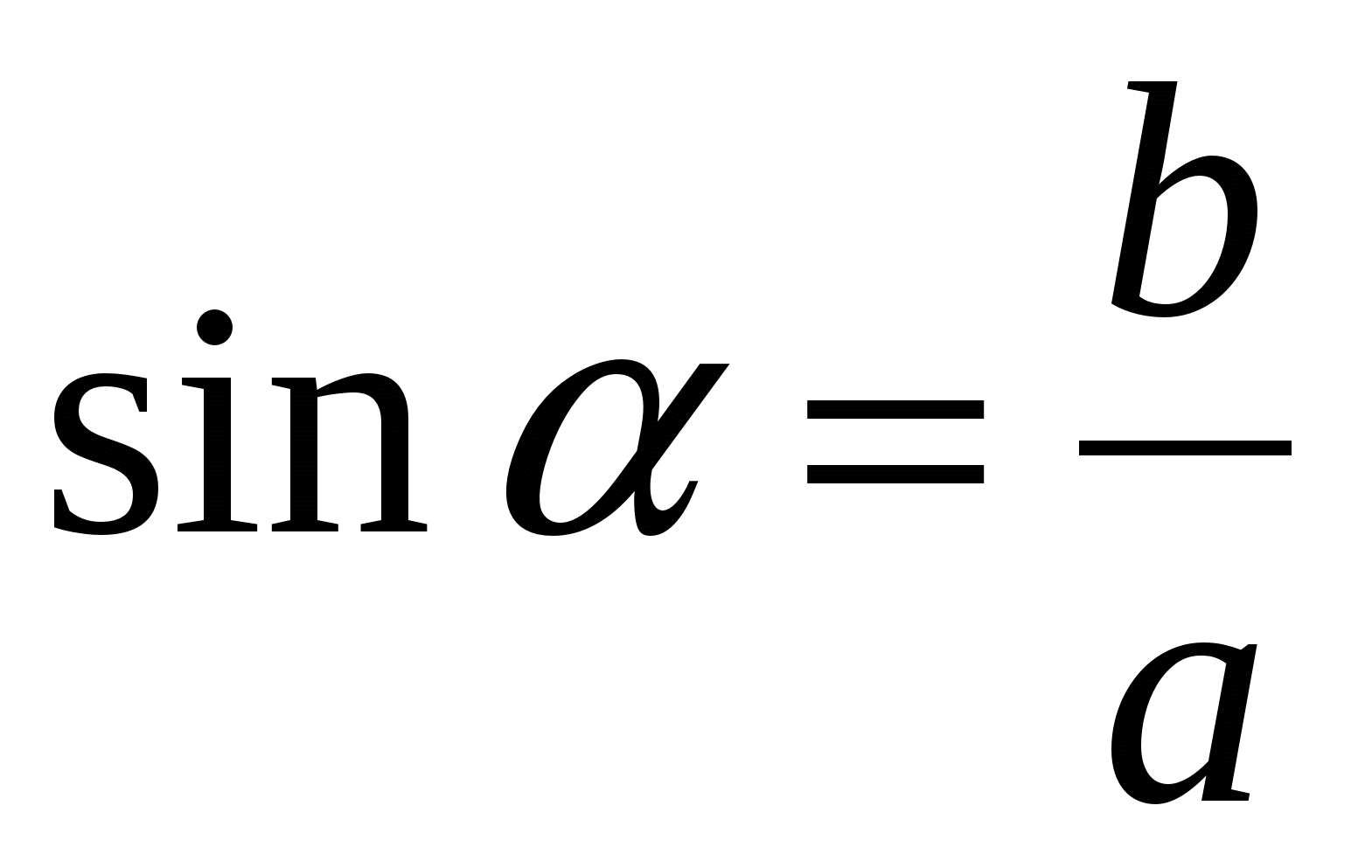 .
.
4) ЗАДАЧИ:
1) В треугольнике АВС, угол С=90 , АВ=20, ВС= 12. Найти cos А.
2) В равнобедренном треугольнике АВС с основанием АС проведена высота ВD. Найдите боковые стороны и основание, если 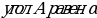 ВD=h.
ВD=h.
Билет №5
1) Верно ли высказывание:
а) Катет прямоугольного треугольника, лежащий против угла в 300 , равен половине гипотенузы;
б) Катет прямоугольного треугольника равен половине гипотенузы;
в) Синусом острого угла прямоугольного треугольника называется отношение: прилежащего катета к гипотенузе;
г) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе;
д) Гипотенуза – наибольшая сторона прямоугольного треугольника.
2) Докажите теорему:
Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
3) ОТВЕТ ПО РИСУНКУ:
Используя рисунок, выбери правильный ответ:
а) 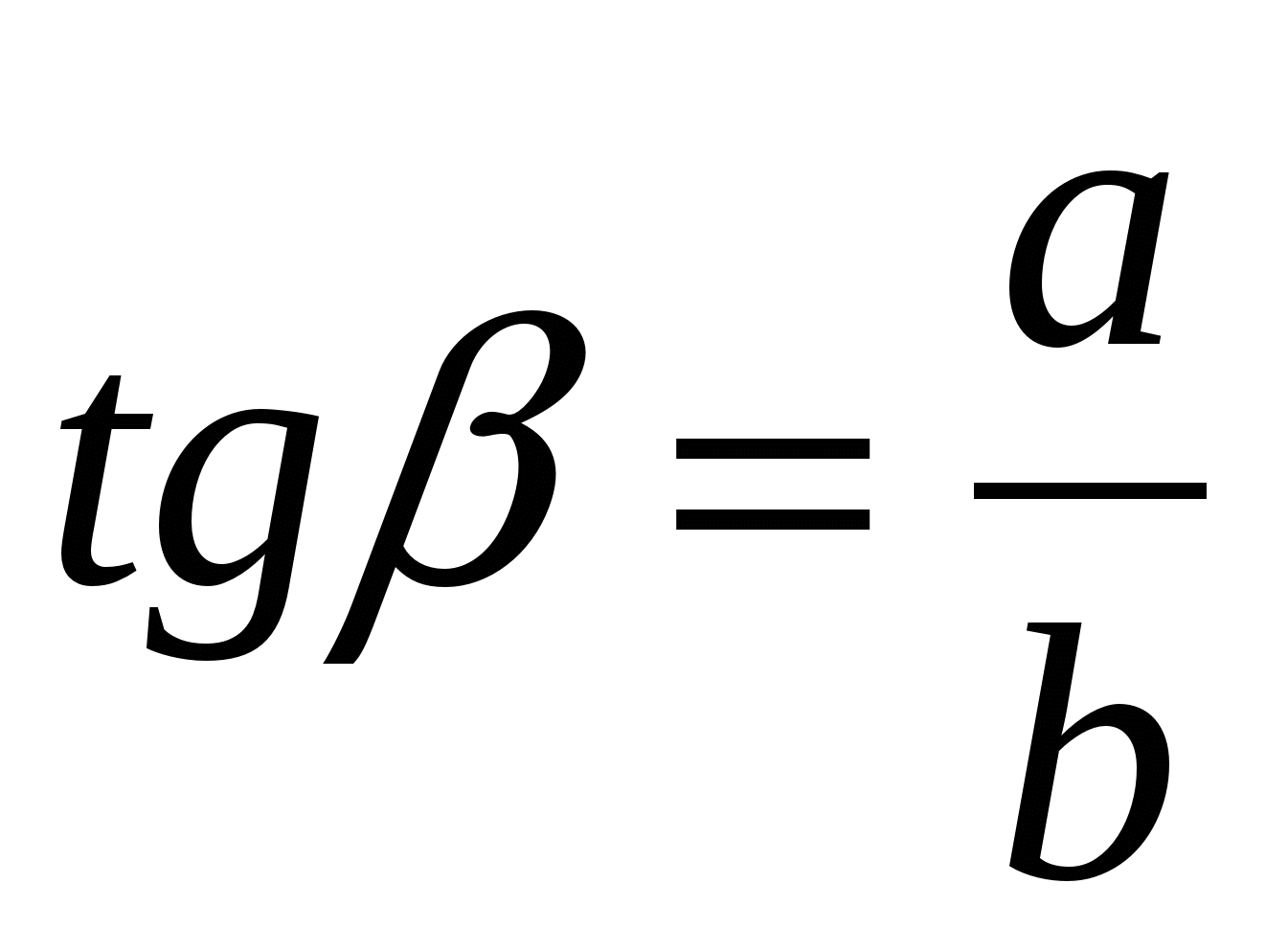 ; б)
; б) 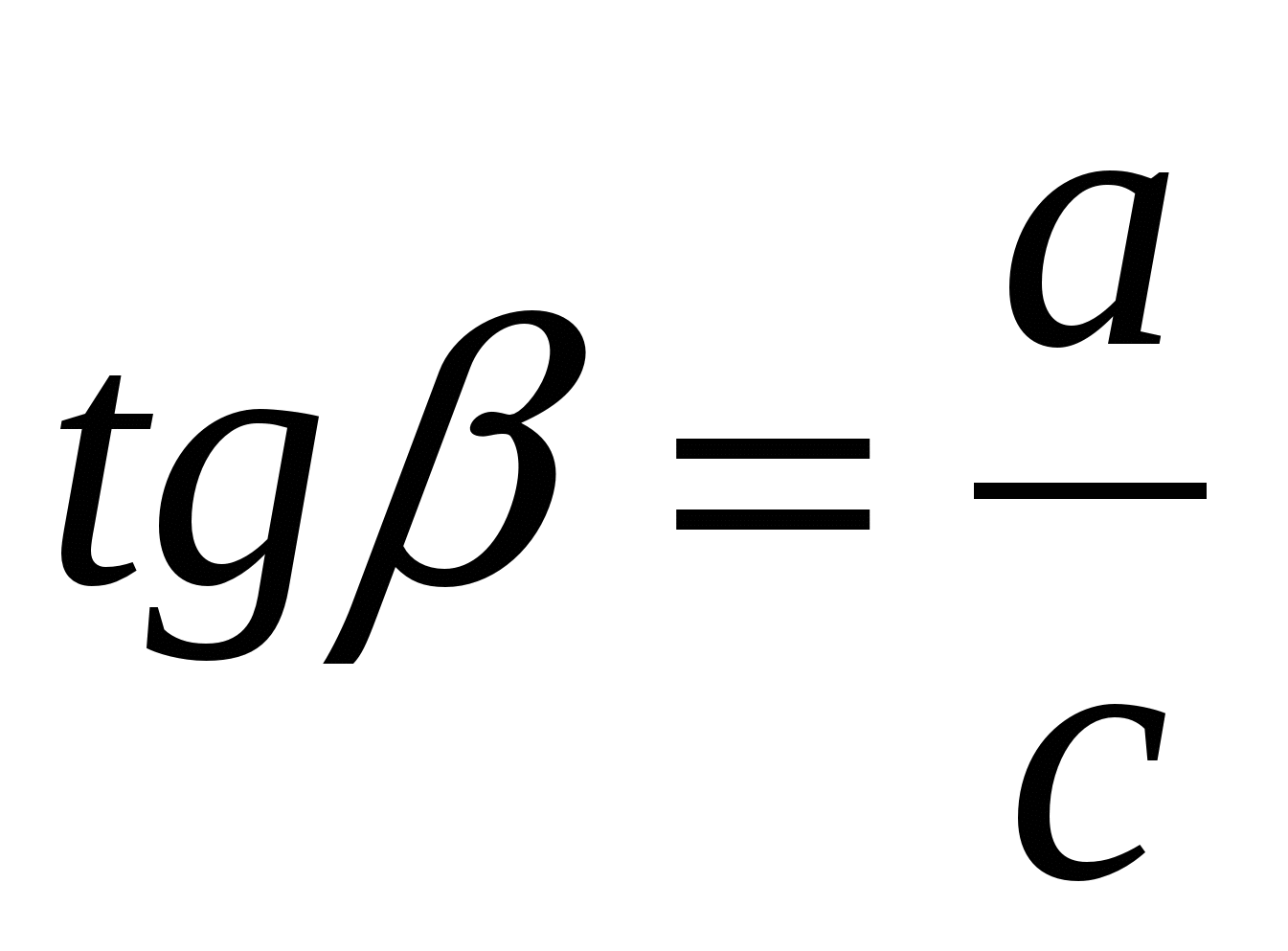 ; в)
; в) 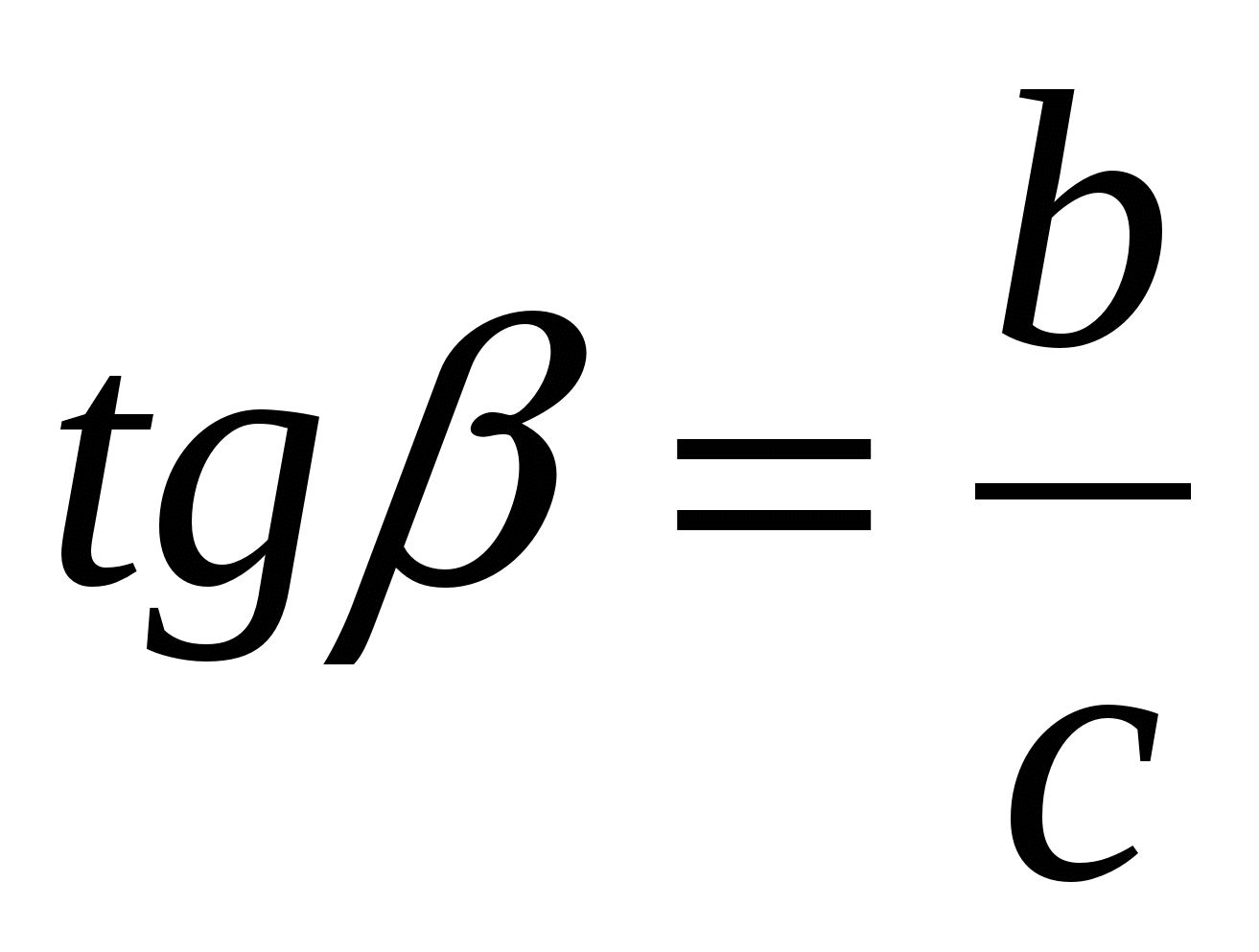 ; г)
; г) 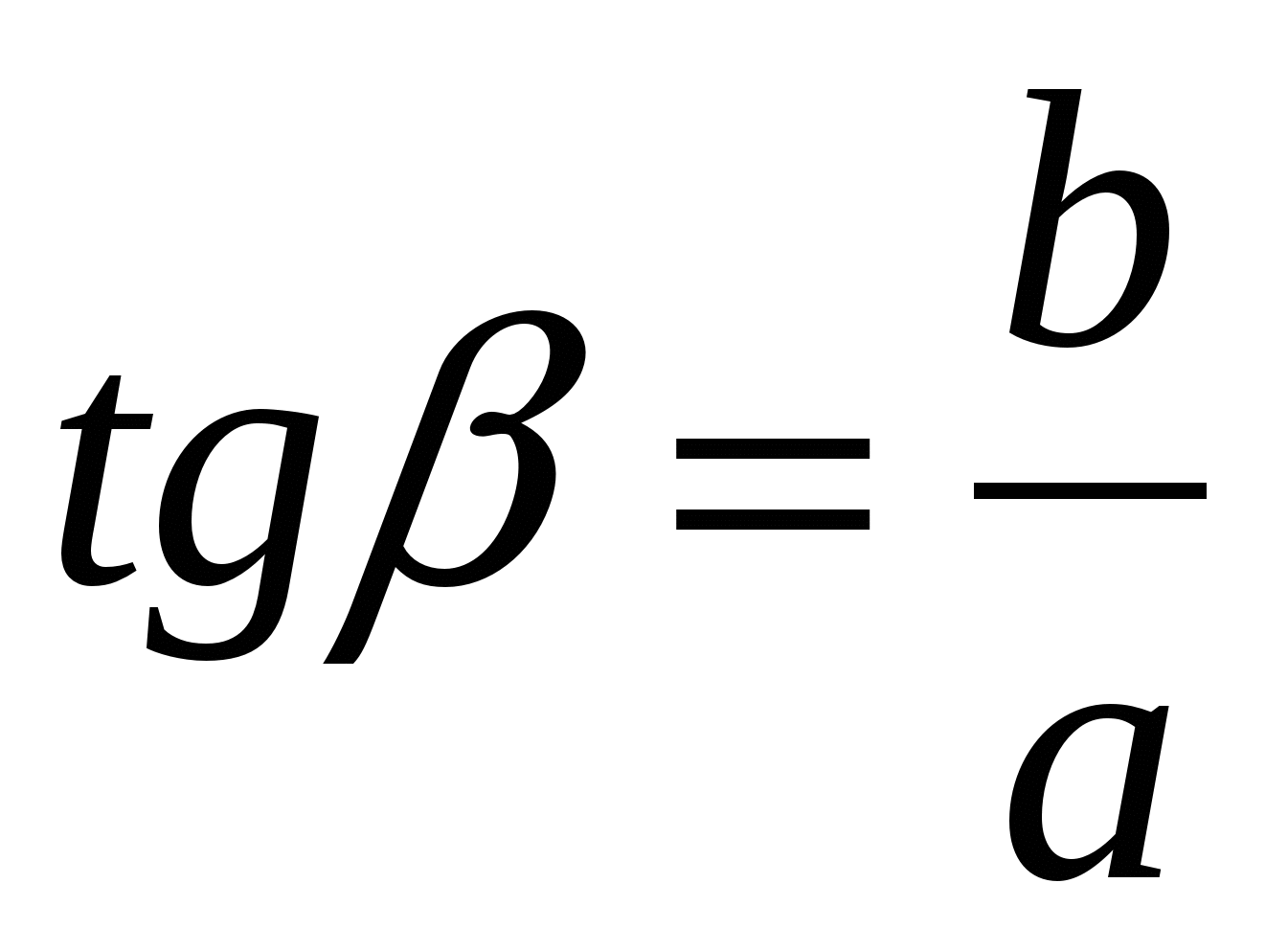 .
.
4) ЗАДАЧИ:
1) В треугольнике АВС, угол С=90, cos А=0,4. Найти sin А.
2) Боковые стороны прямоугольной трапеции равны 15 м и 9 м. Найдите косинус острого угла трапеции.
Билет №6
1) Верно ли высказывание:
а) Тангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему;
б) Катет прямоугольного треугольника равен половине гипотенузы;
в) Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему;
г) Синусом острого угла прямоугольного треугольника называется отношение: противолежащего катета к гипотенузе;
д) Гипотенуза прямоугольного треугольника равна сумме катетов.
2) Докажите теорему:
Сформулируйте и докажите утверждения о пропорциональных отрезках в прямоугольных треугольнике (одно на выбор).
3) ОТВЕТ ПО РИСУНКУ:
Используя рисунок, выбери правильный ответ:
а) 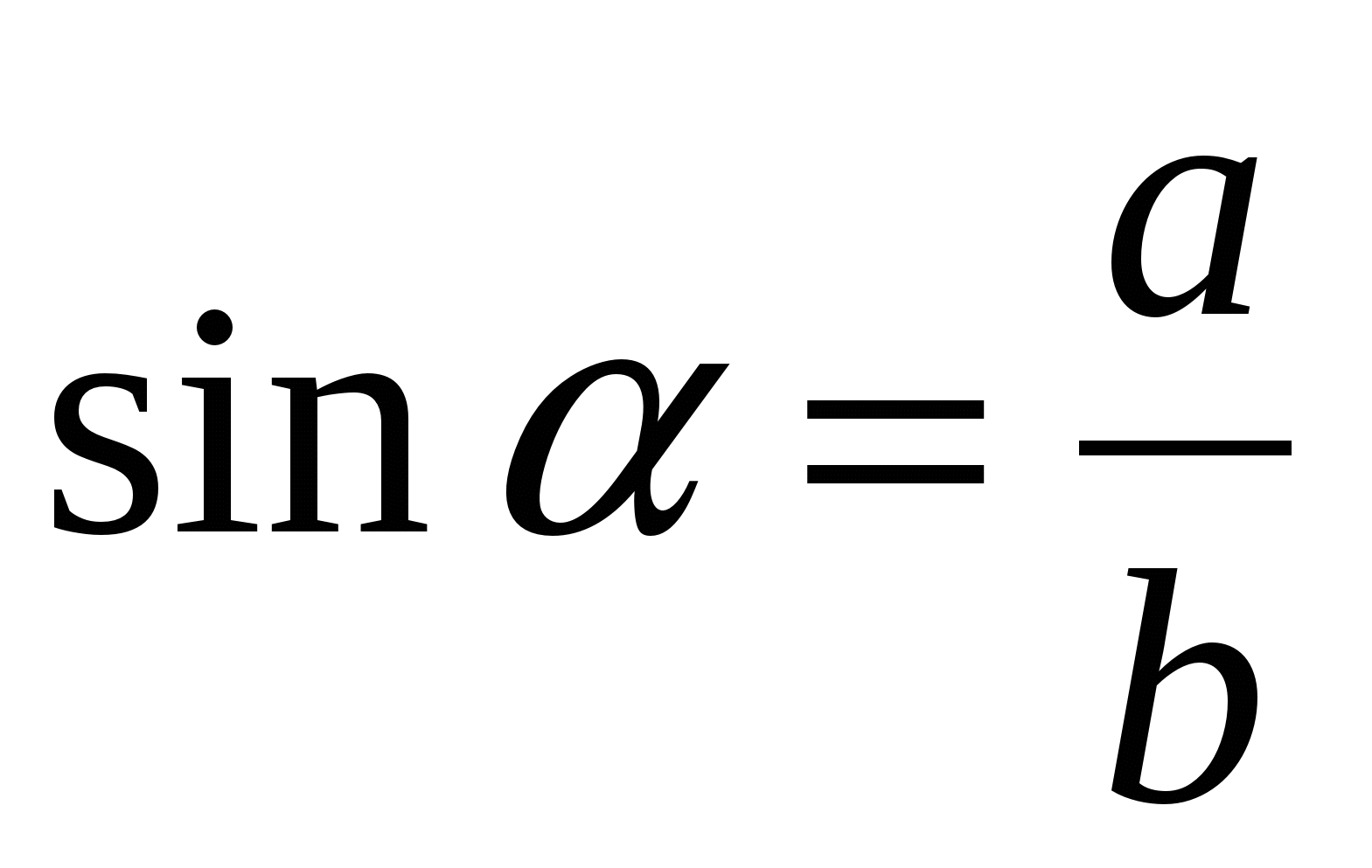 ; б)
; б) 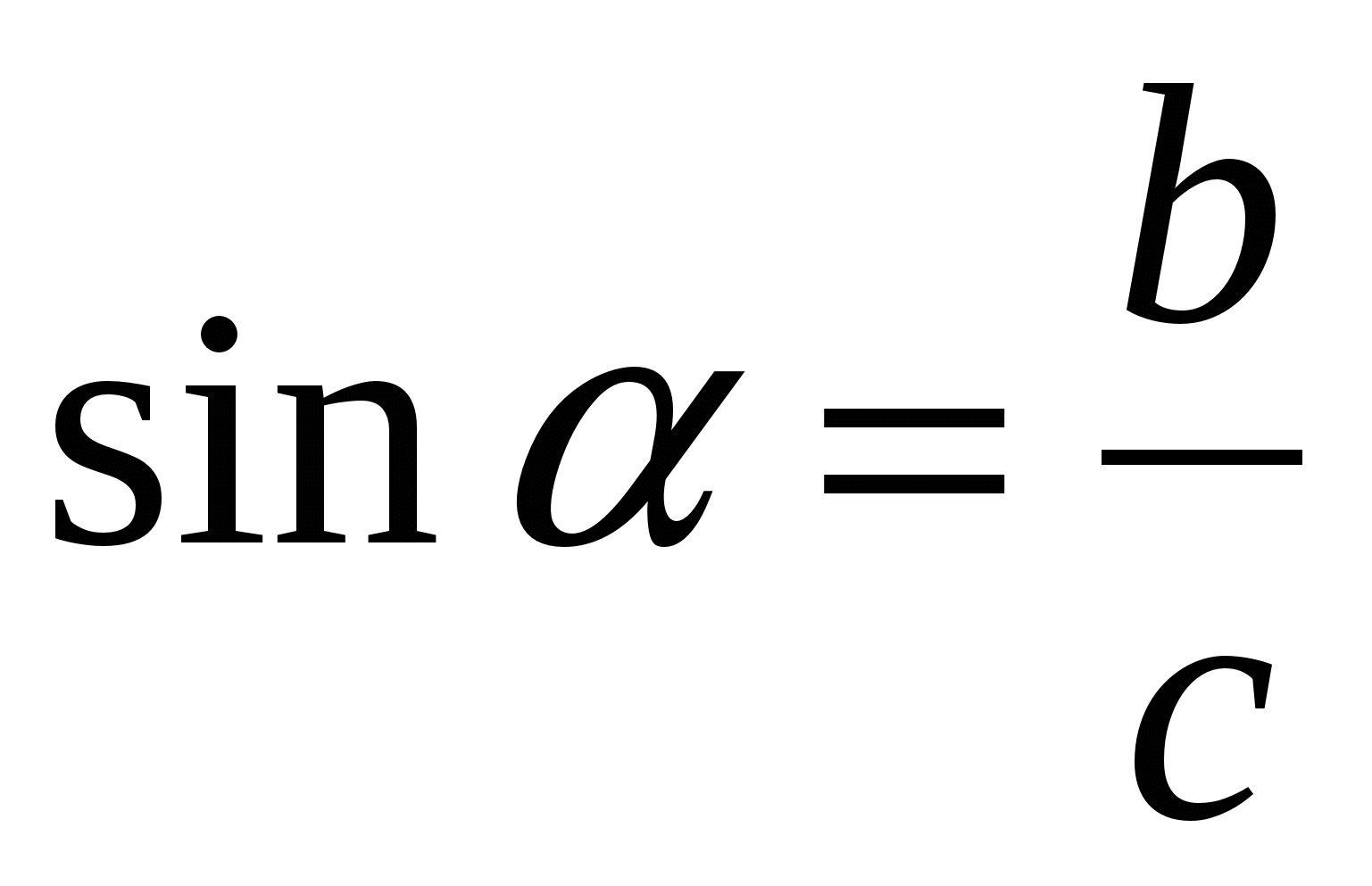 ; в)
; в) 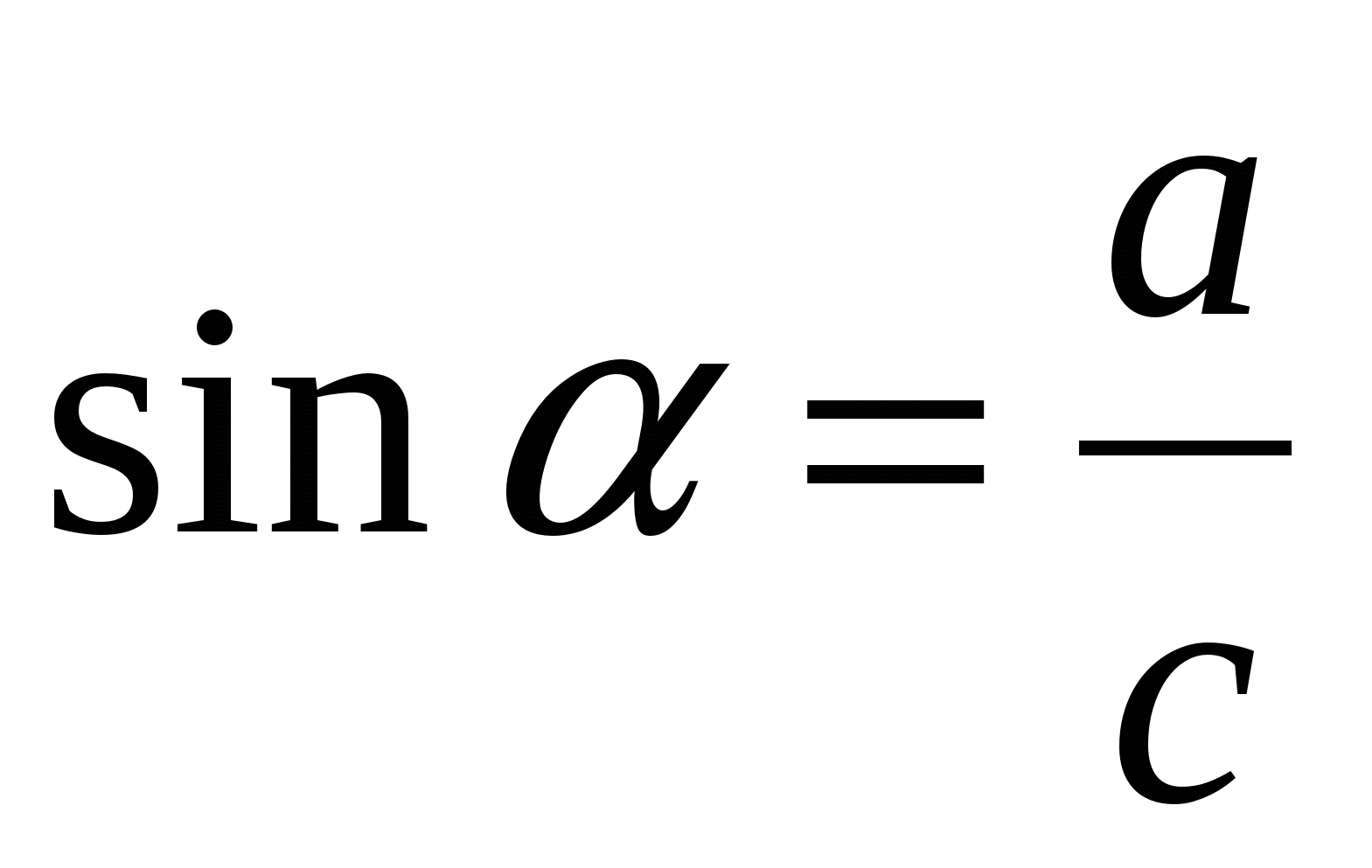 ; г)
; г) 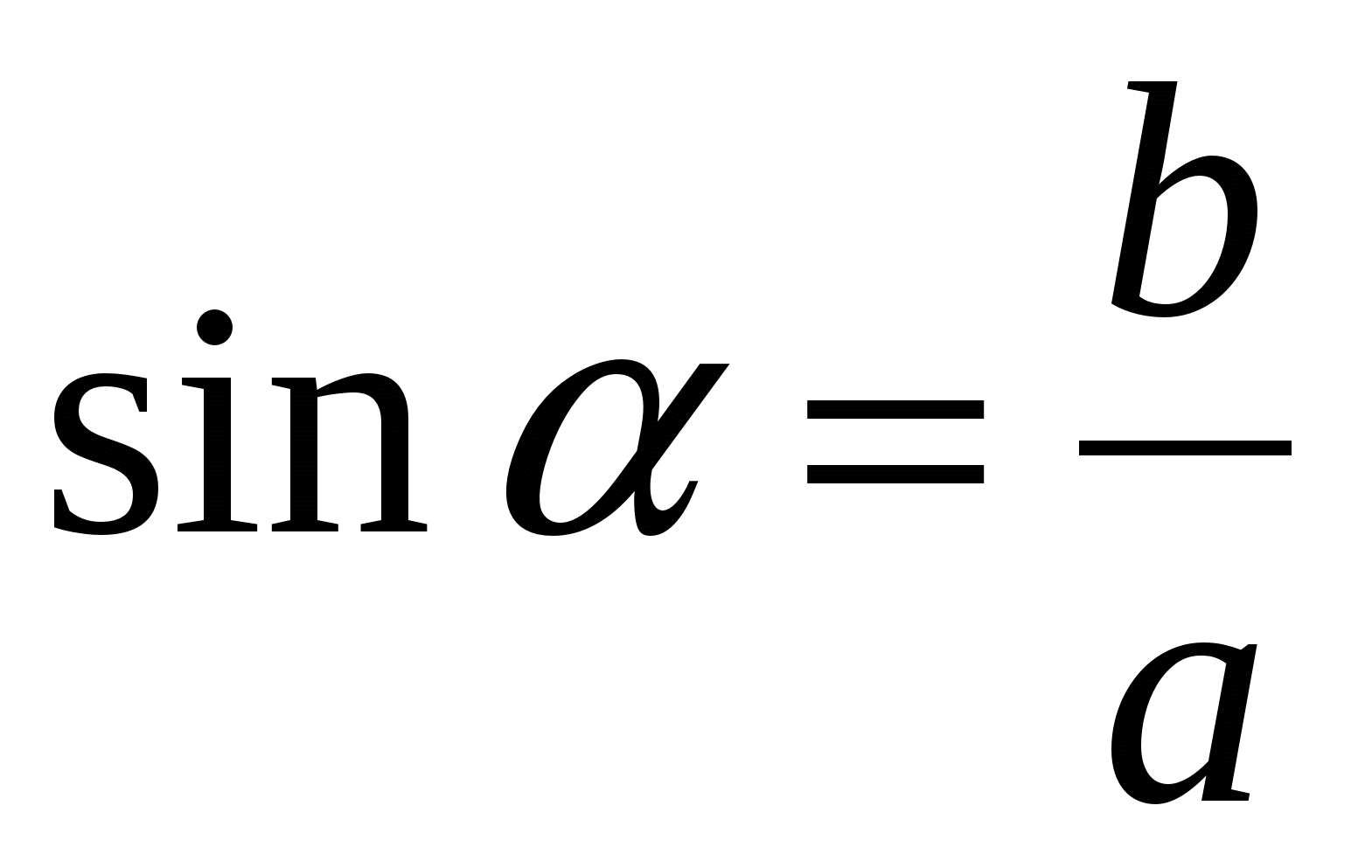 .
.
4) ЗАДАЧИ:
1) В треугольнике АВС, А С= ВС=10, АВ = 14. Найти cos А.
2) В равнобедренной трапеции АВСD большее основание АD=b, угол А равен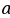 . Диагональ АС перпендикулярна стороне СD. Найти СD, ВС, периметр и площадь трапеции.
. Диагональ АС перпендикулярна стороне СD. Найти СD, ВС, периметр и площадь трапеции.


















