Задания и упражнения, направленные на формирование познавательных универсальных учебных действий при изучении темы «Формулы сокращенного умножения» в 7 классе
Одной из важных задач основного общего образования является задача развития познавательных универсальных учебных действий учащихся. В её основу входят формирование и развитие у обучающегося общеучебных и логических действий, действий постановки и решения проблем.
Материал, представленный в этой работе, включает в себя разнообразные задания, направленные на формирование у школьников познавательных универсальных учебных действий при изучении темы «Формулы сокращённого умножения» на уроках алгебры в 7 классе.
1. Найдите целые выражения среди выражений:
3х +7у; 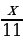 ;
; 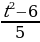 ; 10х + (2х – 3у)(х – у);
; 10х + (2х – 3у)(х – у);
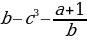 ;
; 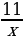 ;
; 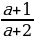 ;
; 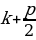 ; а3.
; а3.
2. Сформулируйте задание для каждого выражения и выполните его:
1) (2а – в)(2а + в) + (в – с)(в + с) + (с – 2а)(с + 2а).
2) х2(х – 4) – (х – 4).
3) (3а + 7b)2 – (9а – 5b)2.
4) (692 – 31 ∙ 31) : 19.
5) а(а – 2) – 5а + 10.
6) 5 а2 + 10аb + 5b2.
7) у 4 – 8 у 2 +16 .
8) (а – 8)(а + 4) – 2а(5 – а).
9) (а – х)2 – (а + х)2
10) (а+(в + с))2
3. Среди данных выражений, найдите равные пары:
(2х – у)2;
2(2х – у) 2;
4(2х – у) 2;
(4х – 2у) 2;
0,5(4х – 2у) 2.
4. Какие из следующих многочленов квадраты?
а2 + 4а + 4; а2 + 12а + 9;
х4 + 6 х2 у2 + 9 у2; а2 –10 а в2 + 25в4;
4 а х2 – 6а + 16; х2 + 18х2 + 9.
5. Вычислите:
1. (2 – 1)(2 + 1)(22 + 1) (24 + 1) (28 + 1) (216 + 1) – 232.
2. (1 – 3)(3 + 1)(32 + 1) (34 + 1) (38 + 1) (316 + 1) + 332.
6. Продолжите предложение.
Разложить многочлен на множители это значит...
Способы разложения многочлена на множители:
Метод разложения на множители используется:
7. Объясните каждый шаг решения уравнения:
1) x3 – 4x = 0
x(x2 – 4)= 0
x(x – 2)(x + 2) = 0
x = 0 или x – 2 = 0 или x + 2 = 0
x = 2 x = –2
Ответ: 0; 2; –2.
2) x3 – 2x2 – x + 2 = 0
x2(x – 2) – (x – 2) = 0
(x – 2)(x2 – 1) = 0
(x – 2)(x + 1)(x – 1) = 0
x – 2 = 0 или x + 1 = 0 или x – 1 = 0
x =2 x = –1 x = 1
Ответ: 2; –1; 1.
8. Решите уравнения и объясните каждый шаг решения уравнения:
а) 49x2 – 42x + 9 = 0;
б) x2+ 6x – 7 = 0;
в) x4+ 4y4 = 0
9. Найдите значения числовых выражений, объяснив, какой способ разложения на множители использовали:
45 · 93 + 45 · 7 =
712 + 2 · 71 · 29 + 292 =
25 · 59 + 25 · 41 + 52 · 13 – 52 · 12 =
599 · 601 =
10. Составьте вопросы для зачета по теме «Преобразование целого выражения в многочлен. Разложение многочлена на множители.»
11. Ответьте на вопросы:
Можно ли разложить по формуле сокращенного умножения трехчлен х² – 4х + 1?
Верно ли, что х² + у² = (х + у)(х – у)?
Верно ли, что (х – у) = у – х?
Верно ли, что (4 – х)² = (х – 4)²?
Верно ли, что 49х² – 28х +16 = (7х – 4)²?
Верно ли, что 1 – 9х³ = (1 – 3х)(1 + 3х)?
Верно ли, что 5a – 5b + ха – хb = (5 + х)(а – b)?
12. Найдите ошибку и исправьте ее:
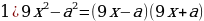 ;
;
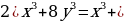
3) 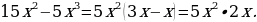
13. Рассмотрите два способа разложения на множители двучлена
х4 – х2:
х2 – х4 = (х – х2) (х + х2) = х (1 – х) ·х (1 + х) = х2 (1 – х) (1 + х);
х2 – х4 = х2 (1 – х2) = х2(1 – х)(1 + х).
Какой из способов вам больше нравится и почему?
14. Изучите задания на сравнение значения выражения с нулём:
1) x2 + 10 0,
т.к. x2 ≥ 0, 10 0.
2) –2x2 – 5
т.к. –2x2 ≤ 0, –5
3) x2 – 16x + 64 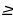 0,
0,
т.к. (x – 8)2 ≥ 0
4) –x2 – 4x – 4 и 0
–(x2 + 4x + 4) и 0
–(x + 2)2 ≤ 0, значит –x2 – 4x – 4 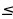 0.
0.
Сравните:
а) –x2 – 1 и 0, б) 7x2 + 9 и 0, в) x2 + 6x +10 и 0.
15. Изучите ещё один способ разложения многочлена на множители.
Разложите на множители 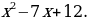
1) Дан многочлен стандартного вида.
2) Степень данного многочлена вторая.
3) Выполним умножение:
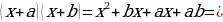
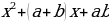 .
.
Таким образом, 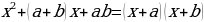 .
.
Проведем аналогию с данным многочленом:
a + b = –7; ab = 12.
Попробуем подобрать такие числа, чтобы при сложении они давали –7, а при умножении 12. В нашем случае это числа – 3 и – 4.
Тогда наш многочлен разложится на множители:
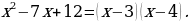
Разложите этим способом многочлен на множители:
1) 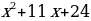 ; 2)
; 2) 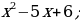 3)
3) 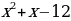 .
.






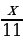 ;
; 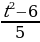 ; 10х + (2х – 3у)(х – у);
; 10х + (2х – 3у)(х – у); 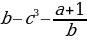 ;
; 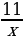 ;
; 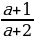 ;
; 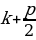 ; а3.
; а3. 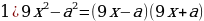 ;
;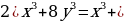
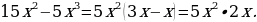
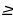 0,
0, 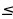 0.
0. 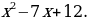
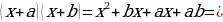
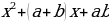 .
.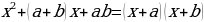 .
.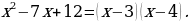
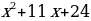 ; 2)
; 2) 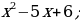 3)
3) 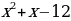 .
.









