Структура экзаменационной работы оп математике
Часть 1
Вычисления с помощью свойств тригонометрических величин.
Вычисления с помощью основных тригонометрических тождеств.
Вычисления с помощью формул, выражающих свойства степеней.
Вычисления с помощью формул, выражающих свойства логарифмов.
Простое показательное уравнение.
Простое логарифмическое уравнение.
Параллельность в пространстве.
Перпендикулярность в пространстве.
Вычисления в многогранниках.
Вычисления в телах вращения
Часть 2
Решение тригонометрического уравнения с выбором решений
Решение показательного уравнения
Решение логарифмического уравнения
Вычисление площади поверхности или объёма многогранника
Вычисление площади поверхности или объёма тела вращения
Демонстрационный вариант
Часть 1
1. Вычислите 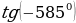 .
.
2. Найдите 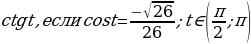 .
.
3. Найдите значение выражения 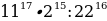 .
.
4. Найдите значение выражения 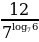 .
.
5. Решите уравнение 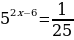 .
.
6. Решите уравнение 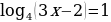 .
.
7. Сторона АВ треугольника АВС параллельна плоскости 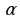 , стороны АС и ВС пересекают плоскость
, стороны АС и ВС пересекают плоскость 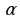 соответственно в точках М и К. Найдите длину отрезка АВ, если АМ : МС=3 : 5, МК=10 см.
соответственно в точках М и К. Найдите длину отрезка АВ, если АМ : МС=3 : 5, МК=10 см.
8. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
9. В прямоугольном параллелепипеде длины непараллельных рёбер равны 24 см, 3 см, 12 см. Найдите длину диагонали параллелепипеда.
10. В цилиндре площадь боковой поверхности равна 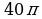 см2, диаметр основания равен 8 см. Найдите высоту цилиндра.
см2, диаметр основания равен 8 см. Найдите высоту цилиндра.
Часть 2
11. Найдите все решения уравнения 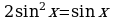 , принадлежащие отрезку
, принадлежащие отрезку 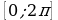 .
.
12. Решите уравнение 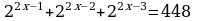 .
.
13. Решите уравнение 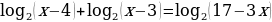
14. Высота боковой грани правильной четырёхугольной пирамиды равна 16 см, а боковое ребро - 20 см. Найдите площадь боковой поверхности пирамиды.
15. Квадрат со стороной 8 см вращается около прямой, проходящей через вершину параллельно диагонали, не проходящей через эту вершину. Найдите объём тела вращения.
Ответы к демонстрационному варианту
| Задания | Ответы |
| 1 | -1 |
| 2 | -0,2 |
| 3 | 5,5 |
| 4 | 2 |
| 5 | 2 |
| 6 | 2 |
| 7 | 16 |
| 8 | 9 |
| 9 | 27 |
| 10 | 5 |
| 11 | 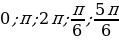
|
| 12 | 4,5 |
| 13 | 5 |
| 14 | 768 |
| 15 | 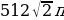
|
Решение демонстрационного варианта
Воспользуемся нечётностью и периодичностью тангенса.
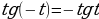
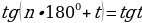 , n- целое число.
, n- целое число.
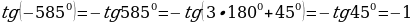
Ответ: 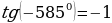
2. По определению котангенс — это отношение косинуса к синусу
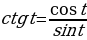
Для нахождения синуса воспользуемся основным тригонометрическим тождеством
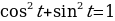
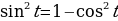
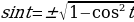
Т.к. 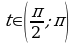 , т.е. принадлежит 2 четверти, то синус будет положительный:
, т.е. принадлежит 2 четверти, то синус будет положительный:
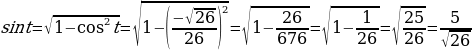
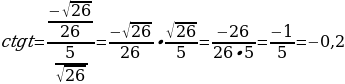
Ответ: 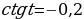
3. 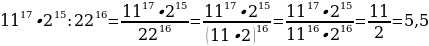
Использовали формулы:
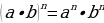
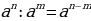
Ответ: 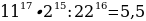
Используем основное логарифмическое тождество
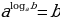
Значит, 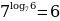
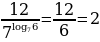
Ответ: 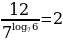
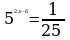
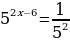
Воспользуемся определением степени с отрицательным показателем 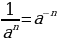 .
.
Получаем
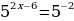
Две степени равны, если у них равны основания и показатели степеней. В уравнении основания степеней одинаковые, значит нужно приравнять показатели степеней.
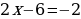
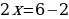
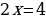
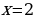
Ответ: 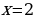
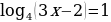
Простое логарифмическое уравнение решается по определению логарифма
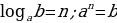
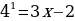
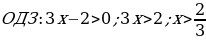
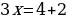
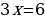
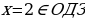
Ответ: 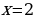
7.
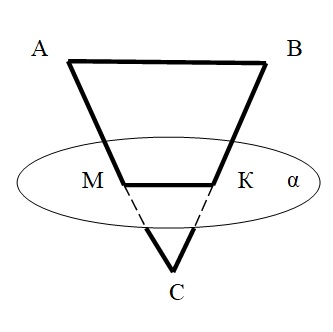
Построим прямую через точки М и К (по аксиоме планиметрии: «Через две точки проходит единственная прямая»). По условию прямая АВ параллельна плоскости α, значит, она параллельна прямой МК, лежащей в этой плоскости.
У нас получилось два подобных треугольника: АВС и МКС (треугольники подобны по двум сторонам и углу между ними).
У подобных треугольников отношение сторон одинаково.
Составим это отношение:
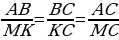
Из трёх отношений выбираем два, чтобы получилась пропорция.
Выбираем первую дробь, потому что она содержит неизвестный отрезок АВ. Выбираем третью дробь, потому что она содержит отрезок МС, о котором также говорится в условии:
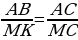
По правилу «креста» выражаем неизвестный отрезок АВ.
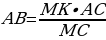
Теперь в эту формулу подставляем численные данные.
МК=10 (см) по условию.
Из отношения АМ : МС=3 : 5 делаем вывод, что отрезок АМ состоит из трёх частей от длины отрезка АС, а отрезок МС состоит из пяти частей от длины отрезка АС, значит, весь отрезок АС состоит из восьми равных частей. Пусть длина каждой этой части равна х, тогда отрезок МС=5х, а отрезок АС=8х. Подставим всё в формулу
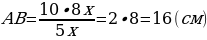
Ответ: АВ=16 (см)
8.


A





α



C
D
B
Отрезок АВ находится в двух прямоугольных треугольниках: Δ АВС и Δ ABD. АВ- это общий катет этих треугольников.
Воспользуемся теоремой Пифагора и выразим АВ из каждого треугольника:
АВ2=АС2-СВ2 (выразили из ΔАВС)
АВ2=АD2-BD2 (из Δ ABD).
Получили два равенства, у которых левые части равны, значит, правые тоже должны быть равны.
Приравняем правые части равенств.
АС2 - СВ2=АD2 - BD2 (1)
АС и АD — это наклонные, по условию задачи их длины известны: АС=23 см, АD=33 см.
Проекции наклонных - СВ и BD.
Длины отрезков СВ и BD неизвестны.
Мы знаем, что у большей наклонной будет большая проекция.
По условию задачи проекции наклонных относятся как 2:3.
Это значит, что отрезок ВС состоит из двух частей, отрезок BD состоит из трёх частей.
Если каждую часть обозначить за х, то получаем, что ВС=2х, BD=3x.
Подставим всё в формулу (1):
232-(2х)2=333-(3х)2
529-4х2=1089-9х2
5х2=560
х2=112
х=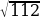
Тогда
АВ2 =АС2 - СВ2 =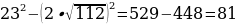
АВ = 9 (см)
Ответ: АВ=9 (см)


C1
B1
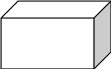
9. 




А1
D1


С
В




D
А
Применим свойство прямоугольного параллелепипеда: «Квадрат любой диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений».
Измерения прямоугольного параллелепипеда — это длины непараллельных рёбер (т.е. длина, ширина, высота).
Рёбра АА1, АD и АВ между собой не параллельны, значит, они являются линейными размерами параллелепипеда.
Пусть АА1=24 см, AD=3 см, АВ=12 см.
Отрезок В1D соединяет вершины параллелепипеда, не лежащие в одной грани, значит, он является диагональю параллелепипеда.
Тогда получаем
B1D2=AA12+AD2+AB2
B1D2=242+33+12=576+9+144=729
B1D=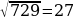 (см)
(см)
Ответ: B1D=27 см
 10.
10.

Боковая поверхность цилиндра равна: 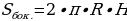
По условию, боковая поверхность равна 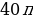 см2.
см2.
Если диаметр равен 8 см, то радиус равен 4 см.
Подставим всё в формулу боковой поверхности, получим
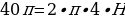
Выразим высоту: 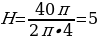
Ответ: H=5 см
11.
1) Найдем все решения уравнения
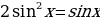
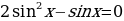
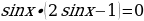
Произведение равно нулю, если один из множителей равен нулю, значит:
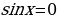 или
или 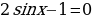
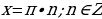
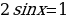
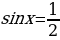
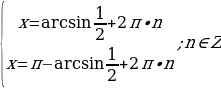
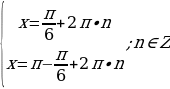
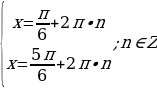
2) Нужно выбрать решения, принадлежащие промежутку 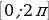 .
.
На оси ординат отметим значение синуса, равное 0 и 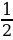 .
.
Через эти точки проведём прямые, параллельные оси абсцисс.
Получим частные решения x1, x2, x3, x4, x5.
Определим их, двигаясь по окружности в положительном направлении (т.е. против часовой стрелки).

y

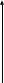






x5



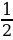
x2
x3








x
0
x1
x4
x1=0
x2 =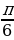
x3 =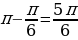
x4 = π
x5 = 2π
Ответ: x1=0, x2 =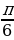 , x3 =
, x3 =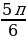 , x4 = π, x5 = 2π.
, x4 = π, x5 = 2π.
12. Если в показательном уравнении у степеней одинаковые основания, а показатели степеней отличаются на какое- то число, то это уравнение нужно решать способом вынесения за скобку степени с наименьшим показателем.
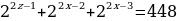
В нашем случае 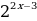 - степень с наименьшим показателем, её вынесем за скобку. Вынесение за скобку равносильно делению. При делении степеней с одинаковыми основаниями и разными показателями основание остаётся прежним, а показатели вычитаются. Получаем
- степень с наименьшим показателем, её вынесем за скобку. Вынесение за скобку равносильно делению. При делении степеней с одинаковыми основаниями и разными показателями основание остаётся прежним, а показатели вычитаются. Получаем
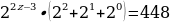
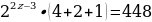
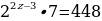
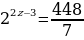
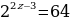
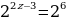
Если две степени равны, то у них равны и основания, и показатели.
Приравняем показатели степеней.
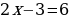
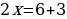
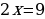
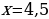
Ответ: x=4,5
13. 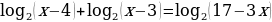
Найдем область допустимых значений уравнения
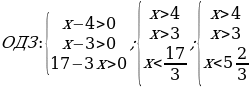
В левой части уравнения воспользуемся свойством логарифма:
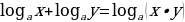
Получаем
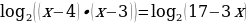
Логарифмы равны, если у них равны основания и логарифмируемые выражения.
В данном уравнении основания логарифмов одинаковые, значит нужно приравнять логарифмируемые выражения:
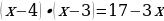
Раскрываем скобки в левой части равенства
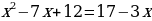
Из правой части равенства все слагаемые перенесём в левую часть и приведём подобные.
Получается приведённое квадратное уравнение
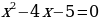
Воспользуемся теоремой Виета: 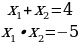 ;
; 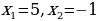
Т.к. x2 не удовлетворяет ОДЗ, то ответом будет только x1=5.
Ответ: 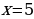

S
14. 




C
B







M
O




D
A
Боковая поверхность правильной пирамиды равна половине произведения периметра основания на апофему (апофема - это высота боковой грани правильной пирамиды).
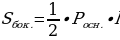 ( l- апофема)
( l- апофема)
По условию апофема равна 16 см. Нужно найти периметр основания. В основании правильной четырёхугольной пирамиды лежит квадрат. Периметр квадрата:
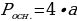 (a-сторона квадрата).
(a-сторона квадрата).






S
C
M
Для того чтобы найти сторону квадрата рассмотрим треугольник SMC. Этот треугольник прямоугольный. В нём известны две стороны. Значит, для нахождения третьей стороны нужно воспользоваться теоремой Пифагора.
SC2 = SM2+MC2
MC2 = SC2 - SM2
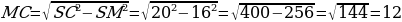 (см)
(см)
Точка М - середина отрезка DC (все боковые грани правильной пирамиды- равнобедренные треугольники, в равнобедренном треугольнике высота – это и биссектриса, и медиана), значит DC=24 (см).
Периметр основания Pосн.=96 (см)
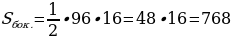 (см2).
(см2).
Ответ: 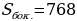 (см2)
(см2)
 15.
15.













M
B





O
C
A

D

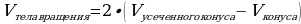
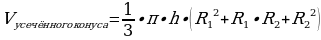
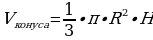
h- высота усечённого конуса; h=MC =BO
R1-радиус верхнего основания усечённого конуса; R1=BM
R2-радиус нижнего основания усечённого конуса ; R2=AC
R- радиус конуса; Rк=BM
H- высота конуса; Hк=MC
Высота усечённого конуса h равна половине диагонали BD квадрата ABCD.
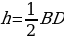
Из прямоугольного треугольника BAD найдём по теореме Пифагора BD.
BD2=AB2+AD2=82+82=128
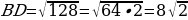 ( см)
( см)
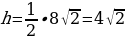 (см)
(см)
H=MC=BO=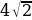 (см)
(см)
R1=MB=OC= 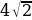 (см)
(см)
R2=CA=BD=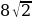 (см)
(см)
R=MB=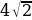 (см)
(см)
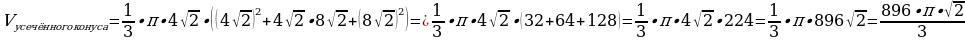
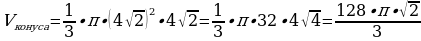
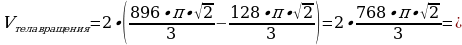
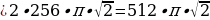 (см3)
(см3)
Ответ: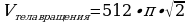 (см3).
(см3).






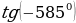 .
.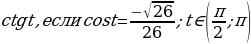 .
.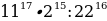 .
. 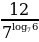 .
.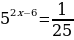 .
. 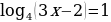 .
. 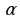 , стороны АС и ВС пересекают плоскость
, стороны АС и ВС пересекают плоскость 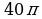 см2, диаметр основания равен 8 см. Найдите высоту цилиндра.
см2, диаметр основания равен 8 см. Найдите высоту цилиндра.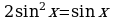 , принадлежащие отрезку
, принадлежащие отрезку 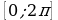 .
.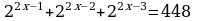 .
.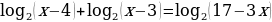
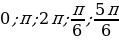
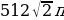
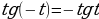
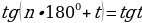 , n- целое число.
, n- целое число.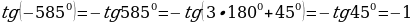
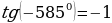
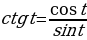
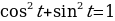
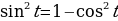
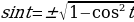
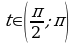 , т.е. принадлежит 2 четверти, то синус будет положительный:
, т.е. принадлежит 2 четверти, то синус будет положительный: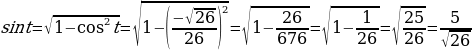
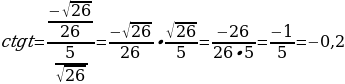
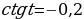
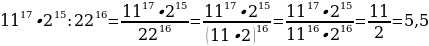
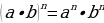
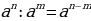
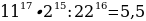
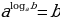
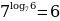
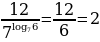
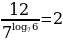
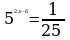
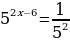
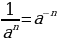 .
.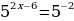
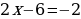
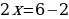
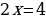
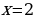
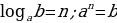
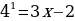
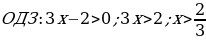
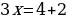
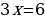
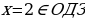

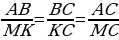
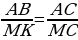
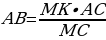
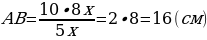










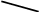
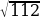
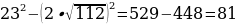













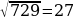 (см)
(см) 10.
10. 
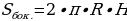
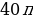 см2.
см2. 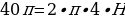
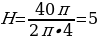
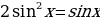
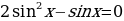
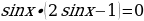
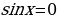 или
или 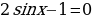
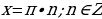
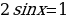
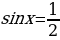
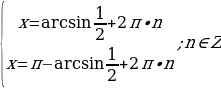
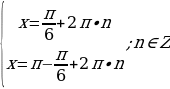
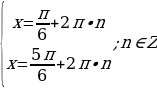
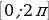 .
.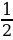 .
. 

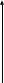











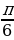
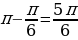
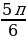 , x4 = π, x5 = 2π.
, x4 = π, x5 = 2π.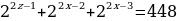
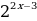 - степень с наименьшим показателем, её вынесем за скобку. Вынесение за скобку равносильно делению. При делении степеней с одинаковыми основаниями и разными показателями основание остаётся прежним, а показатели вычитаются. Получаем
- степень с наименьшим показателем, её вынесем за скобку. Вынесение за скобку равносильно делению. При делении степеней с одинаковыми основаниями и разными показателями основание остаётся прежним, а показатели вычитаются. Получаем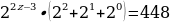
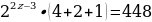
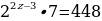
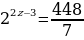
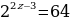
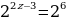
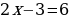
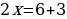
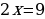
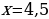
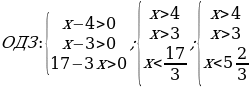
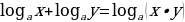
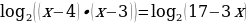
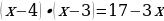
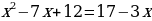
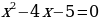
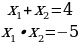 ;
; 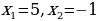
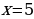













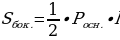 ( l- апофема)
( l- апофема)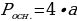 (a-сторона квадрата).
(a-сторона квадрата).



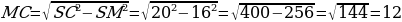 (см)
(см)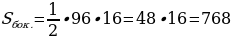 (см2).
(см2).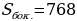 (см2)
(см2) 15.
15. 

















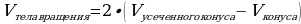
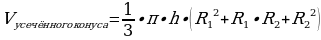
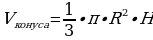
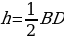
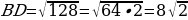 ( см)
( см)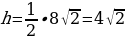 (см)
(см)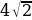 (см)
(см)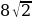 (см)
(см)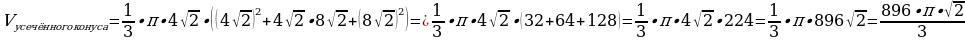
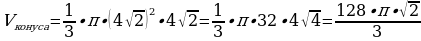
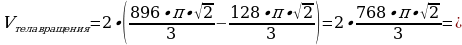
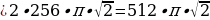 (см3)
(см3)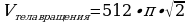 (см3).
(см3).









