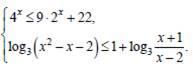Диагностические материалы по математике к ЕГЭ

В1. Билет на автобус стоит 15 рублей. Какое максимальное число билетов можно будет купить на 100 рублей после повышения цены билета на 20%?

Ответ: 5

Решение

Процент - сотая часть чего-либо. То есть 20% - двадцать сотых, или одна пятая от чего-то. Есть три способа решения этой задачи, я приведу самый простой, на мой взгляд:

Переведем задачу на язык процентов. Билет стоил 100%, а после подорожания стал стоить на 20% больше - то есть 120%. 120% - это сто двадцать сотых числа - или 1,2. То есть новая цена билета:

15*1,2=18 (руб.)

То есть на 100 рублей можно купить: 100/18=5,55 (но так как число билетов - целое число. то ответ - 5 билетов).

Ответ: 5

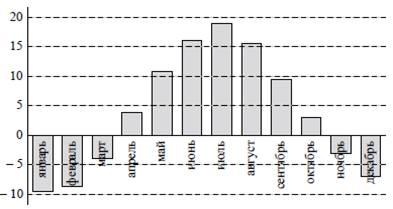
В2. На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Ярославле по результатам многолетних наблюдений. Найдите по диаграмме количество месяцев, когда средняя температура в Ярославле была отрицательной.

Ответ: 5

Решение

Здесь на диаграмме мы должны искать все месяцы, где столбик находится в отрицательной зоне. Таких месяцев ровно пять - три первых, и два последних. Ответ: 5

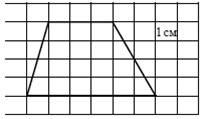
В3. Найдите площадь четырёхугольника,изображённого на клетчатой бумаге сразмером клетки 1 см · 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.

Ответ: 18

Решение

Площадь трапеции равна полусумме оснований на высоту. Высота равна четырем клеточкам (4 см.), основания равны 6 см. и 3 см. Производим несложные вычисления:

Полусумма оснований: (6+3)/2=4,5 см.

Искомая площадь равна: 4,5*4=18 см. квадратных.

Ответ: 18

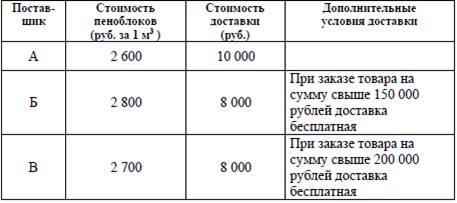
В4. Строительная фирма планирует купить 70 м³ пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?

Ответ: 192000

Решение

Рассчитаем общую сумму заказа при работе с каждым поставщиком. Для этого стоимость пеноблоков за кубометр умножаем на необходимое количество кубометров пеноблоков, а затем к полученной сумме надо прибавить сумму доставки (если нет специального предложения о бесплатной доставке).

Поставщик А (сумма без доставки): 2600 * 70 = 182000 (руб)

Дополнительных условий поставки нет, поэтому конечная сумма равна: 182000+10000=192000 (руб)

Поставщик Б (сумма без доставки): 2800 * 70 = 196000 (руб)

Сумма поставки превышает 150000 руб., поэтому данная сумма окончательна (доставка бесплатна)

Поставщик B (сумма без доставки): 2700 * 70 = 189000 (руб)

-Сумма поставки не превышает 200000 руб., поэтому конечная сумма равна: 189000+8000=197000 (руб)

У поставщика А самые привлекательные условия.

Ответ: 192000

В5. Найдите корень уравнения log₃(x - 3) = 2.

Ответ: 12

Решение

Логарифм числа по основанию определяется как показатель степени х, в которую надо возвести основание a, чтобы получить число b. Обозначается: log_аb=x.

Согласно определению, a^x=b Применим эти знания к данном примеру:

32=x-3
9=x-3
x=12

- По ОДЗ, х-30, данный корень подходит.
Oтвет: 12

В6. Треугольник ABC вписан в окружность с центром O . Найдите угол BOC , если угол BAC равен 32° .

Ответ: 64°

Решение

Вписанный угол — угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность. Центральный угол — угол, образованный двумя радиусами окружности. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.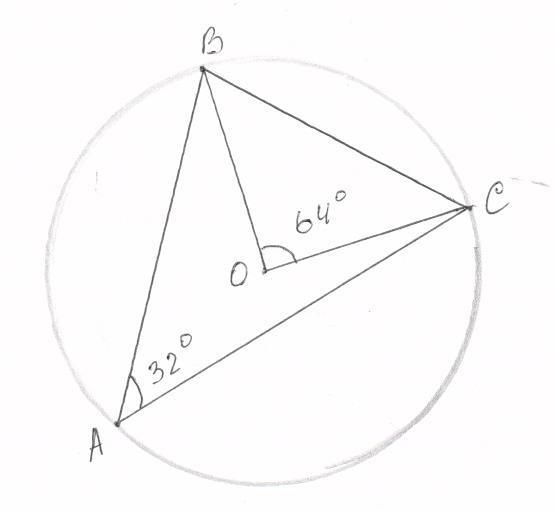

В данном случае оба угла, упомянутые в задаче, опираются на одну и ту же дугу ВС.

Угол ВОС - центральный, так как он образован двумя радиусами окружности. Вершина угла ВАС лежит на окружности, так как треугольник АВС вписан в окружность, а обе стороны данного угла пересекают окружность. Т.е. угол ВАС - вписанный.

Так как вписанный угол равен половине центрального угла, опирающегося на ту же дугу, получаем, что градусная мера угла ВОС составляет 32*2=64 градуса

В7. Найдите sina , если cosa = 0,6 и π a

Ответ: -0.8

Решение

Основное тригонометрическое тождество (ОТТ) гласит: cos2α + sin2α = 1

Выразим квадрат синуса угла из ОТТ и подставим данные из задачи:

sin2α = 1 — 0,62
sin2α = 1—0,36
sin2α = 0,64

А теперь вспомним знаки тригонометрических функций по четвертям: А теперь вспомним знаки тригонометрических функций по четвертям: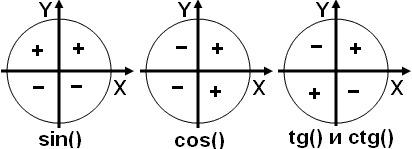

Интервал π

Ответ: — 0,8

В8. На рисунке изображён график функции y = f ( x) и отмечены девять точек на оси абсцисс: x₁, x₂, x₃, ..., x₉ . В скольких из этих точек производная функции f ( x) отрицательна?

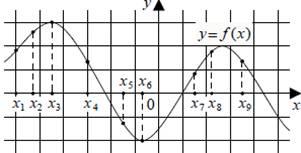
Ответ: 3

Решение

Если касательная возрастающая, то производная будет положительной, а если касательная убывающая, то производная отрицательная.

На рисунке проведены все касательные в указанных точках.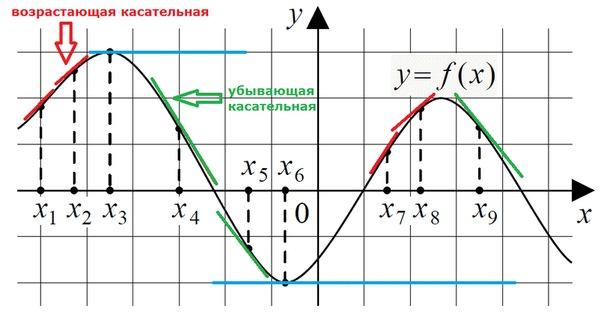

Нас интересуют убывающие касательные, так как искомые производные должны быть отрицательными Таких точек три - касательные к ним отмечены зеленым цветом.

Производная функции y’= tg А , где А - угол наклона касательной к оси абсцисс.

В9. Диагональ AC основания правильной четырёхугольной пирамиды SABCD равна 6.Высота пирамиды SO равна 4. Найдите длину бокового ребра SB .

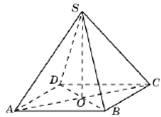
Ответ: 5

Решение

Правильной четырехугольной пирамидой называется такая пирамида, у которой в основании лежит квадрат, а все боковые ребра равны между собо й.

Высота такой пирамиды падает в точку пересечения диагоналей основания.

Диагонали квадрата равны, причем диагонали квадрата делятся точкой пересечения пополам.

Т.е. АС=BD=2*ВО ВО=6/2=3 (см)

Рассмотрим треугольник SOB. Он - прямоугольный. Известны оба катета.

Гипотенуза в прямоугольном треугольнике со сторонами 3 и 4 равна 5 (египетский треугольник). Можно проверить по теореме Пифагора.

То есть SB = 5
Ответ: 5

В10. В сборнике билетов по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет. Найдите вероятность того, что в этом билете не будет вопроса о грибах.

Ответ: 0.92

Решение

Рассмотрим событие: вытянуть вопрос о грибах.

Всего два вопроса о грибах, поэтому всего благоприятных исходов два, а всего исходов 25.

Искомая вероятность равна 2/25=0,08.

Pассмотрим противоположное событие: не вытянуть вопрос о грибах, вытянуть любой другой вопрос

Общая вероятность событий: "вытянуть вопрос о грибах" и "не вытянуть вопрос о грибах" равна 1, потому что других вариантов нет.

Итак, вероятность события "не вытянуть вопрос о грибах" равна: 1-0,08=0,92

Ответ: 0,92

В11. Объём первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м³).

Ответ: 9

Решение

• Переместить

• Закрыть

Объем цилиндра: V=πr²h. Из условия следует, что r₂=(1/2)*r₁. Также из условия следует, что h₂=3*h₁.

Далее следует цепочка несложных преобразований:

V₂=π(r₂)²h₂
V₂=π(0,5*r₁)²*3h₁
V₂=0,25*3*π(r₁)²*h₁
V₂=0,25*3*12
V₂=9

Ответ: 9

В12. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t ) = -5t² +18t , где h –высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров.

Ответ: 2.4

Решение

• Переместить

• Закрыть

Задача сводится к решению неравенства: -5t² +18t≥9

-5t² +18t-9≥0
5t²-18t+9≤0
D=324-180=144
Корень из дискриминанта равен 12
х_1,2=(18±12)/10
Корни: 3 и 0,6

Решим неравенство методом интервалов:

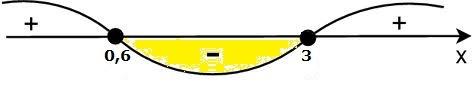
Итак, камень находился на указанной высоте в течение3-0,6=2,4 (сек)
Ответ: 2,4

В13. Весной катер идёт против течения реки в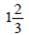 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в1½ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Ответ: 5

Решение

На общую скорость катера влияют два параметра: собственная скорость Vс катера - она постоянна и летом, и весной, а также скорость течения Vтеч: для разных сезонов скорость течения обозначим как Vтв (весной) и Vтл (летом).

Скорость катера по течению: Vc+Vтеч

Скорость катера против течения: Vc-Vтеч

В соответствии с вышесказанным, перепишем условие задачи в виде системы:

(Vc+Vтв)/(Vc-Vтв) = 5/3
(Vc+Vтл)/(Vc-Vтл) = 3/2
Vтл=Vтв-1

(Vc+Vтв)/(Vc-Vтв) = 5/3
(Vc+Vтв-1)/(Vc-Vтв+1) = 3/2
Vтл=Vтв-1

Упростим первое уравнение:

3Vc+3Vтв=5Vc-5Vтв
-2Vc=-8Vтв
Vc=4Vтв

Подставим полученное во второе уравнение и упростим его:

(5Vтв-1)/(3Vтв+1) = 3/2
10Vтв-2=9Vтв+3
Vтв=5

Итак, скорость течения весной равна 5 километров в час.

Ответ: 5

В14. Найдите наибольшее значение функции:

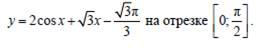
Ответ: 1

Решение

С1. Решите уравнение 6sin² x + cos x - 5 = 0 и найдите корни, принадлежащие отрезку [2π; 3π].

Решение

С2. Сторона основания правильной треугольной призмы ABCA₁B₁C₁ равна 2 , а диагональ боковой грани равна √5 . Найдите угол между плоскостью A₁BC и плоскостью основания призмы.

Решение

С3.Решите систему неравенств: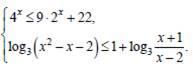

Решение

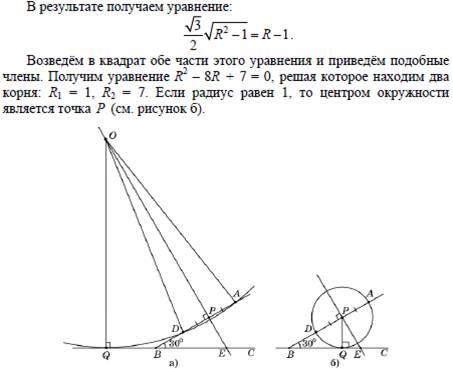
С4. На стороне BA угла ABC , равного 30º, взята такая точка D, что AD = 2 и BD =1. Найдите радиус окружности, проходящей через точки A, D и касающейся прямой BC.

Решение

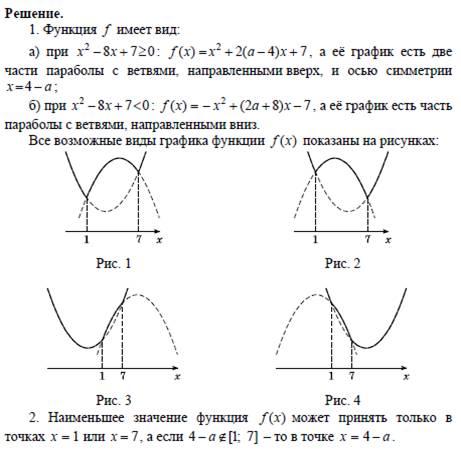
С5. Найдите все значения a , при каждом из которых наименьшее значение функции f (x) = 2ax + | x² - 8x + 7 | больше 1.

Решение

С6. На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно -3 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно -8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?

Решение