Министерство образования и науки Республики Калмыкия
Муниципальное казенное общеобразовательное учреждение
«Цаган-Нурская сош имени Н.М. Санджирова»
Дидактическая разработка
на тему «Корни. Степени. Логарифмы»
Номинация «Дидактическая разработка»
Составитель:
учитель физики и математики
МКОУ «ЦНСОШ им.Н.М. Санджирова»
Борлыкова Галина Дорджиевна
2021 г.
Оглавление.
Аннотация. Введение ………………………………………………. 3
Основная часть. ……………… ……………………………………… 4
Литература ……………………………………………..….…………….. 12
Приложение ……………………………………………………………... 13
Аннотация.
Данная разработка необходима для успешного изучения темы «Корни. Степени. Логарифмы» в системе ООО. Разработка предназначена в помощь педагогу при подборе дидактического материала для изучения данной темы. Цель: использование педагогических технологий в учебном процессе с целью повышения качества знаний, умений и навыков обучающихся.
Введение.
Сейчас все больше и больше говорят об инклюзии. В основу инклюзивного образования положена идеология, которая обеспечивает равное отношение ко всем людям, но создает особые условия для детей, имеющих особые образовательные потребности. Инклюзивное образование - относительно новая область, которая предполагает обучение детей с различными образовательными потребностями и детей с ограниченными возможностями здоровья вместе. До недавнего времени, обучение детей с ОВЗ в общеобразовательной школе носило исключительно индивидуальный характер – домашнее обучение. Обучение детей с ОВЗ в настоящее время стало развиваться. Основным приоритетом инклюзивного образования является то, что все дети, несмотря на свои физические, психические и иные особенности, обучаются вместе со своими сверстниками по месту жительства в массовой общеобразовательной школе, где им оказывается необходимая специальная поддержка. Инклюзивное образование предполагает, что дети с различными особенностями как и любые другие дети должны быть включены в образовательный процесс и одинаковые виды деятельности: коллективные формы обучения и групповое решение задач, использование стратегии коллективного участия – игры, совместные проекты, лабораторные, полевые исследования и т. д., а учреждения образования – создать им для этого соответствующие условия. Дети с разными отклонениями в развитии требуют различных подходов и методик работы для приобретения навыков саморазвития, самосовершенствования, укрепления своего положения в социуме, что предъявляет новые и более высокие требования ко всем педагогам, работающим в школе. Учитель становится координатором инклюзивного процесса в классе в сотрудничестве со всеми участниками воспитательно-образовательного процесса: командой специалистов, администрацией, родителями и учащимися. Для учителя в инклюзивной образовательной среде важно владеть практикой и умениями творчески перерабатывать учебный план для конкретного класса, а также для конкретного ребенка и адаптировать свои методы обучения к особенностям учеников [1].
Не первый учебный год я работаю с детьми с ОВЗ. Стараюсь выбирать методы и технологию обучения, которые приводят к ситуации успеха, как классного коллектива, так и индивидуально каждого обучающегося. В частности отдаю предпочтение технологии УДЕ академика РАО П.М. Эрдниева.
Основная часть.
УДЕ представляет собой систему крупноблочного построения программного материала, согласно которому, рассматривая взаимосвязи и взаимопереходы, следует выделить крупными блоками целостные группы родственных единиц этого содержания. При этом, укрупненная единица определяется не объемом выдаваемой информации, а именно, наличием связей – взаимно обратными мыслительными операциями, комплексами взаимно обратных, аналогичных, деформированных, трансформированных и т.д. задач. Весь теоретический материал делится на логически завершенные единицы и изучается не по отдельным параграфам, а целиком: сначала – понятие, затем закономерности между ними и их практическое применение. При этом основной материал повторяется на каждом уроке, что способствует его лучшему запоминанию. В конце каждого блока проводится обобщающий урок. Основная цель таких уроков – это установление связей между отдельными понятиями, явлениями, законами, теориями. Причем обобщение фундаментальных знаний можно осуществлять на разных уровнях, разными способами. Здесь очень эффективными бывают опорные конспекты [2].
Основные элементы технологии УДЕ :
Совместное и одновременное изучение родственных разделов, одновременное изучение аналогичных или противоположных понятий;
Взаимнообратные задания (прямые и обратные задания);
Матричные задания (использование матриц при объяснении или закреплении материала);
Представление информации в образно-наглядной форме (рисуночная, графическая, табличная);
Блочная подача материала;
Работа на уроке по единому тексту;
Интегрированные знания (интегрированные уроки);
Восстановление деформированных упражнений (метод пустых клеток).[3]
Темы «Корни. Степени. Логарифмы» изучаются в 10 классе в течение второй и третьей четвертях. Имеется необходимость объяснения данных тем одновременно, так как имеется наличие связей – взаимно обратными мыслительными операциями, комплексами взаимно обратных, аналогичных, деформированных задач.
В классном коллективе имеется ребенок с ОВЗ, по умственным возможностям не уступает сверстникам, учиться на «отлично» и «хорошо». Из-за длительного лечения ребенок пропускает занятия. Но изучая темы крупными блоками и дидактический материал, подготовленный с помощью технологии УДЕ, пробелы знаний при решении промежуточных контрольных не выявлены. Подав материал крупными блоками, далее идет этап закрепления новой темы. На закрепление новой темы остается достаточное время, при этом я включаю задания КИМ ЕГЭ с различных сайтов. (https://mathb-ege.sdamgia.ru/ , https://math100.ru/statgrad-baza/ , https://4ege.ru/ и другие)
В своей практике использую следующий дидактический материал:
Карточка №1.
| Восстановить пропущенные числа на тему «Корни и Степени» |
| 
| 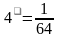
| 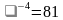
| 
|
| 
| 
| 
| 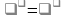
|
| 
| 
| 
|  = = 
|
|  = =
|  =16 =16
| 
| 
|
| 
| 
| 
| 
|
Карточка №2.
| Восстановить пропущенные числа на тему «Логарифмы» |
| 
| 
| 
| 
|
| | 
| 
| 
|
| 
|  = -2 = -2
| | 
|
| 
| 
| 
| 
|
| 
| 
| | 
|
| 
| 
| 
| 
|
| | 
| 
| 
|
| | 
| 
| 
|
Карточка №3. «Интегрированная»
| Восстановить пропущенные числа на тему «Корень. Степень. Логарифмы» |
| а = 4 | 
| 
| |
| а =  | 
| 
| |
| а = 0,09 | 
| 
| 
|
| а = 25 | 
| 
| 
|
| а = 0,01 | 
| 
| |
| а = 5 | 
| 
| 
|
| а = 10 | 
| 
| 
|
| а =  | 
| 
| 
|
Литература
https://www.1urok.ru/categories/9/articles/15313
https://studfile.net/preview/5113703/page:6/
http://www.kripkro.ru/images/news/UDE/sbornik_YDE.pdf стр 38-41 «Применение технологии УДЕ на уроках физики» Борлыкова Г.Д.
Приложение.
После закрепления данной темы идет этап обобщения и систематизации знаний. Лично мною были составлены карточки для игры в математическое домино на тему: «Корни. Степени. Логарифмы».
«Математическое домино» – это быстрая игра с числами, которая может использоваться как обучающий материал. Она позволяет развить такие навыки как логика, стратегическое мышление, внимательность, ну и, конечно, устный счет!
Как играть
Игроки должны с помощью костей домино выполнить любое математическое действие (+, -, x, ÷). Для этого они должны положить одну из своих костей таким образом, чтобы одно из чисел на ней являлось результатом математического действия с двумя соседними числами. При этом неважно, находятся эти числа на одной кости или на разных костях. Если игрок не может поместить кость на поле, он должен взять одну из резерва, положить её перед собой и пропустить ход. Победителем является игрок, который первым разместил все свои кости на игровом поле.
Вместо простых математических действий (+, -, x, ÷) я использовала корни, степени и логарифмы и не кости, а карточки.
Карточки для игры в математическое домино следующего вида:
| Обычное математическое домино | Разработанное мною математическое домино |
| |
|
| Момент игры в математическое домино |
| | См под таблицей |








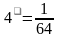
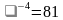




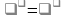



 =
= 
 =
=
 =16
=16


















