Карточка 1 Основное свойство дроби
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
Карточка 3 Сложение и вычитание дробей с разными знаменателями
Просмотр содержимого документа
«Дидактический материал для учащихся с ОВЗ по математике 8 класс»
8класс
Карточка 1 Основное свойство дроби
| Правило | Образцы | Задания ( Вариант 1) |
| Сократить дробь: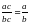 , , где 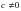
| Сократить дробь: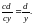 Сократить дробь: 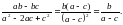
Привести дробь 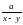 к знаменателю х2 – у2. к знаменателю х2 – у2. 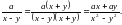
| Сократить дроби: 1) 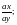 2) 2)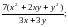 3) 3)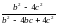 Указание: в заданиях 2) и 3) используй формулы сокращённого умножения: (а-b)(a+b) = a2 – b2 , a2 – 2ab + b2 = (a – b)2 или a2 + 2ab + b2 = (a +b)2. Привести дроби к общему знаменателю: 4) 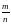 и и 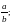 5) 5) 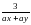 и и 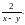 |
| Привести дробь к новому знаменателю: 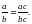
|
Карточка 1 Основное свойство дроби
| Правило | Образцы | Задания ( Вариант 2) |
| Сократить дробь: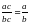 , , где 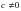
| 1)Сократить дробь: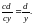 2)Сократить дробь: 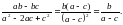
3)Привести дробь 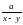 к знаменателю х2 – у2. к знаменателю х2 – у2. 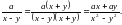
| Сократить дроби: 1) 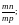 2) 2)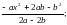 3) 3)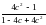 Указание: в заданиях 2) и 3) используй формулы сокращённого умножения: (а-b)(a+b) = a2 – b2 , a2 – 2ab + b2 = (a – b)2 или a2 + 2ab + b2 = (a +b)2. Привести дроби к общему знаменателю: 4) 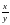 и и 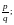 5) 5)  и и  |
| Привести дробь к новому знаменателю: 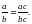
|
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
| Правило | Образцы | Задания ( Вариант 1) |
|  , , где b ≠ 0
 , ,
где b ≠ 0
| 1)  2) 
Указание: 2) в последнем шаге надо разложить знаменатель на множители по формуле c2 – d2 = (c – d)(c + d) и сократить дробь на c – d. | Найти суммы и разности: 1)  2) 2) 3) 3) 4) 4)  5) 5)  ; ; Указание: в заданиях 3), 4) и 5) используй в последнем шаге формулы сокращённого умножения: (а-b)(a+b) = a2 – b2 , a2 – 2ab + b2 = (a – b)2 или a2 + 2ab + b2 = (a +b)2.
|
Карточка 2 Сложение и вычитание дробей с одинаковыми знаменателями
| Правило | Образцы | Задания ( Вариант 2) |
|  , , где b ≠ 0
 , ,
где b ≠ 0
| 1)  2) 
Указание: 2) в последнем шаге надо разложить знаменатель на множители по формуле c2 – d2 = (c – d)(c + d) и сократить дробь на c – d. |
Найти суммы и разности: 1)  2) 2) 3) 3) 4) 4)  5) 5)  . . Указание: в заданиях 3), 4) и 5) используй в последнем шаге формулы сокращённого умножения: (а-b)(a+b) = a2 – b2 , a2 – 2ab + b2 = (a – b)2 или a2 + 2ab + b2 = (a +b)2.
|
Карточка 3 Сложение и вычитание дробей с разными знаменателями
| Правило | Образцы | Задания ( Вариант 1) |
|  , , где b,d ≠ 0 1) найдите общий зна -менатель, состоящий из произведения всех различных выражений; 2) умножить числитель и знаменатель каждой дроби на их дополнительный множитель; 3)выполнить действия. |  Общий знаменатель: (а – b)2(а + b). Дополнительный множитель для первой дроби – это (a + b) , для второй дроби – это (а – b)
Указание: при составлении общего знаменателя из всех степеней берут степень с наибольшим показателем; в нашем случае это (а – b)2 |
Найти суммы и разности: 1)  2) 2) 3) 3) 4) 4)  5) 5)  . . Указание: в задании 2) знаменатели -противоположные выражения, в задании 5) надо вначале разложить на множители каждый знаменатель, используя ФСУ,а затем составить общий знаменатель. ФСУ: a2 – b2 =(а-b)(a+b) , (a – b)2 = a2 – 2ab + b2, (a +b)2 = a2 + 2ab + b2
|
Карточка 3 Сложение и вычитание дробей с разными знаменателями
| Правило | Образцы | Задания ( Вариант 2) |
|  , , где b,d ≠ 0 1) найдите общий зна -менатель, состоящий из произведения всех различных выражений; 2) умножить числитель и знаменатель каждой дроби на их дополнительный множитель; 3)выполнить действия. |  Общий знаменатель: (а – b)2(а + b). Дополнительный множитель для первой дроби – это (a + b) , для второй дроби – это (а – b)
Указание: при составлении общего знаменателя из всех степеней берут степень с наибольшим показателем; в нашем случае это (а – b)2 |
Найти суммы и разности: 1)  2) 2) 3) 3) 4) 4)  5) 5)  . . Указание: в задании 2) знаменатели -противоположные выражения, в задании 5) надо вначале разложить на множители каждый знаменатель, используя ФСУ,а затем составить общий знаменатель. ФСУ: a2 – b2 =(а-b)(a+b) , (a – b)2 = a2 – 2ab + b2, (a +b)2 = a2 + 2ab + b2
|
Карточка 4 Умножение дробей. Возведение дроби в степень
| Правило | Образцы | Задания ( Вариант 1) |
|  , , где b,d ≠ 0
 , ,
где b ≠ 0 или 
| 1)Выполни умножение:  2) 
3)  Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби Указание: В задании 1)и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
|
Найти произведение дробей: 1)  2) 2)  3)  4) Вычислить:  Указание: В задании 3) и 4) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки, а затем сократите дроби
|
Карточка 4 Умножение дробей. Возведение дроби в степень
| Правило | Образцы | Задания ( Вариант 2) |
|  , , где b,d ≠ 0
 , ,
где b ≠ 0 или 
| 1)Выполни умножение:  2) 
3)  Указание: В задании 1) и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби Указание: В задании 1) и 2) вначале разложите числители и знаменатели на множители, а затем сократите дроби
|
Найти произведение дробей: 1)  2) 2)  3)  4) Вычислить:  Указание: В задании 3) и 4) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки, а затем сократите дроби
|
Карточка 5 Деление дробей
| Правило | Образцы | Задания ( Вариант 1) |
|
 , , где b,с,d ≠ 0
| Выполнить деление: 1)  2) 
Указание: В задании 1) вначале разложите числители и знаменатели на множители, используя вынесение общего множителя за скобки и формулы сокращённого умножения(ФСУ), а затем сократите дробь ФСУ: х2 – у2 = (х – у)(х + у) |
Найти частное дробей: 1)  2) 2) 3)  4) 5)  Указание: В задании 3),4),5) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки и используя ФСУ, а затем сократите дроби
|
Карточка 5 Деление дробей
| Правило | Образцы | Задания ( Вариант 2) |
|
 , , где b,с,d ≠ 0
| Выполнить деление: 1)  2) 
Указание: В задании 1) вначале разложите числители и знаменатели на множители, используя вынесение общего множителя за скобки и формулы сокращённого умножения(ФСУ), а затем сократите дробь ФСУ: х2 – у2 = (х – у)(х + у) |
Найти частное дробей: 1)  2) 2) 3)  4) 5)  Указание: В задании 3),4),5) вначале разложите числители и знаменатели на множители, вынеся общий множитель за скобки и используя ФСУ, а затем сократите дроби
|
Карточка 6 Свойства квадратных корней
| Правила | Образцы | Задания ( Вариант 1) |
|

если  . .  если если  , b 0. , b 0.

 , если , если  . .
| Вычислить: 1) 2) ; ; 3) 4) | Вычислите: 1) ; ; 2) ; ; 3) ; ; 4)  ; ; 5) . .
|
Карточка 6 Свойства квадратных корней
| Правила | Образцы | Задания ( Вариант 2) |
|

если  . .  если если  , b 0. , b 0.

 , если , если  . .
| Вычислить: 1) 2) ; ; 3) 4) | Вычислите: 1) ; ; 2) ; ; 3) ; ; 4)  ; ; 5) . .
|
Карточка 7 Вынесение множителя из – под знака корня
| Правила | Образцы | Задания ( Вариант 1) |
|

если  . .

| 1) ; ; 2) ; ; 3) , т.к. у2 ≥ 0; , т.к. у2 ≥ 0; 4)  Пояснения: т.к. по условию z7 ≥ 0, то z ≥ 0. Но тогда  . .
| Вынести множитель из – под корня: 1) ; 2) ; 2) ; ; 3) где х 0, где х 0, у. 4)  ; 5) ; 5) . .
|
Карточка 7 Вынесение множителя из – под знака корня
| Правила | Образцы | Задания ( Вариант 2) |
|

если  . .

| 1) ; ; 2) ; ; 3) , т.к. у2 ≥ 0; , т.к. у2 ≥ 0; 4)  Пояснения: т.к. по условию z7 ≥ 0, то z ≥ 0. Но тогда  . .
| Вынести множитель из – под корня: 1) ; 2) ; 2) ; ; 3) где d 0, с. где d 0, с. 4)  ; 5) ; 5) . .
|
Карточка 8 Внесение множителя под знак корня
| Правила | Образцы | Задания ( Вариант 1) |
|
Чтобы внести множитель под знак корня, нужно: 1)возвести его в квадрат; 2) если этот множитель отрицателен, изменить его знак при внесении под корень, а «минус» оставить перед корнем.
| Заменить выражение  квадратным корнем или выражением, ему противоположным: квадратным корнем или выражением, ему противоположным: а ≥ 0;  а ≤ 0;  Впервом случае получился квадратный корень, а во втором – выражение, противоположное квадратному корню
| Заменить выражение квадратным корнем или выражением, ему противоположным: 1) ; 2) ; 2) ; ; 3) где х 0; где х 0; 4)  ; 5) ; 5) . . |
Карточка 8 Внесение множителя под знак корня
| Правила | Образцы | Задания ( Вариант 2) |
|
Чтобы внести множитель под знак корня, нужно: 1)возвести его в квадрат; 2) если этот множитель отрицателен, изменить его знак при внесении под корень, а «минус» оставить перед корнем.
| Заменить выражение  квадратным корнем или выражением, ему противоположным: квадратным корнем или выражением, ему противоположным: а ≥ 0;  а ≤ 0;  Впервом случае получился квадратный корень, а во втором – выражение, противоположное квадратному корню
| Заменить выражение квадратным корнем или выражением, ему противоположным: 1) ; 2) ; 2) ; ; 3) где у где у 4)  ; 5) ; 5) . . |
Карточка 9 Решение неполных квадратных уравнений
| Правила | Образцы | Задания ( Вариант 1) |
| Уравнение вида ах2 = 0 решается так: ах2 = 0 х2 = 0(а ≠ 0) х = 0. Уравнение вида ах2+ bх = 0 решается так: ах2+ bх = 0 х(ах + b) = 0 x = 0 или ax + b = 0 x = 0 или x =  . . Уравнение вида ах2+ c = 0 решается так: ах2+ c = 0, ax2 = -c,  , где а ≠ 0; , где а ≠ 0;
1)если  , то корней нет; , то корней нет; 2)если  ,то х = 0; ,то х = 0; 3) если  , то х = , то х =  . . | Решить уравнения: 1) 2х2 + 8 = 0 - уравнение вида ах2+с=0; 2х2 = - 8, х2 = -4. Ответ: корней нет
2) 3х2 – 2х = 0 - уравнение вида ах2+ bx =0. 3х2 – 2х = 0, x(3x – 2) = 0, x = 0 или 3x – 2 = 0, x = 0 или  . Ответ: 0; . Ответ: 0;  3)7х2 – 8 = 0 – уравнение вида ах2 + с = 0. 7х2 – 8 = 0, 7х2 = 8, х2 =  , ,  . Ответ: . Ответ: 
4)6х2 = 0 – уравнение вида ах2 = 0. 6х2 = 0, х2 = 0, х = 0. Ответ: 0
|
1) 3х2 + 3 = 0;
2) –х2 + 5х = 0;
3) 7х2 – 28 = 0;
4) –х2 = 0;
5) 4(х – 1)2 – 16 = 0 |
Карточка 9 Решение неполных квадратных уравнений
| Правила | Образцы | Задания ( Вариант 2) |
| Уравнение вида ах2 = 0 решается так: ах2 = 0 х2 = 0(а ≠ 0) х = 0. Уравнение вида ах2+ bх = 0 решается так: ах2+ bх = 0 х(ах + b) = 0 x = 0 или ax + b = 0 x = 0 или x =  . . Уравнение вида ах2+ c = 0 решается так: ах2+ c = 0, ax2 = -c,  , где а ≠ 0; , где а ≠ 0;
1)если  , то корней нет; , то корней нет; 2)если  ,то х = 0; ,то х = 0; 3) если  , то х = , то х =  . . | Решить уравнения: 1) 2х2 + 8 = 0 - уравнение вида ах2+с=0; 2х2 = - 8, х2 = -4. Ответ: корней нет
2) 3х2 – 2х = 0 - уравнение вида ах2+ bx =0. 3х2 – 2х = 0, x(3x – 2) = 0, x = 0 или 3x – 2 = 0, x = 0 или  . Ответ: 0; . Ответ: 0;  3)7х2 – 8 = 0 – уравнение вида ах2 + с = 0. 7х2 – 8 = 0, 7х2 = 8, х2 =  , ,  . Ответ: . Ответ: 
4)6х2 = 0 – уравнение вида ах2 = 0. 6х2 = 0, х2 = 0, х = 0. Ответ: 0
|
1) 5х2 – 5 = 0;
2) 3х2 + 6х = 0;
3) 5х2 + 20 = 0;
4) 4х2 = 0;
5) 5(х – 2)2 – 45 = 0 |
Карточка 10 Решение квадратных уравнений по формуле
| Правила | Образцы | Задания ( Вариант 1) |
| Чтобы решить квадратное уравнение ах2 + bx + c = 0 по формуле нужно: вычислить его дискриминант D = b2 – 4ac. 1) Если DD = 0, вычислить единственный корень по формуле  ; 3) если D 0 , вычислить два корня по формуле ; 3) если D 0 , вычислить два корня по формуле  . . | Решить уравнения: 1) 8х2 +4х + 3 = 0 ; a = 8, b = 4, c = 3 Находим дискриминант D = b2 – 4ac, D = 42 – 4·8·3 = 16 – 96 = - 80 нет корней. Ответ: нет корней. 2) х2 – 6х + 9 = 0 ; a = 1, b = - 6, c = 9 D = b2 – 4ac = (-6)2 - 4·1·9 =36 – 36 = 0 Находим единственный корень по формуле  = =  . . Ответ: 3. 3) 5х2 – 3х – 2 = 0 ; a = 5, b = - 3, c = - 2. D = b2 – 4ac = (-3)2 - 4·5·(- 2) =9 + 40 =49,  = = 

Ответ: -0,4; 1
|
1) 3х2 + 5х – 8 = 0;
2) х2 + 5х + 10 = 0;
3) 7х2 – 14х + 7 = 0;
4) – х2+ 3х + 4 = 0;
5) 4(х - 1)2 – 16х = 0 |
Карточка 10 Решение квадратных уравнений по формуле
| Правила | Образцы | Задания ( Вариант 2) |
| Чтобы решить квадратное уравнение ах2 + bx + c = 0 по формуле нужно: вычислить его дискриминант D = b2 – 4ac. 1) Если DD = 0, вычислить единственный корень по формуле  ; 3) если D 0 , вычислить два корня по формуле ; 3) если D 0 , вычислить два корня по формуле  . . | Решить уравнения: 1) 8х2 +4х + 3 = 0 ; a = 8, b = 4, c = 3 Находим дискриминант D = b2 – 4ac, D = 42 – 4·8·3 = 16 – 96 = - 80 нет корней. Ответ: нет корней. 2) х2 – 6х + 9 = 0 ; a = 1, b = - 6, c = 9 D = b2 – 4ac = (-6)2 - 4·1·9 =36 – 36 = 0 Находим единственный корень по формуле  = =  . . Ответ: 3. 3) 5х2 – 3х – 2 = 0 ; a = 5, b = - 3, c = - 2. D = b2 – 4ac = (-3)2 - 4·5·(- 2) =9 + 40 =49,  = = 

Ответ: -0,4; 1
|
1) 5х2 + х – 6 = 0;
2) 3х2 + 6х + 3 = 0;
3) 4х2 – 11х – 7 = 0;
4) х2+ 4х + 5 = 0;
5) 5(х - 2)2 – 45х = 0 |
Карточка 11 Решение числовых неравенств
| Правила | Образцы | Задания ( Вариант 1) |
| При решении числовых неравенств можно: 1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные; 2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства; 3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства | Решить неравенство: -2(х – 3) 3(x + 5). Решение: Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 3x + 15. Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х – 3х 15 – 6. Приведём подобные слагаемые: -5х 9, разделим обе части неравенства на отрицательное число – 5, меняя знак неравенства: х Ответ: 
| 1) х + 1
2) 3 – x ;
3) 2x – 7 x;
4) 6 – x ;
5) 2(x – 4) 5 – 7x |
Карточка 11 Решение числовых неравенств
| Правила | Образцы | Задания ( Вариант 2) |
| При решении числовых неравенств можно: 1) переносить слагаемые из одной части неравенства в другую, изменив знаки этих слагаемых на противоположные; 2) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства; 3) ) делить обе части неравенства на одно и то же положительное число, сохраняя знак неравенства | Решить неравенство: -2(х – 3) 3(x + 5). Решение: Раскроем скобки, умножив числа перед скобками на каждое слагаемое в скобках: -2х + 6 3x + 15. Перенесём слагаемые с неизвестным влево, а без неизвестных вправо, изменяя их знаки: -2х – 3х 15 – 6. Приведём подобные слагаемые: -5х 9, разделим обе части неравенства на отрицательное число – 5, меняя знак неравенства: х Ответ: 
| 1) х + 2 6;
2) 2 – x ;
3) 3x – 2 2x;
4) 2 – x ;
5) -(x + 3) 4 – 6x |






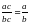 ,
,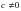
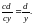
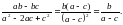
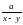 к знаменателю х2 – у2.
к знаменателю х2 – у2.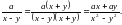
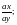 2)
2)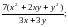 3)
3)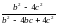
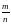 и
и 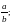 5)
5) 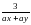 и
и 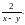
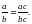
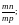 2)
2)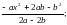 3)
3)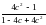
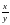 и
и 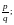 5)
5) 









