Докаева Анастасия Сергеевна

1.ОПРЕДЕЛЕНИЕ РАЗЛИЧИЙ В РАЗВИТИИ УМСТВЕННЫХ ДЕЙСТВИЙ У ДЕТЕЙ 6-ТИ ЛЕТ.

П од умственными действиями обычно понимаются такие, которые выполняются во внутреннем, мысленном плане, без опоры на внешние средства. Названные действия связаны с оперированием образами и представлениями предметов, явлений и событий.

Один из основных видов умственной деятельности – комбинирование , направленное в ходе решения задач на поиск разных вариантов получения требуемого результата, на разработку разных способов достижения поставленной цели.

В развитии комбинаторных действий выделяются два уровня. Первый из них отличается малой продуктивностью комбинирования, поскольку дети предлагают варианты решения задачи, либо получающиеся путем незначительного изменения начального способа задачи, либо возникающие случайным путем. Такое положение определяется затруднениями в оперировании наглядными представлениями, когда ребенку сложно изменить найденный состав способа решения, - в частности , переставив его звенья местами.

Второй уровень развития комбинаторных умственных действий характеризуется высокой продуктивностью в разработке разных способов решения, поскольку в этом случае дети осуществляют систематический поиск вариантов решения. Это объясняется наличием у таких детей возможностей легко оперировать представлениями, не испытывая трудностей в изменении сочетания звеньев в найденном способе решения задачи. Для определения различий в развитии комбинаторных умственных действий целесообразно использовать такие задачи, в которых возможны (по особенностям их построения) разные варианты успешного решения.

При этом необходимо и то, чтобы способ решения складывался из отдельных звеньев (как сумма слагаемых). Тогда создаются хорошие возможности для разработки разных сочетаний таких звеньев как разных способов достижения цели. Вместе с тем такой подход позволит достаточно детально охарактеризовать особенности комбинирования при решении задач. Разработанная нами методика “переходы” включает задачи, отвечающие указанным требованиям. Конкретный смысл таких задач заключается в том, чтобы найти разные пути от одной точки некоторого лабиринта к другой. В задачах используются простые геометрические фигуры (треугольник, круг, квадрат и др.) с тем, чтобы дети, 6 лет, как обычно, не умеющие читать, писать и считать, могли сами зафиксировать свое решение, нарисовав ту или иную фигуру.

Проведение диагностического занятия

Групповое занятие с целью определения различий в уровне развития комбинаторных умственных действий строится следующим образом.

1. Учитель, проводящий диагностическое занятие, приходит в класс (группу) с комплектом бланков (см. приложение к разделу 1), на которых имеются условия задач.

2. На классной доске изображается большой, размером приблизительно 60 на 60 см, лабиринт квадратной формы, который включает девять изображений разных геометрических фигур, помещенных в кругах (рис.1).

3. Детям говорится: “Сегодня будем решать интересные задачи. Посмотрите на доску. Там нарисованы круги. В каждом круге есть какая-то одна фигурка. В кругах наверху есть треугольник, круг и ромб. В кругах внизу есть крючок, квадрат и стрелка. В кругах посередине есть точка, крестик и полукруг. Между всеми кругами есть линии – дорожки, по которым можно пройти от одного круга к другому, от одной фигурки к другой.

4. Теперь решим задачу: по каким двум дорожкам можно пройти от круга, где треугольник, к кругу, где крестик?… Кто догадался? … Верно, от треугольника можно сначала пойти к точке, а потом к крестику.

А еще как можно пройти по двум дорожкам от треугольника к крестику? Кто скажет?… Правильно, еще можно так пройти: от треугольника к кругу, а от круга к крестику.

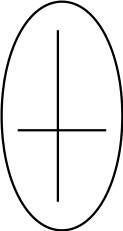
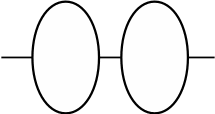
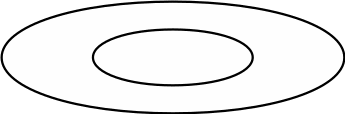
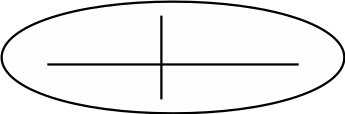
5. Теперь посмотрим, как можно записывать решение задач. Например, нужно узнать, как можно по-разному пройти от круга к треугольнику по двум дорожкам?… Условия этой задачи нарисуем так (рис.2). Кто придумал это решение?…Верно, сначала можно пройти от круга к точке, а потом к треугольнику. Нарисуем это решение (рис.3):

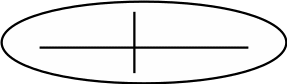
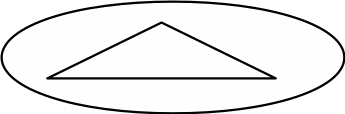
Как еще можно пройти?… Правильно, еще можно от круга пойти сначала к крестику, а потом от него к треугольнику. Нарисуем это решение (рис.4).

Вот так записывается решение задач, где нужно найти разные пути от одной фигурки к другой: нужно просто нарисовать в свободных кругах фигурки, которые стоят на дорожках по пути.

“Сейчас я раздам вам листы, где есть похожие задачи”,- учитель раздает бланки (см.приложение к разделу 1, где даны 4 равноценных варианта диагностического задания).

6.“Посмотрите на лист. На самом врху есть задача для тренировки, - в ней нужно найти разные пути из двух дорожек. Дальше, после черты идет первая основная задача: в ней нужно найти разные пути из трех дорожек. Дальше, после двойной черты, в самом низу листа есть вторая основная задача, - в ней тоже нужно найти разные пути из трех дорожек.

7. Теперь решим тренировочную задачу, которая на самом верху листа. В ней нужно найти разные пути из двух дорожек от круга к крестику. Записывайте решение, - разные пути,- так же, как мы делали это на доске: в свободный круг рисуйте фигурку, которая встречается на пути. Решайте, глядя на доску, где нарисованы дорожки и фигурки”.

8. Дети решают тренировочную задачу, а учитель проходит по классу и контролирует правильность записи решения ( но не правильность решения), отвечая на вопросы и поправляя ошибки в оформлении решения.

9. “Давайте теперь проверим решение этой задачи”,- учитель рисует на доске задание из бланка тренировочной задачи (рис.5).

1























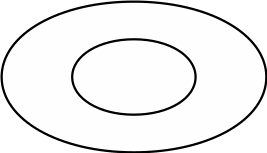
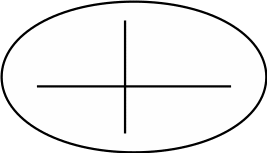
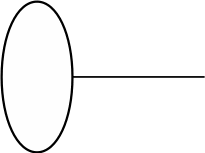
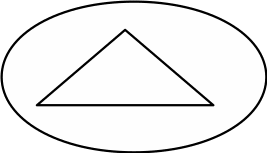
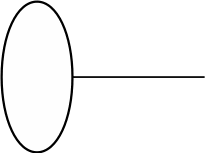
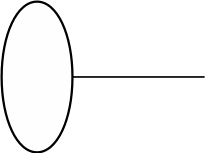
0. “Кто скажет, как можно пройти от круга к крестику по двум дорожкам, через какую фигурку по пути?… Верно, можно пройти через треугольник. Запишем это решение”,- учитель вписывает треугольник в самое верхнее условие задачи.

“Как еще можно пройти по двум дорожкам от круга к крестику?… Правильно, еще можно пройти через точку”,- учитель вписывает точку во второе сверху условие задачи (рис.6).

“Еще какой может быть путь из двух дорожек от круга к крестику?… Через треугольник?… Нет, такое решение уже было. Нужно придумать новое… Верно, еще можно пройти через ромб”,- учитель вписывает ромб в следующее условие задачи (рис.6).

“Есть еще какой-нибудь путь от круга к крестику из двух дорожек?… Никто не знает?…Тогда я скажу: можно еще пройти через полукруг”,- учитель вписывает полукруг в последнее условие задачи (рис.6).

11. “Вот так решаются задачи, где нужно найти разные пути из двух дорожек и нарисовать в свободном круге одну фигурку”.

12. “Теперь сами, без проверки решайте следующую задачу на листе, - она находится дальше, под чертой. В ней нужно найти разные пути из трех дорожек и нарисовать фигурки, которые встретятся по пути”.

13. На решение первой основной задачи отводится 10 минут, - независимо от того, кто сколько успел найти решений. Затем учитель предлагает приступить к решению второй основной задачи . Детям при этом напоминается, что и во второй задаче нужно найти разные пути из трех дорожек и нарисовать две фигурки в кругах. На решение второй основной задачи также отводится 10 минут. После этого работа заканчивается и учитель собирает бланки с решениями задач.

В целом, таким образом, все диагностическое занятие, включая инструктирование и решение тренировочной задачи, может занять 30-35 минут.

Обработка результатов.

Результаты решения задач, находящиеся на бланках, можно обрабатывать, сверяясь с КЛЮЧОМ , в котором представлены все возможные варианты решения двух основных задач. При этом, каждому варианту бланка соответствует свой КЛЮЧ.

Истолкование результатов.

В каждом из 4 вариантов диагностического задания представлены две задачи, имеющие значительное количество разных способов решения: первая задача – 12, вторая – 9 способов.

Как уже отмечалось выше, умственные действия с низкой продуктивностью комбинирования характеризуются, как правило случайным несистематическим варьированием способа решения задачи, а умственные действия с высокой продуктивностью комбинирования характеризуются систематическим, планомерным варьированием. При несистематическом варьировании дети решают первую задачу обычно так (рис 7).

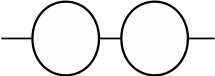
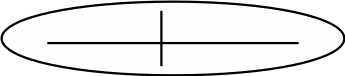
Как можно заметить, предложенные 4 варианта решения не имеют между собой никакой связи и возникают, как показали наблюдения за детьми, случайно, неожиданно.

Иначе решают задачу дети, владеющие систематическим комбинированием. (рис 8).

Рассмотрение приведенных шести вариантов решения задачи свидетельствует о наличии определенного плана варьирования: последовательно, как можно было заметить, наблюдая за действиями детей, разрабатываются пары вариантов с общим звеном в способе решения. Вместе с тем практика использования методики “переходы” показала, что и в рамках несистематического комбинирования, и в рамках систематического комбинирования дети показывают разную продуктивность в поисках вариантов решения задачи. Это позволяет в каждом виде комбинирования выделить два уровня продуктивности: разработка ребенком 1-2 вариантов способа решения задачи свидетельствует о наличии у него1 уровня несистематического комбинирования, 3-4 вариантов – 2 уровня несистематического комбинирования, 5-6 вариантов – 1 уровня систематического комбинирования, 7-8 - 2 уровня систематического комбинирования.

В целом, таким образом, методика “переходы” позволяет выделить среди детей 6 лет разные уровни развития умственных действий, связанных с несистематическим и систематическим комбинированием способа решения задач.

Бланк 1 приложение 1

Бланк 2

Бланк 3

Бланк 4

К люч к бланку 1

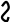
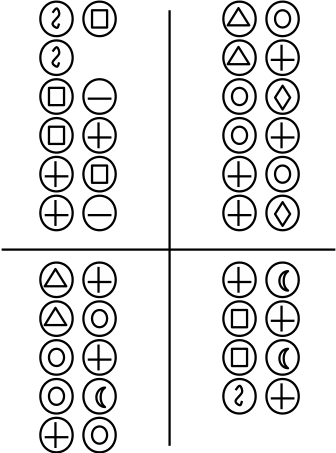
К















































































































люч к бланку 2

К











































































































люч к бланку 3

Rлюч к бланку 4