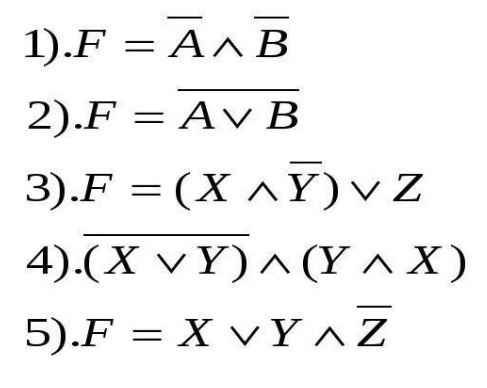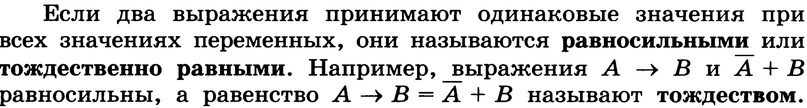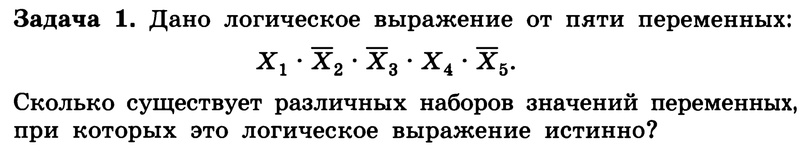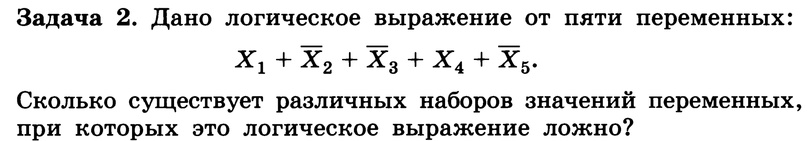Просмотр содержимого документа
«Доказательство логических тождеств с помощью таблиц истинности»
Доказательство логических тождеств с помощью таблиц истинности
Повторение
Задача 1. Среди приведенных ниже предложений указать те, которые являются высказываниями, и те, которые не являются:
Екатеринбург – столица Урала;
студент Уральского федерального университета;
Луна – спутник Земли;
x 0 ;
число 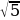 – иррациональное.
– иррациональное.
Задача 2. Среди следующих высказываний указать элементарные и составные, в составных высказываниях выделить грамматические связки:
число 9 не делится на 3;
число 21 делится на 3 и на 7;
число 3 является делителем числа 27;
если число 15 делится на 5, то оно делится на 3;
число 18 делится на 9 тогда и только тогда, когда 9 делится на 3.
Задача 3. Прочитайте составные выражения:
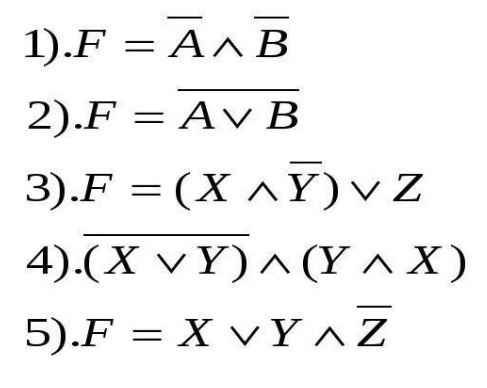
Изучение нового материала
Логическое тождество — это утверждение, которое является верным независимо от значений переменных или истинности других утверждений.
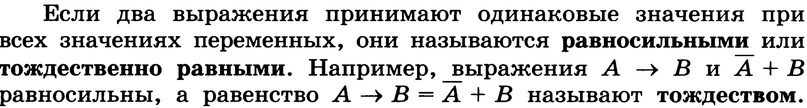
Законы алгебры логики представляют из себя логические тождества

С помощью таблиц истинности можно не только выяснить все возможные значения для различных комбинаций значений входящих в логическое выражение переменных, но и доказывать логические тождества.
Алгоритм построения таблицы истинности
заполнить шапку таблицы, включив в неё переменные и операции
выписать наборы входных переменных
провести заполнение таблицы по столбцам.
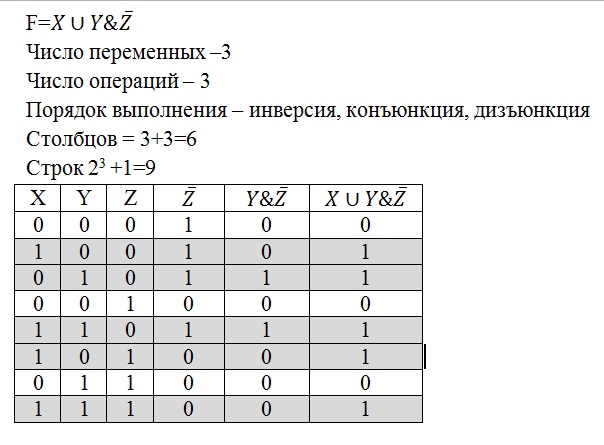
Доказательство логических тождеств с помощью таблиц истинности
Для доказательства тождества построим таблицу истинности
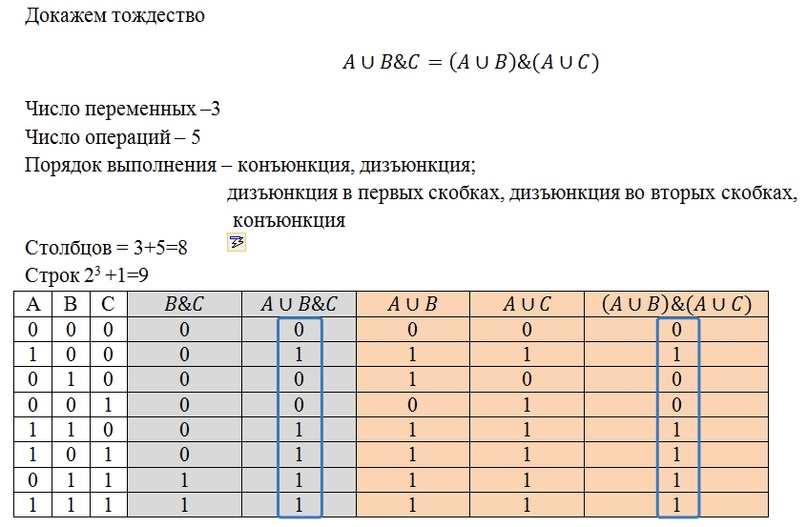
Значения левой и правой частей тождества совпадают для всех возможных сочетаний значений, входящих в тождество логических переменных. Значит, тождество доказано.
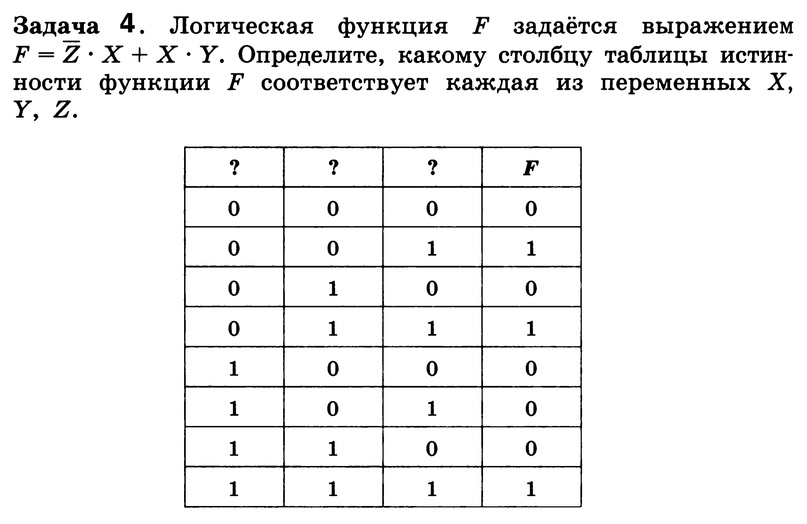
Задачи для решения на уроке
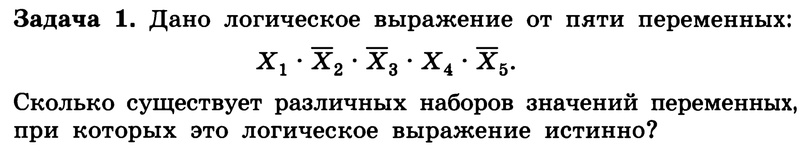
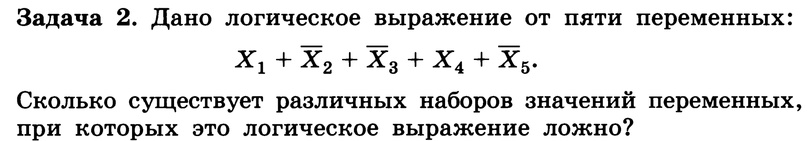
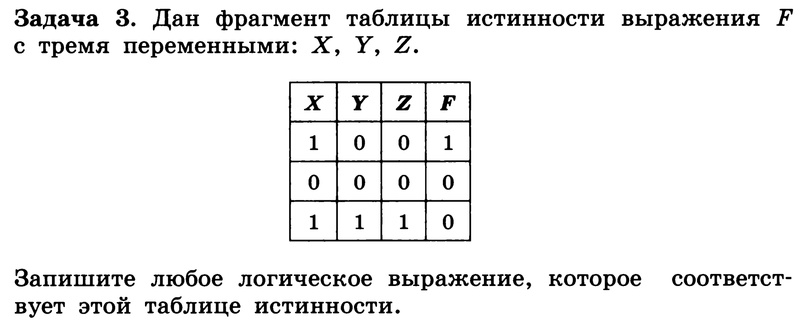
Домашнее задание
Изучить § 17 (Логические выражения). С помощью таблицы истинности докажите распределительный закон и законы де Моргана.







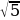 – иррациональное.
– иррациональное.