|
| Соловченкова Е.А. учитель математики и информатики МКОУ «СОШ с.Найфельд» |
Проблемы мотивационного характера в
школьном математическом образовании.
Каждый учитель желает, чтобы его учащиеся хорошо учились, с желанием занимались на уроках и проявляли интерес к его предмету. Развитие и формирование мотивации учебной деятельности школьника является одной из основных задач современной школы.
Учение только тогда станет для детей радостным и привлекательным, когда они сами будут учиться: проектировать, конструировать, исследовать, открывать, т.е. познавать мир в подлинном смысле этого слова. А это возможно только в процессе самостоятельной учебно-познавательной деятельности на основе современных педагогических технологий.
И какими бы знаниями мы ни обладали, какими методиками не владели, без положительной мотивации, без создания ситуации успеха на уроке, такой урок обречен на провал, он пройдет мимо сознания учащихся, не оставив следа в нем.
Хорошо известно, что ничто так не привлекает внимания и не стимулирует работу ума, как удивительное. поэтому мною используются такие приемы, которые стимулируют внутренние ресурсы – процессы, лежащие в основе интереса.
В своей работе я использую следующие методические приемы, которые влияют на формирование мотивации, я думаю, что каждый учитель использует эти методы, поэтому некоторые вспомнят, некоторые – узнают что-то новое:
Практически все задачи по математике имеют применение в жизни. Это могут быть:
- геометрическая прогрессия в экономике;
- задачи на проценты и сложные проценты;
- приложение определенного интеграла в экономике;
- золотое соотношение, симметрия;
- подобие треугольников;
- физический материал на уроках математики;
- задачи с профнаправленностью (использование математических знаний в кулинарии, торговле, в раскрое одежды и в строительстве).
Исторический материал на уроках – один из стимулов учебного процесса
История возникновения единиц измерения длины, площади, массы, времени может стать хорошим дополнением уроков в 5 классе при изучении темы «Измерение величин», оживить их, сделать интересными и познавательными.
При проведении таких уроков можно использовать красочные слайды, которые могут сделать сами ученики.
- умножение одночлена на многочлен – «фонтанчик»
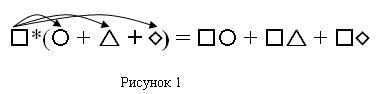
- буква o меняется на и:
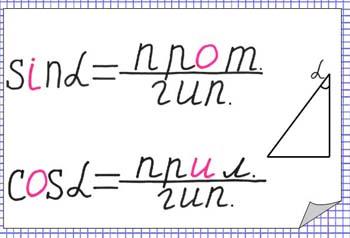
- рука – помощник в запоминании тригонометрии:
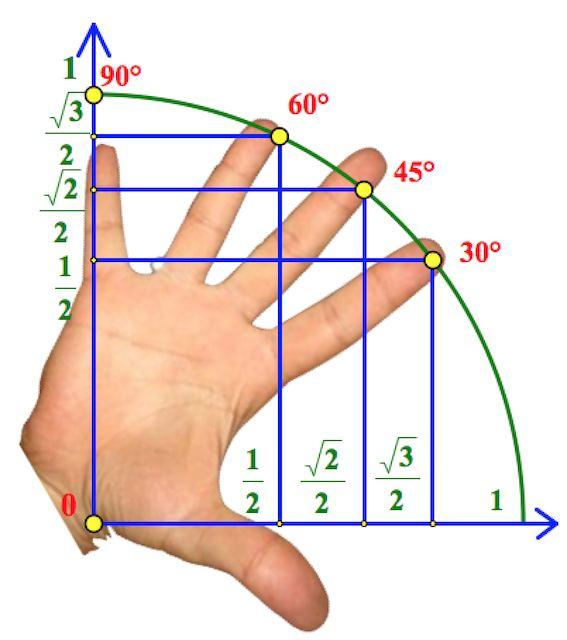
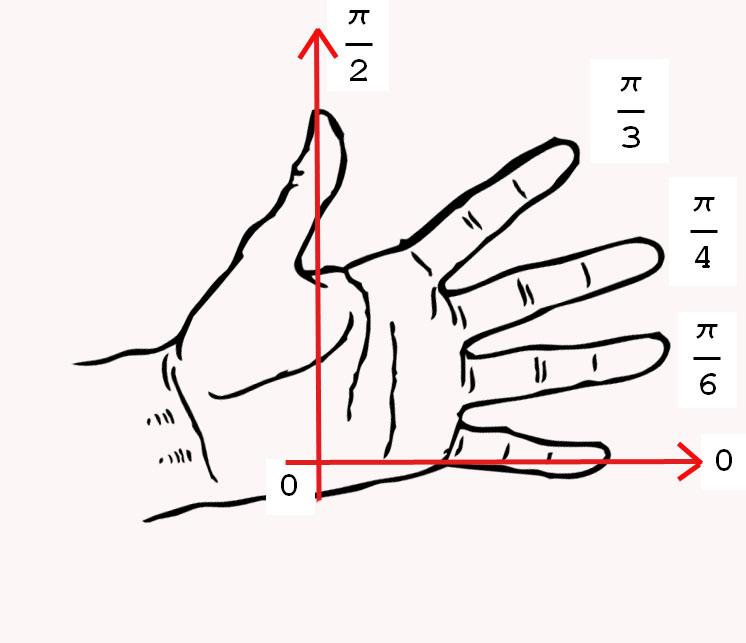
- при объяснении темы «Правильные и неправильные дроби» можно использовать ассоциацию с снеговиками.
Посмотрите внимательно перед вами снеговики:

Скажите, какой на ваш взгляд снеговик будет неправильной и правильной формы? Почему? (Учащимся предлагается сформулировать понятия правильной и неправильной дроби).
- на физминутках можно закреплять с помощью движений рук названия углов (прямой, острый, развернутый, тупой), параллельность, пересечение и перпендикулярность прямых.
Известно, что усвоение школьниками знаний, умений и навыков проходит неравномерно, некоторые ребята с трудом запоминают правила, теоремы, алгоритмы решения заданий.
Для преодоления этих трудностей на своих уроках использую мнемонические правила, которые предлагаю ребятам в стихах, таблицах, рисунках, высказываниях, записях и других видах работ.
Число Пи
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Ну и дальше надо знать,
Если мы вас спросим -
Это будет пять, три, пять,
Восемь, девять, восемь.
Десятичные дроби вычти, сложи,
Цифру под цифрой строго пиши,
И запятые все сохраняй,
В ряд их пиши, не забывай!
При раскрытии скобок даю ребятам правило в такой форме:
Перед скобкой “плюс” стоит
Он о том и говорит,
Что ты скобки опускай,
Да все числа выпускай.
Перед скобкой “минус” строгий
Загородит нам дорогу.
Чтобы скобки убирать,
Надо знаки поменять.
- ( -2а +3в) +( -4а +в) =2а – 3в – 4а + в = - 2а – 2в.
Ребятам нравится, когда уроки проходят в кабинете информатики


-
Работа с тестами, разработанными в Excel , в MyTest, онлайн тесты 

В 6 классе на уроке «Изменение величин» мы с ребятами строили график изменения температуры воздуха (температуру ученики предварительно измеряли неделю)
Привлечение занимательных приемов, парадоксов, интеллектуальные разминки, логические задания, ребусы, математические квадраты, кроссворды.
Это один из самых популярных приемов, который мне очень нравится и часто мною используется.
Например, при изучении темы «Сложение и вычитание рациональных чисел» школьники хорошо усваивают алгоритм действий, если использовать такой прием: «числа с одинаковыми знаками любят друг друга, поэтому их надо сложить и поставить общий знак, а числа с разными знаками ссорятся – «Кто сильнее, чья возьмет?». А при решении линейных уравнений используется прием «разведчика»: при переходе границы («=») необходимо сменить форму (знак) на чужую.
| 4 | 0 | -9 | 2 | | -3 | 5 | -8 | -4 | | 3 | -7 | 12 | -6 | | -11 | -1 | -5 | 11 |
| Сумма четырех чисел, стоящих в одном из рядов (по вертикали, горизонтали, либо диагонали), равны 1) -10; 2) -24. Назовите эти ряды. Ответ: 1) вторая строка и третий столбец; 2) диагональ -11+(-7)+(-8)+2=-24 |
5x – 2=3 3x - 4=2 9x+8=35 6x-3=21
1 8 27 ?
МЕТРО МЕТР x-8=-3
ОКРУГ КРУГ 4x-7=-3
РОМБ РОМ 6x+4=
Зачада гукр Варунение извененаяст
Пример: 2 х 2 = 5. Доказательство: Имеем числовое тождество 4:4=5:5 Вынесем за скобки общий множитель 4(1:1)=5(1:1). Числа в скобках равны, их можно сократить, получим: 4=5 (!?). Парадокс…
7 кл. Тема «Формулы сокращённого умножения»
Вычисляем (2 х 5)²= 2² х5² = 100
(3 х 4)²= 3² х 4² = 9 х 16 = 144
(5 : 6)² = 5² : 6² = 25 : 36
(3 + 4)² = 3² + 4² = 9 + 16 = 25 Попробуйте сосчитать по-другому.
( 3 + 4)² =7² = 49
Проблемная ситуация создана. Почему разные результаты? ( 3 +4)² ≠ 3² + 4²
Четыре года назад, в 2012 году мы с учениками 6 класса завели тетради для творческих заданий, куда собирали известные задания и придуманные учениками. Урок у нас всегда начинался с решения 2-3 таких заданий, но к сожалению, в такой форме мы проработали только год, но за этот год я поняла, что все дети мыслят интересно, к уроку готовились даже ученики, которым математика давалась с трудом.
Использование художественной литературы: загадки, пословицы, стихи о математических терминах или о великих математиках, математические сказки
Я думаю каждый из учителей использует этот метод на любом этапе урока.
Мне очень нравится высказывание Л.Н.Толстого «Человек есть дробь. Числитель - это сравнительно с другими – достоинства человека; знаменатель – это оценка человеком самого себя. Увеличить свой числитель – свои достоинства – не во власти человека, но всякий может уменьшить свой знаменатель – свое мнение о самом себе, и этим уменьшением приблизиться к совершенству».
В 5-6 классах учителя активно используют пословицы, загадки, кроссворды, менее в старших классах.
В 10 классе при изучении темы «Функции» свойства функций можно рассматривать на пословицах (я также организовывала творческое задание: изобразить пословицу в виде графика).
Например:
«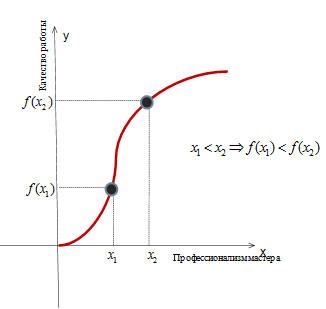 Каков мастер, такова и работа», – гласит пословица. Изобразим графиком, как уровень выполнения работы улучшается по мере улучшения профессионализма мастера.
Каков мастер, такова и работа», – гласит пословица. Изобразим графиком, как уровень выполнения работы улучшается по мере улучшения профессионализма мастера.
Горизонтальная ось графика (ось абсцисс) – это профессионализм мастера (его разряд, талант). По вертикали (ось ординат) будем откладывать качество выполнения работы. Согласно пословице эта функция неизменно возрастает. Какие две точки на оси абсцисс ни взять, для более дальней (чем больше профессионализм мастера) значение функции будет больше (качество работы будет лучше).
Математические сказки можно брать готовые (например, всем знакомую сказку про умножение отрицательных чисел можно предложить ребятам обыграть), а можно чтобы ребята придумали сами.
Очень люблю геометрию, за ее красоту и практическое применение в жизни.
На уроке геометрии в 8 классе, когда изучали подобные треугольники, мы вспоминали известный роман Жюля Верна «Таинственный остров», который содержит не только интересный, захватывающий сюжет, но и достаточно много математических рассуждений. В этом романе картинно описан один из способов измерения высоких предметов.
Ещё один из героев Жюля Верна подсчитывал, какая часть его тела прошла более длинный путь за время кругосветных странствований – голова или ступни ног. Это очень поучительная геометрическая задача, если поставить вопрос определённым образом.
Задача.
Вообразите, что вы обошли земной шар по экватору. Насколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги?
Решение:
Ноги прошли путь 2 R, где R – радиус земного шара. Верхушка же головы прошла при этом 2
R, где R – радиус земного шара. Верхушка же головы прошла при этом 2 (R + 1,7), где 1,7 м – рост человека. Разность путей равна
(R + 1,7), где 1,7 м – рост человека. Разность путей равна

Итак, голова прошла путь на 10,7 м больше, чем ноги.
Любопытно, что в окончательный ответ не входит величина радиуса земного шара. Поэтому результат получится одинаковый и на Земле, и на Юпитере, и на самой маленькой планете.
При изучении темы «Подобие треугольников», «Подобие прямоугольных треугольников» в 9 классе можно рассказать ребятам легенду о Фалесе (когда Фалес измерил высоту пирамиды, когда это не могли сделать даже жрецы Великого Египта).
На уроке геометрии в 9 классе можно познакомить ребят с творчеством поэта Лонгфелло.
П оэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в с
оэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в с воем романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение. Читаем в романе Лонгфелло следующую задачу:
воем романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение. Читаем в романе Лонгфелло следующую задачу:
“Лилия, на одну пядь, поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в двух локтях от прежнего места: исходя из этого требовалось определить глубину озера”. (1 пядь равна 10 дюймам, два локтя 21 дюйму)

Решение:
Решается эта задача на основе теоремы: если две хорды одной окружности пересекаются, то произведение длин частей одной из них равно произведению длин частей другой.
Посмотрим на рисунок, и сразу станет ясно, как находится глубина озера (x):

21 . 21 = 10(x + (x +10)),
441 = 20x + 100,
x = 17,05 (дюймов).
Ответ: 17,05 дюймов.
На самом деле рассказов, где авторы используют математику достаточно много («Путешествия Гулливера» Джонатан Свифт, Д.И.Фонвизин "Недоросль" (на тему свойства 0 и 1 при умножении) и т.д..), также как и ошибок (Джек Лондон «Маленькая хозяйка большого дома», А.С.Пушкин, говоря в «Скупом рыцаре» о далёком горизонте, открывающемся с вершины «гордого холма» и т.д.)
В 5 - 6 классе я зачитываю отрывки из книги моего детства "Алиса в Стране Математики" Лев Генденштейн.
Игра «Кодирование ответов».
Тема «Действия с десятичными дробями»
Учащиеся выполняют действия
0,14 + 0,006 (0,2) М
2 – 0,7 (1,3) О
100 · 0,012 (1,2) Л
0,42 : 7 (0,06) О
3,18 – 1,08 (2,1) Д
5,4 · 0,1 (0,54) Ц
0,4² (0,16) Ы
Находят табличку с полученным ответом, на обратной стороне написана буква. Составляют слово «Молодцы». (Можно писать не букву, а слово, и в результате получится пословица, поговорка или высказывание великих математиков).
деловые игры: «Строители» (8 класс), «Математика и бизнес» (9-11 класс)
интеллектуальные игры: «Поле чудес», «Своя игра», «К доске!», «Математическое состязание»
математические путешествия
Так например в 5 классе мы проводили опыты со стаканом и краской (тема «Окружность»), вырезали круг, опыты с треугольниками, в 6 классе измеряли длину окружность (нить и стаканчик)
Этот метод позволяет объединить всех учеников класса, развивает самостоятельность, творчество, коммуникативность, умение работать с информацией, умение планировать свою деятельность, умение представлять информацию, умение оценивать себя и своих одноклассников.
Суть всех перечисленных приемов состоит в том, чтобы привлечь интерес к предстоящей работе чем-то необычным, загадочным, проблемным, побуждая всех учащихся вовлечься в работу с первых минут урока.
Стимулом для формирования мотивации к учебной деятельности служит также доброжелательный настрой учителя, благоприятный и продуктивный микроклимат на уроке.
Если проанализировать структуру урока, то можно выявить следующее:
В начале урока математики нужно создать условия для осознания учеником того, что полезного и нового он узнает на уроке, где сможет применить усвоенное, какие преимущества ему даст усвоение материала на уроке.
В ходе урока математики создать условия для сохранения и усиления исходной мотивации. Для этого вызвать ориентацию на осознание и понимание способов действий, их оценке, сравнения, получения удовлетворения от самого процесса учения.
В конце урока математики создать условия для оценки достижения задач, поставленных в начале урока, определения причины удачи или неудачи, постановке задач для дальнейшей деятельности. Главная задача конца урока состоит в том, чтобы каждый ученик осознал приобретенный положительный опыт.
Таким образом мотивация учения в рамках урока представляет собой завершенный цикл и проходит ряд этапов: от мотивации начала работы (готовность, включенность) к мотивации хода выполнения работы и затем к мотивации завершения работы (удовлетворенность или неудовлетворенность результатами, постановка дальнейших целей и т. д.)
Благодаря этой работе мотивация, возникнув, превращается в фактор активизации учебного процесса и эффективности обучения и воспитания. Она побуждает человека развивать свои склонности и возможности, оказывает определяющее влияние на формировании личности и раскрытие ее творческого потенциала.
Рассмотрим урок «Жить или курить», который занял призовое место в конкурсе «Методическая копилка» в 2015 году.
В начале урока ребятам была предложена статистическая информация о курении и поставлен проблемный вопрос «Модно ли курить?». Ребята высказывали свое мнение, сформулировали цель урока. Для того, чтобы двигаться дальше необходимо было вспомнить какая пропорциональная зависимость является прямой, какая обратной. И здесь на помощь пришло использование теста в Excel. На протяжении всего урока ребята зарабатывали балы и отмечали в рабочих листах.
В ходе урока ребятам был предложен отрывок из рассказа Тома Сойера «Первая трубка». На следующем этапе урока ребята решали задачи из жизни про вред сигарет (устно, в парах). После ознакомления со статистикой (подготовила ученица), решив задачи ученики сформулировали аргументы против курения, нарисовали в программе Paint рисунок по теме урока.


В конце урока ребята ответили на проблемный вопрос «Жить или курить?», сформулировали аргументы против курения, высказали свое мнение о уроке, о работе каждого.
Как видно, на уроке использовались приемы для формирования мотивации.
Предлагаю интересные идеи для создания проблемных ситуаций и развития мотивации.







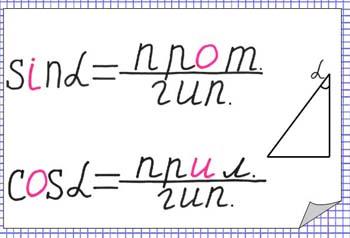







 Каков мастер, такова и работа»
Каков мастер, такова и работа» оэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в с
оэт Г. Лонгфелло был еще и математиком. Наверное, поэтому яркие образы, украшающие математические понятия, которые он использовал в с воем романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение. Читаем в романе Лонгфелло следующую задачу:
воем романе “Кавана”, позволяет запечатлеть некоторые теоремы и их применение. Читаем в романе Лонгфелло следующую задачу:































