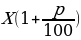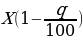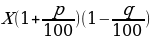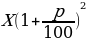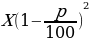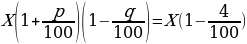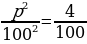Как научиться решать любую банковскую задачу?
В ЕГЭ по профильной математике есть задача под номером 16, к которой школьник почти готов сразу после освоения материала для первых 12-ти заданий.
Как научиться решать экономическую (банковскую) задачу в ЕГЭ по математике
Прототипы для 16-го номера делятся на три большие группы:
Сегодня я расскажу, как научиться структурировать условие любой банковской задачи, как составить по этим данным математическую модель и найти решение.
Главная трудность — школьник плохо понимает условие, ведь с кредитами и вкладами он пока не сталкивался.
Как работает процент по кредиту?
На какую сумму начисляется?
Из каких частей состоит платеж?
Как уменьшается долг?
С чего начать разбор экономической (банковской) задачи в ЕГЭ по математике
Экзамен немного утрирует реальную ситуацию, в жизни кредит работает сложнее. Однако грустно упускать возможность узнать что-то из реальности! Вот кое-какие сведения из опыта кредитования:
Например клиенту придется сверх купить страховку на случай потери работоспособности, ведь банк не хочет терять прибыль даже если на заемщика кирпич упадет. Вы знаете, как работает страховка?
Механизм аннуитетного платежа: часть денег банк забирает себе в качестве дохода, то есть на погашение процентов за пользование кредитом; а на вторую часть уменьшает ваш долг. В реальности это разделение считается по специальной формуле, и совсем не в пользу заемщика.
Например в ипотеке на 10 лет из 20 тысяч ежемесячного платежа на первых порах всего 5 000 рублей идет в счет уменьшения долга, а 15 000 — забирает себе банк! Но каждый раз платеж чуть ребалансируется, и в счет долга идет чуть больше. Так в последних платежах через 10 лет в счет процентов идет буквально пара сотен, а все остальное гасит долг.
Сейчас я поделюсь методическими находками, которые я применяю при изучении данных задач.
Знакомство с экономическими задачами повышенного уровня сложности я начинаю с решения простейших задач на проценты. Вначале мы вспоминаем, что 1% — это одна сотая часть от чего-либо. В задачах, и в жизни часто говорится об изменении какой-либо величины на определенный процент. Разбираем, что это значит?
Понижение цены на 27% означает, что от прежней цены Х убрали 0,27х или прежнюю цену х умножили на 0,73. Наоборот, повышение на 19% означает, что прежняя цена увеличилась на 19%. Если цена была Х, то новая цена составит х + 0,19х = 1,19х. Это является основой для решения простых экономических задач ЕГЭ, причем в условиях задач даны определенные жизненные ситуации из жизни, с которыми ученики уже встречались или им предстоит встретиться в ближайшем будущем.
Рассмотрим примеры задач разного типа из открытого банка заданий ЕГЭ:
1. Пачка сливочного масла стоит 120 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей стоит пачка масла для пенсионера?
Решение.
Скидка на пачку сливочного масла составляет 120 · 0,05 = 6 рублей. Значит, пенсионер за пачку масла заплатит 120 − 6 = 114 рублей.
Ответ: 114.
2. Кроссовки стоили 1600 рублей. После снижения цены они стали стоить 1360 рублей. На сколько процентов была снижена цена на кроссовки?
Решение.
Цена на кроссовки была снижена на 1600 − 1360 = 240 рублей. Разделим 240 на 1600:
240 : 1600 = 0,15. Значит, цена на кроссовки была снижена на 15%.
Ответ: 15.
Легко? Да, легко. Однако не будем спешить. Даже среди подобных задач встречаются интересные и не столь простые задачи, вот пример такой задачи:
В городе N живет 300000 жителей. Среди них 20% детей и подростков. Среди взрослых 35% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
Решение.
Численность детей в городе N составляет 300 000 · 0,2 = 60 000. Численность взрослого населения 300 000 − 60 000 = 240 000 человек. Из них не работает 240 000 · 0,35 = 84 000 человек. Значит, работает 240 000 − 84 000 = 156 000 человек.
Ответ: 156 000.
Для закрепления подобных задач прорешиваем достаточное количество заданий ЕГЭ из открытого банка и только потом переходим к решению сложных задач.
Для решения задач с экономической направленностью повышенного уровня я формулирую несколько важных правил:
1. За 100% мы принимаем ту величину, с которой сравниваем.
2. Если величину х увеличить на р процентов, получим

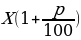
3. Если величину х уменьшить на р процентов, получим

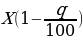
4. Если величину х увеличить на р процентов, а затем уменьшить на q процентов, получим
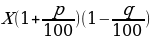
5. Если величину 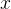 дважды увеличить на
дважды увеличить на 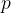 процентов, получим
процентов, получим

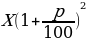
6. Если величину 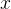 дважды уменьшить на
дважды уменьшить на 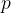 процентов, получим
процентов, получим

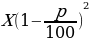
Затем мы применяем эти формулы для решения задач из профильного ЕГЭ.
1. В 2021 году в городском квартале проживало 40 000 человек. В 2022 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2023 году на 9% по сравнению с 2022 годом. Сколько человек стало проживать в квартале в 2023 году?
Решение.
По условию, в 2022 году число жителей выросло на 8%, то есть стало равно 40000 · 1,08, а в 2023 году число жителей выросло на 9%, теперь уже по сравнению с 2022 годом, значит в 2024 году в квартале стало проживать 40000 · 1,08 · 1,09 = 47088 жителей.
Ответ: 47 088.
2. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение.
Пусть при открытии торгов в понедельник акции стоили х рублей.
К вечеру понедельника они подорожали на р % и стали стоить 
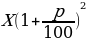
Теперь уже эта величина принимается за 100%, и к вечеру вторника акции подешевели на р% по сравнению этой величиной. По условию, акции в итоге подешевели на 4%. Получаем, что 
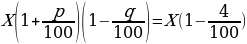
Поделим обе части уравнения на х (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения.
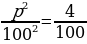
По смыслу задачи, величина р положительна.
Получаем, что р = 20.
Ответ: Подорожали на 20%.
На решение таких задач уходит много времени, поэтому я предлагаю учащимся дома ознакомиться с условием задачи, которую мы будем решать на следующем занятии и наметить план решения. А уже затем мы вместе обсуждаем предложения и идеи учащихся, учимся искать нужную информацию в тексте, аргументировать свою точку зрения. Разбираем, какие ошибки допущены в решении, какие можно было допустить и каким образом не допустить этих ошибок, обсуждаем возможности решения другими способами.
Я заметила, что большую часть экономических заданий составляют банковские задачи на кредиты и вклады, а также начисление процентов.
Поэтому на своих занятиях перед решением таких задач мы рассматриваем основные понятия и формулы, которые используются в задачах. Также к отдельным задачам привожу дополнительную информацию, разъясняющую условие и способы решения задач.
Прежде чем браться за реальные задания ЕГЭ, рассмотрим – как вообще работает банк?
Доход банка образуется в виде разницы между процентом кредита и процентом вклада. Например, клиент банка положил на свой сберегательный счет 100 тысяч рублей под 10% годовых – то есть открыл вклад. Через год он может получить в банке 100 · 1,1 = 110 тысяч рублей. Другому клиенту, наоборот, нужны 100 тысяч рублей. Банк выдает ему кредит под 30% годовых, и теперь этот клиент должен вернуть банку 100 · 1,3 = 130 тысяч рублей. Таким образом, прибыль банка составит 130 – 110 = 20 (тысяч рублей).
Конечно же, процентные ставки банка по кредиту выше, чем процентные ставки по вкладу.
Рассмотрим следующую задачу на кредиты.
В июле 2024 года планируется взять кредит на пять лет на сумму 1100 тыс. рублей. Условия его возврата таковы:
- каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
- в 2025, 2026 и 2027 годах сумма долга не изменяется;
- платежи в 2028 и в 2029 годах должны быть равны;
- к июлю 2029 года долг должен быть выплачен полностью.
На сколько рублей будут отличаться первый и последний платежи?
Мне удобнее при решении задач данного типа представить ситуацию, описанную в задаче и её моделирование с помощью таблицы.
Решение.
Кредит взят в июле 2024 года, то есть в этот год не производятся никакие выплаты и не начисляются проценты. Обозначим равные в 2028 и 2029 годах выплаты за S1 тыс. рублей.
По условию в 2025, 2026 и 2027 годах долг остается равным S = 1100 тыс. рублей.
Составим таблицу на основе этих данных:
| Год | Долг до начисления % | Долг после начисления % | Платеж | Сумма долга после выплаты |
| 2025 | S | 1,2 S | 0,2 S | S |
| 2026 | S | 1,2 S | 0,2 S | S |
| 2027 | S | 1,2 S | 0,2 S | S |
| 2028 | S | 1,2 S | S1 | 1,2S - S1 |
| 2029 | 1,2S - S1 | 1,2(1,2S - S1) | S1 | 1,2(1,2S - S1) - S1 |
По условию задачи долг был погашен полностью, значит,
1,2(1,2S - S1) - S1 = 0 → S1 = 36/55 S
Первый платеж был равен 0,2S, а последний был равен 36/55 S, значит, их разность равна
36/55 S - 0,2S = 500 (по условию S = 1100)
500 000р
1,2(1,2S – S1) - S1 = 0
Я познакомила вас только с некоторыми методическими приемами по решению экономических задач. На уроках математики я решаю простые экономические задачи, что помогает более эффективно на занятиях элективного курса решать задачи более сложного уровня. К сожалению за 15 минут невозможно поделиться всем тем, что я использую на своем элективном курсе.