Движение. Насретдинова Алина

ДВИЖЕНИЕ

РАБОТУ ВЫПОЛНИЛА

ученица 11 «А» класса

МБОУ СШ №75

города Ульяновска

Насретдинова Алина

Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.

Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.

Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.

ГЕРМАН ВЕЙЛЬ О СИММЕТРИИ

Движение в пространстве определяется так же, как и на плоскости

ДВИЖЕНИЕ – преобразование, при котором сохраняются расстояния между точками

Под движением пространства понимается отображение пространства на себя, при котором любые две точки А и В переходят (отображаются) в некие точки А 1 и В 1 так, что | АВ |=| А 1 В 1 |.

Иными словами, движение пространства – это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения плоскости, доказывается, что:

ПРИ ДВИЖЕНИИ В ПРОСТРАНСТВЕ:

• Прямые переходят в прямые
• Полупрямые – в полупрямые
• Отрезки – в отрезки
• Сохраняются углы между прямыми

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением

ОСНОВНЫЕ ТЕОРЕМЫ О ЗАДАНИИ ДВИЖЕНИЙ ПРОСТРАНСТВА:

ТЕОРЕМА 1. Пусть в пространстве даны два равных треугольника ABC и A'B'C'. Тогда существуют два и только два таких движения пространства, которые переводят A в A' , B в B' , C в C' . Каждое из этих движений получается из другого с помощью композиции его с отражением в плоскости A'B'C'

A

A'

С

В

C'

B'

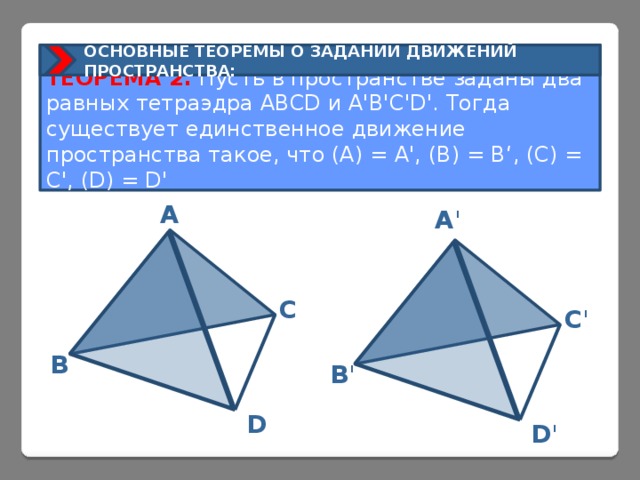
ОСНОВНЫЕ ТЕОРЕМЫ О ЗАДАНИИ ДВИЖЕНИЙ ПРОСТРАНСТВА:

ТЕОРЕМА 2. Пусть в пространстве заданы два равных тетраэдра ABCD и A'B'C'D'. Тогда существует единственное движение пространства такое, что (A) = A', (B) = B‘, (C) = C', (D) = D'

A

A '

С

С '

В

В '

D

D '

НЕПОДВИЖНЫЕ ТОЧКИ ДВИЖЕНИЙ ПРОСТРАНСТВА

Важной характеристикой движения пространства является множество его неподвижных точек. Здесь могут представиться лишь следующие случаи:

• У движения неподвижных точек нет (нетождественный параллельный перенос)
• Движение имеет лишь одну неподвижную точку (центральная симметрия)
• Множество неподвижных точек движения пространства является прямой (поворот вокруг прямой)
• Множество неподвижных точек движения пространства является плоскостью (зеркальная симметрия)
• Множество неподвижных точек движения пространства является всем пространством (тождественное движение)

ВИДЫ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ:

Центральная симметрия

(симметрия относительно точки):

А

D`

С

В`

В

С`

D

А`

ВИДЫ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ:

Осевая симметрия

(симметрия относительно прямой):

А

А`

С

D`

В

В`

D

С `

ВИДЫ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ:

Зеркальная симметрия (симметрия относительно плоскости):

D

С

А

В

А`

С `

В`

D`

ВИДЫ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ:

Параллельный перенос

(точки переносятся на данный вектор):

А

А`

С

В

С `

D

В`

D`

ВИДЫ ДВИЖЕНИЯ В ПРОСТРАНСТВЕ:

Поворот на данный угол вокруг данной точки:

А

А`

С `

С

В

В`

D`

D

ПРЕОБРАЗОВАНИЕ ПОДОБИЯ:

Центральным подобием О и коэффициентом k ≠0 называется отображение пространства на себя, при котором каждая точка М переходит в такую точку М 1 , что ОМ 1 = k ОМ .

М 1

М

О

ОБРАТНОЕ УТВЕРЖДЕНИЕ И ПОНЯТИЕ ПОДОБИЯ:

• Любое преобразование подобия представляет собой результат последовательного выполнения движения и центрального подобия

• Два тела называются подобными, если существует такое преобразование подобия, при котором одно из них переходит в другое

СИММЕТРИЯ ВОКРУГ НАС (ПРИРОДА):

СИММЕТРИЯ ВОКРУГ НАС (АРХИТЕКТУРА):

СИММЕТРИЯ ВОКРУГ НАС (АРХИТЕКТУРА):

СИММЕТРИЯ ВОКРУГ НАС (ЭМБЛЕМА АВТОМОБИЛЯ):

СИММЕТРИЯ ЛИЦА И ОРГАНИЗМА ЧЕЛОВЕКА:

СИММЕТРИЯ ВОКРУГ НАС (ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ):

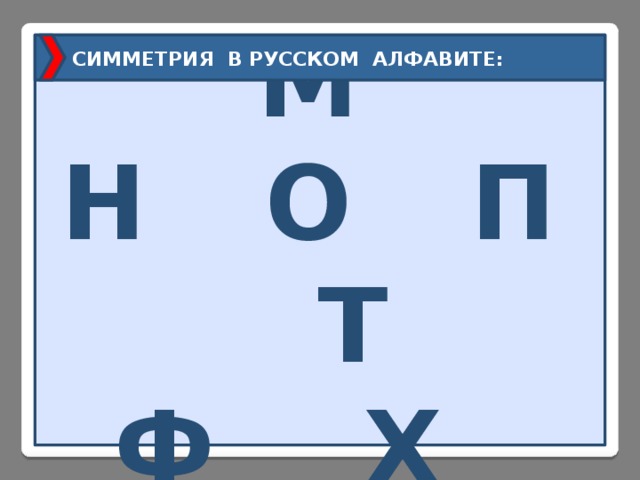
СИММЕТРИЯ В РУССКОМ АЛФАВИТЕ :

А Ж М

Н О П Т

Ф Х Ш

8 0

СИММЕТРИЯ ВОКРУГ НАС (ЦИФРЫ):

СИММЕТРИЯ ВОКРУГ НАС (ЖИВОТНЫЙ МИР):

СИММЕТРИЯ ВОКРУГ НАС (СИММЕТРИЯ В РАЗЛИЧНЫХ АГРЕГАТНЫХ СОСТОЯНИЯХ ВОДЫ):

СИММЕТРИЯ ВОКРУГ НАС (ЗЕРКАЛЬНОЕ ВРЕМЯ):

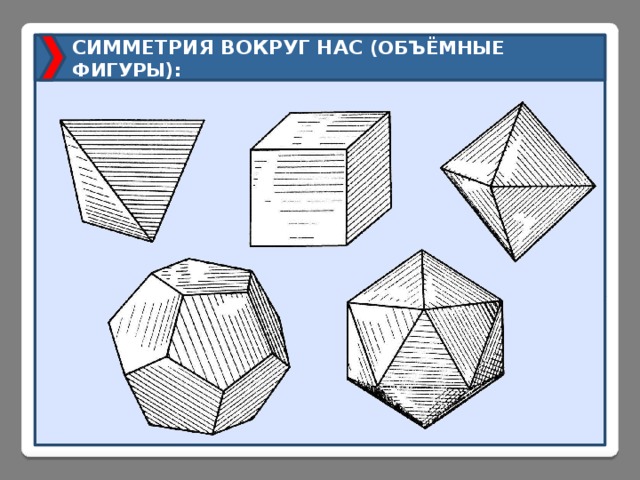
СИММЕТРИЯ ВОКРУГ НАС (ОБЪЁМНЫЕ ФИГУРЫ):

СИММЕТРИЯ ВОКРУГ НАС (ФЛАГИ ГОСУДАРСТВ):