РЕШУ ЕГЭ — информатика
Вариант № 17982114
1. Тип 1 № 63017 
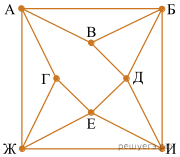
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что дорога АБ длиннее дороги ЖИ. Определите длину дороги ВД.
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | П8 |
| П1 | | | 8 | 11 | | 20 | | |
| П2 | | | 19 | 28 | | | 29 | 15 |
| П3 | 8 | 19 | | 12 | | | | 9 |
| П4 | 11 | 28 | 12 | | | 26 | | |
| П5 | | | | | | 18 | 16 | 14 |
| П6 | 20 | | | 26 | 18 | | 32 | |
| П7 | | 29 | | | 16 | 32 | | 17 |
| П8 | | 15 | 9 | | 14 | | 17 | |
2. Тип 2 № 63018 
Логическая функция F задаётся выражением:
((x → y) ∧ (z ≡ ¬w))→(u ≡ (x ∨ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
| ??? | ??? | ??? | ??? | ??? | F |
| 0 | | 0 | 0 | 0 | 0 |
| 0 | | | 0 | 0 | 0 |
| 0 | 0 | 0 | | 0 |
| 0 | | | 0 | 0 |
Определите, какому столбцу таблицы истинности соответствует каждая из переменных u, w, x, y, z.
В ответе напишите буквы u, w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть заданы выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности.
| Переменная 1 | Переменная 2 | Функция |
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 37481 
В файле приведён фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трёх таблиц.
3.xlsx
Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады июня 2021 г., а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок, шт. занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид.
| ID операции | Дата | ID магазина | Артикул | Тип операции | Количество упаковок,шт. | Цена,руб./шт. |
Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид.
| Артикул | Отдел | Наименование | Ед. изм. | Количествов упаковке | Поставщик |
Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид.
На рисунке приведена схема указанной базы данных.
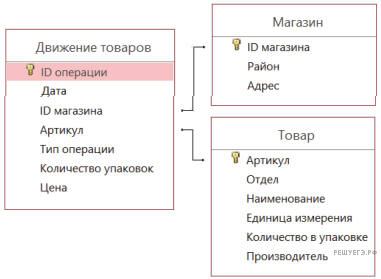
Используя информацию из приведённой базы данных, определите, сколько килограммов паштета из куриной печени было продано в магазинах Заречного района за период с 1 по 10 июня включительно.
В ответе запишите только число.
4. Тип 4 № 13616 
По каналу связи передаются сообщения, содержащие только пять букв: П, И, Л, О, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Для буквы И используется кодовое слово 1; для буквы О используется кодовое слово 01.
Какова минимальная общая длина кодовых слов для всех пяти букв?
Примечание. условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
5. Тип 5 № 18708 
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 85. В ответе запишите это число в десятичной системе счисления.
6. Тип 6 № 72564 
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять три команды: Вперёд n (n — число), Направо m (m — число) и Налево m (m — число). По команде Вперёд n Черепаха
перемещается вперёд на n условных единиц. По команде Направо m Черепаха поворачивается на месте на m градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения. По команде Налево m Черепаха поворачивается на месте на m градусов против часовой стрелки, при этом соответственно меняется направление дальнейшего движения. В начальный момент Черепаха находится в начале координат и направлена вверх (вдоль положительного направления оси ординат).
Запись Повтори k [Команда1 Команда2 ... КомандаS] означает, что заданная последовательность из S команд повторится k раз.
Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 23 Направо 90 Вперёд 10 Направо 90]
Вперёд 3 Налево 90 Вперёд 12 Направо 90
Повтори 2 [Вперёд 9 Направо 90 Вперёд 32 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор непересекающихся прямоугольников. Определите наибольшую из площадей этих прямоугольников. В ответе запишите только число — наибольшую площадь в условных единицах.
7. Тип 7 № 15919 
Автоматическая фотокамера производит растровые изображения размером 1600 на 1200 пикселей. При этом объём файла с изображением не может превышать 1 Мбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?
8. Тип 8 № 3228 
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
...
Укажите номер слова УАУАУ.
9. Тип 9 № 48430 
В каждой строке электронной таблицы записаны шесть натуральных чисел. Определите, сколько в таблице строк, для которых выполнены следующие условия:
— в строке встречается ровно четыре различных числа; два из них по два раза, два — по одному;
— сумма повторяющихся чисел (без учёта повторений, то есть каждое число входит в сумму один раз) меньше суммы неповторяющихся.
В ответе запишите число — количество строк, для которых выполнены эти условия.
Задание 9
10. Тип 10 № 51979 
Определите, сколько раз в тексте романа Михаила Булгакова «Мастер и Маргарита» встречается фамилия Лиходеев в начальной форме.
Задание 10
11. Тип 11 № 15981 
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 10 символов. Для построения идентификатора используют только прописные латинские буквы (26 букв). В базе данных для хранения каждого пароля отведено одинаковое минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым минимально возможным количеством бит. Кроме пароля для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено одинаковое целое количество байт на каждого пользователя. Для хранения информации о 15 пользователях потребовалось 300 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число — количество байт.
12. Тип 12 № 16890 
Исполнитель Редактор получает на вход строку цифр и преобразует её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 85 единиц?
НАЧАЛО
ПОКА нашлось (11111)
заменить (111, 2)
заменить (222, 1)
КОНЕЦ ПОКА
КОНЕЦ
13. Тип 13 № 13623 
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места — нули. Обычно маска записывается по тем же правилам, что и IP-адрес — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0. Для узла с IP-адресом 93.138.70.47 адрес сети равен 93.138.64.0. Каково наибольшее возможное общее количество единиц во всех четырёх байтах маски? Ответ запишите в виде десятичного числа.
14. Тип 14 № 19065 
Сколько единиц содержится в двоичной записи значения выражения: 48 + 28 − 8?
15. Тип 15 № 34542 
На числовой прямой даны два отрезка: P = [1, 39] и Q = [23, 58]. Какова наибольшая возможная длина интервала A, что логическое выражение
((x ∈ P) → ¬(x ∈ Q)) → ¬(x ∈ А)
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
16. Тип 16 № 4937 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(2) = 1;
F(n) = F(n – 2) · (n – 1) при n 2.
Чему равно значение функции F(7)? В ответе запишите только натуральное число.
17. Тип 17 № 58484 
Файл содержит последовательность натуральных чисел, не превышающих 20 000. Назовём парой два идущих подряд элемента последовательности.
Задание 17
Определите количество пар, для которых выполняются следующие условия:
— ровно одно число в паре четырёхзначное;
— сумма квадратов элементов пары без остатка делится на наименьшее в последовательности трёхзначное число, запись которого заканчивается цифрой 5.
В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар.
Ответ:
18. Тип 18 № 61364 
Робот стоит в левом верхнем углу прямоугольного поля, в каждой клетке которого записано целое положительное число. За один ход робот может переместиться на одну клетку вправо или на одну клетку вниз. Некоторые клетки выделены тёмным фоном. В эти клетки роботу заходить нельзя.
Клетка, из которой робот не может сделать допустимого хода (справа и снизу находятся границы поля или запрещённые клетки), называется финальной.
На поле может быть несколько финальных клеток.
В начальный момент робот обладает запасом энергии, которая расходуется на движение по клеткам. Расход энергии на прохождение каждой клетки, включая стартовую и финальную, равен числу, записанному в этой клетке.
Задание 18
Задание 1. Определите минимальный начальный запас энергии, который позволит роботу добраться до какой-нибудь финальной клетки.
Задание 2. Определите минимальный начальный запас энергии, который позволит роботу добраться до любой финальной клетки.
В обоих заданиях энергии должно хватить и на прохождение финальной клетки.
Исходные данные записаны в электронной таблице. В ответе запишите два числа: сначала ответ на задание 1, затем ответ на задание 2.
Ответ:
19. Тип 19 № 27844 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу три камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 13 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 49. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 50 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 49.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
20. Тип 20 № 27845 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу три камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 13 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 49. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 50 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 49.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите три таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания без разделительных знаков.
21. Тип 21 № 27846 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
добавить в кучу один камень, или
добавить в кучу три камня, или
увеличить количество камней в куче в два раза.
Например, имея кучу из 10 камней, за один ход можно получить кучу из 11, 13 или 20 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 49. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 50 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 49.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22. Тип 22 № 59815 
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Задание 22
Типовой пример организации данных в файле:
| ID процесса B | Время выполненияпроцесса B (мс) | ID процесса(ов) A |
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1; 2 |
| 4 | 7 | 3 |
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
23. Тип 23 № 63039 
Исполнитель преобразует число на экране.
У исполнителя есть три команды, которые обозначены буквами.
A. Вычесть 1.
B. Умножить на 2.
C. Умножить на 3.
Программа для исполнителя — это последовательность команд. Например, программа BAC при исходном числе 2 последовательно получит числа 4, 3, 9.
Сколько существует программ, которые преобразуют исходное число 3 в число 20 и при этом не содержат двух команд A подряд?
24. Тип 24 № 59702 
Текстовый файл состоит из символов T, U, V, W, X, Y и Z.
Определите в прилагаемом файле максимальное количество идущих подряд символов (длину непрерывной подпоследовательности), среди которых символ Y встречается не более 150 раз.
Для выполнения этого задания следует написать программу.
Задание 24
25. Тип 25 № 52196 
Маска числа — это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.
Пример. Маске 123*4?5 соответствуют числа 123405 и 12376415. Найдите все натуральные числа, не превышающие 109, которые соответствуют маске 12*93?1? и при этом без остатка делятся на 3127.
В ответе запишите все найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 59731 
Входной файл содержит сведения о заявках на проведение занятий в конференц-зале. В каждой заявке указаны время начала и время окончания мероприятия (в минутах от начала суток). Если время начала одного мероприятия меньше времени окончания другого, то провести можно только одно из них. Если время окончания одного мероприятия совпадает с временем начала другого, то провести можно оба. Определите какое максимальное количество мероприятий можно провести в конференц-зале и каков при этом максимальный перерыв между двумя последними мероприятиями.
Задание 26
Входные данные.
В первой строке входного файла находится натуральное число N (N ≤ 1000) — количество заявок на проведение мероприятий.
Следующие N строк содержат пары чисел, обозначающих время начала и время окончания мероприятий. Каждое из чисел натуральное, не превосходящее 1440.
Запишите в ответе два числа: максимальное — количество мероприятий и самый длинный перерыв между двумя последними мероприятиями (в минутах).
Ответ:
27. Тип 27 № 59705 
По каналу связи передаётся последовательность целых чисел — показания прибора. В течение N мин. (N — натуральное число) прибор ежеминутно регистрирует значение силы тока (в условных единицах) в электрической сети и передаёт его на сервер.
Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K мин., а сумма этих чисел была минимально возможной. Запишите в ответе найденную сумму.
Входные данные.
Файл А
Файл В
Даны два входных файла (файл A и файл B), каждый из которых в первой строке содержит натуральное число К — минимальное количество минут, которое должно пройти между моментами передачами любых двух из трёх показаний, а во второй — количество переданных показаний N (1 ≤ N 10 000 000, N K). B каждой из следующих N строк находится одно натуральное число, не превышающее 10 000 000, которое обозначает значение силы тока в соответствующую минуту.
Запишите в ответе два числа: сначала значение искомой величины для файла A, затем — для файла В.
Типовой пример организации данных во входном файле:
2
6
15
14
20
23
21
10
При таких исходных искомая величина равна 45 — это сумма значений, зафиксированных на первой, третьей и шестой минутах измерений.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Ответ:






























