

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 30.07.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

ЕГЭ 2025. Март Информатика Вариант 4
1. Тип 1 № 
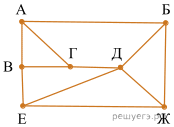
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Поскольку таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги АГ больше, чем длина дороги ВГ. Определите длину дороги БЖ. В ответе запишите целое число — длину дороги в километрах.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 10 | 7 | 8 | ||||
| 2 | 12 | 20 | 19 | ||||
| 3 | 10 | 12 | 14 | 15 | |||
| 4 | 7 | 9 | 11 | ||||
| 5 | 8 | 9 | 23 | ||||
| 6 | 20 | 14 | 11 | ||||
| 7 | 19 | 15 | 23 |
2. Тип 2 № 
Логическая функция F задаётся выражением:
(x → (y ≡ w)) ∧ (y ≡ (w → z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция
|
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 
В файле приведён фрагмент базы данных «Машины», принадлежащей союзу автодилеров, предлагающему покупателям автомобили. База данных состоит из трёх связанных прямоугольных таблиц.
Таблица «Наличие» содержит записи о поступивших дилеру и проданных покупателям машинах. Поле Тип операции содержит значение «Поступило дилеру» или «Отдано покупателю». Заголовок таблицы имеет вид:
| ID операции | Дата | ID машины | ID дилера | Количество | Тип операции |
Таблица «Марки» содержит информацию об автомобилях, продаваемых союзом автодилеров. Заголовок таблицы имеет вид:
| ID машины | Категория | Наименование |
Таблица «Дилеры» содержит информацию о местах расположения дилерских центров.
Заголовок таблицы имеет вид:
| ID дилера | Адрес | ФИО директора
|
На рисунке приведена схема указанной базы данных.
Используя информацию из приведённой базы данных, определите прирост количества отечественных автомобилей, завезенных в дилерские центры Москвы, имеющихся в наличии у дилеров на 01.01.2022 по сравнению с 01.01.2021.
В ответе запишите только число.
4. Тип 4 № 
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0.
Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наибольшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
5. Тип 5 № 
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления.
6. Тип 6 № 
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 6 [Направо 36 Вперёд 10 Направо 36].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7. Тип 7 № 
Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 224 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
8. Тип 8 № 
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?
9. Тип 9 № 
Откройте файл электронной таблицы, содержащей в каждой строке семь натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— среди семи чисел совпадают ровно четыре числа;
— среднее значение повторяющихся чисел строго меньше, чем среднее арифметическое ВСЕХ чисел строки.
В ответе запишите только число.
10. Тип 10 № 
Определите, сколько раз в сносках приложенного издания произведения А. С. Пушкина «Капитанская дочка» встречается слово «царский» в любой форме.
11. Тип 11 № 
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 13 символов, каждый из которых может быть одной из 12 допустимых заглавных букв или одной из 10 цифр. Для записи личного кода на пропуске отведено минимально возможное целое число байт. При этом используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит. Код подразделения состоит из двух трёхзначных чисел, каждое из которых кодируется как двоичное число и занимает минимально возможное целое число байт. Всего на пропуске хранится 32 байт данных. Сколько байт выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байт.
12. Тип 12 № 
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>0)
ЕСЛИ нашлось (>1)
ТО заменить (>1, 22>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>2)
ТО заменить (>2, 2>)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (>0)
ТО заменить (>0, 1>)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр 0, n цифр 1 и 39 цифр 2, расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
13. Тип 13 № 
В терминологии сетей TCP/IP маской подсети называется 32-разрядное двоичное число, определяющее, какие именно разряды IP-адреса компьютера являются общими для всей подсети, — в этих разрядах маски стоит 1. Обычно маски записываются в виде четверки десятичных чисел — по тем же правилам, что и IP-адреса. Для некоторой подсети используется маска 255.255.255.192. Сколько различных адресов компьютеров теоретически допускает эта маска, если два адреса (адрес сети и широковещательный) не используют?
14. Тип 14 № 
Значение выражения 3 · 2164 + 2 · 366 − 648 записали в системе счисления с основанием 6. Сколько цифр 5 содержится в этой записи?
15. Тип 15 № 
Сколько существует целых значений числа A, при которых формула
((x < A) → (x2 < 100)) ∧ ((y2 ≤ 64) → (y ≤ A))
тождественно истинна при любых целых неотрицательных x и y?
16. Тип 16 № 
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = F(n – 1) · F(n – 1) − F(n – 1) · n + 2 · n при n > 1.
Чему равно значение функции F(4)? В ответе запишите только натуральное число.
17. Тип 17 № 
Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 5 и хотя бы один из двух элементов меньше среднего арифметического всех элементов последовательности, значение которых нечетно. В ответе запишите два числа: сначала количество найденных пар, а затем — максимальную сумму элементов таких пар.
Например, в последовательности (8 10 2 9 5) есть две подходящие пары: (10 2) и (9 5), в ответе для этой последовательности надо записать числа 2 и 14.
Ответ:
18. Тип 18 № 
Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число было больше предыдущего. Какую максимальную сумму могут иметь выбранные числа?
В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана в виде одного столбца электронной таблицы.
Пример входных данных:
| 5,2 |
| 3,1 |
| 6,2 |
| 2,3 |
| 3,1 |
| 3,3 |
Для указанных входных данных максимально возможная сумма равна 9,3, в ответе надо записать число 9.
19. Тип 19 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите наименьшее значение S, при котором Петя не может выиграть за один ход, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом.
20. Тип 20 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
В ответе запишите найденные значения в порядке возрастания: сначала меньшее, затем большее.
21. Тип 21 № 
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней; 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Найдите наибольшее значение S, при котором у Пети есть выигрышная стратегия, позволяющая ему выиграть третьим ходом при любой игре Вани, но у Пети нет стратегии, которая позволяла бы ему гарантированно выиграть первым или вторым ходом.
22. Тип 22 № 
В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1
|
4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 
Исполнитель РазДваТри преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера.
1. Прибавить 1.
2. Умножить на 2.
3. Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья увеличивает на 3.
Программа для исполнителя РазДваТри — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 14 и при этом траектория вычислений не содержит чисел 5 и 10?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 312 при исходном числе 6 траектория будет состоять из чисел 9, 10, 20.
24. Тип 24 № 
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Определите количество строк, в которых буква A встречается чаще, чем буква E.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
25. Тип 25 № 
Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [1 000 000; 2 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 100. В ответе перечислите найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 
Предприятие производит оптовую закупку некоторых изделий A и B, на которую выделена определённая сумма денег. У поставщика есть в наличии партии этих изделий различных модификаций по различной цене. На выделенные деньги необходимо приобрести как можно больше изделий A независимо от модификации. Если у поставщика закончатся изделия A, то на оставшиеся деньги необходимо приобрести как можно больше изделий B. Известны выделенная для закупки сумма, а также количество и цена различных модификаций данных изделий у поставщика. Необходимо определить, сколько будет закуплено изделий B и какая сумма останется неиспользованной.
Входные данные.
Первая строка входного файла содержит два целых числа: N — общее количество партий изделий у поставщика и M — сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк описывает одну партию и содержит два целых числа (цена одного изделия в рублях и количество изделий в партии) и один символ (латинская буква A или B), определяющий тип изделия. Все данные в строках входного файла отделены одним пробелом.
В ответе запишите два целых числа: сначала количество закупленных изделий типа B, затем оставшуюся неиспользованной сумму денег.
Пример входного файла:
4 1000
30 8 A
50 12 B
40 14 A
30 60 B
В данном случае сначала нужно купить изделия A: 8 изделий по 30 рублей и 14 изделий по 40 рублей. На это будет потрачено 800 рублей. На оставшиеся 200 рублей можно купить 6 изделий B по 30 рублей. Таким образом, всего будет куплено 6 изделий B и останется 20 рублей. В ответе надо записать числа 6 и 20.
Ответ:
27. Тип 27 № 
В текстовом файле записан набор пар натуральных чисел, не превышающих 10 000. Необходимо выбрать из набора некоторые пары так, чтобы первое число в каждой выбранной паре было нечётным, сумма бо́льших чисел во всех выбранных парах была нечётной, а сумма меньших — чётной. Какую наибольшую сумму чисел во всех выбранных парах можно при этом получить?
Входные данные.
Первая строка входного файла содержит целое число N — общее количество пар в наборе. Каждая из следующих N строк содержит пару чисел.
Пример входного файла:
4
5 2
8 15
7 14
11 9 В данном случае есть три подходящие пары: (5, 2), (7, 14) и (11, 9). Пара (8, 15) не подходит, так как в ней первое число чётное. Чтобы удовлетворить требования, надо взять пары (7, 14) и (11, 9). Сумма бо́льших чисел в этом случае равна 25, сумма меньших равна 16. Общая сумма равна 41. В ответе надо указать число 41.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ:
Просмотр содержимого документа
«ЕГЭ 2025. Март Информатика Вариант 4»
1. Тип 1 № 28678 ![]()
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Поскольку таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги АГ больше, чем длина дороги ВГ. Определите длину дороги БЖ. В ответе запишите целое число — длину дороги в километрах.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 10 | 7 | 8 | ||||
| 2 | 12 | 20 | 19 | ||||
| 3 | 10 | 12 | 14 | 15 | |||
| 4 | 7 | 9 | 11 | ||||
| 5 | 8 | 9 | 23 | ||||
| 6 | 20 | 14 | 11 | ||||
| 7 | 19 | 15 | 23 |
2. Тип 2 № 48423 ![]()
Логическая функция F задаётся выражением:
(x → (y ≡ w)) ∧ (y ≡ (w → z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3. Тип 3 № 58318 ![]()
В файле приведён фрагмент базы данных «Машины», принадлежащей союзу автодилеров, предлагающему покупателям автомобили. База данных состоит из трёх связанных прямоугольных таблиц.
Задание 3
Таблица «Наличие» содержит записи о поступивших дилеру и проданных покупателям машинах. Поле Тип операции содержит значение «Поступило дилеру» или «Отдано покупателю». Заголовок таблицы имеет вид:
| ID операции | Дата | ID машины | ID дилера | Количество | Тип операции |
Таблица «Марки» содержит информацию об автомобилях, продаваемых союзом автодилеров. Заголовок таблицы имеет вид:
| ID машины | Категория | Наименование |
Таблица «Дилеры» содержит информацию о местах расположения дилерских центров.
Заголовок таблицы имеет вид:
| ID дилера | Адрес | ФИО директора |
На рисунке приведена схема указанной базы данных.
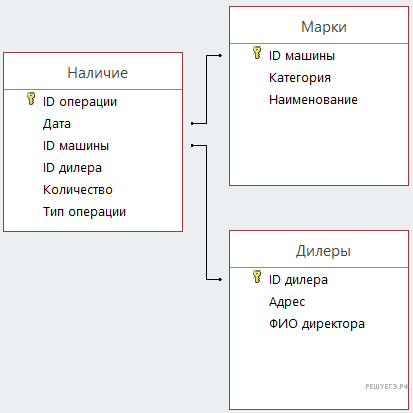
Используя информацию из приведённой базы данных, определите прирост количества отечественных автомобилей, завезенных в дилерские центры Москвы, имеющихся в наличии у дилеров на 01.01.2022 по сравнению с 01.01.2021.
В ответе запишите только число.
4. Тип 4 № 13562 ![]()
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0.
Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наибольшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование.
5. Тип 5 № 15846 ![]()
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа — результата работы данного алгоритма.
Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления.
6. Тип 6 № 47393 ![]()
Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм: Повтори 6 [Направо 36 Вперёд 10 Направо 36].
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
7. Тип 7 № 33477 ![]()
Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 224 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
8. Тип 8 № 7306 ![]()
Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?
9. Тип 9 № 59780 ![]()
Откройте файл электронной таблицы, содержащей в каждой строке семь натуральных чисел. Определите количество строк таблицы, содержащих числа, для которых выполнены оба условия:
— среди семи чисел совпадают ровно четыре числа;
— среднее значение повторяющихся чисел строго меньше, чем среднее арифметическое ВСЕХ чисел строки.
В ответе запишите только число.
Задание 9
10. Тип 10 № 47007 ![]()
Определите, сколько раз в сносках приложенного издания произведения А. С. Пушкина «Капитанская дочка» встречается слово «царский» в любой форме.
Задание 10
11. Тип 11 № 18494 ![]()
Каждый сотрудник предприятия получает электронный пропуск, на котором записаны личный код сотрудника, код подразделения и некоторая дополнительная информация. Личный код состоит из 13 символов, каждый из которых может быть одной из 12 допустимых заглавных букв или одной из 10 цифр. Для записи личного кода на пропуске отведено минимально возможное целое число байт. При этом используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством бит. Код подразделения состоит из двух трёхзначных чисел, каждое из которых кодируется как двоичное число и занимает минимально возможное целое число байт. Всего на пропуске хранится 32 байт данных. Сколько байт выделено для хранения дополнительных сведений об одном сотруднике? В ответе запишите только целое число — количество байт.
12. Тип 12 № 47216 ![]()
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (111, 27) преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка
исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Дана программа для Редактора:
НАЧАЛО
ПОКА нашлось (1) ИЛИ нашлось (2) ИЛИ нашлось (0)
ЕСЛИ нашлось (1)
ТО заменить (1, 22)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (2)
ТО заменить (2, 2)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (0)
ТО заменить (0, 1)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
На вход приведённой выше программе поступает строка, начинающаяся с символа «», а затем содержащая 39 цифр 0, n цифр 1 и 39 цифр 2, расположенных в произвольном порядке.
Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.
13. Тип 13 № 2237 ![]()
В терминологии сетей TCP/IP маской подсети называется 32-разрядное двоичное число, определяющее, какие именно разряды IP-адреса компьютера являются общими для всей подсети, — в этих разрядах маски стоит 1. Обычно маски записываются в виде четверки десятичных чисел — по тем же правилам, что и IP-адреса. Для некоторой подсети используется маска 255.255.255.192. Сколько различных адресов компьютеров теоретически допускает эта маска, если два адреса (адрес сети и широковещательный) не используют?
14. Тип 14 № 17380 ![]()
Значение выражения 3 · 2164 + 2 · 366 − 648 записали в системе счисления с основанием 6. Сколько цифр 5 содержится в этой записи?
15. Тип 15 № 15113 ![]()
Сколько существует целых значений числа A, при которых формула
((x A) → (x2 y2 ≤ 64) → (y ≤ A))
тождественно истинна при любых целых неотрицательных x и y?
16. Тип 16 № 4644 ![]()
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = F(n – 1) · F(n – 1) − F(n – 1) · n + 2 · n при n 1.
Чему равно значение функции F(4)? В ответе запишите только натуральное число.
17. Тип 17 № 40992 ![]()
Файл содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовём парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 5 и хотя бы один из двух элементов меньше среднего арифметического всех элементов последовательности, значение которых нечетно. В ответе запишите два числа: сначала количество найденных пар, а затем — максимальную сумму элементов таких пар.
Задание 17
Например, в последовательности (8 10 2 9 5) есть две подходящие пары: (10 2) и (9 5), в ответе для этой последовательности надо записать числа 2 и 14.
Ответ:
18. Тип 18 № 33097 ![]()
Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число было больше предыдущего. Какую максимальную сумму могут иметь выбранные числа?
В ответе запишите только целую часть максимально возможной суммы. Исходная последовательность записана в виде одного столбца электронной таблицы.
Задание 18
Пример входных данных:
| 5,2 |
| 3,1 |
| 6,2 |
| 2,3 |
| 3,1 |
| 3,3 |
Для указанных входных данных максимально возможная сумма равна 9,3, в ответе надо записать число 9.
19. Тип 19 № 47016 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите наименьшее значение S, при котором Петя не может выиграть за один ход, но у Пети есть выигрышная стратегия, позволяющая ему выиграть вторым ходом.
20. Тип 20 № 47017 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите два значения S, при которых у Вани есть выигрышная стратегия, позволяющая ему выиграть вторым ходом при любой игре Пети, но у Вани нет стратегии, которая позволяла бы ему гарантированно выиграть первым ходом.
В ответе запишите найденные значения в порядке возрастания: сначала меньшее, затем большее.
21. Тип 21 № 47018 ![]()
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень, добавить два камня или увеличить количество камней в куче в два раза. При этом нельзя повторять ход, который этот же игрок делал на предыдущем ходу. Повторять чужие ходы и свои более старые ходы разрешается.
Например, если в начале игры в куче 3 камня, Петя может первым ходом получить кучу из 4, 5 или 6 камней. Если Петя получил кучу из 5 камней (добавил два камня), то следующим ходом Ваня может получить 6, 7 или 10 камней. Если Ваня добавил один камень и получил 6 камней, то вторым ходом Петя может получить 7 или 12 камней. Получить 8 камней Петя не может, так как для этого нужно добавить 2 камня, а Петя делал это на предыдущем ходу.
Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней; 1 ⩽ S ⩽ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Найдите наибольшее значение S, при котором у Пети есть выигрышная стратегия, позволяющая ему выиграть третьим ходом при любой игре Вани, но у Пети нет стратегии, которая позволяла бы ему гарантированно выиграть первым или вторым ходом.
22. Тип 22 № 47600 ![]()
В файле 22_19.xlsx содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно.
Информация о процессах представлена в файле в виде таблицы. В первой строке таблицы указан идентификатор процесса (ID), во второй строке таблицы — время его выполнения в миллисекундах, в третьей строке перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
| ID процесса B | Время выполнения процесса B (мс) | ID процесса(ов) A |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 3 | 0 |
| 3 | 1 | 1;2 |
| 4 | 7 | 3 |
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 — через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
23. Тип 23 № 16898 ![]()
Исполнитель РазДваТри преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера.
1. Прибавить 1.
2. Умножить на 2.
3. Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья увеличивает на 3.
Программа для исполнителя РазДваТри — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 14 и при этом траектория вычислений не содержит чисел 5 и 10?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 312 при исходном числе 6 траектория будет состоять из чисел 9, 10, 20.
24. Тип 24 № 33103 ![]()
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Определите количество строк, в которых буква A встречается чаще, чем буква E.
Для выполнения этого задания следует написать программу. Ниже приведён файл, который необходимо обработать с помощью данного алгоритма.
Задание 24
25. Тип 25 № 33197 ![]()
Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [1 000 000; 2 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 100. В ответе перечислите найденные числа в порядке возрастания.
Ответ:
26. Тип 26 № 33528 ![]()
Предприятие производит оптовую закупку некоторых изделий A и B, на которую выделена определённая сумма денег. У поставщика есть в наличии партии этих изделий различных модификаций по различной цене. На выделенные деньги необходимо приобрести как можно больше изделий A независимо от модификации. Если у поставщика закончатся изделия A, то на оставшиеся деньги необходимо приобрести как можно больше изделий B. Известны выделенная для закупки сумма, а также количество и цена различных модификаций данных изделий у поставщика. Необходимо определить, сколько будет закуплено изделий B и какая сумма останется неиспользованной.
Входные данные.
Задание 26
Первая строка входного файла содержит два целых числа: N — общее количество партий изделий у поставщика и M — сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк описывает одну партию и содержит два целых числа (цена одного изделия в рублях и количество изделий в партии) и один символ (латинская буква A или B), определяющий тип изделия. Все данные в строках входного файла отделены одним пробелом.
В ответе запишите два целых числа: сначала количество закупленных изделий типа B, затем оставшуюся неиспользованной сумму денег.
Пример входного файла:
4 1000
30 8 A
50 12 B
40 14 A
30 60 B
В данном случае сначала нужно купить изделия A: 8 изделий по 30 рублей и 14 изделий по 40 рублей. На это будет потрачено 800 рублей. На оставшиеся 200 рублей можно купить 6 изделий B по 30 рублей. Таким образом, всего будет куплено 6 изделий B и останется 20 рублей. В ответе надо записать числа 6 и 20.
Ответ:
27. Тип 27 № 36001 ![]()
В текстовом файле записан набор пар натуральных чисел, не превышающих 10 000. Необходимо выбрать из набора некоторые пары так, чтобы первое число в каждой выбранной паре было нечётным, сумма бо́льших чисел во всех выбранных парах была нечётной, а сумма меньших — чётной. Какую наибольшую сумму чисел во всех выбранных парах можно при этом получить?
Входные данные.
Файл A
Файл B
Первая строка входного файла содержит целое число N — общее количество пар в наборе. Каждая из следующих N строк содержит пару чисел.
Пример входного файла:
4
5 2
8 15
7 14
11 9 В данном случае есть три подходящие пары: (5, 2), (7, 14) и (11, 9). Пара (8, 15) не подходит, так как в ней первое число чётное. Чтобы удовлетворить требования, надо взять пары (7, 14) и (11, 9). Сумма бо́льших чисел в этом случае равна 25, сумма меньших равна 16. Общая сумма равна 41. В ответе надо указать число 41.
Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла A, затем для файла B.
Ответ:
Полезное для учителя












Видеоуроки по информатике 6 класс (к...
Электронная тетрадь по информатике 6...
Информатика 7 класс ФГОС
Информатика и ИКТ 11 класс (к учебнику...
Информатика 4 класс ФГОС
Информатика 9 класс ФГОС
Электронная тетрадь по информатике 8...
Основы алгоритмизации и...
© 2025, Петриашвили Ирина Николаевна 183 0
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы