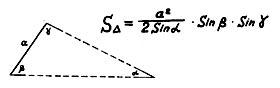Его величество, треугольник!

Муниципальное образовательное учреждение

«Средняя общеобразовательная школа № 152»

Учебно-познавательный проект

Автор: Фесенко Нина Николаевна

Классный руководитель 10 класса

Омск

2010-2011 учебный год

ВВЕДЕНИЕ

Актуальность проекта

Треугольник – одна из простейших фигур геометрии. Так ли это? Есть у треугольника еще какие-нибудь тайны? Зачем треугольники в жизни?

Это одна из первых и самых важных тем в геометрии. Действительно, от глубокого ее изучения зависят дальнейшие успехи в геометрии. Практически ни один урок геометрии не обходится без обращения к треугольнику, его свойствам, формулам, связанным с этой фигурой. Особенно остро это ощущается при подготовке выпускников к ЕГЭ по математике. Идёт тенденция увеличения количества геометрических задач в КИМах и ни одна из них не обходится без прямого или косвенного присутствия треугольников. Но треугольники имеют интерес не только в учебном смысле. Первый треугольник, который человек встречает в жизни, называется папа-мама-я. Три вершинки, три ниточки между членами семьи – и вот уже первый в жизни треугольник готов.

Этим проектом я хочу подчеркнуть важность темы, развить интерес ребят к предмету, научить получать удовольствие от самостоятельного поиска знаний, увидеть связь между наукой и жизнью.

Цель, гипотеза и задачи проекта

Цель: Формирование учебной мотивации, познавательного интереса, расширение кругозора.

Гипотеза: От того, как сформирован интерес школьника к какой-либо теме, зависит его успешность, желание укреплять и совершенствовать свои знания. Предполагается, что работа по формированию интереса к изучению треугольников через участие в данном проекте учащимися 10 класса будет способствовать повышению уровня знаний, поможет посмотреть на геометрию с другой стороны (ни как на скучный предмет), увидеть связь с жизнью и повысить свой общекультурный уровень

Задачи: 1. Включить учащихся в активную деятельность, в проживание реальных событий и чувств, позволяющих ученику осмыслить социальную и личностную значимость этой деятельности и ее результатов, оценить свои склонности и возможности в выполнении деятельности.

2. Стимулировать интерес учащихся к собственному приобретению знаний из разных областей и источников, которые могут быть использованы в жизни, в будущей профессиональной деятельности.

3. Формировать ключевые умения и компетенции:

• проектировочные: определение цели, планирование работы и распределение обязанностей, реализация проекта, оформление результатов, общественная презентация, рефлексия;

• познавательные; навыки самостоятельной работы с информацией, самостоятельного конструирования знаний;

• исследовательские: выявление проблем, сбор информации, обобщение;

• коммуникативные: передача информации, умение слушать и понимать другого;

• социальные: умение сотрудничать в групповом общении и принятии решений, принимать собственные решения и брать за них на себя ответственность, регулировать конфликты;

• информационные: владение способами получения информации из разных источников, в том числе Интернет-ресурсов, обработка информации и хранение.

Этапы реализации проекта

Проект среднесрочный. Сроки реализации: март-май

Первый этап. Предварительная работа.

Учитель задаёт план работы над проектом:

• организует его обсуждение,

• класс разбивается на 3 группы по 3-4 человека (временные творческие объединения, в каждой группе выбирают ответственного, распределяются обязанности):

Второй этап. Коллективное планирование. Ученики высказывают свои предложения относительно способов реализации проекта и продукта на выходе, возможные способы оформления (доклад, реферат, сценарий, газета, книга, альбом, презентация, модель, макет, рисунок, сочинение)

Третий этап. Сбор, анализ и обобщение информации из разных источников.

Учитель предлагает учащимся выбрать способ сбора и оформления результатов проектной деятельности и способ их презентации, исходя из интересов, желания и возможностей учащихся и школы, а также целесообразности с точки зрения особенностей материала проекта и его значимости.

Четвёртый этап. Проведение коллективного творческого дела:

-Изучение учебного теоретического материала, его систематизация и обобщение в виде памятки-раскладушки по теме «треугольники»

-Сбор материала по теме «Треугольники в архитектуре», создание альбома с фотографиями.

-Сбор материала по теме «Треугольники в жизни человека» (Здоровье, психология и т.п.) – сообщение в виде реферата.

-тестирование (тест психологическая геометрия)

Пятый этап. Рефлексия.

Учитель предлагает группам дать самооценку качества проекта, его соответствия цели и гипотезе.

• процесса работы над проектом оптимальности и продуктивности работы, затруднений и способы преодоления;

• качество сотрудничества членов группы: взаимопомощи, и вклада ответственности каждого за общий успех.

• личностных достижений: влияния работы над проектом на мотивацию учения, волевые качества, навыки самообразования, коммуникативные способности, кругозор, уверенность в себе и удовлетворенность работой и собственными достижениями.

Учитель, в свою очередь, оценивает удачные и неудачные моменты в своей деятельности по педагогическому руководству проектной деятельностью детей. Совместно с детьми решают, какие усовершенствования в эту работу внести

Приложение (содержание деятельности)

1. Обобщение теоретического учебного материала по теме «Треугольник»

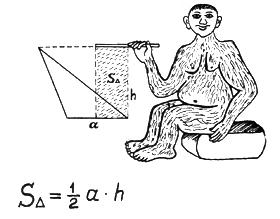
Площадь треугольника по основанию и высоте

Площадь треугольника
знали предки те,
что пол основания
брать по высоте.

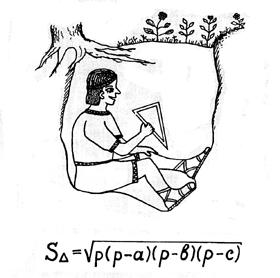
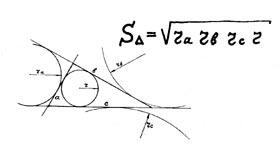
Формула Герона (площадь треугольника по трем сторонам)

Герон полупериметр
под корень затащил,
Три раза перемножил
и площадь получил.

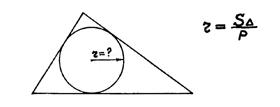
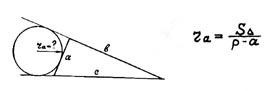
Радиус вписанной в треугольник окружности

Если площадь треугольника
на полупериметр разделить,
то самый малый радиус
нетрудно получить.

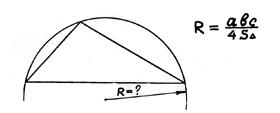
Радиус описанной около треугольника окружности

Как радиус побольше
аbс-олютно сбыть?
На четыре площади
надо разделить.

Радиусы внешние

И радиусы внешние
будут нам видны,
когда разделим площадь
на полупериметр
без этой стороны.

Площадь треугольника по четырем радиусам

Все радиусы внешние
и внутренний один
для вычисленья площади
под корень поместим.

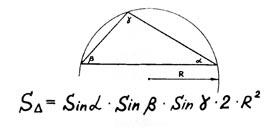
Площадь треугольника по углам и радиусу описанной окружности

Мы площадь треугольника
запишем в длинный ряд,
перемножив синусы
на два, на "эр-квадрат".

Площадь треугольника по одной стороне и трем углам

"А-в-квадрате" разделяем
на два синуса своих
и еще перемножаем
на два синуса других.

Свойства высот  треугольника 

1. В прямоугольном  треугольнике  высота, проведенная из вершины прямого угла, разбивает его на два  треугольника , подобные исходному  треугольнику .

2. В остроугольном  треугольнике  две его высоты отсекают от него подобные  треугольники .

3. Если  треугольник  остроугольный, то все основания высот принадлежат сторонам  треугольника, а у тупоугольного  треугольника  две высоты попадают на продолжение сторон.

4. Три высоты в остроугольном  треугольнике  пересекаются в одной точке и эту точку называют ортоцентром  треугольника.

Медиана

Медианы (от лат. mediana – «средняя») – это отрезки, соединяющие вершины  треугольника  с серединами противолежащих сторон (см. рис. 3).

Для построения медианы необходимо выполнить следующие действия:

1) найти середину стороны;

2)соединить точку, являющуюся серединой стороны  треугольника , с противолежащей вершиной отрезком.

Свойства медиан  треугольника 

1. Медиана разбивает  треугольник  на два  треугольника  одинаковой площади.

2. Медианы  треугольника  пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Весь  треугольник  разделяется своими медианами на шесть равновеликих  треугольников.

Биссектриса

Биссектрисами (от лат. bis – дважды» и seko – рассекаю) называют заключенные внутри  треугольника  отрезки прямых, которые делят пополам его углы (см. рис. 4).

Для построения биссектрисы необходимо выполнить следующие действия:

1) построить луч, выходящий из вершины угла и делящий его на две равные части (биссектрису угла);

2) найти точку пересечения биссектрисы угла  треугольника  с противоположной стороной;

3) выделить отрезок, соединяющий вершину  треугольника  с точкой пересечения на противоположной стороне.

Свойства биссектрис  треугольника 

1. Биссектриса угла  треугольника  делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.

2. Биссектрисы внутренних углов  треугольника  пересекаются в одной точке. Это точка называется центром вписанной окружности.

3. Биссектрисы внутреннего и внешнего углов перпендикулярны.

4. Если биссектриса внешнего угла  треугольника  пересекает продолжение противолежащей стороны, то ADBD=ACBC.

5. Биссектрисы одного внутреннего и двух внешних углов  треугольника  пересекаются в одной точке. Эта точка — центр одной из трех вневписанных окружностей этого  треугольника .

6. Основания биссектрис двух внутренних и одного внешнего углов  треугольника  лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне  треугольника .

7. Если биссектрисы внешних углов  треугольника  не параллельны противоположным сторонам, то их основания лежат на одной прямой.

Средняя линия

Средние линии - это отрезки, соединяющие середины двух сторон.

Для построения средней линии необходимо выполнить следующие действия:

1) найти середины двух сторон  треугольника ;

2) соединить середины сторон отрезком (см. рис.5).

Три средние линии  треугольника  образуют «вписанный» в него  треугольник , называемый серединным. Его площадь в четыре раза меньше площади данного  треугольника 

ВИДЫ  ТРЕУГОЛЬНИКОВ 

Существует две классификации  треугольников : по углам и сторонам

Классификация по углам

Определение.  Треугольник  называется остроугольным, если все три его

угла — острые, то есть меньше 90°.

Определение.  Треугольник  называется тупоугольным, если один из его

углов — тупой, то есть больше 90°.

Определение.  Треугольник  называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного  треугольника , противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.

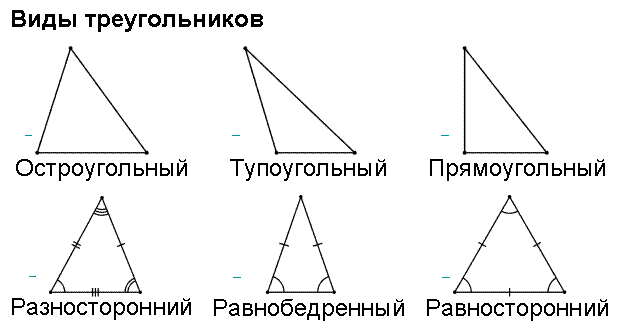
Классификация по сторонам

Определение.  Треугольник  называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием  треугольника .

Определение.  Треугольник , у которого все стороны равны, называется равносторонним или правильным.

РАВНОБЕДРЕННЫЙ  ТРЕУГОЛЬНИК 

Определение. Равнобедренный  треугольник  —  треугольник , в котором две стороны равны между собой. По определению, правильный  треугольник  также является равнобедренным, но обратное, вообще говоря, неверно (см. рис. 9).

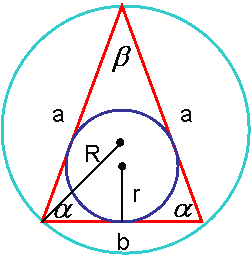
a — длина двух равных сторон равнобедренного  треугольника ,

b — длина третей стороны,

α и β — соответствующие углы,

R — радиус описанной окружности,

r — радиус вписанной окружности.

Свойства

1. Углы, противолежащие равным сторонам равнобедренного  треугольника , равны между собой.

2. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

3. Биссектриса, медиана и высота, проведенные к основанию совпадают между собой.

4. Центры вписанной и описанной окружностей лежат на этой линии.

5. Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).

Признаки

1. Два угла  треугольника  равны.

2. Высота совпадает с медианой.

3. Высота совпадает с биссектрисой.

4. Биссектриса совпадает с медианой.

РАВНОСТОРОННИЙ  ТРЕУГОЛЬНИК 

Определение. Правильный  треугольник  или равносторонний  треугольник  — правильный многоугольник с тремя сторонами. Все стороны равны между собой, и все углы равны 60° (или π / 3) (см. рис. 10).

t — сторона правильного  треугольника ,

R — радиус описанной окружности,

r — радиус вписанной окружности.

Свойства

1. Каждая из высот является одновременно биссектрисой и медианой.

2. Центры описанной и вписанной окружностей совпадают.

ПРЯМОУГОЛЬНЫЙ  ТРЕУГОЛЬНИК 

Определение.  Треугольник  называют прямоугольным, если у него есть прямой угол.

Свойства

1. Прямоугольный  треугольник  имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).

2. Сумма двух острых углов прямоугольного  треугольника  равна прямому углу.

3. Две высоты прямоугольного  треугольника  совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла  треугольника .

4. Центр описанной окружности прямоугольного  треугольника  лежит в середине гипотенузы.

5. Медиана прямоугольного  треугольника , проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого  треугольника  окружности.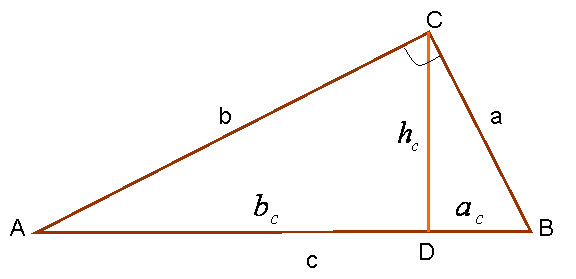

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного  треугольника .

Геометрическая формулировка. В прямоугольном  треугольнике  площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном  треугольнике  квадрат гипотенузы равен сумме квадратов катетов. То есть, обозначив длину гипотенузы  треугольника  через c, а длины катетов через a и b: a² + b² = c².

Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный  треугольник  с катетами a и b и гипотенузой c.

Признаки равенства прямоугольных  треугольников :

1. по катету и гипотенузе;

2. по двум катетам;

3. по катету и острому углу;

4. по гипотенузе и острому углу.

ПРИЗНАКИ РАВЕНСТВА И ПОДОБИЯ ТРЕУГОЛЬНИКОВ

ПРИЗНАКИ РАВЕНСТВА  ТРЕУГОЛЬНИКОВ

Первый признак равенства  треугольников .

Если две стороны и угол между ними одного  треугольника  равны соответственно двум сторонам и углу между ними другого  треугольника, то такие  треугольники  равны

ΔABC=Δ DEF по двум сторонам и углу между ними

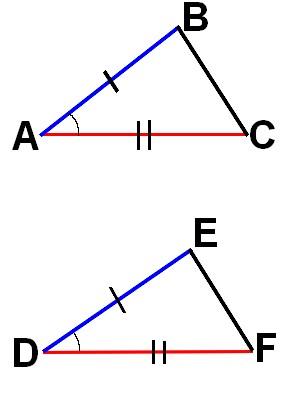
Второй признак равенства  треугольников .

Если сторона и прилежащие к ней углы одного  треугольника  равны соответственно стороне и прилежащим к ней углам другого  треугольника , то такие  треугольники  равны (см. рис. 13.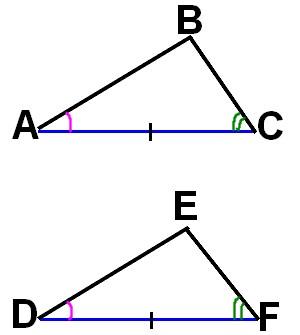

ΔABC=ΔDEF по стороне и прилежащим к ней углам.

Третий признак равенства  треугольников 

Если три стороны одного  треугольника  равны соответственно трем сторонам другого  треугольника , то такие  треугольники  равны. (см. рис. 14

ПРИЗНАКИ ПОДОБИЯ  ТРЕУГОЛЬНИКОВ 

Первый признак

Два  треугольника  подобны, если два угла одного  треугольника  соответственно равны двум углам другого  треугольника  (см. рис. 15).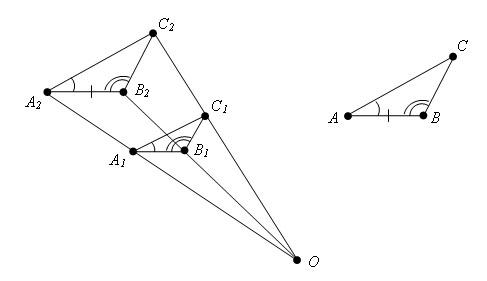

Второй признак

Два  треугольника  подобны, если две стороны одного  треугольника  пропорциональны двум сторонам другого и углы, образованные этими сторонами в этих  треугольниках , равны (см. рис. 16).

Третий признак

Два  треугольника  подобны, если три стороны одного  треугольника  пропорциональны сторонам другого  треугольника  (см. рис. 17).

Прямоугольные  треугольники  подобны, если гипотенуза и катет одного  треугольника  пропорциональны гипотенузе и катету другого  треугольника.

2. Стихи  о   треугольнике 

 О,  треугольник, как ты прекрасен.

Как красив и богат,

Ибо ты имеешь три стороны.

Три угла, три вершины.

Ты один можешь быть:

И равнобедренным, и равносторонним,

И прямоугольным…

Ибо ты могуч…

…По тебе судят теоремы,

Тебе посвятили три признака равенства.

Ведь, чтобы доказать, что ты равен,

Нужно приложить силы.

Ибо даже медиана, проведенная

К основанию равнобедренного  треугольника 

Является высотой и биссектрисой.

И не каждый  знает , что в  треугольнике 

Медианы, высоты, биссектрисы

Пересекаются в одной точке.

И что бы  мы   знали  без Великого  треугольника !

Ибо даже стол не может стоять на двух ножках.

Ода  треугольнику  в стихах.

Вы всем известны,

Без вас не обойтись нигде,

Вы так чудесны,

Вы так нужны везде.

Вы - Геометрические фигуры,

 Треугольники  мои.

“ Треугольник ,  треугольник ”.

Самый лучший из фигур,

Ты родился из трех точек

И прекрасных трех прямых.

Но не думайте, ребята,

 Треугольник  не простой…

Он бывает и прямой,

Равнобедренный…любой!!!

О медиане и …

Медиана – она мышка Яна,

Зацепившись хвостом за вершину,

Спустилась к основанию

Прямо в середину!

Высота стоит столбом – вертикально.

Она измерит даже дом капитально.

Биссектриса - почему так назвали, не пойму…

Потому что, потому

Она ходит по углам

И делит угол пополам.

Биссектриса – это киска,

Которая ловит мышку по углам,

И делит угол пополам!

Медианка – хулиганка

Бросит вещи по углам и

Стороны делит пополам

В  треугольнике  она стоит

Прямо – как всегда.

Высота, высота!

С высоты глядит на нас:

“С медианой ты не путай,

Есть ведь разница у нас”.

Медиана – как лиана,

Только разница одна –

Из вершины в середину

Не промахнется никогда.

Ода признакам  треугольников 

 О ,  треугольники , вы так прекрасны,

Три признака ваши для нас не сложны.

Вот первый из них:

Если две стороны и угол между ними

Одного  треугольника  равны

Двум сторонам и углу между ними другого  треугольника ,

То такие  треугольники  равны.

А теперь будьте умны…

Приставьте числительные одна и два

К словам “сторона” и “угла”

И пред ваши очи вмиг

Второй признак подбежит.

А у третьего признака нет углов,

А только три стороны равны.

Третий признак легче всех.

Ну, а вы, мной ободрены,

Додумайте его непременно.

Вы отроки – други, запомните ныне

Сии признаки равенства  треугольников .

Итак, это  треугольник  с одной стороны.

1. Треугольники в архитектуре

История знаковой символики напрямую связана с развитием цивилизации, возникновением письменного изобразительного языка, его генезисом во времени и пространстве. Поэтому достаточно трудно с известной долей вероятности, оперируя разрозненными крупицами фактов тысячелетней давности, дать безусловное определение тому или иному символу. К тому же одни и те же изображения можно наблюдать у разных народов в различных частях света. Это относится, в первую очередь, к простым геометрическим фигурам, таким как треугольник, окружность, квадрат, крест и звезда.

В архитектурном декоре городов южнороссийского региона второй половины ХIХ – начала ХХ вв. нередко встречаются общезначимые геометрические формы.

Символ «треугольник». Треугольник служил одним из символов Земли. В христианстве же треугольник служил символом божества, "всевидящего ока". Поскольку в этом случае из треугольника исходят солнечные лучи, он здесь связан с символикой солнечного культа. В раннем средневековье треугольник стал символом Троицы, являясь языческим символом трех солнц.

В различных видах треугольник – обычный в архитектурном декоре орнаментальный мотив, особенно употребляемый в XIX – начале XX вв.

Новый проект застройки набережной г. Омска представила Группа компаний «Стройинвест».

Примерная стоимость строительства – 600 млн. рублей. На совете проект презентовал его архитектор – Владимир Паровышник. Вдоль набережной Тухачевского от ул. Фрунзе до ул. Кемеровская по задумке автора должны вырасти три высотных здания в виде треугольников на прямоугольной «платформе» - в ней можно расположить офисы и парковку. А от третьего здания «вырастает» еще и прямоугольная многоэтажка со скошенной под заточенный карандаш крышей. Все дома будут облицованы прозрачным стеклом.

Такая треугольная форма строений – это не только дань урбанистическому стилю. По словам г-на Паровышника, она была обусловлена требованиями инсталляции. Дело в том, что сразу за проектируемыми домами уже расположены четырнадцатиэтажки. Так вот «треугольники» не будут загораживать эти здания от солнца. В этом вопросе проектировщики все точно рассчитали. «Есть, правда, некоторая сложность – в нестандартных по форме зданиях нужно будет тщательно прорабатывать систему вентиляции и дымоудаления, - подытожил архитектор. - Но мы представляем только концепцию застройки района. Когда дело дойдет до проектирования, все эти вопросы будут решаться конкретно».

Но гораздо более непонятным для архитекторов стал вопрос эксплуатации зданий. Что же все-таки расположится в «треугольниках» - офисы, жилье или и то и другое – ни архитектор ни застройщик пояснить не смогли. Снова сослались на то, что это только концепция застройки. А между тем градостроители настаивали на четкой характеристике объектов. От этого зависит и количество парковочных мест и в целом развитие застраиваемой зоны. Пока же решили проект г-на Паровышника принять к сведению, а на проект застройки района объявить конкурс среди архитекторов.

СПРАВКА: Общая площадь застройки – 2300 кв. метров, парковка до 145 мест, если это будут жилые дома, и 240 – если офисы. Высота треугольных зданий – 71 метр. Прямоугольная высотка – выше 100 метров.

4.Треугольники в жизни

Загадки  треугольника 

С другой стороны  треугольник  это - тайный оккультный знак, встречающийся во многих цивилизациях. Три угла, три грани - магическое число 3. Не удивительно, что  треугольник  можно найти на тайных письменах, символах, пентаграммах. И совсем не удивительно, что самые загадочные места и строения могут быть связаны тоже с  треугольниками . Например, египетские пирамиды (в Египте  треугольник  символизировал триаду духовной воли, любви-интуиции и высшего разума человека, то есть его личность и душу.) Или звезда Давида (еврейский символ, образованный наложением двух  треугольников ). А еще Бермудский  треугольник .

Платон утверждал, что вообще вся “Поверхность состоит из  треугольников ”.
На самом деле  треугольники  используются везде и всюду. Уже со времён палеолита и неолита в древнем искусстве очень широко распространяются изображения равностороннего  треугольника . Первобытные люди покрывали сферические сосуды сетью круглых равносторонних  треугольников . Символическое изображение  треугольника  есть в архитектуре и строительстве (пирамиды и др.), во фрагментах одежды и украшениях. Вожди племен североамериканских индейцев носили на груди символ власти:
равносторонний  треугольник . В Африке женщины туарегов также украшали себя большими пластинами из равносторонних  треугольников .

Один из самых загадочных и интересных  треугольников  – “Бермудский  треугольник ”. Еще это место называют аномальной зоной.

Рис. 18

На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов - большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках не удалось обнаружить ни одного трупа или обломка.

Над океаном плыл рассвет.

Светлело небо, голубея.

Фелюга* шла к Бермудам, нет

Таинственней загадки, злее.

Проникнув в эпицентр Бермуд,

 мы  видим розу из тумана.

В ней тени кораблей плывут,

"Мэри Селест" без капитана.

Ворота в рай иль ад, не  знаем ,

но  мы  войдем туда сейчас.

Сиянье ширится, сгораем...

Не поминайте лихом нас.

Бермудский  треугольник  не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение - это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь - 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский  треугольник ” не является географическим.

Древние говорили, что Земля поделена на правильные  треугольники , а Платон заявлял, что “Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи”, т.е. 12 пентаграмм.

В свою очередь, каждая пентаграмма делится на  треугольники  большие и  треугольники  помельче. Таким образом, поверхность Земли предстает в виде в пересечении вершин  треугольников , в которых образуются “энергетические узлы”. Эта идея разработана русскими исследователями Н. Гончаровым, В. Морозовым и В. в соответствии с которой цивилизации развивались в “энергетических узлах”. В пересечении вершин  треугольников  образуются особенно богатые запасы полезных ископаемых, в некоторых “узлах” порой исчезают материальные предметы (Бермудский  треугольник ).

Треугольники в психологии

Тест

Эти тесты помогут тебе немножко разобраться в том, что какой ты человек.

Доволен ли ты собой

Перед тобой пять геометрических фигур: квадрат, прямоугольник, треугольник, круг, зигзаг. Выбери из них ту, которая тебе понравилась больше других. Выбрал? Тогда читай о себе!   Квадрат.  Ты человек работящий, старательный. Любое дело доводишь до конца. Любишь порядок, все вещи твои всегда на своих местах. Но иногда ты чрезмерно придирчива к другим.   Прямоугольник.  Ты интересный и любознательный человек. Довольно легко можешь усваивать новые знания. Вообще любишь все новое. Но иногда не знаешь, чего тебе хочется больше , не можешь выбрать главное.   Треугольник.  Ты человек целенаправленный. Тебя трудно удержать на пути к поставленной цели. Любишь командовать другими, но можешь неожиданно растеряться, если верховодить захочет другой человек.    Круг.  Ты доброжелательный человек. Любишь помогать другим, переживаешь за них. Конечно, твое сочувствие помогает, но лучше подумай, как помочь товарищу не только словом, но и делом.

Тест: психологическая геометрия

Всегда бывает крайне интересно узнать о себе что-то новенькое , что-то особенное и, тем более, приятное. Не менее интересно в одночасье понять основные черты характера близкого человека, или не очень близкого, но все равно интересно... Отчасти этим объясняется повальный интерес к психологии в последние годы. А психология, в свою очередь, охотно делиться с самыми широкими массами своими открытиями и научными разработками в области психодиагностики. Тест, который я хочу предложить вам сегодня разработан специалистами, специализирующимися на новом и крайне модном сейчас направлении в психологии психогеометрии. Разумеется, читателю предлагается упрощенный его вариант, потому что, на самом деле, тест этот очень серьезный и трудоемкий при обработке результатов, требует психологической подготовки. Но и этот, упрощенный, вариант, по-моему, крайне интересен. Во всяком случае, у вас есть возможность проверить. Нарисуйте на четырех небольших листках бумаги четыре фигуры (рисовать лучше фломастером или карандашом одного цвета): круг, треугольник, зигзаг и квадрат. Следите, чтобы фигуры были одинакового размера и прорисованы линиями одной толщины. Теперь перемешайте рисунки и предложите тому, чей характер хотите узнать поближе, разложить эти геометрические фигуры в порядке предпочтения. То есть надо выложить листки с рисунками в одну линию: на первое место положить ту фигуру, которая почему-то вызывает большую симпатию по сравнению с другими, на второе место ту, которая тоже нравиться, но поменьше, и так далее. На последнее место, таким образом, попадает фигура, которая нравиться меньше всего. И совершенно не важно: почему именно, важно только то, какая фигура оказалась на первом месте. Ну а теперь займемся диагностикой. Если на первом месте стоит квадрат, то перед вами прежде всего неутомимый труженик. Трудолюбие, усердие, почти маниакальная потребность доводить любое начатое дело до конца, упорство, позволяющее добиваться завершения работы вот, чем прежде всего знамениты истинные Квадраты. Выносливость, терпение и методичность обычно делают Квадрата высококлассным специалистом в своей области. Добавьте к этому постоянную потребность к получению новой информации. Причем, все поступающие сведения тут же систематизируются и раскладываются по полочкам. Квадраты заслуженно слывут эрудитами, по крайней мере в своей области. Вообще мыслительный анализ сильная сторона Квадрата. Они чрезвычайно внимательны к деталям, подробностям, что иногда все же мешает им видеть картину в целом. А самое главное: Квадраты самые настоящие педанты. Им очень важно, чтобы все лежало на своих привычных местах, а события проистекали по раз и навсегда установленному сценарию. Любое отступление от этого сценария способно надолго выбить Квадрата из колеи, заставить его растеряться, сделать беспомощным. Аккуратность, порядок соблюдения правил приличия могут развиться до парализующей крайности. И когда приходит время принимать решение, особенно связанное с риском, с возможностью потери статуса, Квадраты вольно или невольно затягивают его принятие. Кроме того рациональность, эмоциональная сухость и холодность мешают квадратам быстро устанавливать контакты с разными лицами. Этот человек вряд ли будет подолгу восхищаться прелестной формой цветка или красивой мелодией: эстетическая сторона этой жизни не его конек. И даже если вам показалось, что лицо Квадрата приняло в этот момент мечтательное, неземное выражение, то, будьте уверены, что в его голове в этот момент просто прокручивается рабочий план на завтрашний день во всех деталях. На первое место ваш визави поставил фигуру треугольника? Эта форма символизирует лидерство. И многие Треугольники ощущают в этом свое предназначение. Самая характерная особенность истинного Треугольника способность концентрироваться на главной цели. Треугольники энергичные, неудержимые, сильные личности, которые ставят ясные цели и, как правило, достигают их. Треугольник это очень уверенный в себе человек, который привык быть правым во всем. Сильная потребность управлять положением дел и быть первым, решать не только за себя, но и по возможности, за других, делают Треугольник личностью, постоянно соперничающей, конкурирующей с другими. Доминирующая установка в любом деле это установка на победу, выигрыш, успех. Он часто рискует, бывает нетерпелив и нетерпим к тем, кто колеблется в принятии решения или не готов следовать за нам. Для Треугольника очень травматично оказаться неправым в чем-то, признать свои ошибки, тем более публично. Если делом чести для Квадрата является достижение высшего качества выполняемой работы, то Треугольник стремиться достичь высокого положения, приобрести высокий статус или, иначе говоря, сделать карьеру. Главное отрицательное качество Треугольников сильный эгоцентризм, направленность на себя. Они заставляют все и всех вращаться вокруг себя, без них жизнь потеряла бы свою остроту. Треугольники на пути к вершинам власти не проявляют особой щепетильности в отношении моральных норм и могут идти к своей цели по головам других. Но это, впрочем, характерно для зарвавшихся Треугольников, которых никто вовремя не остановил. Круг это мифологический символ гармонии. Тот, кто уверенно выбирает его, искренне заинтересован прежде всего в хороших и теплых межличностных отношениях Высшая ценность для круга люди и их благополучие. Круг чаще всего служит тем клеем , который скрепляет и рабочий коллектив и семью, то есть приносит гармонию, тепло, любовь. Это про таких людей, наверное, говорят солнышко взошло . Они обладают высокой чувствительностью, способностью сопереживать, сочувствовать, эмоционально отзываться на переживания другого человека. Естественно, что люди тянуться к Кругам. Круги великолепно читают людей и в одну минуту способны распознать притворщика, обманщика. Они пытаются сохранить мир и ради этого иногда избегают занимать твердую позицию и принимать решения, не поддержанные большинством. Для круга нет ничего более тяжелого, чем вступать в межличностный конфликт. Он счастлив, когда люди ладят друг с другом, поэтому, когда у Круга возникает с кем-то конфликт, наиболее вероятно, что именно он уступит первым. Круги не отличаются решительностью, слабы во всякого рода интригах и часто не могут подать себя должным образом приукрасив. Все это ведет к тому, что над Кругами часто берут верх более сильные личности, например, Треугольники. Круги не слишком беспокоятся о том, в чьих руках будет находиться власть, лишь бы все были довольны и царил мир. Однако, в одном Круги проявляют завидную твердость: это касается нарушений вопросов морали или справедливости. Главная черта их стиля мышления ориентация на субъективный, человеческий фактор любой проблемы и стремление найти общее даже в противоположных точках зрения. Все это и умение чувствовать людей в малейших нюансах делает Кругов прирожденными психологами. Зигзаг символизирует креативность и творчество. Доминирующим стилем мышления Зигзага является синтетический стиль: комбинирование абсолютно различных, несходных идей, создание на этой основе чего-то нового и оригинального. Это стихия Зигзагов. Кстати, как показывает опыт тестирования, фигуру зигзага выбирает примерно один человек из пятидесяти. В отличие от Кругов Зигзаги вовсе не заинтересованы в консенсусе и добиваются договоренности не путем уступок, а заострением конфликта идей и построением новой концепции, в которой этот конфликт получает свое разрешение, то есть снимается. Используя свое природное остроумие, они могут быть весьма язвительными, открывая глаза другим на возможность нового решения. Зигзаги просто не могут трудиться в хорошо структурированных и контролируемых ситуациях. Их раздражают четкая иерархия и инструкции, строго фиксированные обязанности и способы работы. Им необходимо иметь большое разнообразие и высокий уровень стимуляции (одобрения окружающих) на рабочем месте. Если вы хотите получить от работы Зигзага максимальную прибыль, то дайте ему максимум независимости на рабочем месте и он удивит вас, оживет и начнет выполнять свое основное назначение генерировать новые идеи и методы работы. Зигзаги стремлены в будущее и больше интересуются возможностью, чем действительностью. Мир идей для них так же реален, как для остальных мир вещей. Зигзаги неутомимые проповедники своих идей и способны мотивировать всех вокруг себя. Однако, им не хватает дипломатии: они несдержаны, очень экспрессивны, что наряду с их эксцентричностью часто мешает им проводить свои идеи в жизнь. К тому же Зигзаги не сильны в проработке конкретных деталей (им это скучно) и не слишком настойчивы в доведении дела до конца, так как с утратой новизны теряется и интерес к идее. На первый взгляд это тестирование выглядит очень просто и доступно каждому. Но в этом-то его уникальность: при кажущейся простоте точность получаемой психологической характеристики личности поразительна! Кроме того, можно выявить не только самые важные черты человека, но и те, что у него находятся в меньшинстве для этого достаточно посмотреть, какую фигуру испытуемый поставил на последнее место.

 Пирамида и здоровье

Одним из уникальных лечебных средств является четырехгранная пирамида, по форме напоминающая пирамиды Хеопса, Хефрена и других фараонов, расположенные на плато Гиза в Египте.

Своей (пока не объясненной до конца наукой) энергией она достаточно активно стимулирует жизненные силы больного организма, а тот, в свою очередь, уже легче справляется с недугом.

С помощью такой пирамиды достаточно быстро улучшается состав крови, нормализуется давление, стихают боли, ускоренно заживают переломы костей, раны, а также повреждения, связанные с операциями, радиотерапией и опухолями. Исцеляет пирамида и инфекционные (микробно-паразитарные) заболевания.

Иными словами, терапия с помощью пирамиды – уникальное средство при многих заболеваниях, и даже, если человек, будучи в полном здравии, иногда принимает (в малых дозах) воду или съедает небольшие порции пищи, выдержанные в пирамиде, или отдыхает иногда в большой или над малыми пирамидами, то шансы заболеть у него минимальны.

  Изготовление пирамид.

Изготавливается домашняя пирамида из природного материала (доски, картона, оргстекла, плоского шифера, фанеры и т.п.), обладающего диэлектрическими (изоляционными) свойствами, без единого гвоздя и без применения прочих металлов, которые своим полем вносят искажения в поле пирамидального пространства.

Энергия этого пространства должна быть чистой, без всяких искажений, тогда целебные свойства пирамиды будут максимальны.

Пирамида – это многогранник, основанием которого служит многоугольник, а боковыми гранями являются треугольники, имеющие общую величину.

В основании правильной пирамиды всегда лежит правильный многоугольник (например, для четырехгранной пирамиды – квадрат), а боковые грани – равнобедренные треугольники, равные между собой. Высота пирамиды равна длине перпендикуляра, опущенного из вершины в центр основания (центром правильного многоугольника, лежащего в основании пирамиды служит точка пересечения его диагоналей).

Кроме высоты характеристиками пирамиды служат длина основания и высота боковой грани (апофема) пирамиды.

Домашняя пирамида может иметь любые размеры, но соотношение ее высоты и длины основания должно быть строго определенным, а именно: длина основания должна превышать высоту пирамиды в 1,6 раза. Такое соотношение соответствует пропорции золотого сечения, или гармоничного деления.

Таким образом, умножив заданную высоту пирамиды на 1,6 мы получим длину ее основания. Для определения высоты боковой грани (апофемы пирамиды) необходимо заданную высоту пирамиды умножить на 1,35.

Следует помнить, что с удвоением высоты пирамиды активность ее действия возрастает во много (50-100 и более) раз. Следовательно, если позволяет возможность, устанавливайте пирамиды с максимальной высотой.

Одно из ребер пирамиды должно быть сориентировано с помощью компаса строго на север.

Если она построена в благоприятном месте – на возвышенности, без металла, далеко от железобетонных домов и конструкций, вдали от линий электропередач, насыпей и железных дорог, с помощью компаса правильно ориентирована по сторонам света, такая пирамида работает сразу и очень эффективно!

В домах, квартирах пирамидки следует ставить подальше от металлических предметов и конструкций, которые нарушают естественное магнитное поле Земли и тем самым снижают целебные свойства пирамиды. К таким предметам относятся батареи отопления, водопровод, канализация и т.п. Если дома сделаны из железобетонных конструкций, пирамидки в них могут быть не столь эффективными. В таком случае пирамиду лучше построить на своем дачном участке и с ее помощью восстанавливать здоровье.

Следует помнить, что любая пирамида должна изготавливаться психически уравновешенным человеком, у которого во время изготовления должны быть добрые и светлые помыслы, и выполнять эту работу строитель должен с душой.

Если пирамидки построены кое-как, с нарушением пропорций золотого сечения, не сориентированы по сторонам света по компасу, можно предположить, что пользы они не принесут, а возможно, даже и вред.

 

 

 

 

 

 

Размеры домашней пирамиды

 

Высота	Длина основания	Апофема	Длина ребра
10 см	10х1,6 = 16 см	10х1,35 = 13,5 см	15,70 см
15 см	15х1,6 = 24 см	15х1,35 = 20,25 см	25,53 см
20 см	20х1,6 = 32 см	20х1,35 = 27 см	31,38 см
30 см	30х1,6 = 48 см	30х1,35 = 40,5 см	47,07 см
40 см	40х1,6 = 64 см	40х1,35 = 54 см	62,76 см
50 см	50х1,6 = 80 см	50х1,35 = 67,5 см	78,46 см
100 см	100х1,6 = 160 см	100х1,35 = 135 см	156,92 см
250 см	250х1,6 = 400 см	250х1,35 = 337,5 см	392,30 см
300 см	300х1,6 = 480 см	300х1,35 = 405 см	470,77 см
500 см	500х1,6 = 800 см	500х1,35 = 675 см	784,61 см
1000 см	1000х1,6 = 1600 см	10х1,35 = 1350 см	1569,24 см

      Следует помнить, что максимальными энергетическими возможностями всех правильно изготовленных и установленных пирамид (больших и малых) обладает их внутреннее пространство на уровне от 1/3 до 2/3 высоты пирамиды. Все остальное пространство пирамид энергетически минимально, соответственно, и отдача минимальна.

В верхней части пирамиды желательно сделать небольшой надрез, чтобы образовалось отверстие (для пирамиды с основанием 4 м диаметр отверстия составляет 60-70 мм) – волновод, которое нужно пирамиде для выхода в окружающее пространство избытка энергии, которая образуется внутри в процессе работы. В основании по центру также делается отверстие (для пирамиды с основанием 4 м диаметр отверстия составляет 10 мм). С помощью циркуля рисуют три концентрические окружности вокруг центра основания, по которым распределяют равномерно около 30 аналогичных отверстий (для пирамиды с основанием 4 м диаметры окружностей составляют 100 см, 250 см и 400 см). Отверстия в основании нужны для беспрепятственного получения энергии Земли. На высоте 1/3 , 1 / 2 и 2/3 пирамиды устанавливаются полочки.

Рабочие зоны пирамиды

 

 

 

 

 

 

 

Рис. 2. Рабочие зоны пирамиды

На высоте 2/3 пирамиды на полочках размещают жидкости, воду, настойки трав для зарядки целебными энергиями пирамиды.

На высоте 1 /2 заряжают алюминиевую фольгу, металлы.

На высоте 1/3 размещают продукты, зерно, семена перед посадкой, затачивают лезвия.

Для малых пирамид загрузка внутреннего объема должна составлять не больше 8-10% от объема. Такой заряд будет оптимальным.

 

Примеры использования пирамид.

При тяжелых и множественных заболеваниях больному следует пользоваться большими пирамидами для отдыха – возможности исцеления в них практически не ограничены. Время пребывания в больших пирамидах сугубо индивидуально, для особо чувствительных пациентов – не более 15 минут. При переутомлении достаточно 30 минут пребывания в пирамиде для восстановления сил и избавления от дискомфорта.

Можно использовать и комнатные пирамидки. Больной отдыхает на кровати без металла, под которой вдоль его тела установлены до пяти (10-15 см высотой) пирамидок.

Для исцеления организма пустые пирамидки хороши, но в сочетании с приемом пирамидальной воды или травяных настоев, выдержанных в течение 24 часов внутри пирамиды на уровне 2/3 высоты (в верхней части). Даже малая толика такой воды приносит больному пользу. Пирамидный настой делается примерно так: в емкость (стакан или банку) кладут указанное в рекомендации лекарственное сырье, заливают нужным количеством кипятка, закрывают капроновой крышкой и настаивают нужное время на подставке на уровне 2/3 высоты пирамиды. Вода может храниться в пирамиде длительное время.

При всех внутренних болях, при болях в мышцах и суставах наружно в виде компресса можно использовать алюминиевую фольгу, которую перед этим заряжают в пирамиде 24 час на уровне 1 /2 высоты, используя диэлектрическую подставку. Заряженную таким образом фольгу обворачивают слоем льняного полотна и прикладывают на больное место или сустав. Сверху этот компресс закрывают, закрепив льняным полотном или бинтом и оставляют на всю ночь. Такие компрессы ставят и при болях головы, живота, груди, конечностей. С помощью таких компрессов боли, как правило, проходят достаточно быстро – проходят совсем!

Кроме целительных свойств, пирамиды полезны и для многих других целей.

Можно выдерживать семена перед посадкой в пирамиде в течение 10-15 дней на уровне 1/3 высоты, при этом повышается всхожесть и урожайность примерно в 2 раза.

Пирамиды благоприятно влияют на животных. Можно построить большую пирамиду рядом с местом их пребывания, можно расположить несколько малых пирамид. Аквариум можно залить пирамидальной водой, можно накрыть пирамидой, ориентированной по сторонам света на 24 и более часа.

В пирамидах, особенно больших, можно хранить на полках на 1/3 высоты долгое время скоропортящиеся продукты питания без риска, что они испортятся. При этом даже улучшаются их вкусовые качества.

В малых пирамидках на подставе в 1/3 высоты кладут затупленные лезвия и ножи на 24 часа для заточки.

Если в большой пирамиде на высоте от 1/3 до 1/ 2 поставить самодельный генератор, то пирамида будет способна вырабатывать электрическую энергию. Генератор делается из листов алюминия, меди или фольгированного пластика. Собранный генератор нужно подключить к аккумулятору, желательно щелочному, запараллелив его и с нагрузкой. При изготовлении такого генератора следует иметь в виду, что чем больше в нем будет пластин, тем большее напряжение он сможет дать, и чем больше будет поверхность пластин, тем больший ток сможет вырабатывать генератор.

 

Рис 3.  Примерный вид генератора в горизонтальном (нерабочем) положении.

Рабочее положение – вертикальное.

1 – токосъемные металлические пластины;

2 – изоляционные планки (с помощью клея удерживают пластины);

3 – аккумулятор;

4 – нагрузка (лампа).

 

Размещение генератора в пирамиде. 

В засушливых районах можно сделать конденсатор (накопитель) воды и сбора ее из воздуха, размещая пирамиду на фундаменте с уклоном к центру пирамиды с отверстием трубы в центре основания. Труба выводится под уклоном для самостоятельного стока воды за пределы фундамента. Сверху бетонированную площадку засыпают горкой гравием на возможно большую высоту. Насыпь укрепляют с помощью пирамидального каркаса (можно металлического), обтянутого сеткой (желательно оцинкованной). Такое крепление не мешает свободному притоку и оттоку воздуха. Пирамида высотой 250 см способна наполнить водой емкость 100-200 л за сутки.