I вариант
1. Решите уравнение √4-6х-х2 =х+4
2. Решите неравенство log2 (х-1) +log2 х ≤ 1
3. Решите уравнение 2х 5х=0,1 103х-1
4. Решите уравнение cos x – sin (π/2-x) + sin (π-x)=0
2
5.Вычислите ∫(4х2+х-1)dx
1
6. Развёртка боковой поверхности цилиндра является квадратом диагональ, которого равна 10 см. Найдите площадь боковой поверхности.
7. Радиус основания конуса равен 6 см, а высота – 4 см. Найдите объём конуса.
8.В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 300. Сторона основания пирамиды равна 12 см. Найдите площадь поверхности пирамиды.
9. Найдите наибольшее и наименьшее значение функции 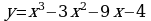 на отрезке [-4; 4]
на отрезке [-4; 4]
10. Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по законуS=0,5t2 +3t +2 (м), где t – время движения в секундах. Через какое время после начала движения скорость тела окажется равной 15 м/с?
II вариант
1.Решите уравнение √6-4х-х2 =х+4
2. Решите неравенство log2 (х-1) +log2 х ≤ 1
3. Решите уравнение 2х+1 5х+1=0,001(10х-2)3
4.Решите уравнение 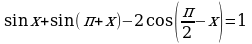
3
5. Вычислите ∫(x2-2х+3)dx
-3
6. Радиус основания конуса равен 5 см, а образующая конуса равна 13 см. Найдите объём конуса.
7.Площадь осевого сечения цилиндра равна 20 см2. Найдите площадь его боковой поверхности.
8. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 600.Высота пирамиды равна 6 см. Найдите площадь боковой поверхности пирамиды.
9.Найдите наибольшее и наименьшее значения функции 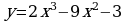 на отрезке [-1 ;4]
на отрезке [-1 ;4]
10. Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по закону S =0,5t2 - 3t +8 (м), где t – время движения в секундах. Через какое время после начала движения скорость тела окажется равной 15 м/с?
III вариант
1.Вычислите 251,5+(0,25)-0,5-810.75.
2.Решите неравенство log½(х2+7х+10)˃-2
3.Решите уравнение 7х+2-14 7х=5
4.Решите уравнение 2sin 2 х+7cosх+2=0
5.Найдите точки экстремума функции f(х)=3х4 -4х3 +2.
6.Объем конуса с радиусом основания 6 см равен 96π см3 . Найдите площадь боковой поверхности конуса.
7.Два металлических куба с ребрами 1 см и 2 см соответственно сплавлены в один куб. Определите ребро этого куба.
8.В правильной четырехугольной пирамиде высота равна 12 см, а апофема-15 см. Найдите боковое ребро пирамиды.
9. Найдите площадь фигуры, ограниченной графиком функции
f(х)=х2- 6х+10, прямыми х= -1, х=3 и осью абсцисс.
10. Билет на автобус стоит 30 рублей. Определите, на сколько поездок хватит 100 рублей, если стоимость билета снизят на 10%.
IV вариант.
1.Вычислите 91,5-810,5-(0,5)-2
2.Решите неравенство log2(х2-13х+30)‹ 3
3.Решите уравнение 10 5х-1+5х+1=7
4.Решите уравнение 5-4sin2x=4cosx
5.Найдите точки экстремума функции f(х)=2х3 -3х2 -1
6.Высота конуса равна 8см, объем 24π см3. Найдите площадь полной поверхности конуса.
7.Три одинаковых металлических куба с ребрами по 4 см сплавлены в один куб. Определите ребро этого куба.
8. Высота правильной треугольной пирамиды равна 8см, а боковое ребро-10 см. Найдите площадь боковой поверхности пирамиды.
9.Найдите площадь фигуры, ограниченной графиком функции f(х)=х2+5х+6, прямыми х= -1, х=2 и осью абсцисс.
10.Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в спортивном зале площадью 6х12м2 , если на 1м2 расходуется 300 граммов краски.







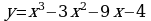 на отрезке [-4; 4]
на отрезке [-4; 4]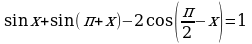
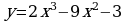 на отрезке [-1 ;4]
на отрезке [-1 ;4]









