Элементы комбинаторики и теории вероятности. 9 класс

Комбинаторные задачи – задачи, для решения которых приходится составлять различные комбинации из конечного числа элементов и подсчитывать их количество.

Комбинаторика – раздел математики, рассматривающий такие задачи.

«Комбинаторика» - от латинского combinare (соединять, сочетать).

На практике часто приходится делать перебор определённого количества данных. Например, учителю приходится распределять различные виды работ между группами учащихся, офицеру выбирать из солдат наряд, агроному размещать культуры на полях, завучу составлять расписание и т.д. В данном случае речь идёт о всевозможных комбинациях объектов. Задачи такого типа называются комбинаторными задачами. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой. Как самостоятельный раздел математики комбинаторика оформилась в Европе в XVIII веке. Некоторые комбинаторные задачи решали в Индии во II веке до н. э., в Древнем Китае, позднее в Римской империи.

Термин «комбинаторика» был введен в математический обиход знаменитым Лейбницем.

Готфрид Вильгельм Лейбниц (1.07.1646 – 14.11.1716) – всемирно известный немецкий ученый, занимался философией, математикой, физикой, организовал Берлинскую академию наук и стал её первым президентом.

В 1666 году Лейбниц опубликовал "Рассуждения о комбинаторном искусстве". В своём сочинении Лейбниц ввел специальные символы, термины для подмножеств и операций над ними. В течение всей своей жизни Лейбниц многократно возвращался к идеям комбинаторного искусства. В XVIII веке к решению комбинаторных задач обращались выдающиеся математики.

В XVIII веке к решению комбинаторных задач обращались выдающиеся математики.

Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических и латинских квадратов.

Л. Эйлер

В 1713 году было опубликовано сочинение Я. Бернулли "Искусство предположений", в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. Сочинение состояло из 4 частей, комбинаторике была посвящена вторая часть, в которой содержатся формулы. Для вывода формул автор использовал наиболее простые и наглядные методы, сопровождая их многочисленными таблицами и примерами. В работах Я. Бернулли и Лейбница тщательно изучены свойства сочетаний, размещений, перестановок.

Я. Бернулли

Способ перебора возможных вариантов

Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев, Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?

Решение:

АГ, АС, АФ,

ГС, ГФ,

СФ.

Ответ: существует 6 вариантов выбора пары.

Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи числа каждую из них не более одного раза.

Решение:

1 , 1 , 1 , 1 , 1 , 1 ,

3 , 3 , 3 , 3 , 3 , 3 ,

5 , 5 , 5 , 5 , 5 , 5 ,

713 , 715 , 731 , 735 , 751 , 753 .

3

3

5

7

5

73

75

7

3

5

71

75

7

57

51

5

1

1

37

71

73

13

17

31

Ответ: Из цифр 1, 3, 5, 7 можно составить 24 трехзначных

числа

Дерево возможных вариантов

Первая цифра

4

1 3 5 7

Вторая цифра

3

1 5 7 1 3 7 1 3 5

3 5 7

Третья цифра

2

5 7 1 7 1 5 3 7 1 7 1 3 3 5 1 5 1 3

5 7

3 7 3 5

Общее число вариантов – 4 · 3 · 2 = 24

Комбинаторное правило умножения

Пусть имеется n элементов и требуется выбрать из них некоторые k элементов.

Если 1-ый элемент можно выбрать n 1 способами,

2-ой элемент можно выбрать n 2 способами,

3-ий элемент можно выбрать n 3 способами,

………………………………………………… .,

k -ый элемент можно выбрать n k способами ,

то все k элементов могут быть выбраны

n 1 · n 2 · n 3 · … · n k способами.

Из города А в город В ведут две дороги, из города В в город С - три дороги, из города С до пристани – две дороги. Сколькими способами туристы могут проехать из города А через города В и С до пристани ?

А

Пристань

В

С

Путь из А в В туристы могут выбрать - 2 способами.

Из А в С существует 2 · 3 = 6 маршрутов.

Из А к Пристани существует 2 · 3 · 2 = 12 способов выбора маршрута.

В кафе предлагают два первых блюда: борщ, рассольник – и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель.

Первое блюдо

Б

Р

Ответ: 2 · 4 = 12 обедов

Второе блюдо

С

Г

П

С

К

Г

П

К

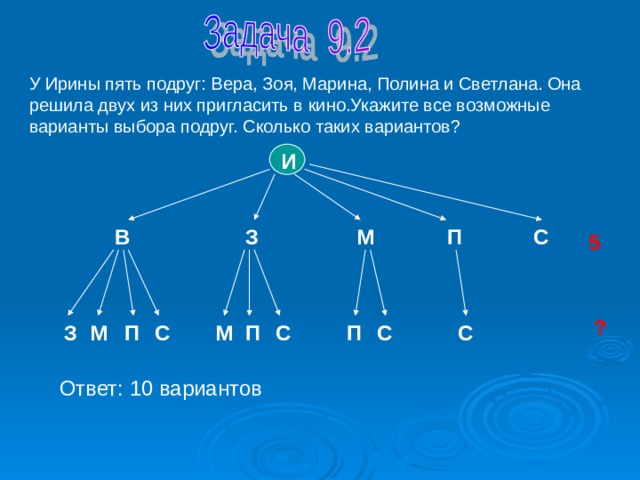
У Ирины пять подруг: Вера, Зоя, Марина, Полина и Светлана. Она решила двух из них пригласить в кино.Укажите все возможные варианты выбора подруг. Сколько таких вариантов?

И

М

С

П

В

З

5

?

С

С

П

П

С

С

П

М

З

М

Ответ: 10 вариантов

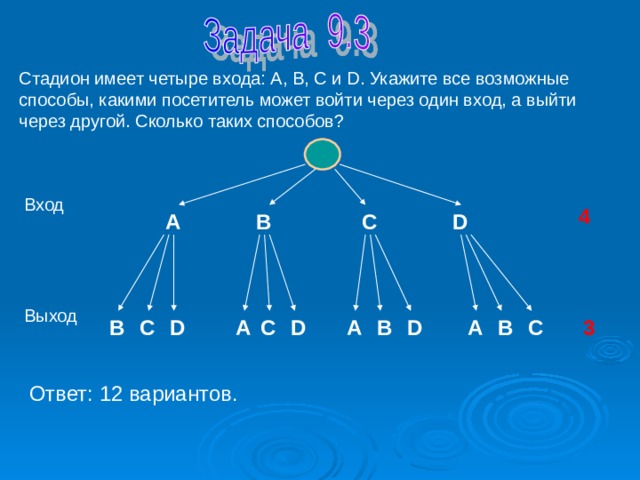
Стадион имеет четыре входа: А, В, С и D . Укажите все возможные способы, какими посетитель может войти через один вход, а выйти через другой. Сколько таких способов?

Вход

4

D

С

В

А

Выход

3

С

С

В

А

D

В

А

D

А

D

С

В

Ответ: 12 вариантов.

Укажите все способы, какими можно разложить три яблока в две вазы.

В

В

В1

В2

3

0

3

0

2

1

1

2

2

1

Ответ: 2 способа

0

3

Ответ: 4 способа

В1

В2

В

В

---

К, Ж ,З

Ж, З

К

Ж

К, З

З

К, Ж

Ответ: 4 способа

Ответ: 8 способов

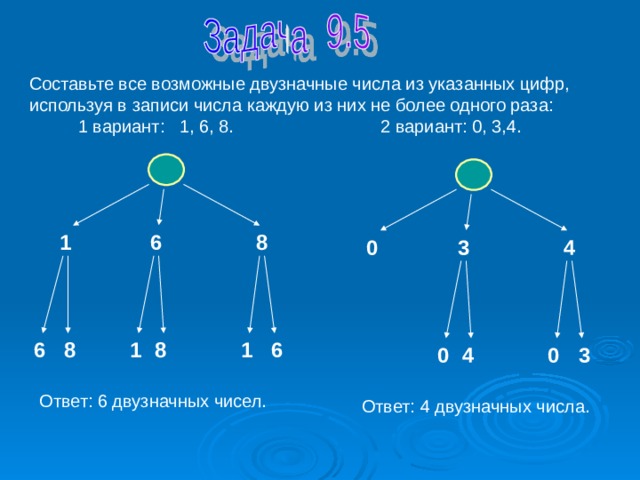
Составьте все возможные двузначные числа из указанных цифр, используя в записи числа каждую из них не более одного раза: 1 вариант: 1, 6, 8. 2 вариант: 0, 3,4.

1

6

8

0

3

4

6

6

1

8

1

8

0

4

0

3

Ответ: 6 двузначных чисел.

Ответ: 4 двузначных числа.

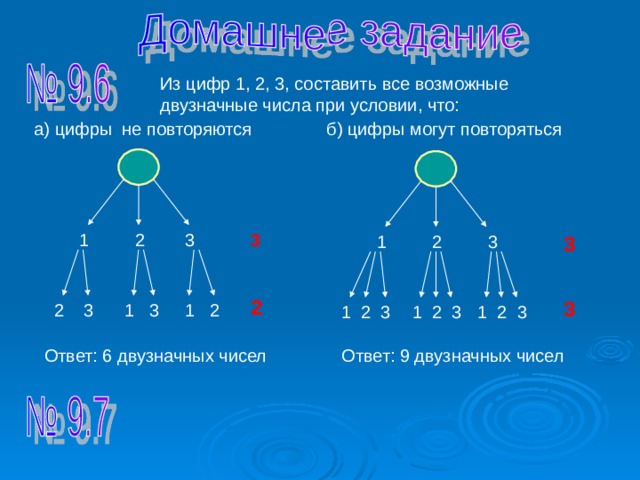
Из цифр 1, 2, 3, составить все возможные двузначные числа при условии, что:

б) цифры могут повторяться

а) цифры не повторяются

1

2

3

3

2

3

1

3

2

3

1 2

2 3

1 3

1 2 3

1 2 3

1 2 3

Ответ: 6 двузначных чисел

Ответ: 9 двузначных чисел

Используя цифры 0, 2, 4, 6, составить все возможные трехзначные числа, в которых цифры не повторяются.

3

2

4

6

3

0 2 6

0 2 4

0 4 6

2

0 4

4 6

0 6

0 4

2 6

0 6

0 2

2 4

0 2

Ответ: 18 трехзначных чисел

В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии. Сколько всего партий было сыграно?

1 2 3 4 5 6 7 8 9

1

2

3

4

5

6

7

8

9

В шахматном турнире участвуют 9 человек. Каждый из них сыграл с каждым по одной партии. Сколько всего партий было сыграно?

1 2 3 4 5 6 7 8 9

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

▓

1

2

3

4

5

Ответ: 36 партий

6

7

8

9

В соревнованиях по футболу участвовало 12 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле соперника. Сколько всего игр было сыграно? Решение:

1 команда сыграла - (12 – 1) · 2 = 22 игры,

2 команда сыграла - (12 - 2) · 2 = 20 игр,

3 команда - (12 - 3) · 2 = 18 игр,

4 команда - (12 - 4) · 2 = 16 игр,

5 команда - (12 - 5) · 2 = 14 игр,

………………………………………………… ..

10 команда - (12 - 10) · 2 = 4 игры,

11 команда - (12 - 11) · 2 = 2 игры.

Было сыграно - 22 + 20 + 18 + 16 + 14 + 12 + 10 + 8 + 6 + 4 + 2 = 132 игры.

При встрече 8 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Решение:

1-ый человек - обменялся рукопожатиями с 7, 2-ой - с 6, 3-ий - с 5, 4-ый - с 4, 5-ый - с 3, 6-ой - с 2, 7-ой - с 1, 8-ой - ?

Всего было сделано – 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 рукопожатий.

На входной двери дома установлен домофон, на котором установлены цифры 0, 1, 2, …, 8, 9. Каждая квартира получает кодовый замок из двух цифр типа 0 – 2, 3 – 7, 7 – 3, 8 – 8 и т. п., позволяющий открывать входную дверь. Хватит ли кодовых замков для всех квартир дома, если их 96. Решение:

Код составлен из двух цифр.

Для 1 - ой цифры кода существует 10 вариантов.

Для 2 – ой цифры кода - 10 вариантов.

Всего существует 10 · 10 = 100 вариантов кодового замка, а квартир 96.

Ответ: кодовых замков хватит для всех квартир.

Из села Дятлова в село Матвеевское ведут три дороги, а из села Матвеевское в село Першино – четыре дороги. Сколькими способами можно попасть из Дятлова в Першино через Матвеевское?

Решение:

Д

П

М

Попасть из Дятлова в Матвеевское можно - 3 способами,

попасть из Матвеевского в Першино можно - 4 способами,

попасть из Дятлова в Першино можно – 3 · 4 = 12 способами.

Ответ: 12 способов.

Петр решил пойти на новогодний карнавал в костюме мушкетера. В ателье проката ему предложили: пять видов брюк, шесть камзолов, три шляпы, две пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?

Решение:

Для выбора брюк существует - 5 вариантов,

для выбора камзола - 6 вариантов,

для выбора шляпы - 3 варианта,

для выбора пары сапог - 2 варианта.

Можно составить 5 · 6 · 3 · 2 = 180 вариантов карнавального костюма.

1 вариант

2 вариант

В киоске продают 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт с маркой? Составьте дерево возможных вариантов.

У Светланы 3 юбки и 5 кофт удачно сочетающихся по цвету. Сколько различных комбинаций одежды имеется у Светланы? Составьте дерево возможных вариантов.

Учащиеся 9 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 24 учащихся?

Каждому из 24 учеников потребуется 23 своих фотографии. Всего необходимо 24 · 23 = 552 фотографии.

Решение:

В кафе имеются три первых блюда , пять вторых блюд и два третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?

Решение:

Первое блюдо можно выбрать – 3-мя способами, второе блюдо - 5-ю способами, третье блюдо - 2-мя способами, Обед из трех блюд можно выбрать 3 · 5 · 2= 30 способами.