ЭЛЕМЕНТЫ ТЕОРИИ ИГР
Предмет теории игр, основные понятия
Ранее рассматривались задачи принятия решений, в которых выбор оптимального решения осуществлялся одним лицом. В теории игр изучаются задачи принятия решений, в которых участвуют несколько лиц, принимающих решения, а оптимальное значение целевой функции для каждого из них зависит и от решений, принимаемых всеми остальными участниками.
Математическую дисциплину, исследующую ситуации, в которых принятие решения зависит от нескольких участников, называют теорией игр.
Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия. Типичными примерами подобных ситуаций могут служить планирование боевых операций противоборствующих армий, рекламирование конкурирующих товаров.
Возникновение этой теории относится к первой половине ХХ века, когда вышла в свет монография Неймана и Моргенштерна «Теория игр и экономического поведения». В дальнейшем она превратилась в самостоятельное математическое направление.
В теории игр лиц, принимающих решения, называют игроками, а целевую функцию - платёжной функцией или функцией выигрышей.
Фактически игра представляет собой совокупность правил, регламентирующих поведение сторон.
Ходом в теории игр называется выбор одного из предполагаемых правилами игры действий и его осуществление.
Ходы бывают личные и случайные. При личном ходе игрок сознательно выбирает и осуществляет тот или другой вариант действий (пример – любой ход в шахматах). При случайном ходе выбор осуществляется не волей игрока, а каким-то механизмом случайного выбора (бросание монеты, игральные кости, вынимание карты из колоды). Некоторые игры (так называемые «азартные») состоят только из случайных ходов – ими теория игр не занимается. Её цель – оптимизация поведения игрока в игре, где (может быть, наряду со случайными) есть личные ходы. Такие игры называются стратегическими.
Каждый из игроков характеризуется своим множеством возможных способов поведения или, как ещё говорят, своим множеством стратегий. Пусть 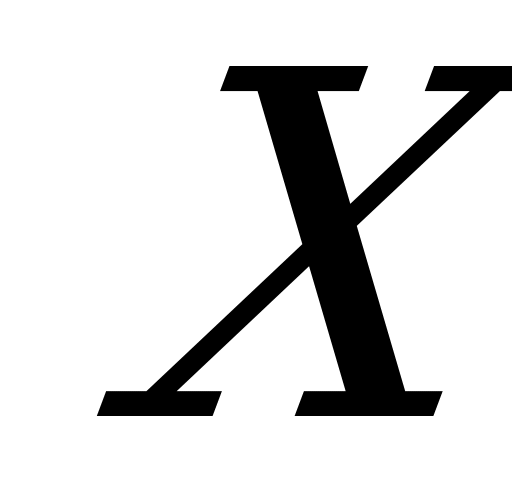 – множество стратегий первого игрока,
– множество стратегий первого игрока, 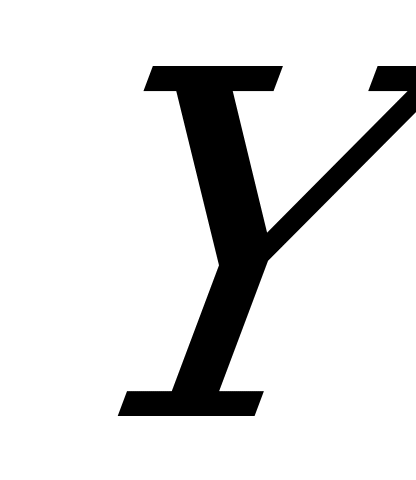 - множество стратегий второго игрока,
- множество стратегий второго игрока,  - множество стратегий третьего игрока и т.д. Игра состоит в том, что каждый из игроков независимо выбирает свой способ поведения, т.е. свою стратегию, что порождает определённую ситуацию, разрешающуюся соответствующими результатами для каждого из игроков. Предполагается, что интересы участников игры поддаются количественному описанию, т.е. результат игры (выигрыш) определяется некоторым числом.
- множество стратегий третьего игрока и т.д. Игра состоит в том, что каждый из игроков независимо выбирает свой способ поведения, т.е. свою стратегию, что порождает определённую ситуацию, разрешающуюся соответствующими результатами для каждого из игроков. Предполагается, что интересы участников игры поддаются количественному описанию, т.е. результат игры (выигрыш) определяется некоторым числом.
На формальном языке ситуация – это набор стратегий 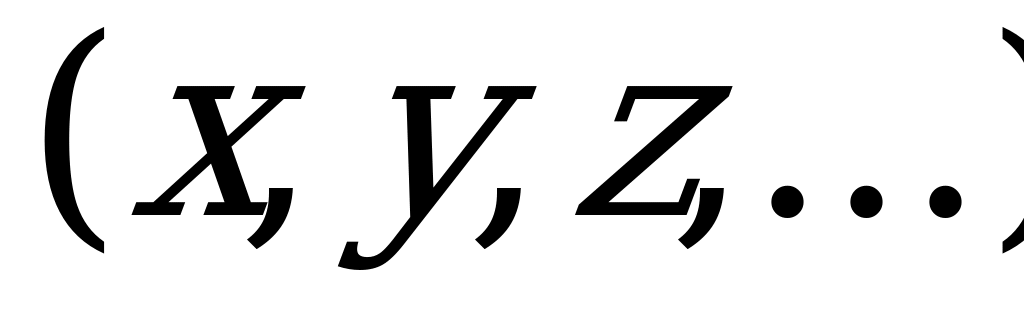 , где
, где  ,
,  ,
, 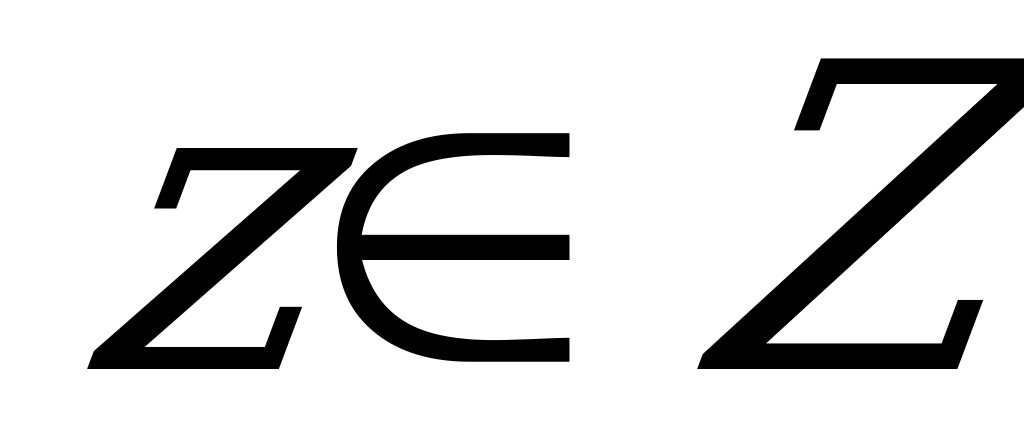 , …, и на множестве всех ситуаций заданы функции
, …, и на множестве всех ситуаций заданы функции 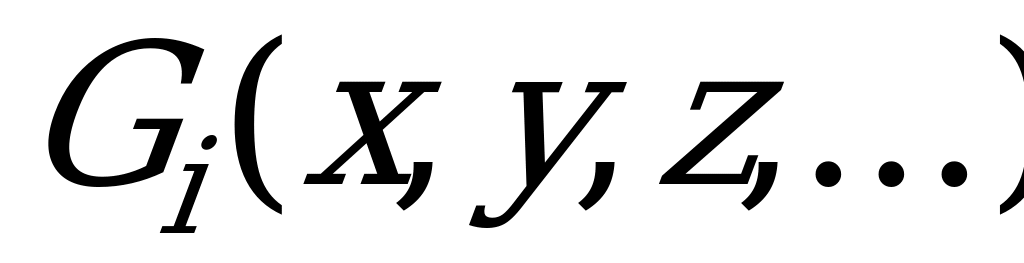 , указывающие значения результатов ситуации
, указывающие значения результатов ситуации 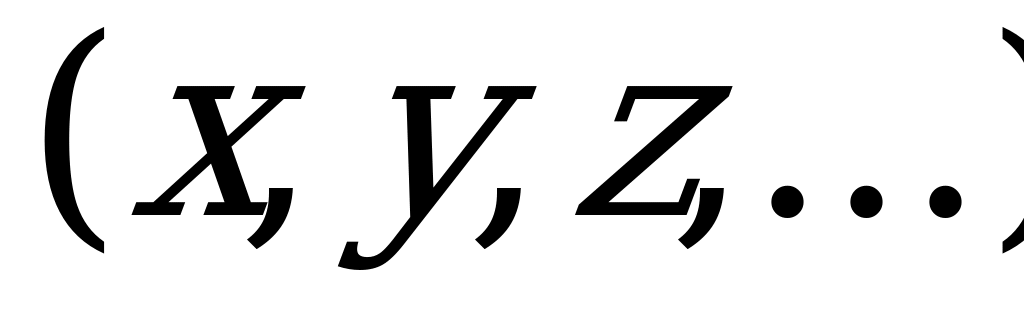 для каждого игрока. Предполагается, что каждый из игроков заинтересован в возможно большем значении «своей» функции. Функции
для каждого игрока. Предполагается, что каждый из игроков заинтересован в возможно большем значении «своей» функции. Функции 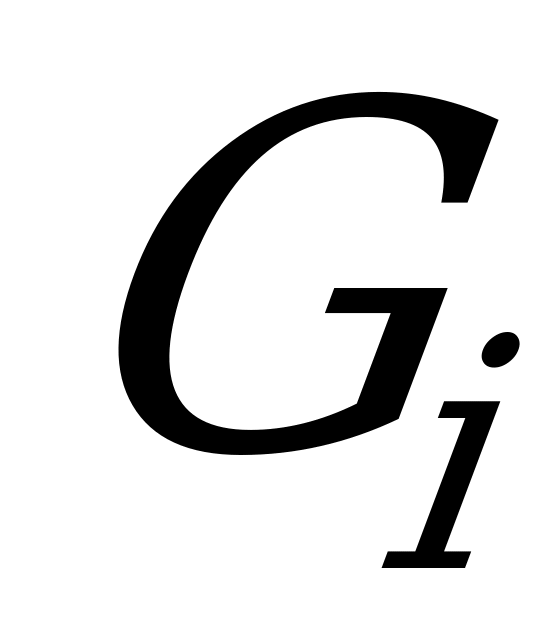 называют функциями выигрышей игроков.
называют функциями выигрышей игроков.
Таким образом, чтобы задать игру, нужно для каждого из игроков задать его множество стратегий и его функцию выигрыша. Для мотивированного принятия решения о выборе своей стратегии каждый из игроков должен анализировать мотивацию поведения других игроков, а значит, знать не только их множества стратегий, но и их функции выигрышей. Поэтому предполагается, что вся информация об игре (множества стратегий, функции выигрышей) известна всем игрокам.
Функции 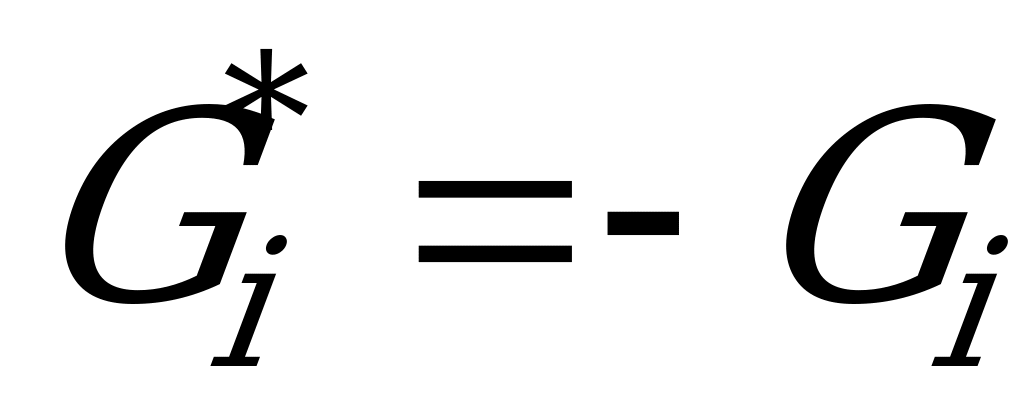 называют функциями проигрышей.
называют функциями проигрышей.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.
Классификацию игр проводят по различным признакам:
-
по числу игроков;
-
по числу стратегий;
-
по свойствам платёжной функции;
-
по характеру предварительной договорённости между игроками.
Игра, в которой участвуют два игрока, называется парной, а игра, в которой участвуют более двух игроков – множественной.
При наличии двух игроков могут возникать как конфликтные ситуации, так и необходимость в координированных действиях (кооперация). Если в игре участвует не менее трёх игроков, то могут создаваться коалиции, то есть группы из двух или более игроков, имеющих общую цель и координирующих свои стратегии.
По количеству стратегий различают игры конечные и бесконечные. Если хотя бы один из игроков располагает бесконечным множеством стратегий, то игру называют бесконечной. Если же каждый из игроков располагает конечным множеством стратегий, то игру называют конечной.
Важным классом игр являются так называемые игры с нулевой суммой. В игре с нулевой суммой общая сумма выигрышей всех игроков равна нулю (то есть, игрок выигрывает только за счёт других):  .
.
В игре с нулевой суммой и двумя участниками выигрыш одного из них равен проигрышу другого: 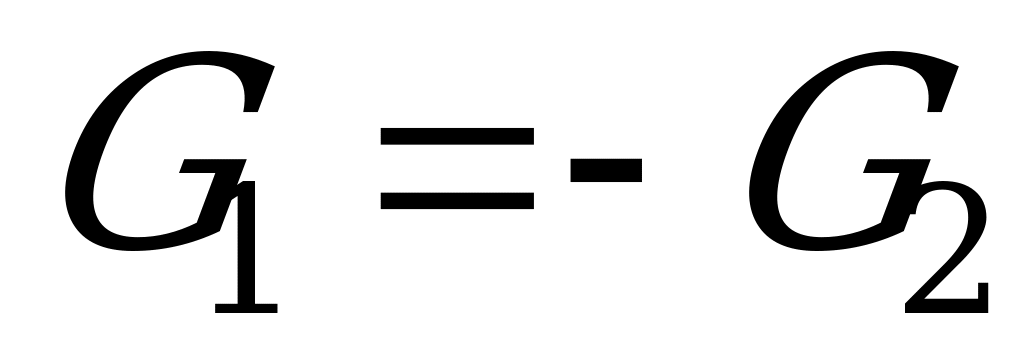 . В таких играх достаточно задавать лишь одну из функций, например, функцию выигрыша первого игрока. Таким образом, в играх двух лиц с нулевой суммой существует конфликт между игроками, и поэтому их называют также антагонистическими играми. В общем случае, в игре с нулевой суммой, как правило, имеют место и конфликты, и согласованные действия игроков.
. В таких играх достаточно задавать лишь одну из функций, например, функцию выигрыша первого игрока. Таким образом, в играх двух лиц с нулевой суммой существует конфликт между игроками, и поэтому их называют также антагонистическими играми. В общем случае, в игре с нулевой суммой, как правило, имеют место и конфликты, и согласованные действия игроков.
Пример игры с нулевой суммой. Первый игрок выбирает одну из двух сторон монеты. Второй игрок, не зная выбора первого, также выбирает одну из сторон. После того как оба игрока произвели свой выбор и монеты показаны, первый игрок выигрывает 10 ден.ед., а второй проигрывает 10 ден.ед., если они выбирают одинаковые стороны монет (оба говорят «Орёл» или «Решка»). Если они выбирают разные стороны монет, то второй игрок выигрывает 10 ден.ед., а первый – проигрывает 10 ден.ед..
Матрица  выигрышей первого игрока имеет следующий вид:
выигрышей первого игрока имеет следующий вид:
Стратегии 2-го игрока
Орёл Решка
Стратегии 1-го игрока 

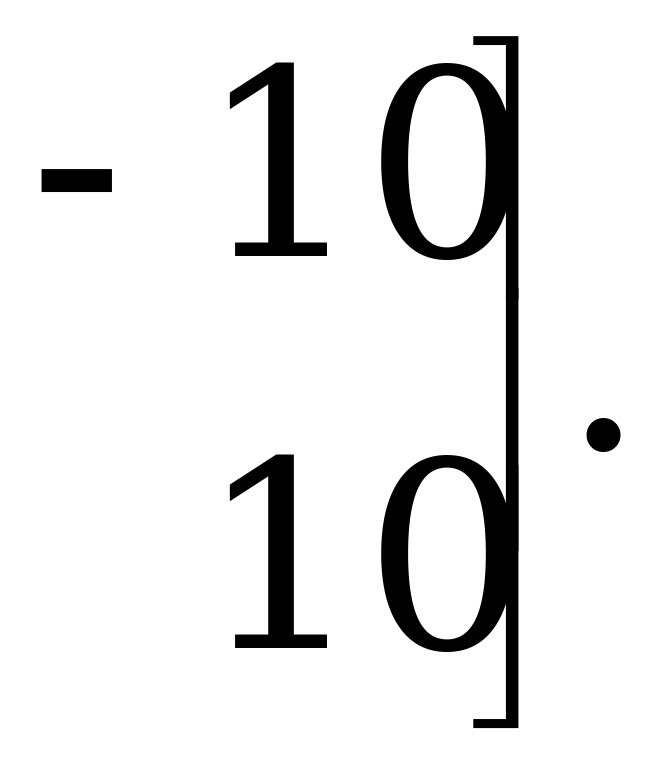
Соответственно, матрица выигрышей второго игрока 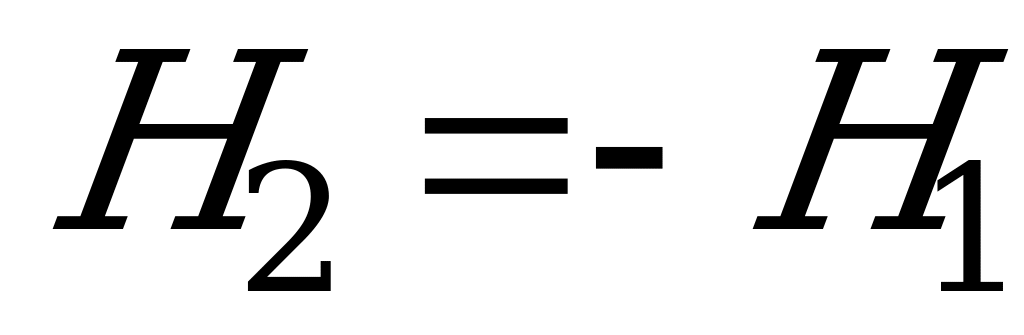 .
.
Для наглядности матрицы выигрышей обоих игроков объединяют в одну биматрицу, которая даёт полную информацию о всей игре:
Стратегии 2-го игрока
Орёл Решка
Стратегии 1-го игрока 
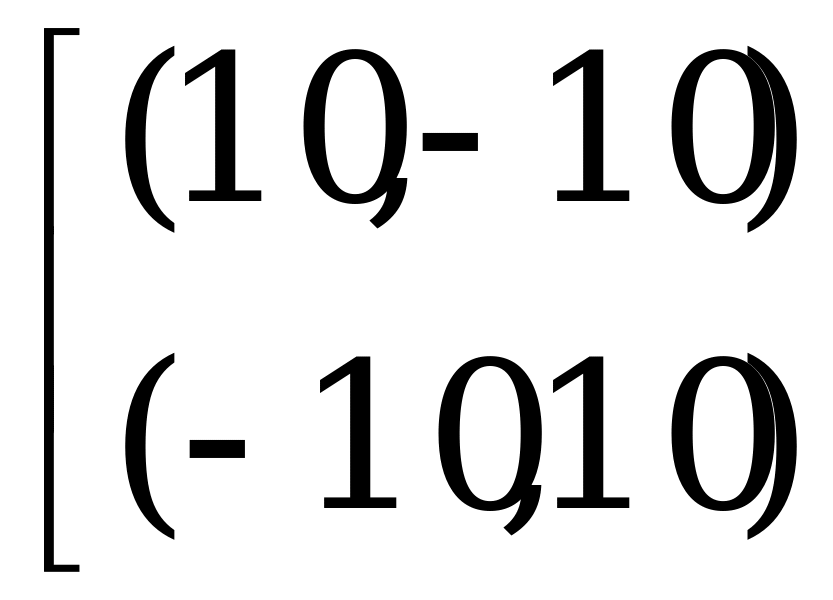
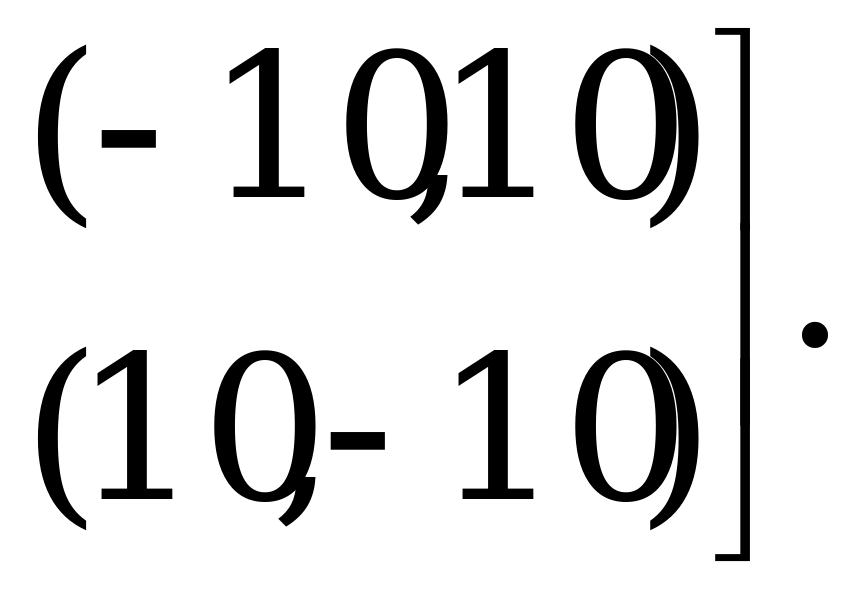
Прямой противоположностью играм с нулевой суммой являются игры с постоянной разностью, в которых игроки выигрывают или проигрывают одновременно. Поэтому им выгодно действовать согласованно.
Пример игры с постоянной разностью. Два человека оказались в горящем доме. Они могут покинуть дом и спастись лишь через входную дверь, которую заклинило так сильно, что открыть её можно только совместными усилиями.
В данном случае каждый из игроков располагает двумя стратегиями:
- толкать дверь и пытаться её открыть;
- не толкать дверь.
Действуя вместе, игроки могут спастись – выигрыш каждого равен 1; в противном случае могут пострадать оба – выигрыш каждого равен 0. Платёжная матрица имеет вид
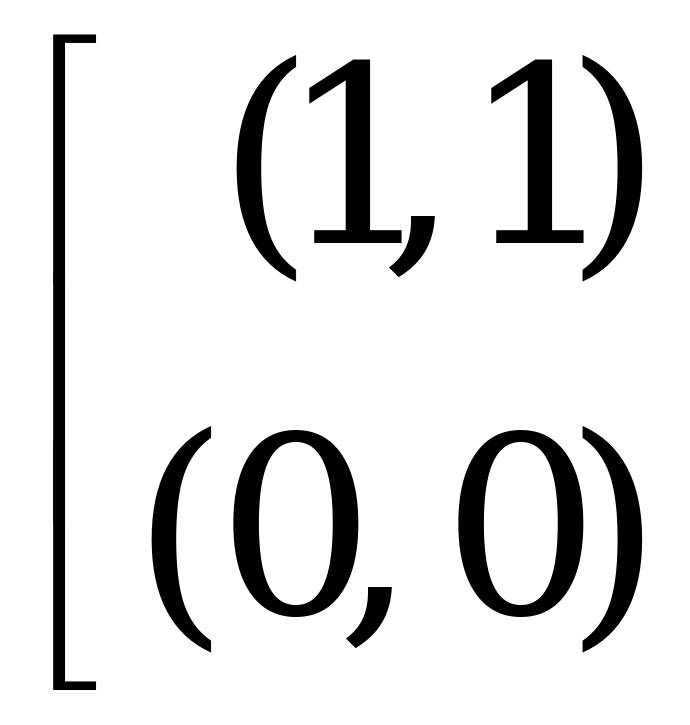
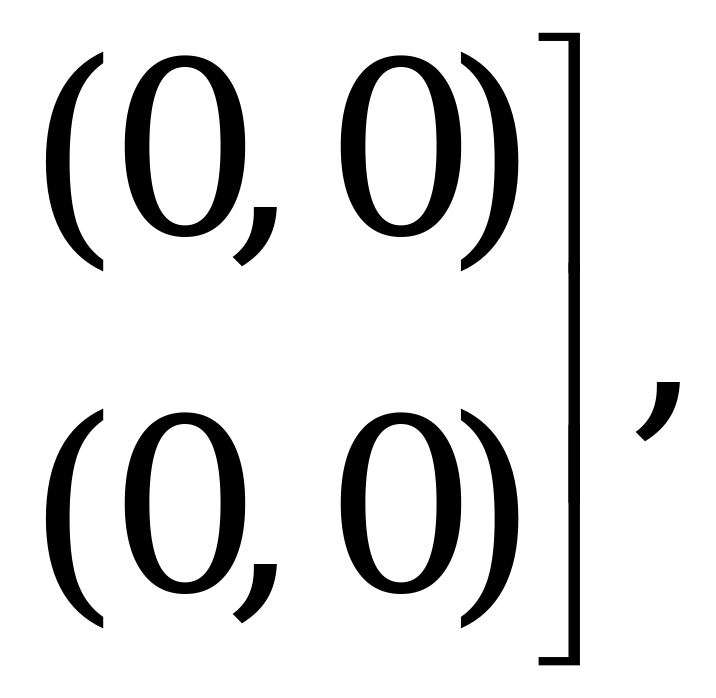
и мы имеем игру с постоянной (нулевой) разностью, в которой игрокам целесообразно координировать свои действия.
Между этими двумя крайними случаями находится множество игр с ненулевой суммой, когда имеются и конфликты, и согласованные действия игроков.
Пример игры с ненулевой суммой. Две фирмы функционируют на рынке одновременно с одинаковым товарным объёмом 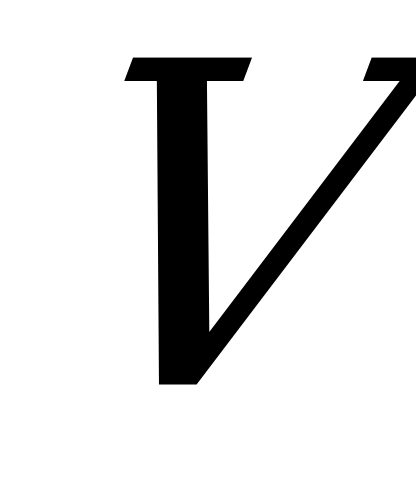 . У обеих фирм по соображениям рентабельности есть следующие стратегии: либо выбросить на рынок полный объём товара
. У обеих фирм по соображениям рентабельности есть следующие стратегии: либо выбросить на рынок полный объём товара 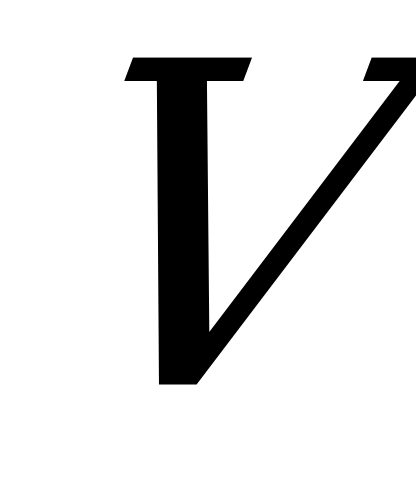 , либо выбросить половину объёма 0,5
, либо выбросить половину объёма 0,5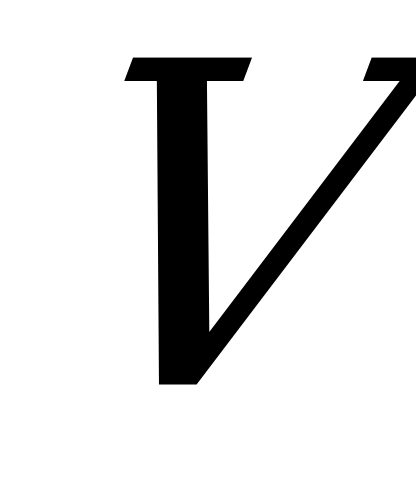 . Если 1-я фирма выбрасывает на рынок полный объём
. Если 1-я фирма выбрасывает на рынок полный объём 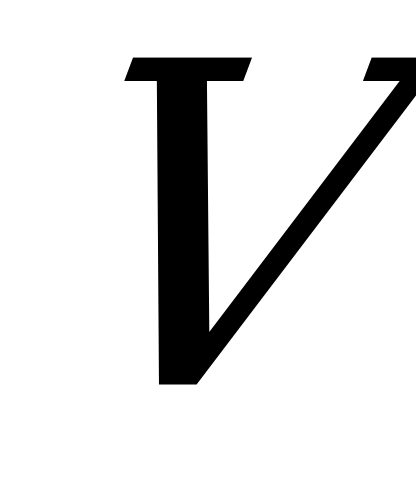 , а 2-я – половину объёма 0,5
, а 2-я – половину объёма 0,5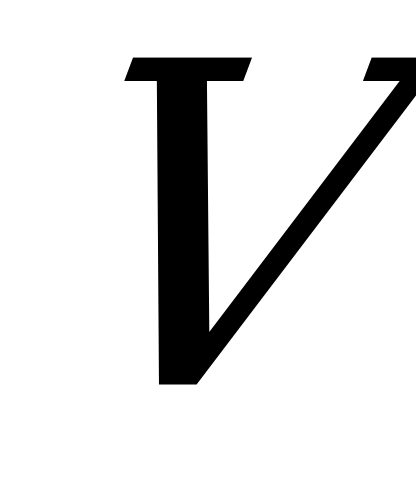 , то 1-я получает 100% запланированной прибыли, а 2-я – только 25%, и наоборот. Если обе фирмы выбросят на рынок по полному объёму
, то 1-я получает 100% запланированной прибыли, а 2-я – только 25%, и наоборот. Если обе фирмы выбросят на рынок по полному объёму 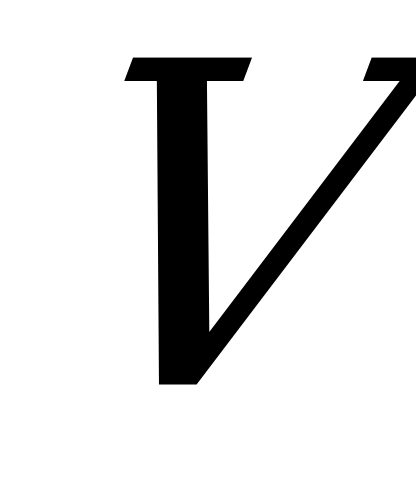 , то получат по 15% прибыли; если по 0,5
, то получат по 15% прибыли; если по 0,5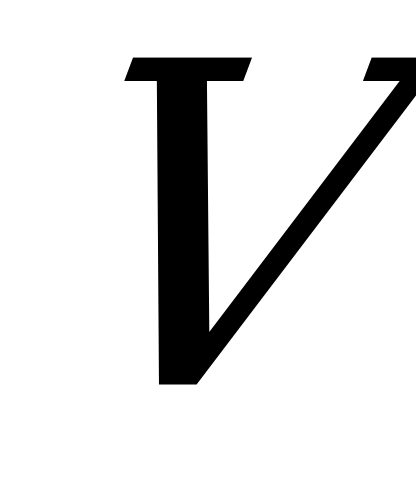 , то прибыль каждой из фирм составит по 50% от запланированной.
, то прибыль каждой из фирм составит по 50% от запланированной.
Биматрица выигрышей для игроков имеет следующий вид:
Стратегии 2-го игрока
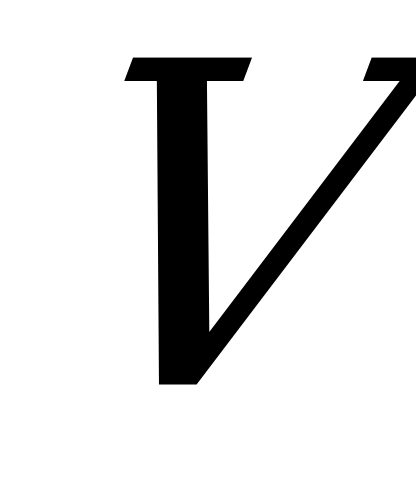 0,5
0,5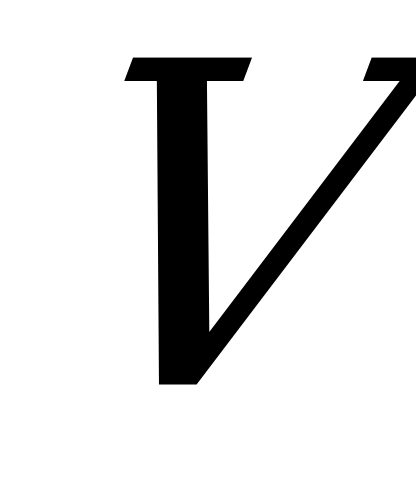
Стратегии 1-го игрока 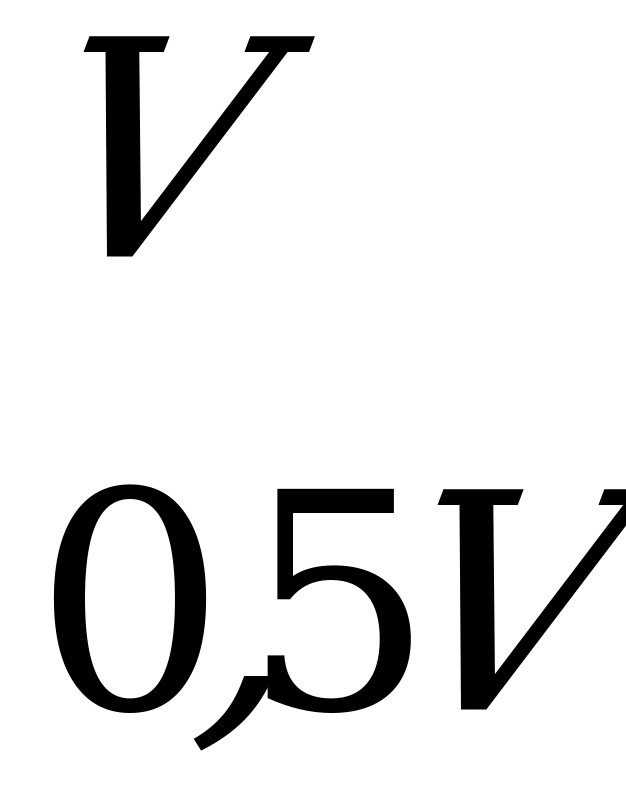
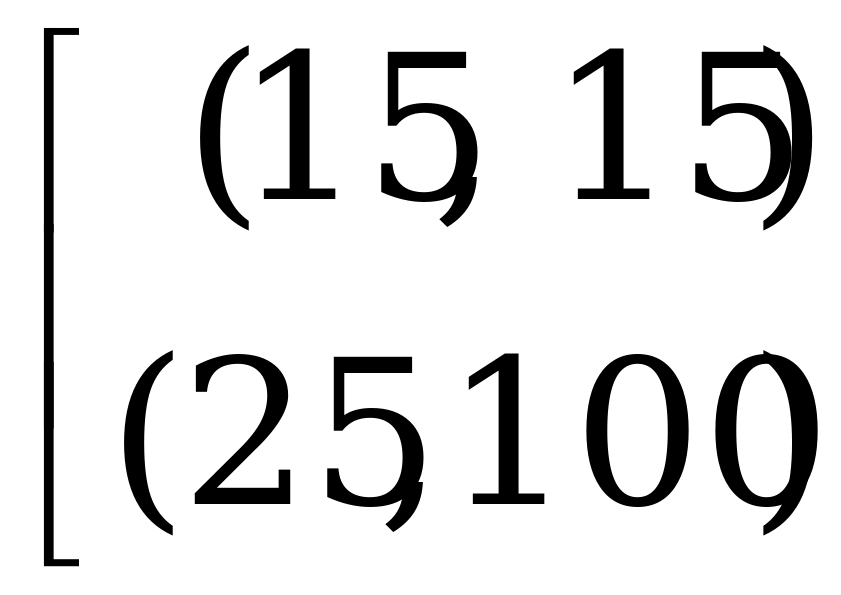
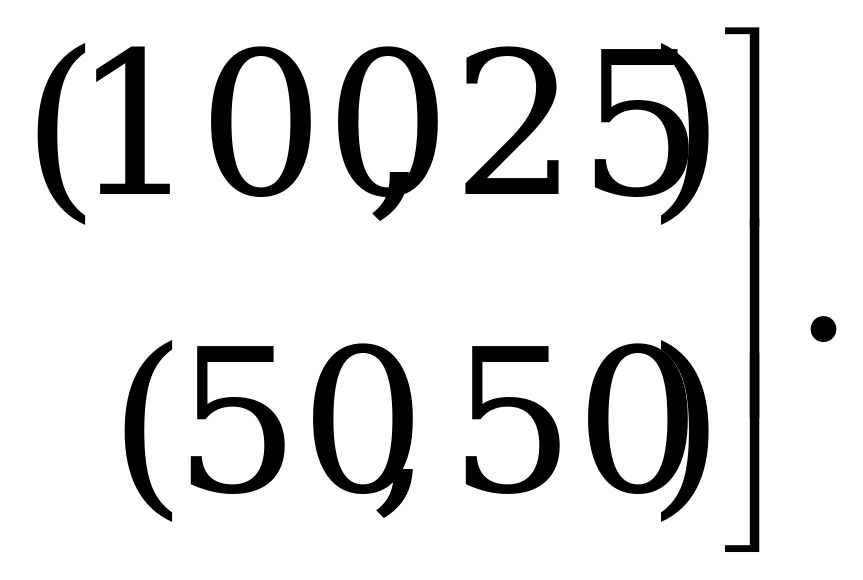
В зависимости от характера предварительной договорённости между игроками различают кооперативные и некооперативные игры. Игра является кооперативной, если до её начала игроки образуют коалиции и принимают взаимообязывающие соглашения о координации своих стратегий. В противном случае игра будет некооперативной.
В зависимости от вида функции выигрышей игры подразделяются на матричные, биматричные, непрерывные, выпуклые, сепарабельные и т.д.
Игры, в которых задаётся последовательность принятия решений игроками, называются позиционными играми. Число игроков в них может варьироваться от двух и более. Если в ранее рассмотренных случаях полагалось, что игроки принимают свои решения одновременно, не зная о решении партнёра, то в данном случае игрок принимает своё решение, уже зная о решении партнёра (соперника), т.е. в ответ на его решение. К позиционным многошаговым играм двух лиц относятся, например, шахматы и шашки. Позиционную игру можно наглядно представить в виде дерева решений.
Игры двух лиц с нулевой суммой
(матричные игры)
Наиболее простые игры – это игры с конечным множеством стратегий.
Пусть у первого игрока (игрока  ) имеется
) имеется 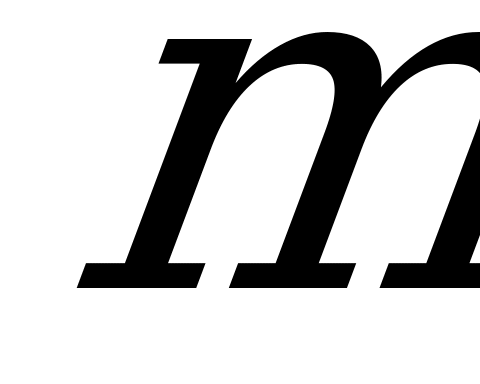 стратегий, а у второго (игрока
стратегий, а у второго (игрока 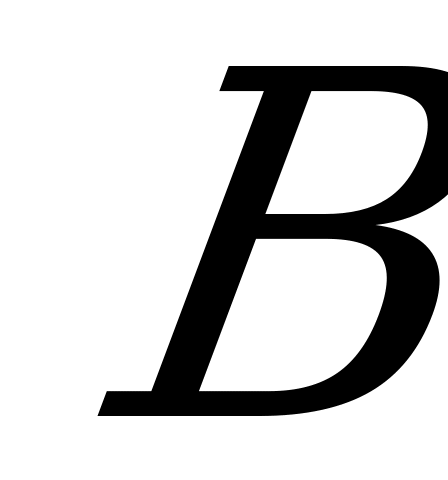 ) -
) - 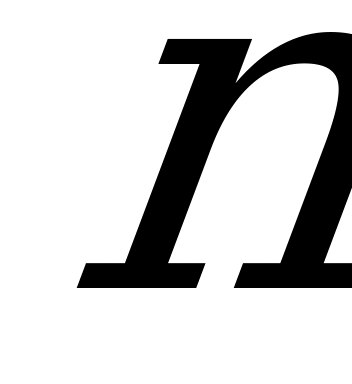 стратегий. Мы можем перенумеровать стратегии каждого из игроков и отождествлять стратегию с её номером. Тогда ситуация – это просто пара номеров
стратегий. Мы можем перенумеровать стратегии каждого из игроков и отождествлять стратегию с её номером. Тогда ситуация – это просто пара номеров  . Значения функций выигрышей
. Значения функций выигрышей 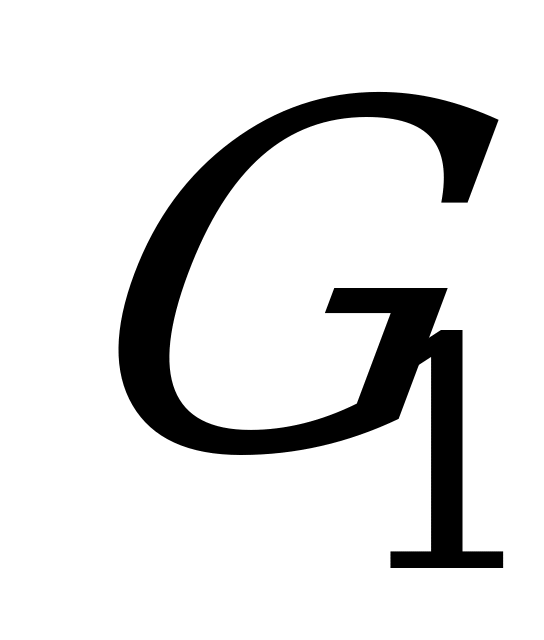 и
и 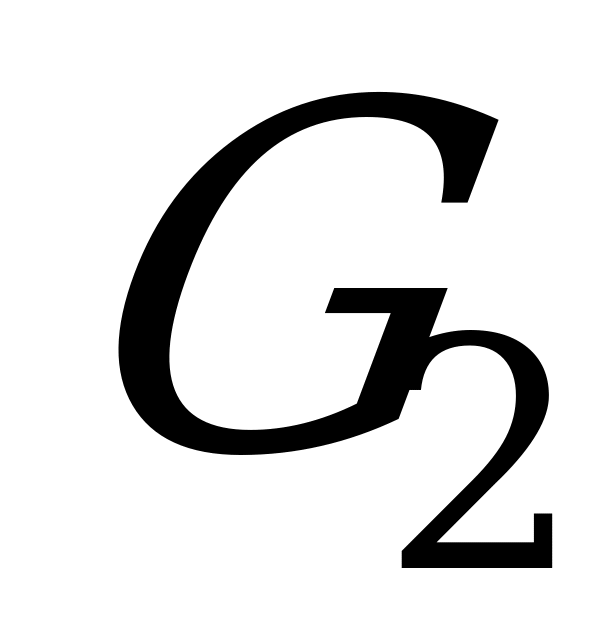 заполнят две матрицы
заполнят две матрицы  и
и 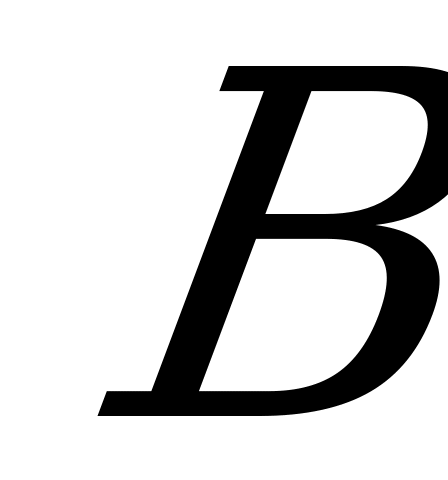 соответственно элементами
соответственно элементами 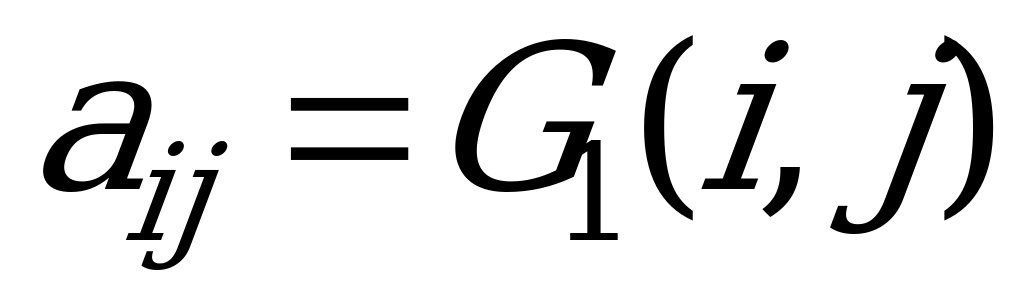 ,
, 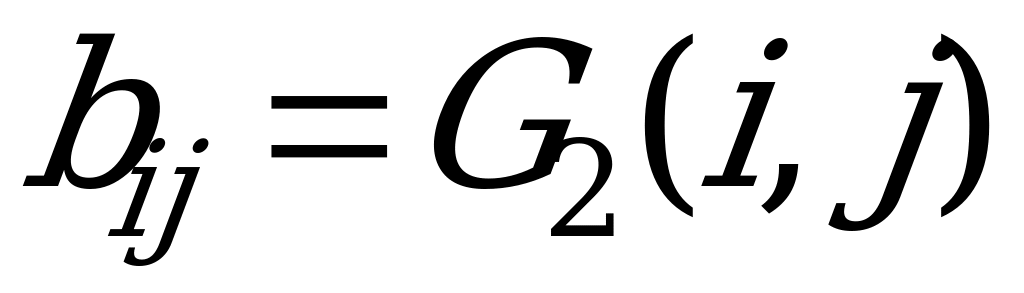 . Если же рассматривается игра с нулевой суммой, то
. Если же рассматривается игра с нулевой суммой, то 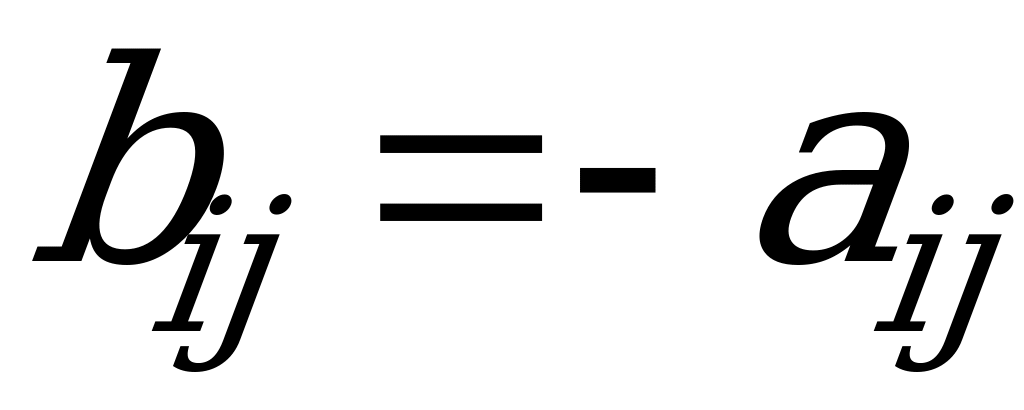 и нужно задать лишь одну матрицу, скажем, матрицу
и нужно задать лишь одну матрицу, скажем, матрицу  . Это и есть класс матричных игр.
. Это и есть класс матричных игр.
Партия игры состоит из двух ходов: игрок  выбирает одну из своих возможных стратегий
выбирает одну из своих возможных стратегий 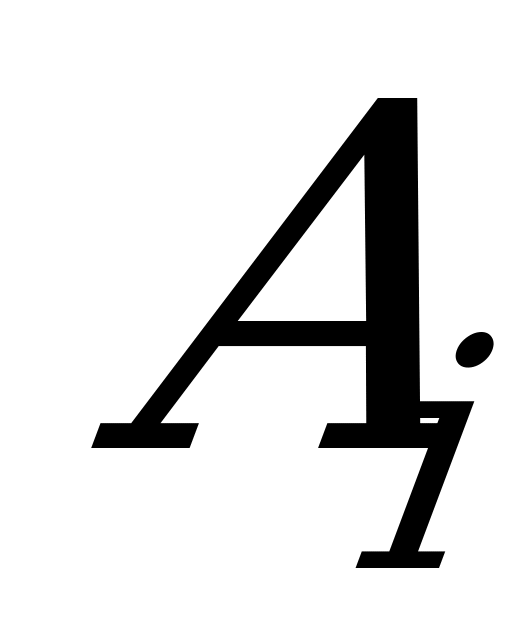
 , а игрок B выбирает стратегию
, а игрок B выбирает стратегию 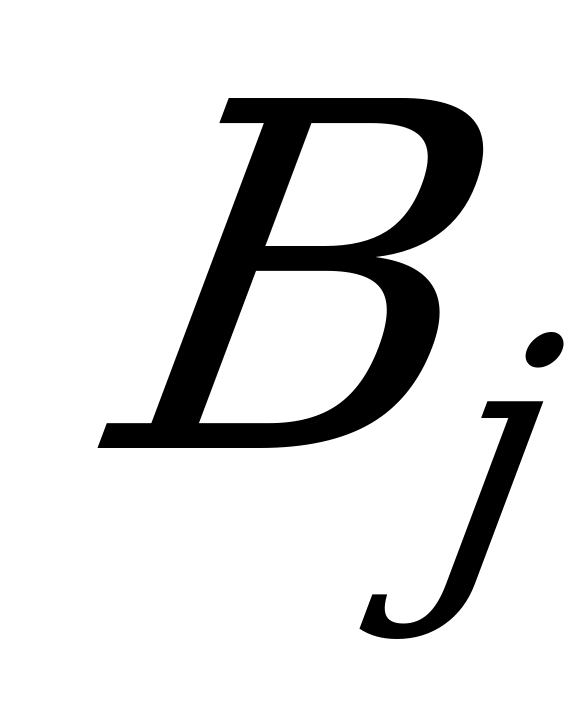
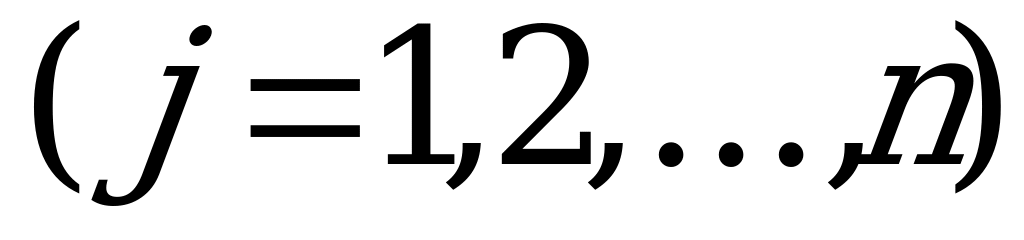 , причём каждый выбор производится при полном незнании выбора другого игрока. Функция выигрышей задаётся матрицей
, причём каждый выбор производится при полном незнании выбора другого игрока. Функция выигрышей задаётся матрицей 


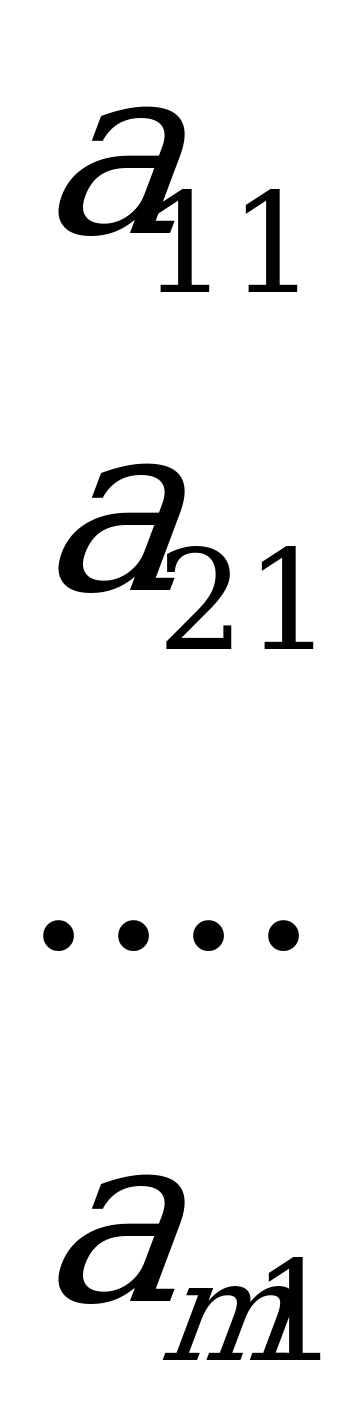


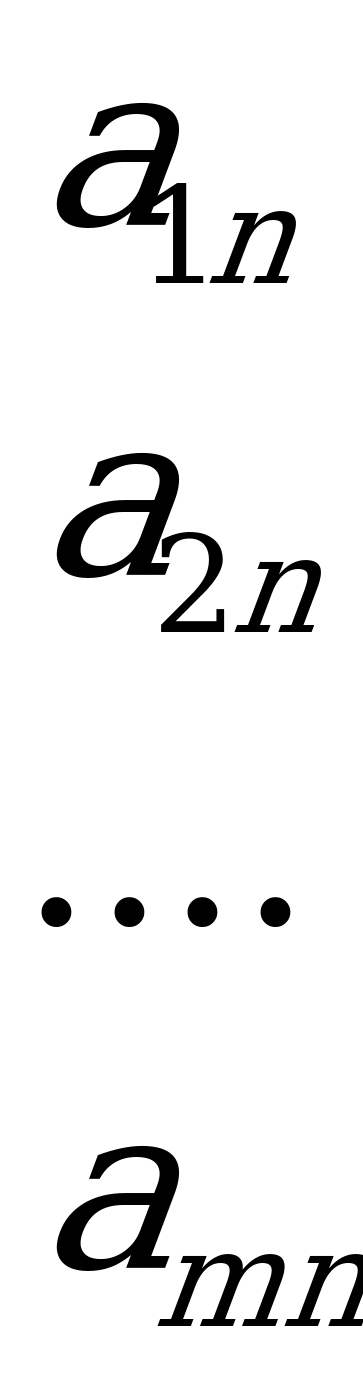
 .
.
Строки матрицы соответствуют стратегиям 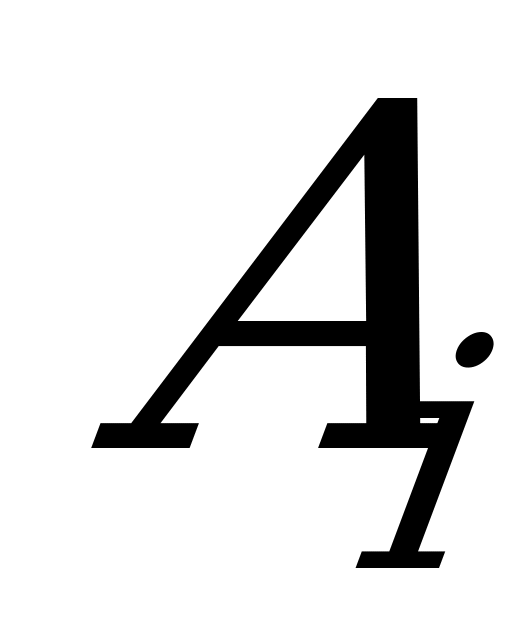 , столбцы – стратегиям
, столбцы – стратегиям 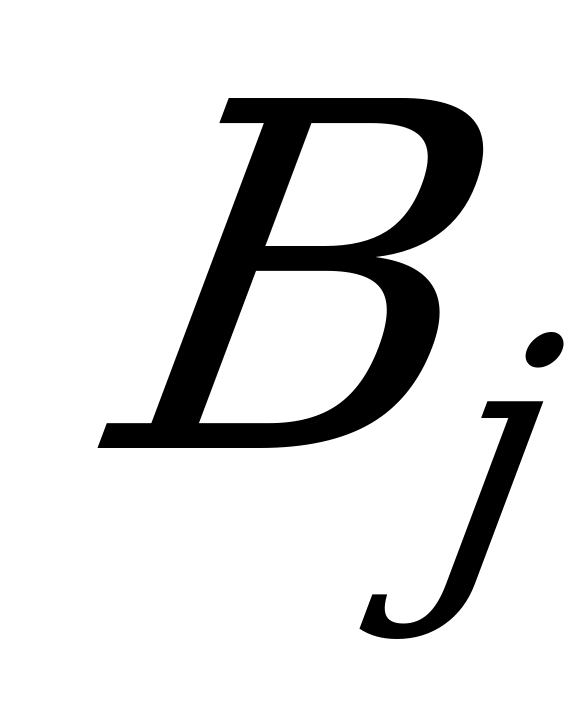 . Элемент
. Элемент  матрицы является действительным числом и представляет собой выигрыш игрока
матрицы является действительным числом и представляет собой выигрыш игрока  (проигрыш игрока
(проигрыш игрока 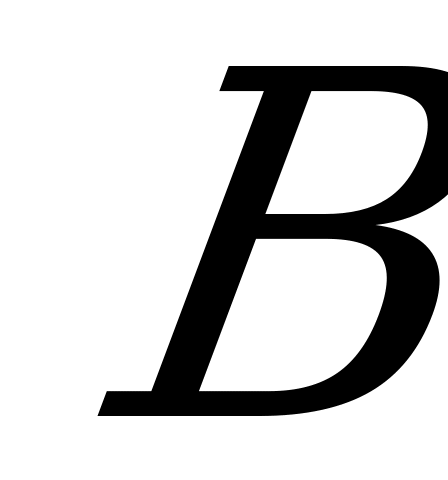 ), если он выбрал стратегию
), если он выбрал стратегию 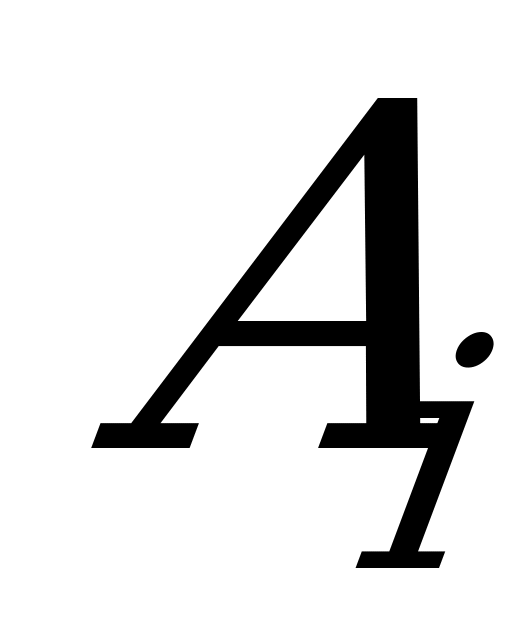 , а игрок
, а игрок 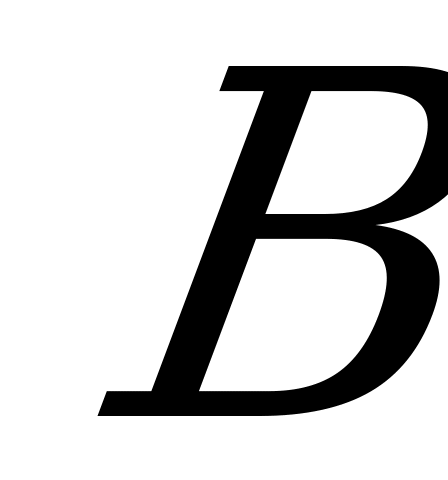 выбрал стратегию
выбрал стратегию 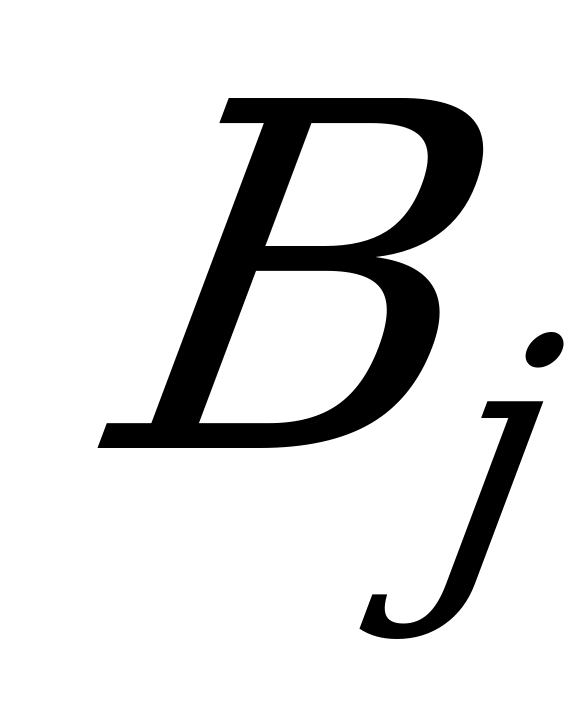 .
.
Пример 1 - а.
Каждый из двух игроков имеет по три монеты достоинством 1 €. Игроки одновременно и независимо друг от друга достают 1, 2 или 3 монеты. При этом, если общее число монет чётное, то выигрывает игрок A, нечётное – игрок B.
Такую игру двух игроков можно представить в виде матрицы







 ,
,
где индекс i элементов 
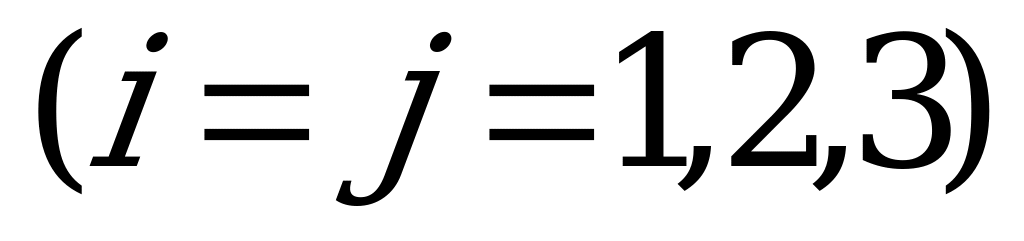 означает количество монет игрока A, а индекс j – количество монет игрока B.
означает количество монет игрока A, а индекс j – количество монет игрока B.
Например,  означает, что одновременно и независимо друг от друга игрок A достал одну монету, а игрок B – 3 монеты. Общее количество монет будет равно четырём, выигрыш игрока A составит 3 € (1 € уже принадлежал игроку A). Элемент
означает, что одновременно и независимо друг от друга игрок A достал одну монету, а игрок B – 3 монеты. Общее количество монет будет равно четырём, выигрыш игрока A составит 3 € (1 € уже принадлежал игроку A). Элемент  означает, что игрок А достал 3 монеты, а игрок В – 2 монеты. Общее число монет будет равно 5, т.е. игрок В выигрывает 3 € (игрок А проигрывает 3 €).
означает, что игрок А достал 3 монеты, а игрок В – 2 монеты. Общее число монет будет равно 5, т.е. игрок В выигрывает 3 € (игрок А проигрывает 3 €).
П ри этом игрок A стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, а игрок B выбирает стратегию, приводящую его к минимальному проигрышу.
ри этом игрок A стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, а игрок B выбирает стратегию, приводящую его к минимальному проигрышу.
Пример 1 - б.
Система противовоздушной обороны (ПВО) обороняет от воздушного налёта участок территории, располагая зенитно-ракетными комплексами (ЗРК), зоны действия которых не перекрываются. Каждый ЗРК с единичной вероятностью поражает самолёт противника в зоне своего действия, если его система наведения начинает отслеживать цель ещё за пределами зоны.
Противник располагает двумя самолётами, каждый из которых может быть направлен в зону действия любого ЗРК. В момент, когда система ПВО решает, какому ЗРК по какой цели стрелять, самолёты противника могут применить обманный маневр и изменить маршрут.
Цель системы ПВО – поразить как можно больше самолётов противника, а цель противника – потерять как можно меньше самолётов.
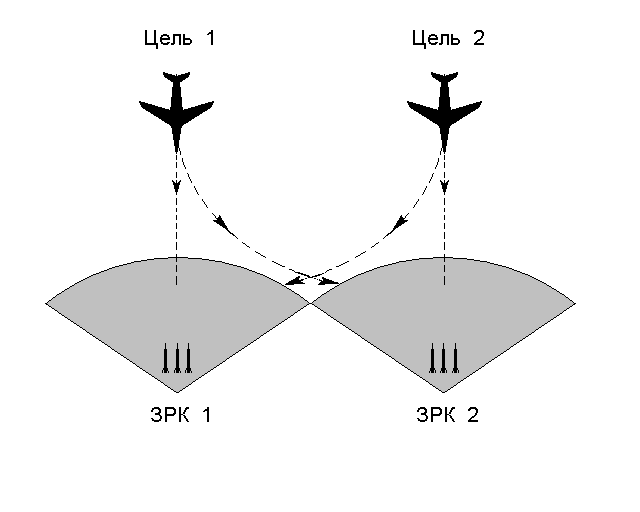
В рассматриваемом случае мы имеем игру двух лиц с нулевой суммой. В распоряжении первого игрока (система ПВО) имеются четыре стратегии:
-
система наведения каждого ЗРК отслеживает цель, направляющуюся в его зону, то есть  -му ЗРК назначена
-му ЗРК назначена  -я цель (
-я цель (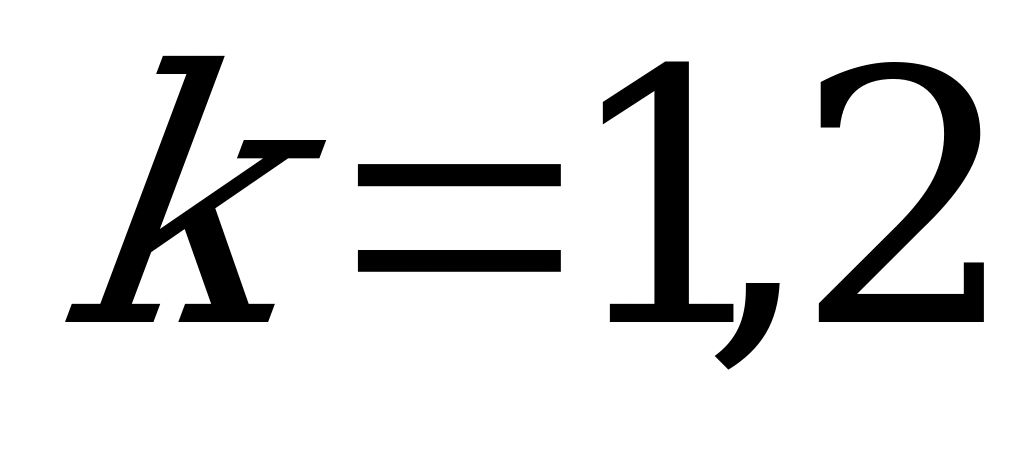 );
);
-
система наведения первого ЗРК отслеживает вторую цель, а система наведения второго ЗРК отслеживает первую цель;
-
системы наведения обоих ЗРК отслеживают первую цель;
-
системы наведения обоих ЗРК отслеживают вторую цель.
У второго игрока (противника) также имеются четыре стратегии:
-
оба самолёта не меняют своего курса, то есть  -й самолёт следует в зону действия
-й самолёт следует в зону действия  -го ЗРК (
-го ЗРК (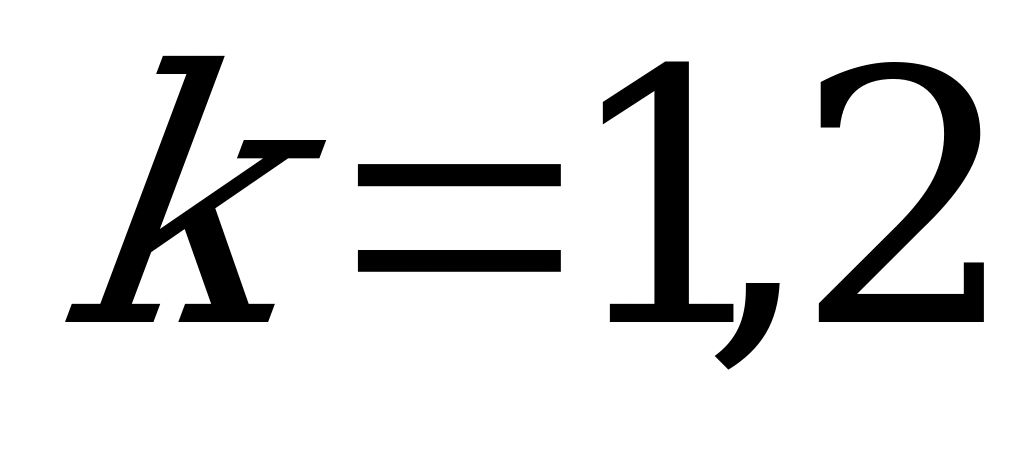 );
);
-
оба самолёта применяют обманный манёвр и меняют курс, то есть первый самолёт следует в зону действия второго ЗРК, а второй самолёт следует в зону действия первого ЗРК;
-
первый самолёт применяет обманный маневр, а второй – нет, то есть оба самолёта следуют в зону действия второго ЗРК;
-
второй самолёт применяет обманный маневр, а первый – нет, то есть оба самолёта следуют в зону действия первого ЗРК.
Платёжная матрица игры имеет вид: 


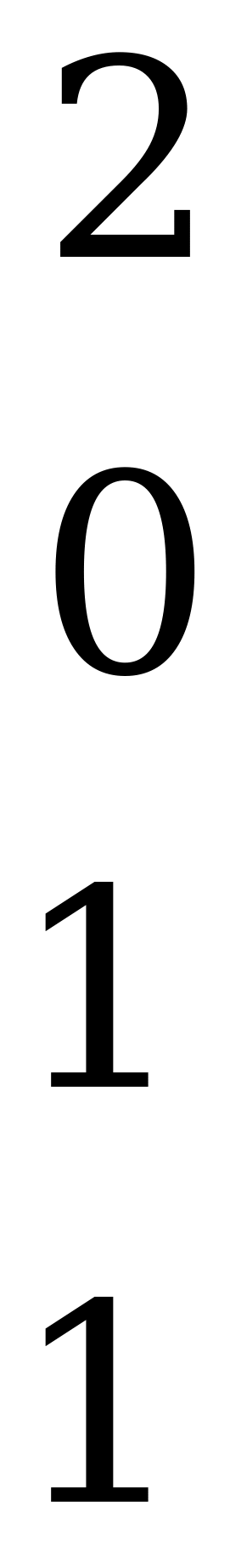
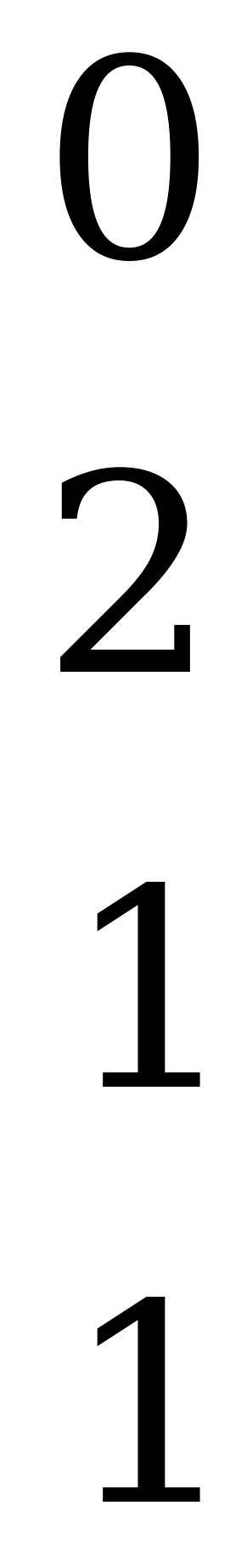


 .
.
Нижняя и верхняя цена игры



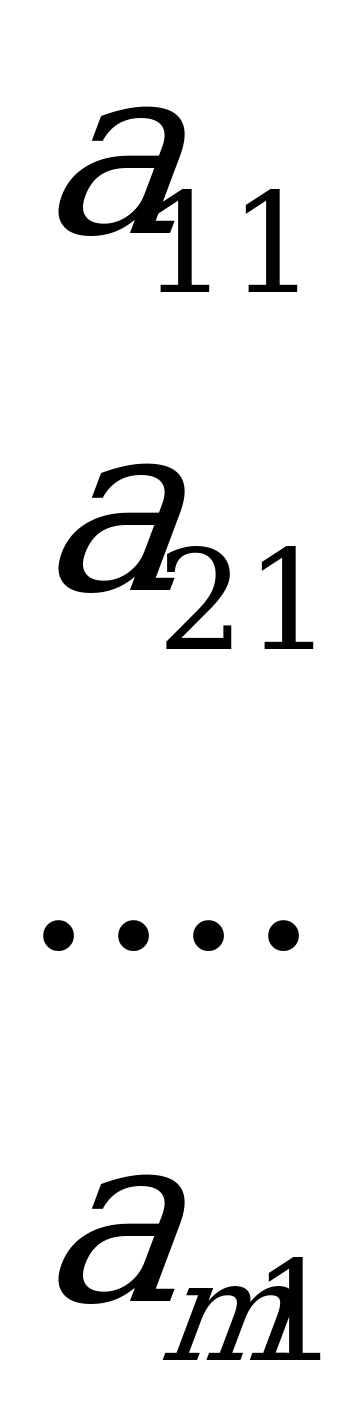


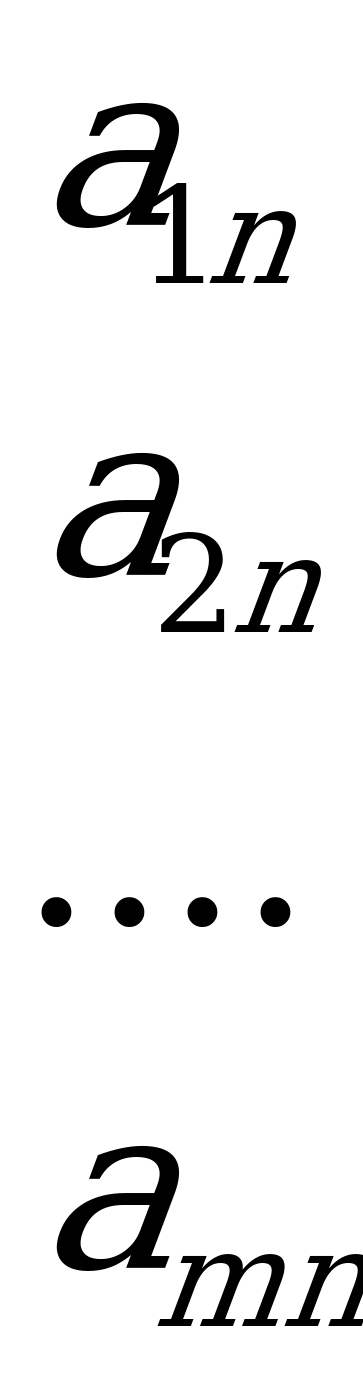
 .
.
Пусть игрок А выбирает некоторую стратегию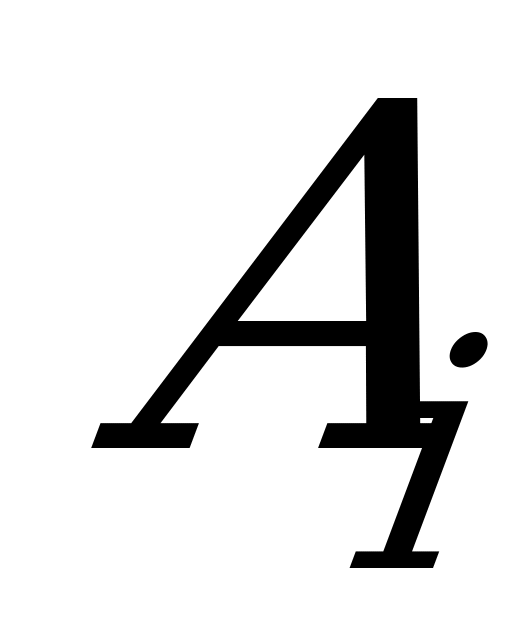 ; тогда в наихудшем случае (например, если выбор станет известным игроку B) он получит выигрыш, равный
; тогда в наихудшем случае (например, если выбор станет известным игроку B) он получит выигрыш, равный  . Предвидя такую возможность, игрок A должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш
. Предвидя такую возможность, игрок A должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш  :
: 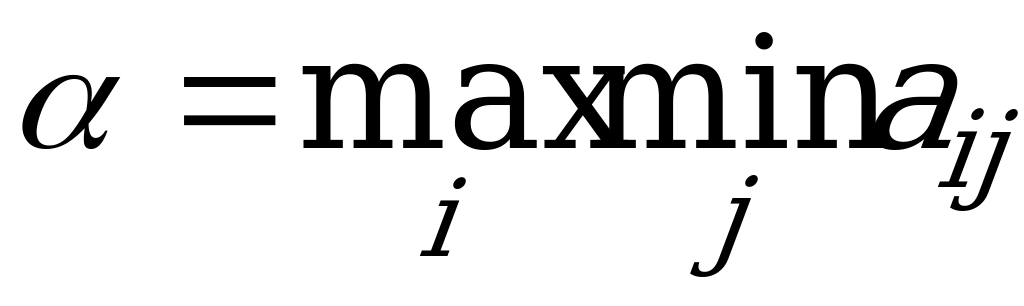 .
.
Это – так называемый «принцип минимакса»: поступай так, чтобы при наихудшем для тебя поведении противника получить максимальный выигрыш.
Величина  - гарантированный выигрыш игрока А - называется нижней ценой игры. Стратегия
- гарантированный выигрыш игрока А - называется нижней ценой игры. Стратегия 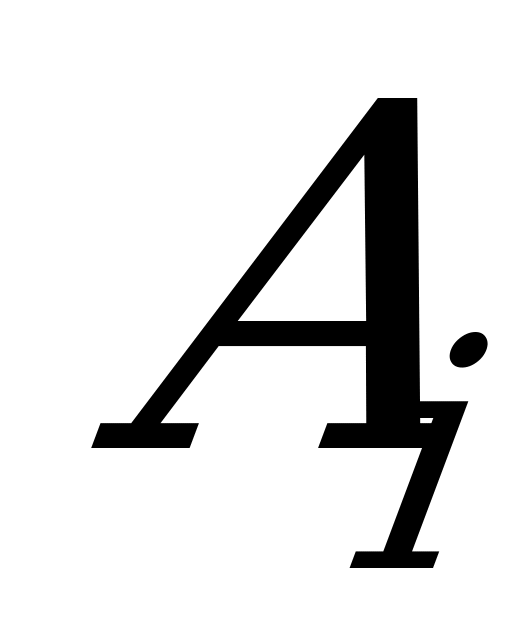 , обеспечивающая получение
, обеспечивающая получение  , называется максиминной.
, называется максиминной.
Игрок B, выбирая стратегию, исходит из следующих соображений: при выборе некоторой стратегии 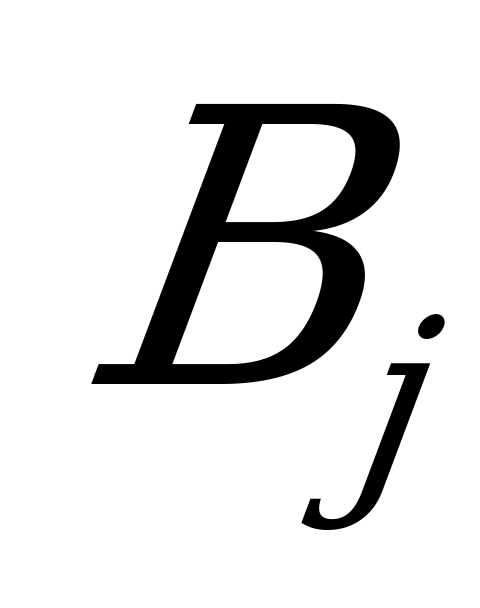 его проигрыш не превысит максимального из значений элементов
его проигрыш не превысит максимального из значений элементов  -го столбца матрицы. Рассматривая множество
-го столбца матрицы. Рассматривая множество 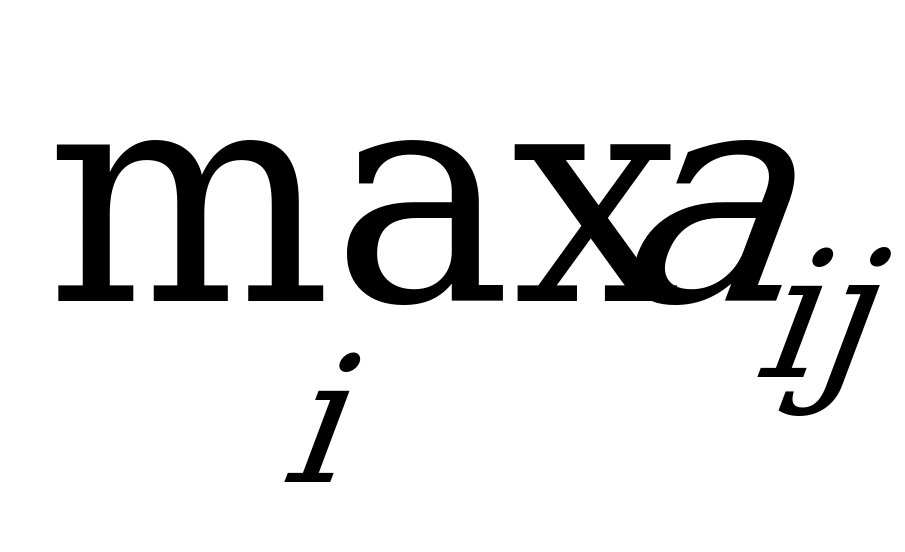 для различных значений
для различных значений  , игрок B, естественно, выберет такое значение
, игрок B, естественно, выберет такое значение  , при котором его максимальный проигрыш
, при котором его максимальный проигрыш 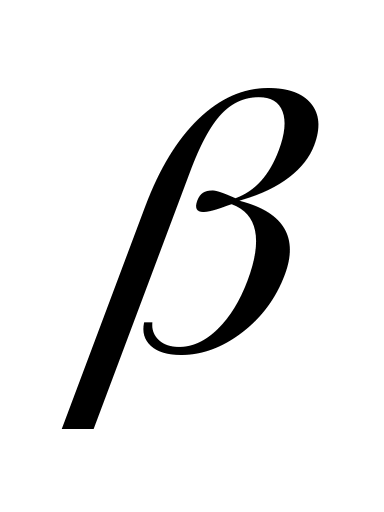 минимизируется :
минимизируется :  .
.
Величина 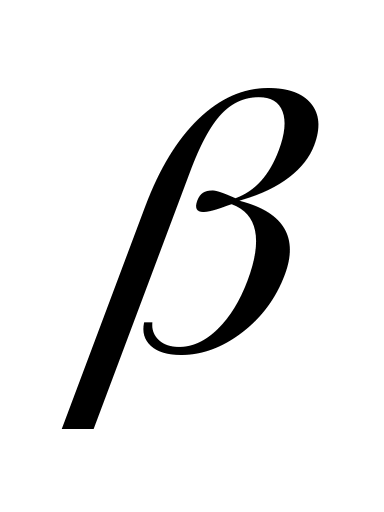 называется верхней ценой игры, а соответствующая выигрышу
называется верхней ценой игры, а соответствующая выигрышу 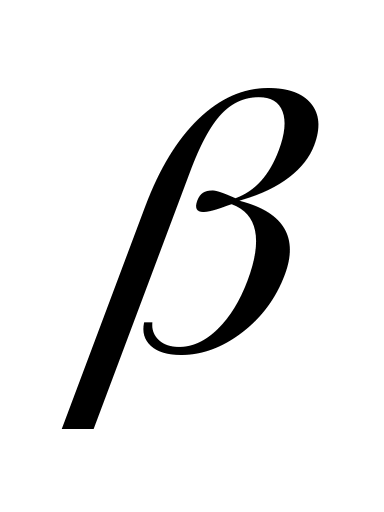 стратегия
стратегия 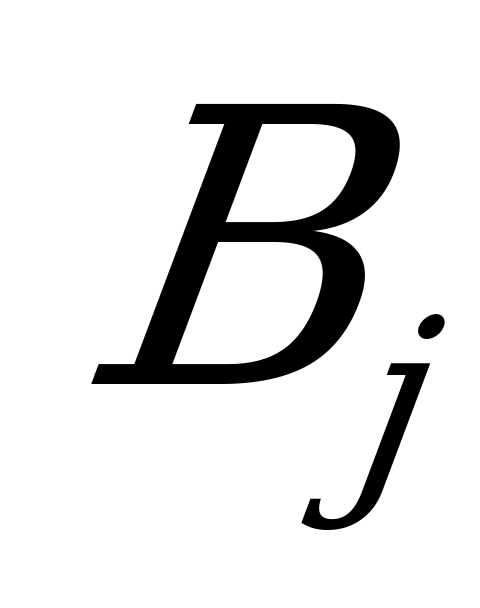 - минимаксной.
- минимаксной.
Если 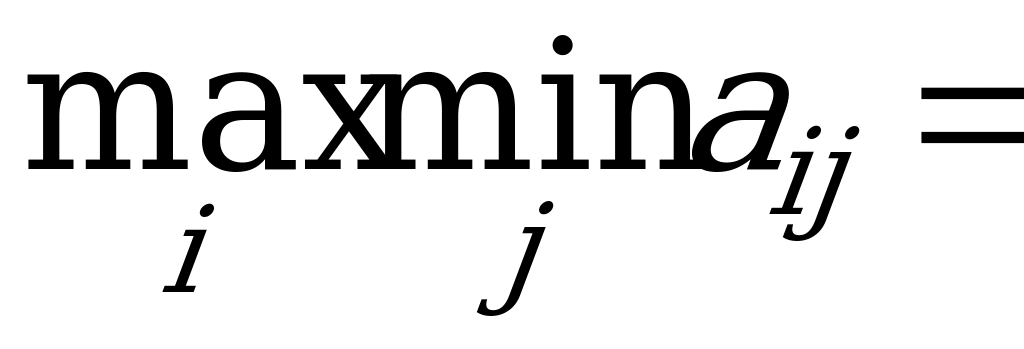
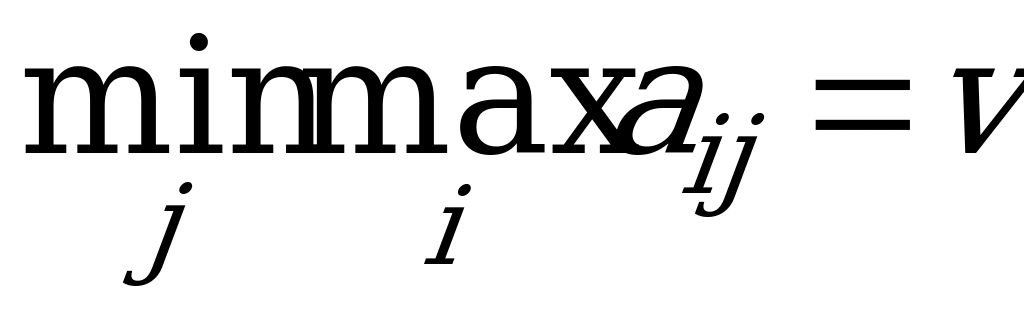 , то выигрыш игрока A – вполне определённое число
, то выигрыш игрока A – вполне определённое число  , которое называется ценой игры. Элемент
, которое называется ценой игры. Элемент  в матрице такой игры, являющийся одновременно минимальным в своей строке
в матрице такой игры, являющийся одновременно минимальным в своей строке  и максимальным в своём столбце
и максимальным в своём столбце  , называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность – это решение игры.
, называется седловой точкой. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность – это решение игры.
Термин «седловая точка» взят из геометрии – так называется точка на поверхности, где одновременно достигается минимум по одной координате и максимум по другой. Заметим, что седловая точка может быть и не единственной (так, платёжная матрица игры из примера 1-б имеет четыре седловые точки, расположенные на пересечении двух её последних строк и двух последних столбцов).
В теории игр элементы множеств допустимых решений игроков принято называть чистыми стратегиями. В игре двух лиц с нулевой суммой при наличии седловой точки решение игры находится в чистых стратегиях.
Решение для игрока записывается в виде набора чисел 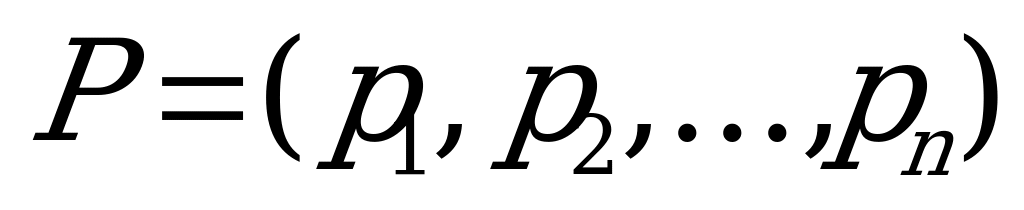 , где
, где 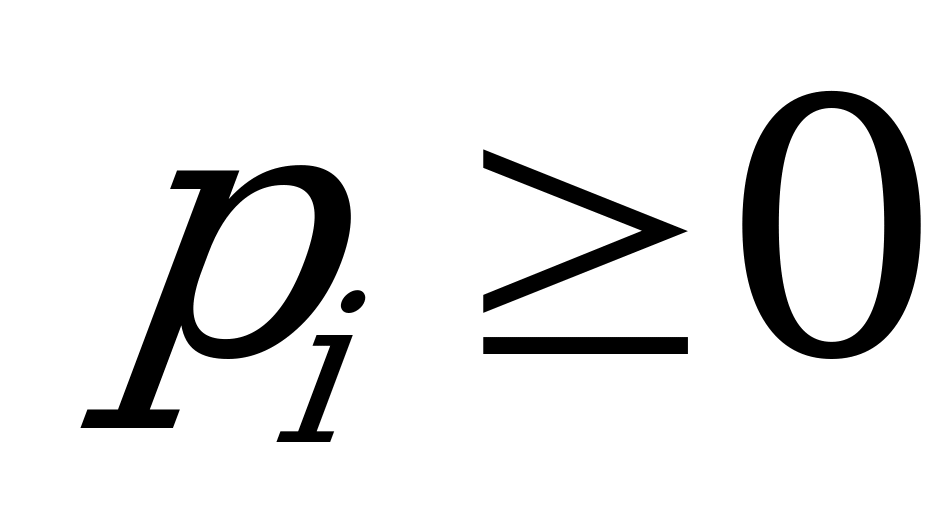
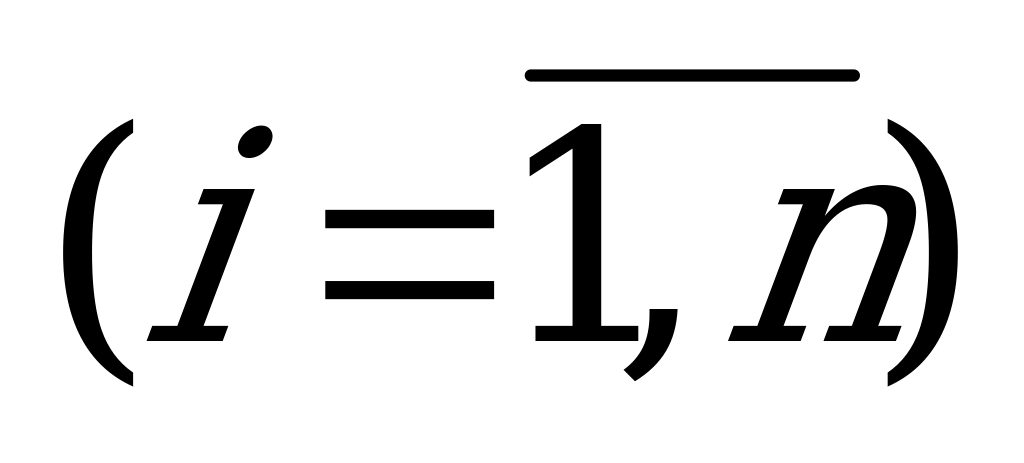 и
и 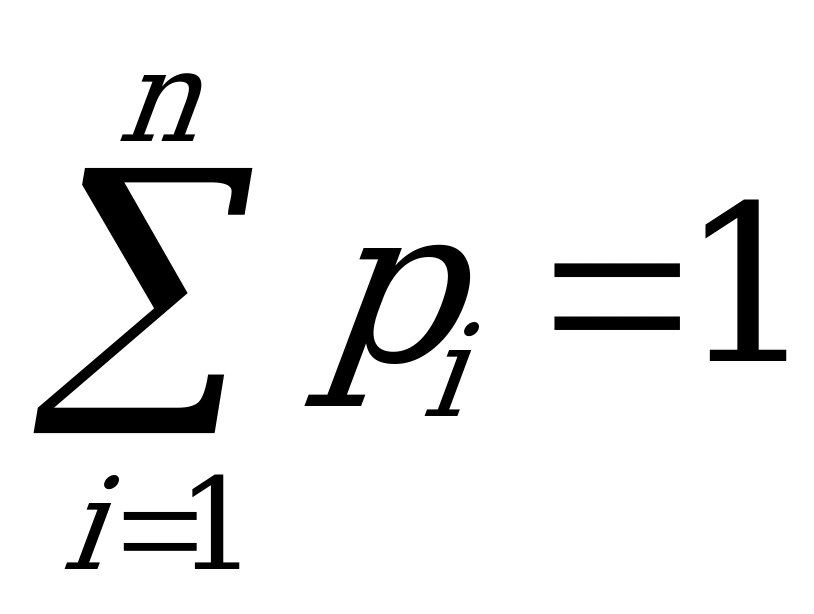 . Число
. Число 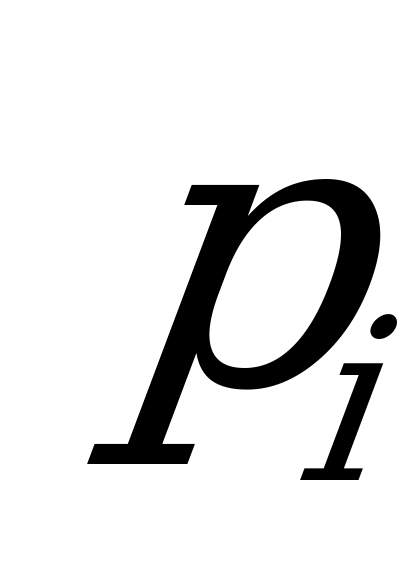 означает вероятность применения игроком
означает вероятность применения игроком  ой чистой стратегии.
ой чистой стратегии.
Решение игры в чистых стратегиях 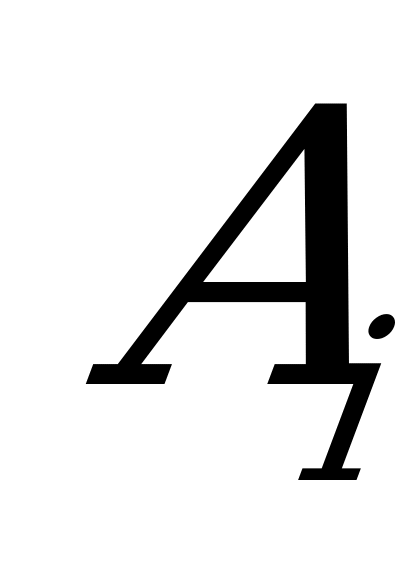 и
и 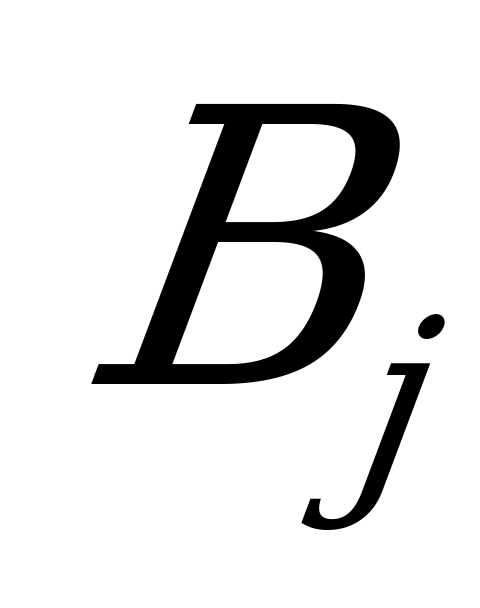 можно записать в виде:
можно записать в виде:
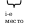
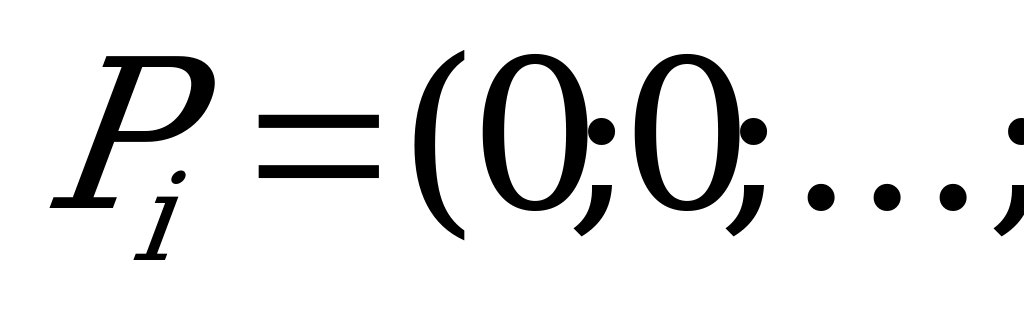
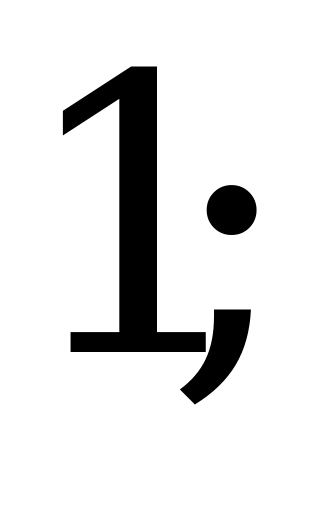
 ,
, 
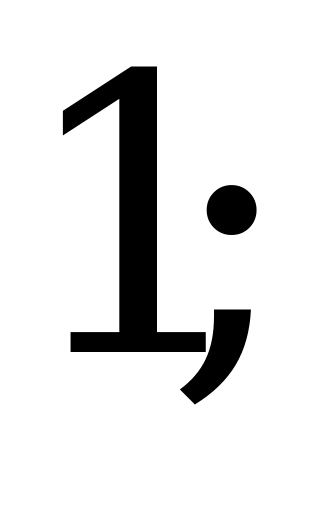
 .
.
Стратегии игрока, для которых вероятности 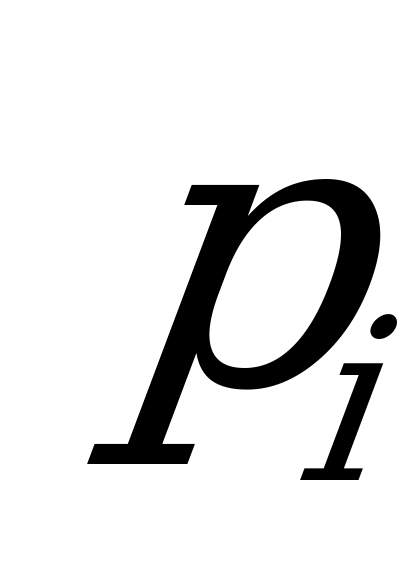 отличны от нуля, называются активными.
отличны от нуля, называются активными.
П
В данном случае матрица игры содержит седловую точку, поэтому оптимальными стратегиями для игроков являются их минимаксные стратегии (игра решается в чистых стратегиях): 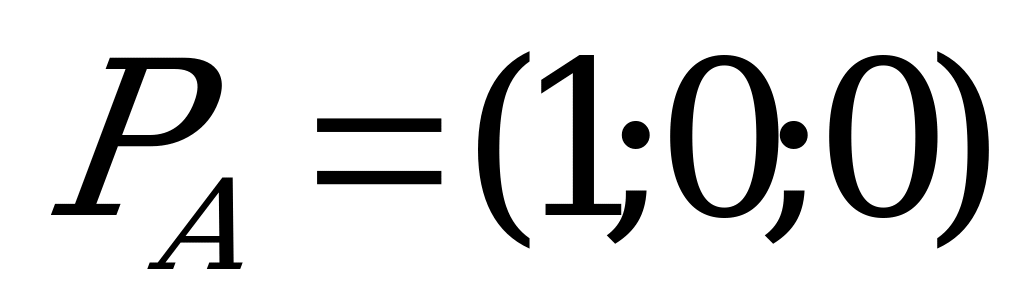 ,
, 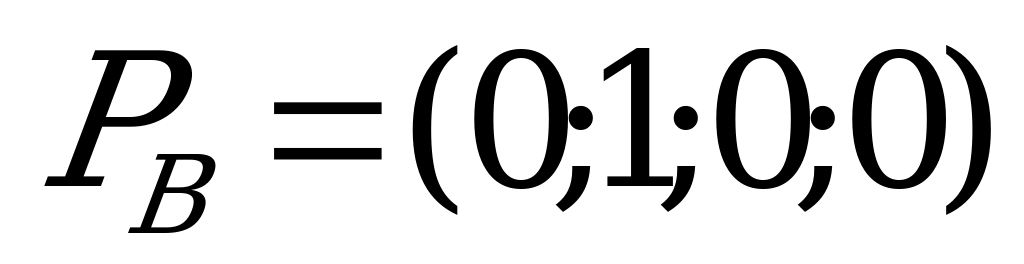 .
.
ример 2.




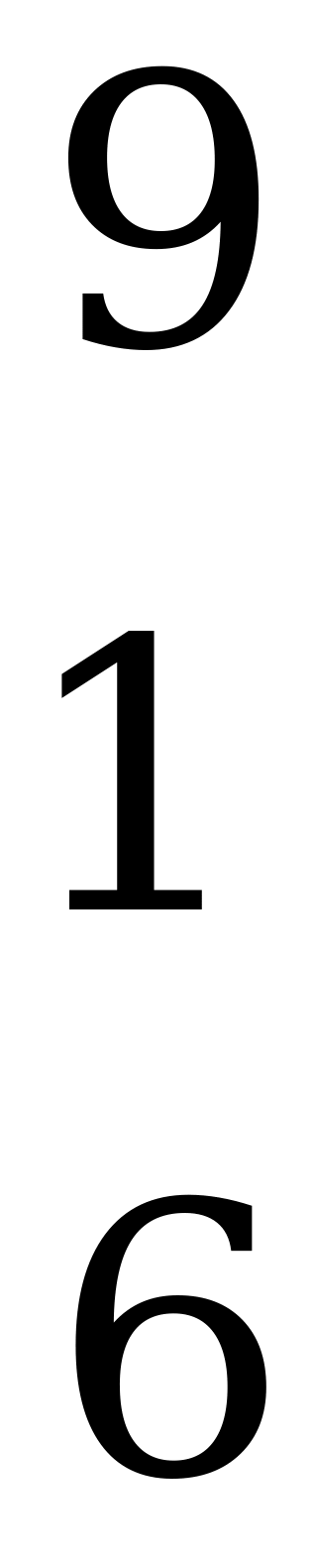
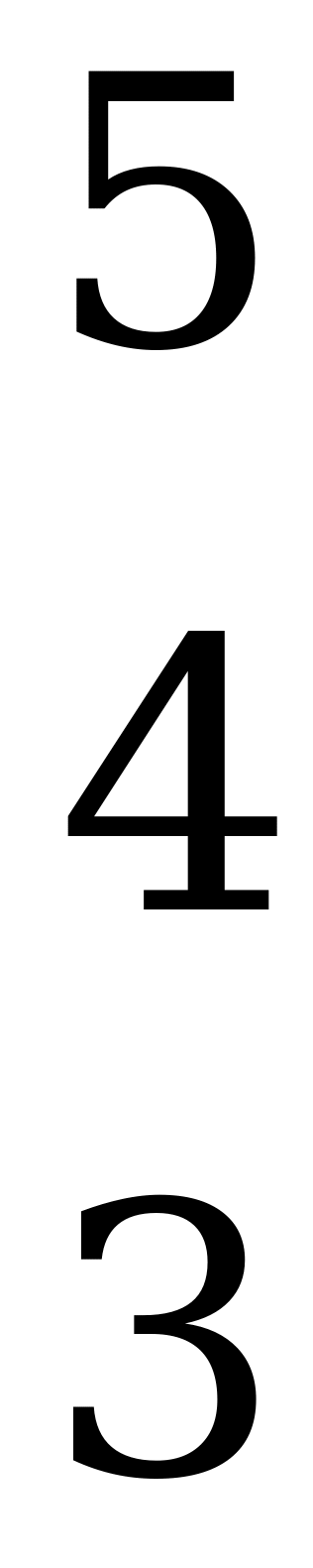
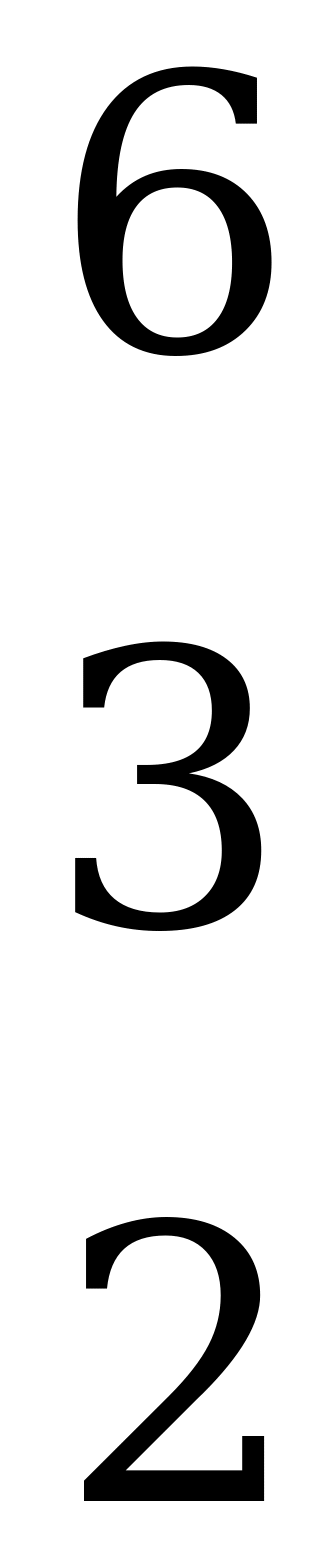

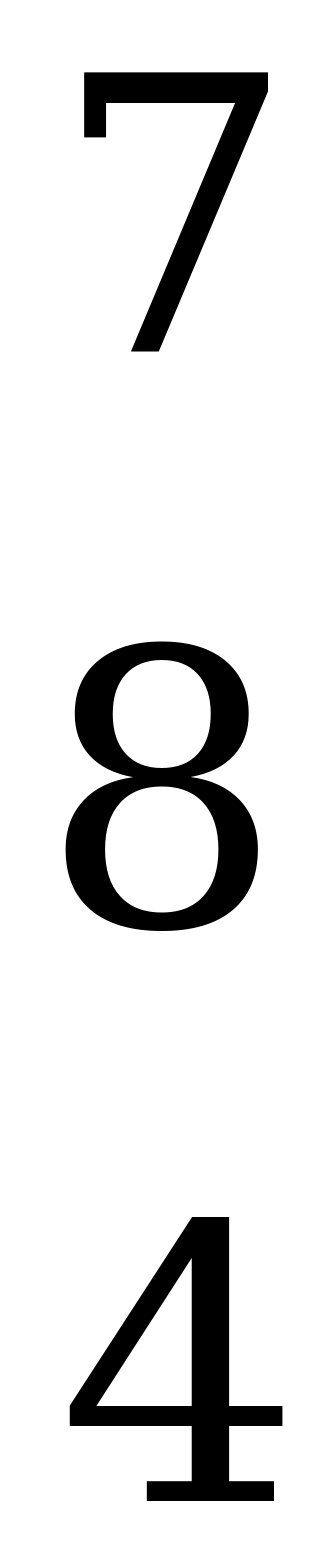

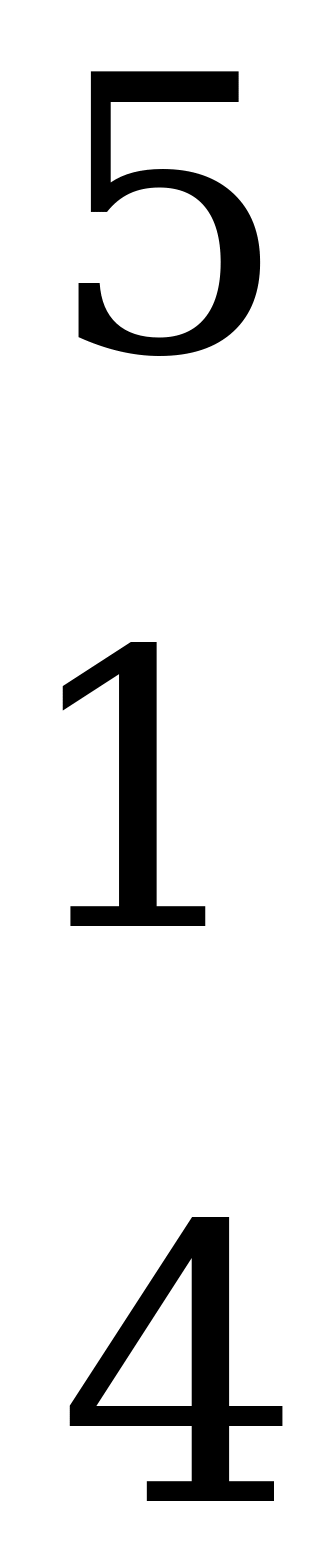
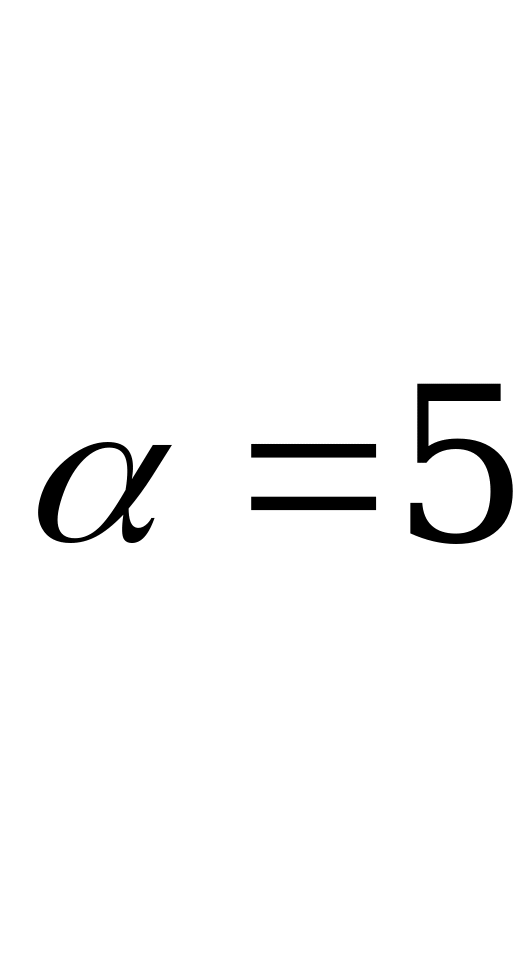
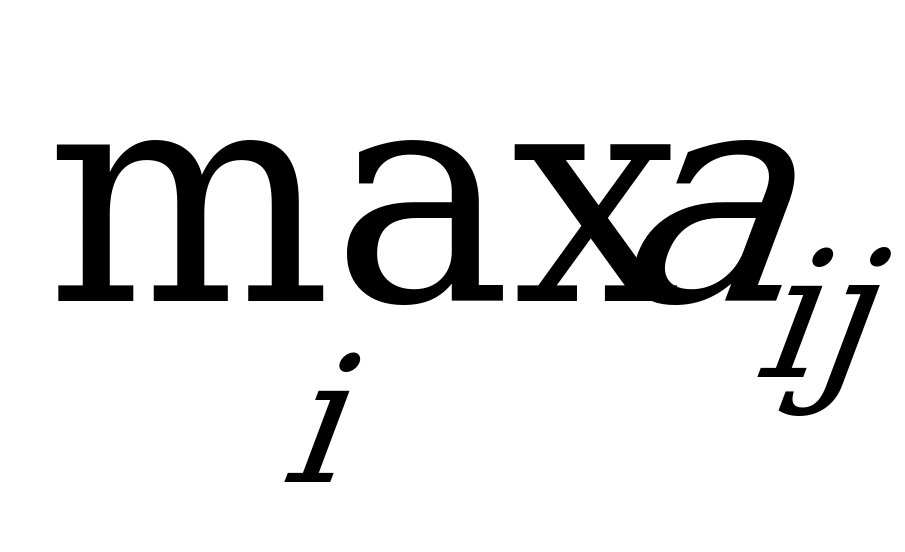
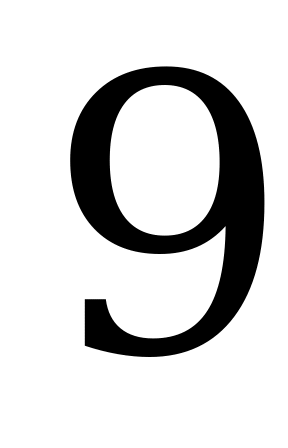


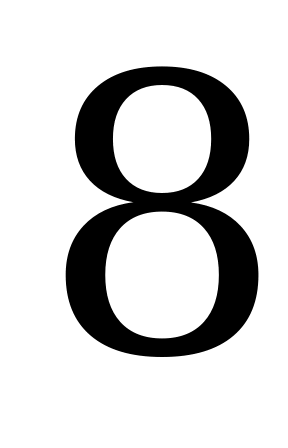


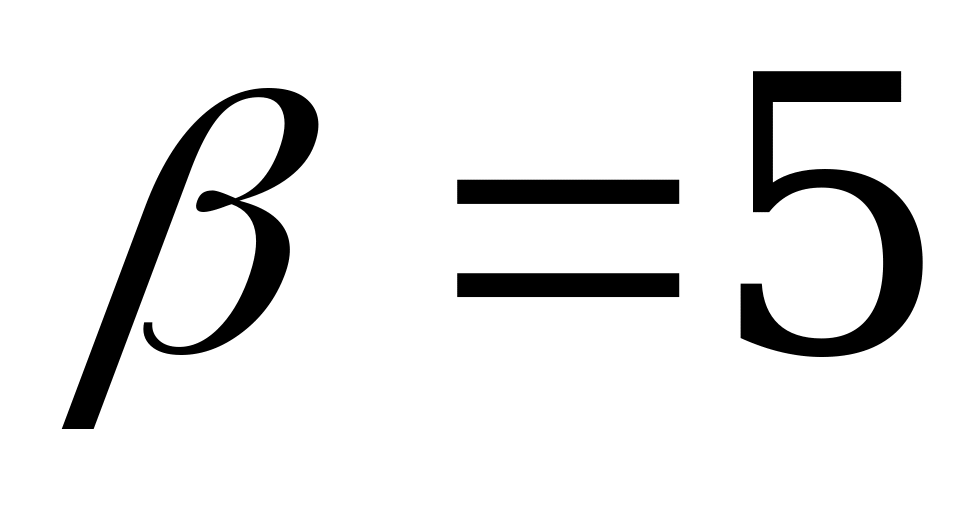
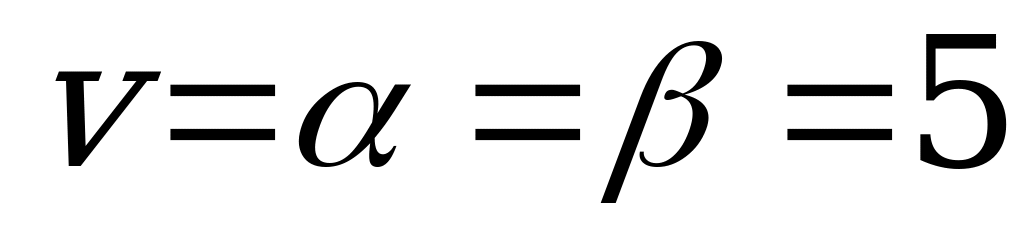
Пример 3. 

Данная матрица не содержит седловой точки.



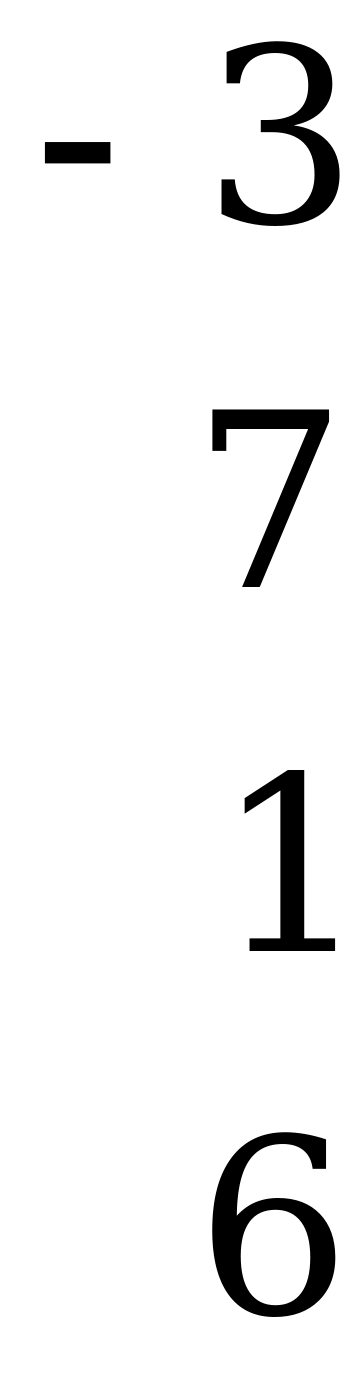



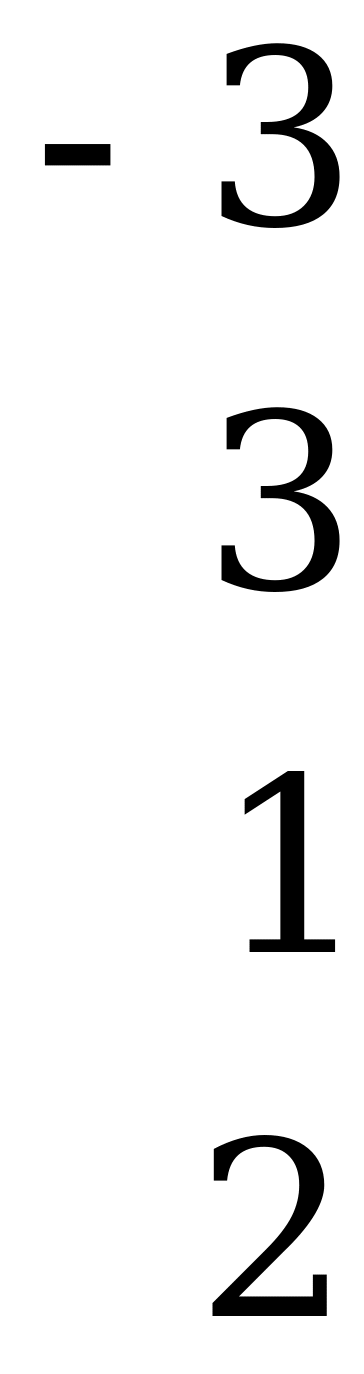

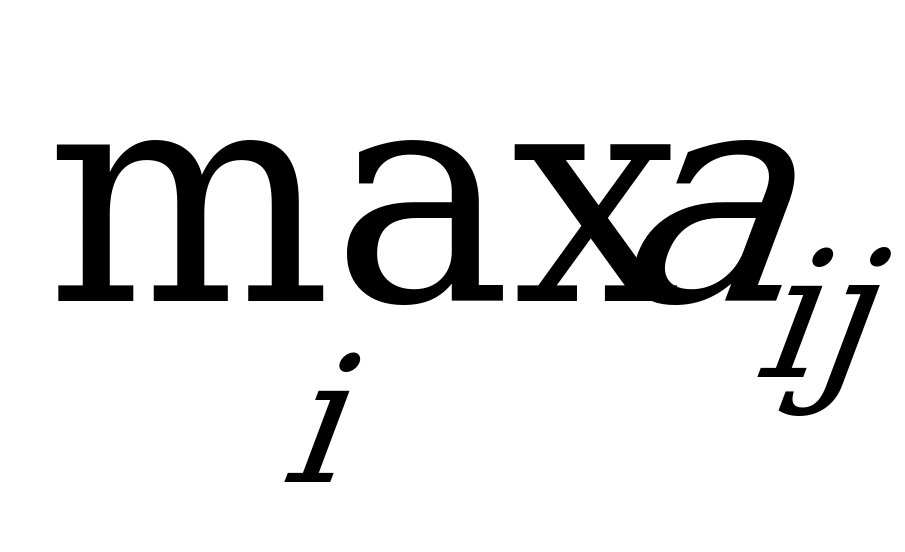




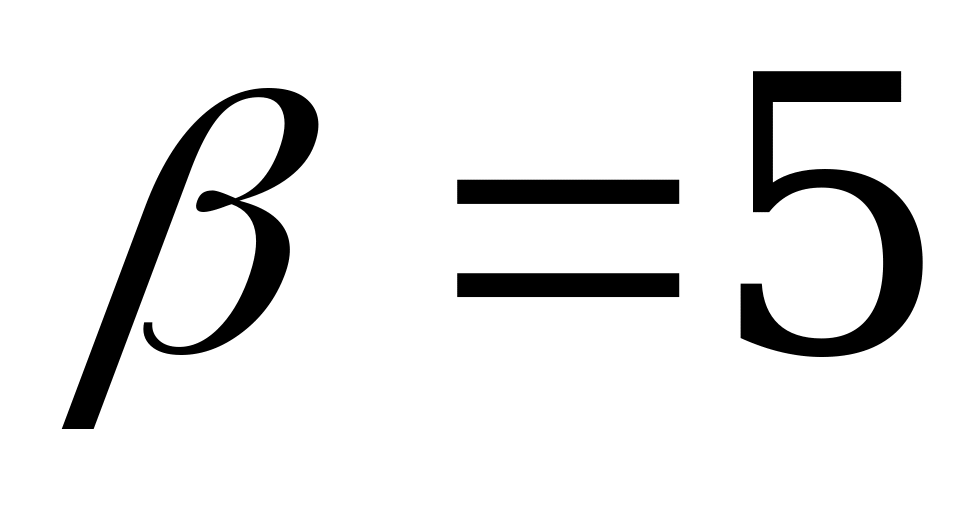
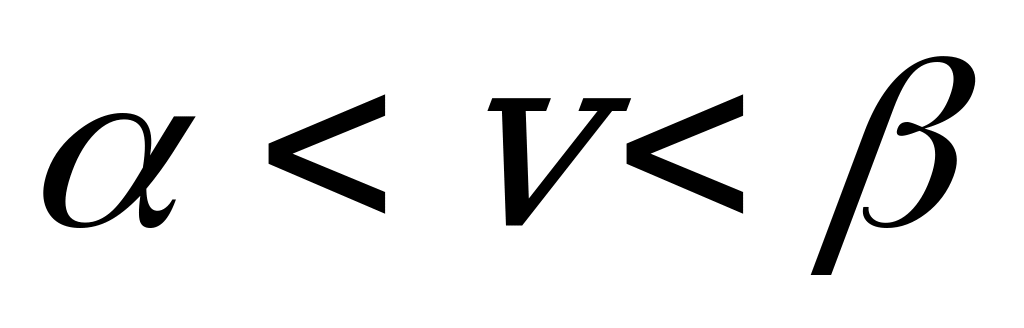
Основная теорема теории игр
Любая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.
Применение игроком A оптимальной стратегии позволяет получить (при любых действиях игрока B) выигрыш не меньше цены игры  .
.
Если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей.
Методы решения конечных игр
Задача решения игры, если её матрица не содержит седловой точки, тем сложней, чем больше значения 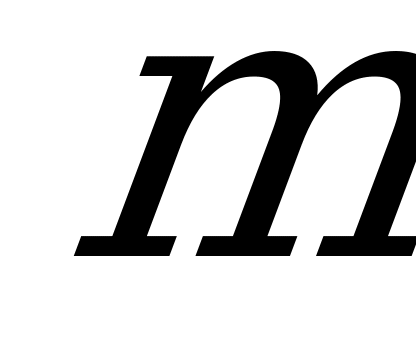 и
и 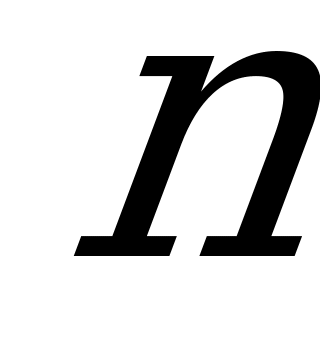 . Поэтому в теории матричных игр рассматриваются способы, с помощью которых решение одних игр сводится к решению других, более простых (в частности, с помощью сокращения размерности матрицы). Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные стратегии.
. Поэтому в теории матричных игр рассматриваются способы, с помощью которых решение одних игр сводится к решению других, более простых (в частности, с помощью сокращения размерности матрицы). Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные стратегии.
Дублирующими называются стратегии, которым соответствуют одинаковые значения элементов в платёжной матрице, то есть матрица содержит одинаковые строки (столбцы).
Если элементы 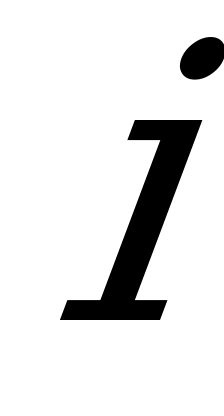 -ой строки матрицы не меньше соответствующих элементов
-ой строки матрицы не меньше соответствующих элементов  -й строки и хотя бы один элемент больше соответствующего элемента
-й строки и хотя бы один элемент больше соответствующего элемента  -й строки, то
-й строки, то 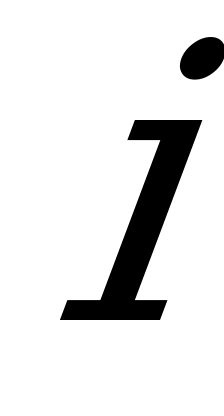 -я стратегия для игрока A называется доминирующей. Если же элементы
-я стратегия для игрока A называется доминирующей. Если же элементы  -го столбца матрицы не больше соответствующих элементов
-го столбца матрицы не больше соответствующих элементов 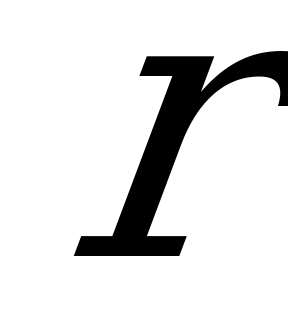 -го столбца и, по крайней мере, один из них меньше, то для игрока B стратегия
-го столбца и, по крайней мере, один из них меньше, то для игрока B стратегия  - доминирующая.
- доминирующая.
Пример 4. 


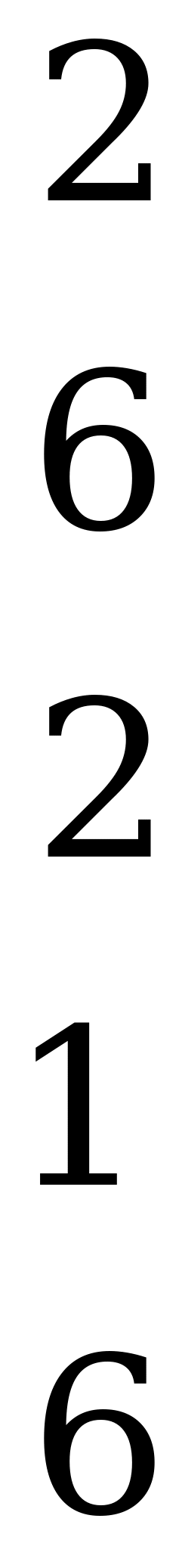
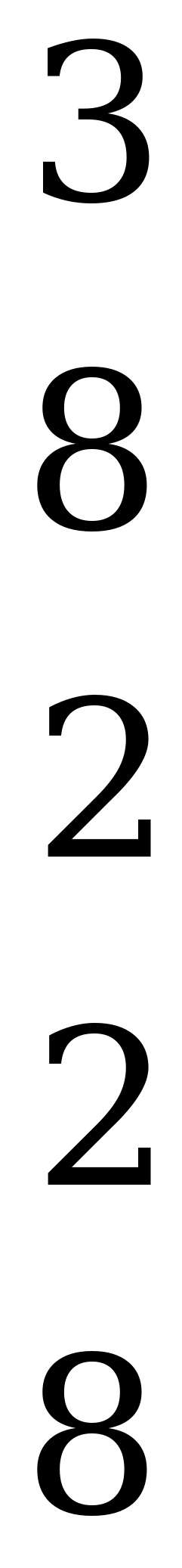
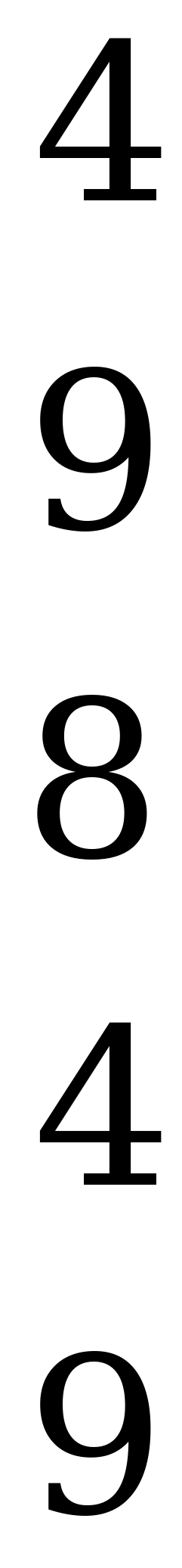

Стратегия 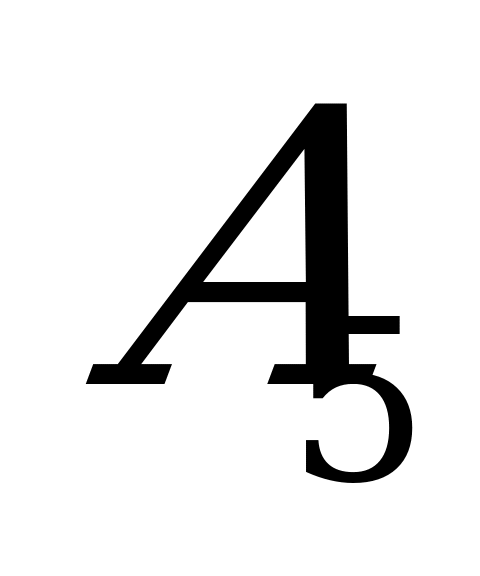 дублирует стратегию
дублирует стратегию 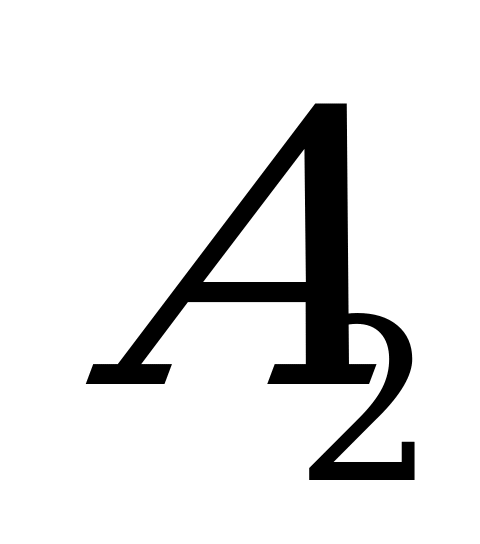 , поэтому любую из них можно отбросить. Отбрасывая
, поэтому любую из них можно отбросить. Отбрасывая 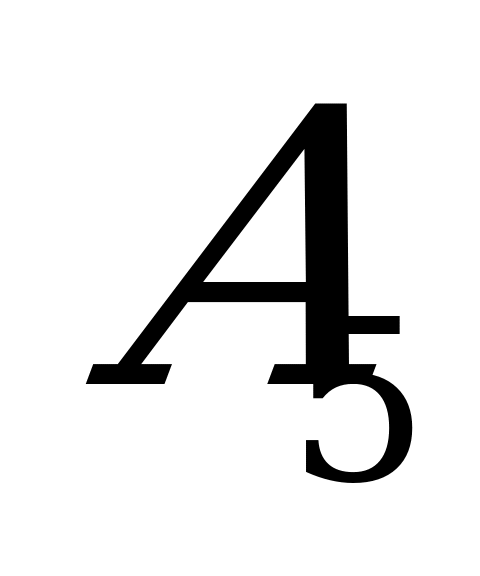 , замечаем, что в строке
, замечаем, что в строке  все выигрыши больше или равны соответствующим выигрышам строки
все выигрыши больше или равны соответствующим выигрышам строки  , значит
, значит  доминирует над
доминирует над  . Отбросим
. Отбросим  и получим матрицу 3×5:
и получим матрицу 3×5:




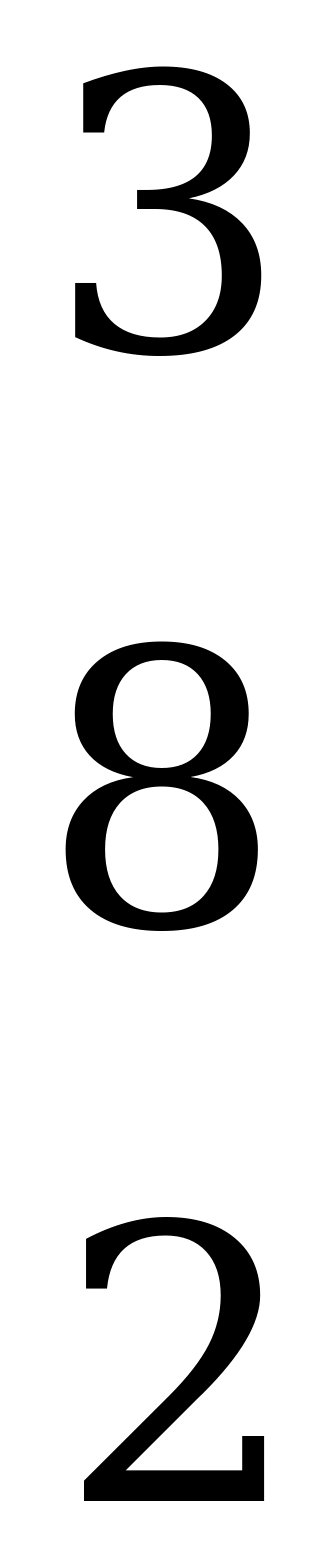

 .
.
Приглядевшись к последней матрице, замечаем, что в ней некоторые стратегии игрока B доминируют над другими: 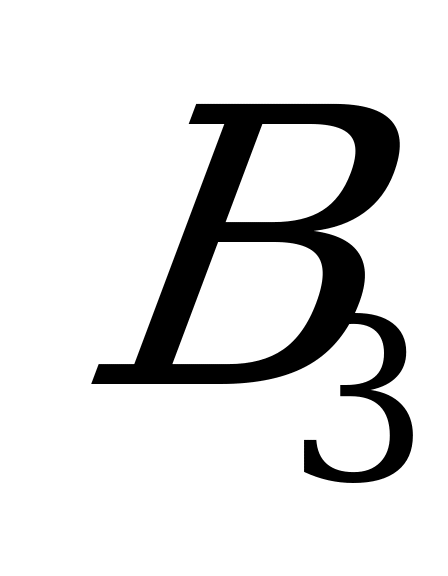 над
над  и
и 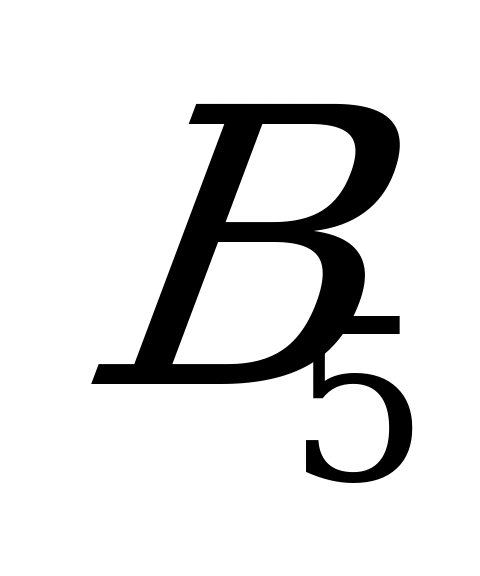 , а
, а 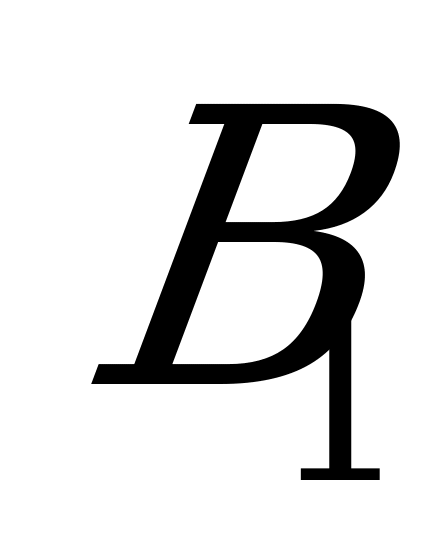 - над стратегией
- над стратегией 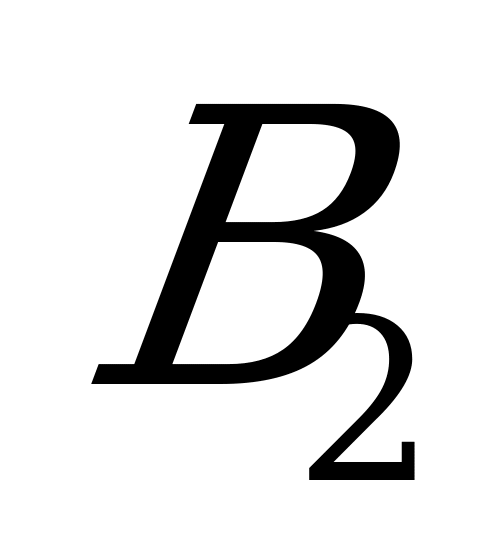 (игрок B стремится проиграть поменьше!). Отбрасывая столбцы
(игрок B стремится проиграть поменьше!). Отбрасывая столбцы 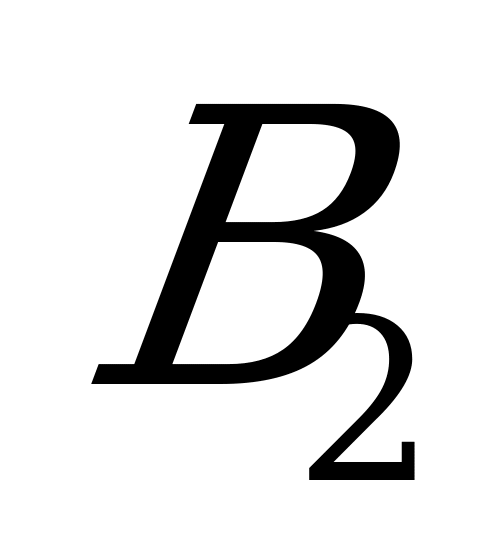 ,
,  ,
, 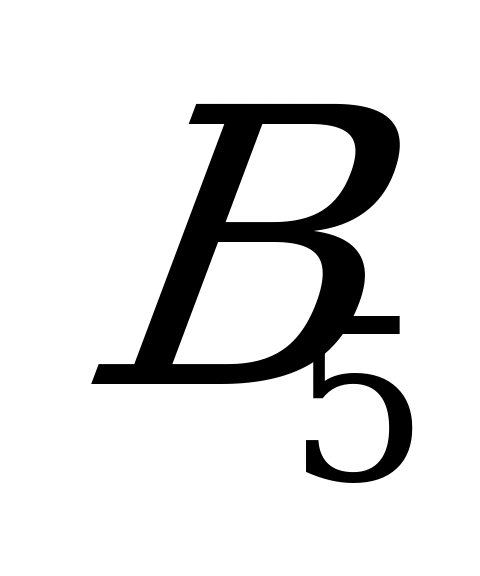 , получаем игру 3×2:
, получаем игру 3×2:



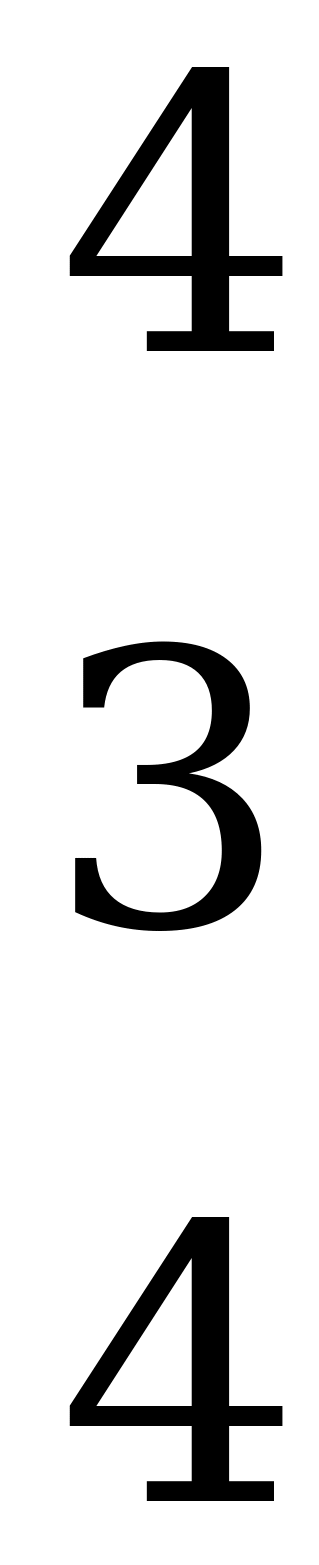
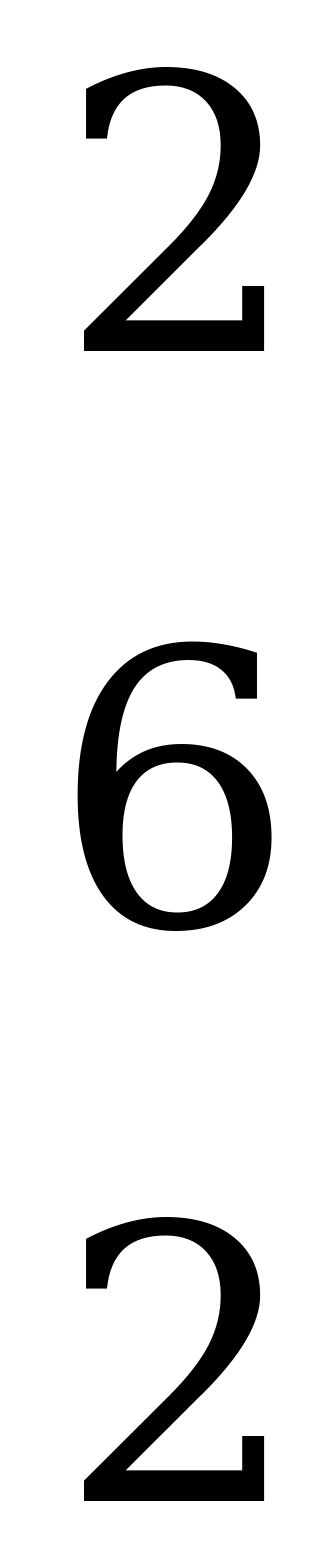
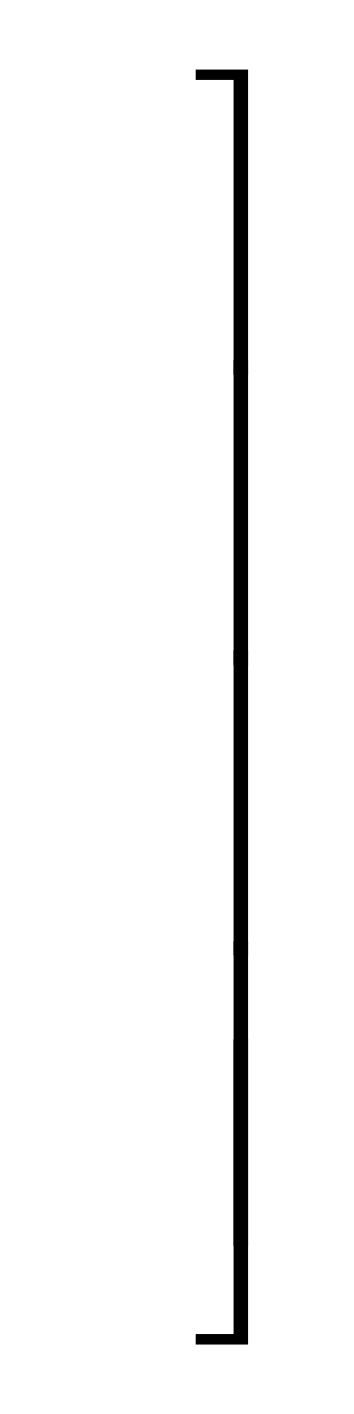 .
.
Стратегия  дублирует
дублирует  , поэтому её можно отбросить. Окончательно получим игру 2×2:
, поэтому её можно отбросить. Окончательно получим игру 2×2: 


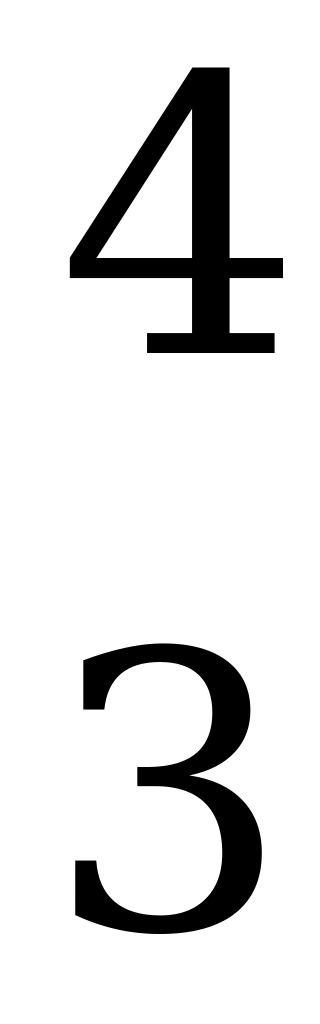

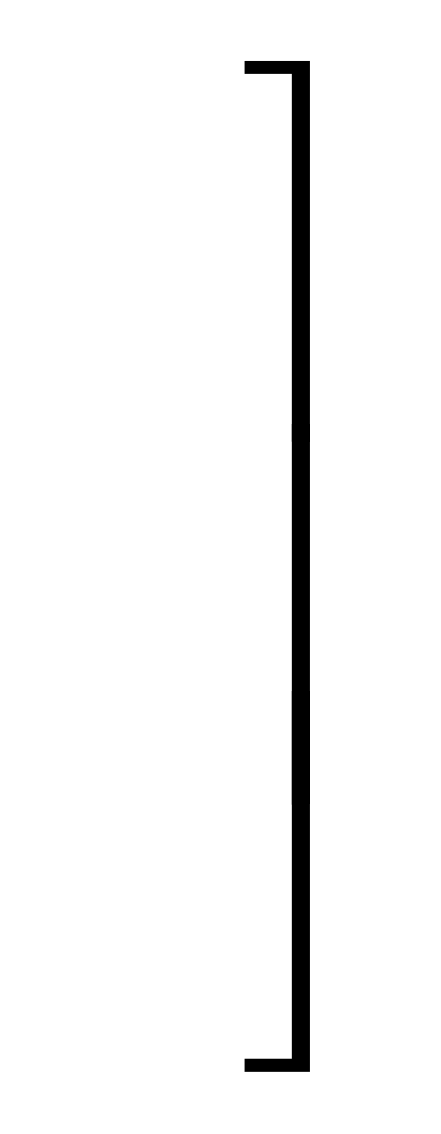 .
.
Можно сократить размер матрицы, разбив её на подматрицы, в которых суммы элементов по столбцам и строкам равны. Тогда вместо чистых стратегий в матрицу включаются смешанные. Элементы матрицы, соответствующие смешанным стратегиям, получаются делением соответствующих сумм элементов на число чистых стратегий, объединяемых в смешанную. Если смешанные стратегии входят в число оптимальных, то вероятности использования входящих в них чистых стратегий равны между собой.
Пример 5.
Рассмотрим матрицу, разбитую на четыре подматрицы, для которых выполняется условие равенства сумм элементов по строкам и столбцам:




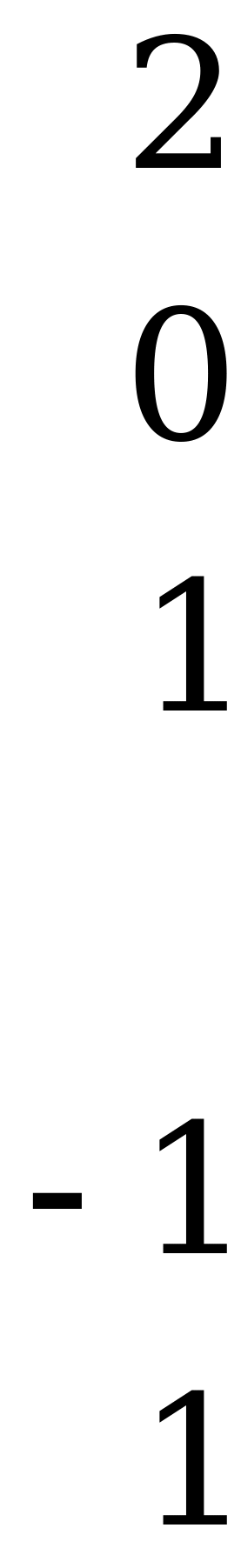



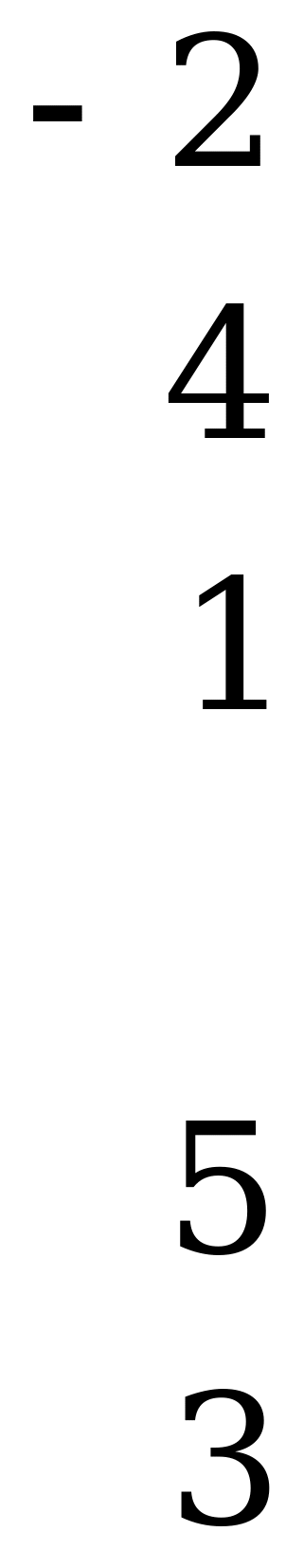
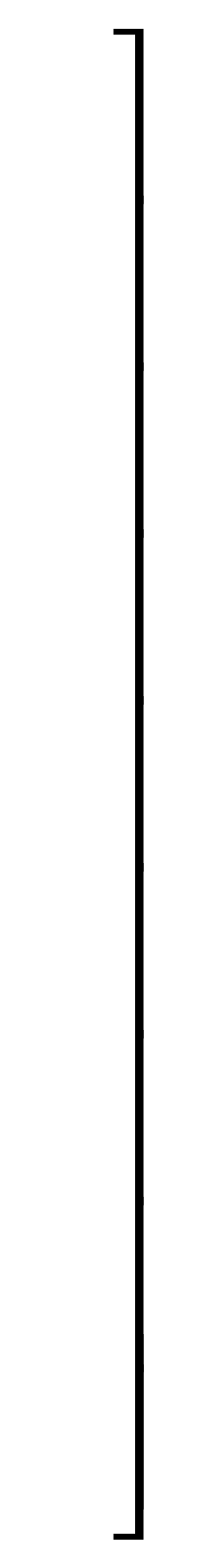 .
.
Объединяя стратегии  ,
,  и
и  ,
,  и
и  ,
, 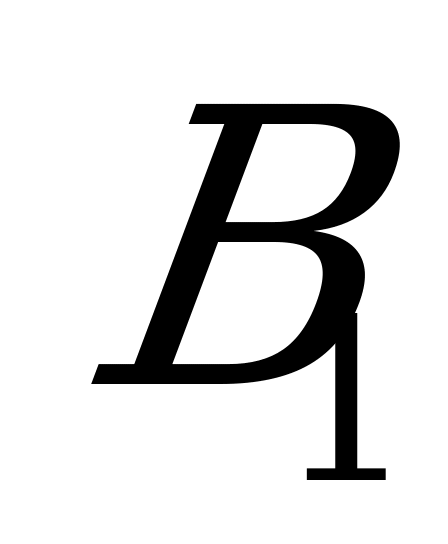 и
и 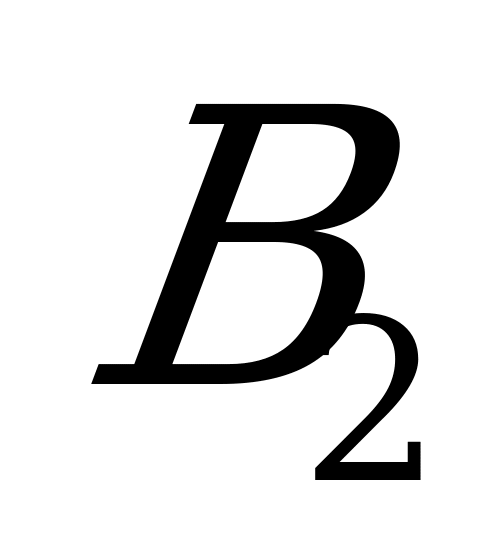 ,
,  и
и  , приводим матрицу к виду:
, приводим матрицу к виду: 





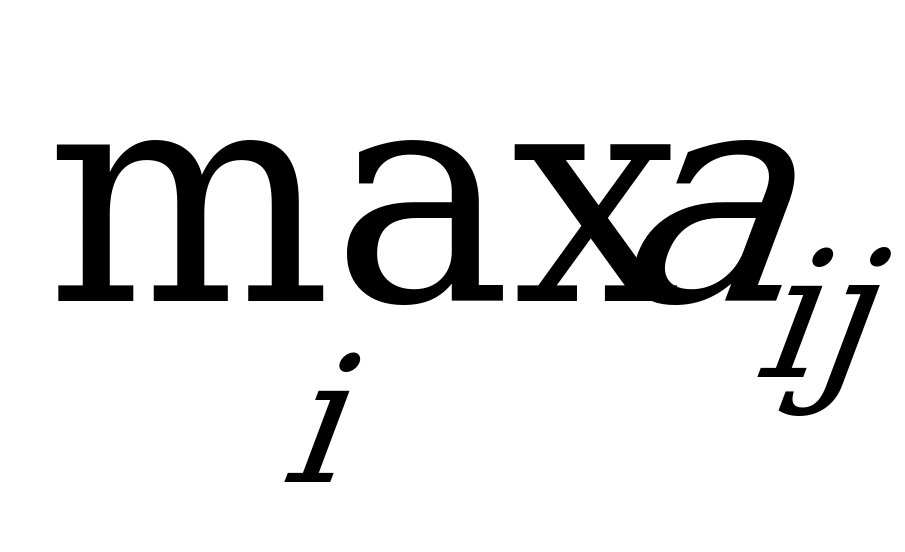
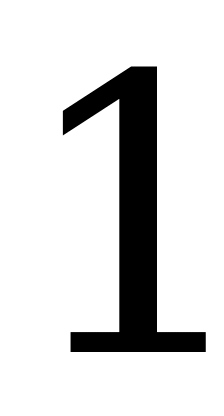


Полученная матрица содержит седловую точку. Поэтому решение игры, заданной последней матрицей, таково: 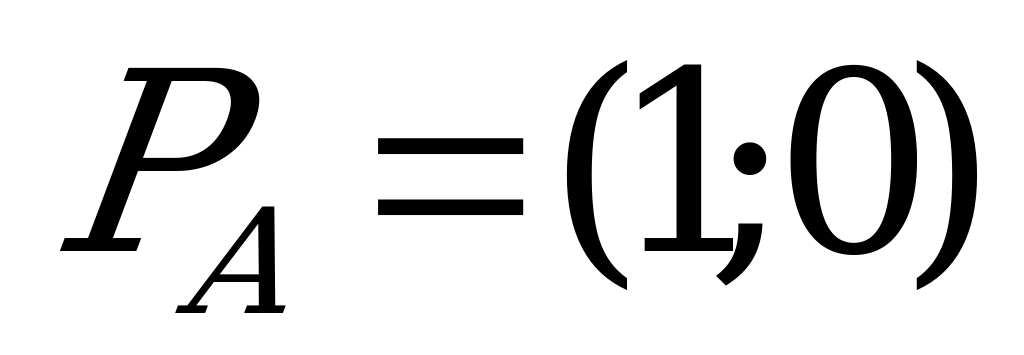 ,
, 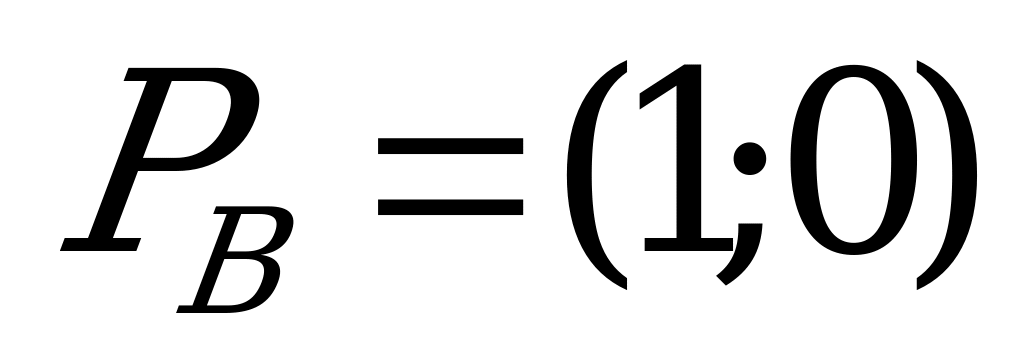 . Цена игры равна единице.
. Цена игры равна единице.
Это означает, что оптимальной для игрока A является комбинация стратегий  ,
,  и
и  , а для игрока B – комбинация стратегий
, а для игрока B – комбинация стратегий 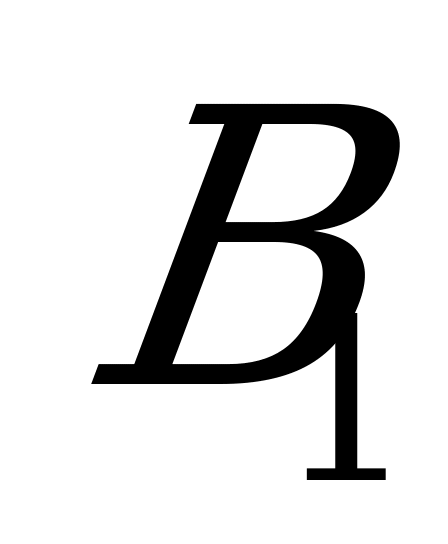 и
и 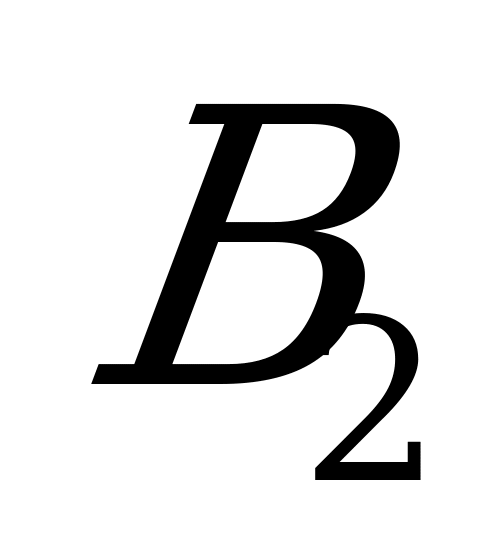 . Вероятности применения стратегий
. Вероятности применения стратегий  ,
,  и
и  равны между собой, сумма их равна 1, поэтому
равны между собой, сумма их равна 1, поэтому 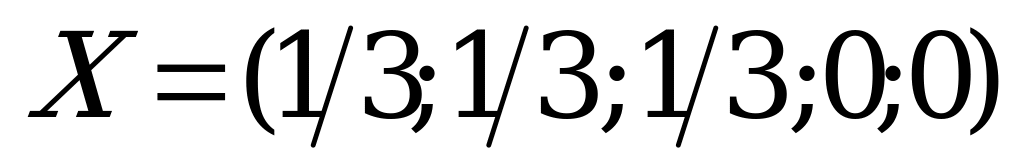 . Аналогично, оптимальная стратегия игрока B имеет вид:
. Аналогично, оптимальная стратегия игрока B имеет вид: 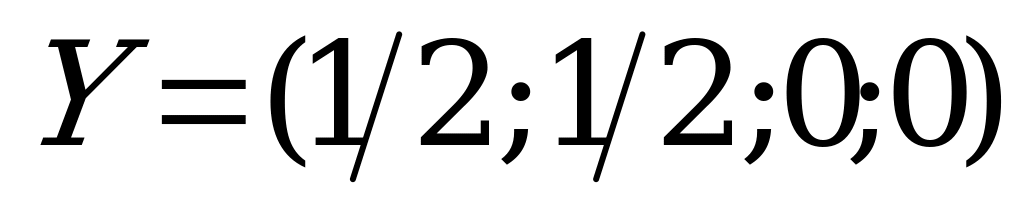 .
.
Таким образом, при решении игры m×n следует:
-
проверить, не содержит ли матрица седловой точки;
-
если седловой точки нет, то нужно сравнить между собой элементы строк и столбцов для исключения дублирующих и заведомо невыгодных стратегий;
-
рассмотреть возможность разбиения матрицы на подматрицы для замены некоторых групп чистых стратегий смешанными.
Аналитический метод для игр с платёжной матрицей второго порядка
Матрица игры имеет вид: 



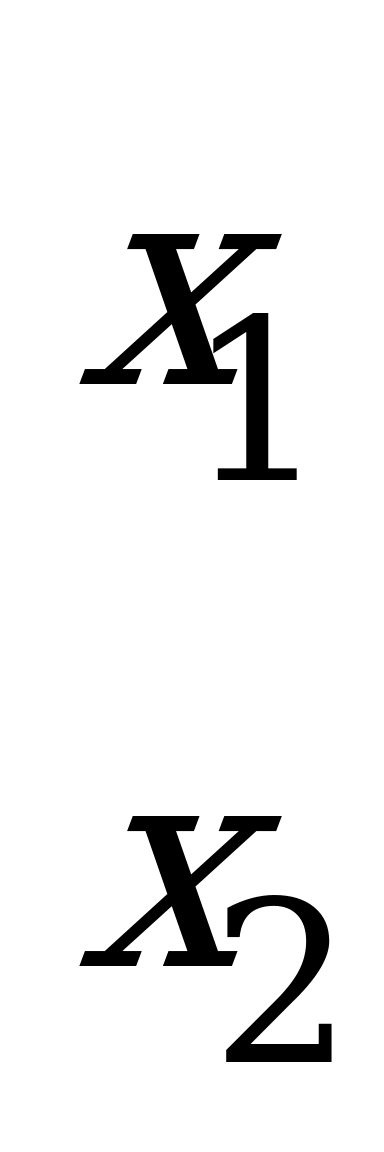

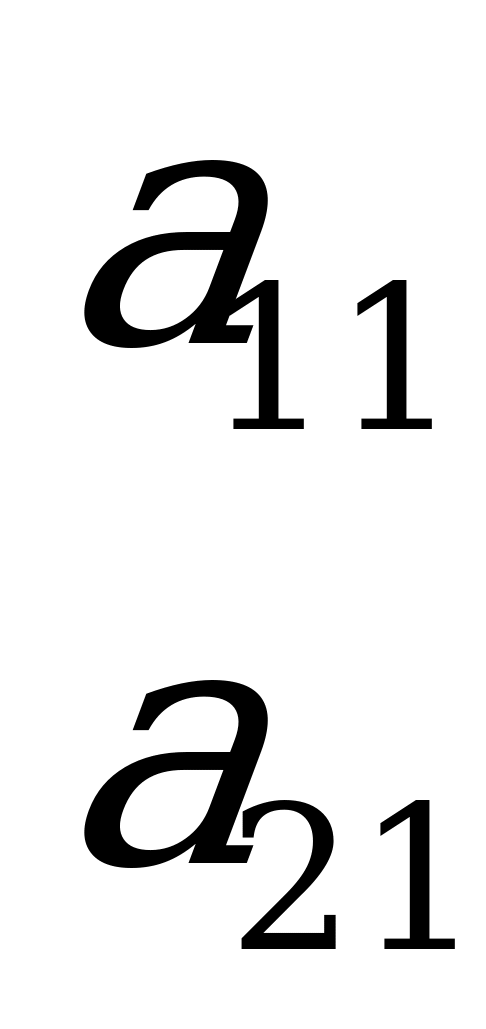
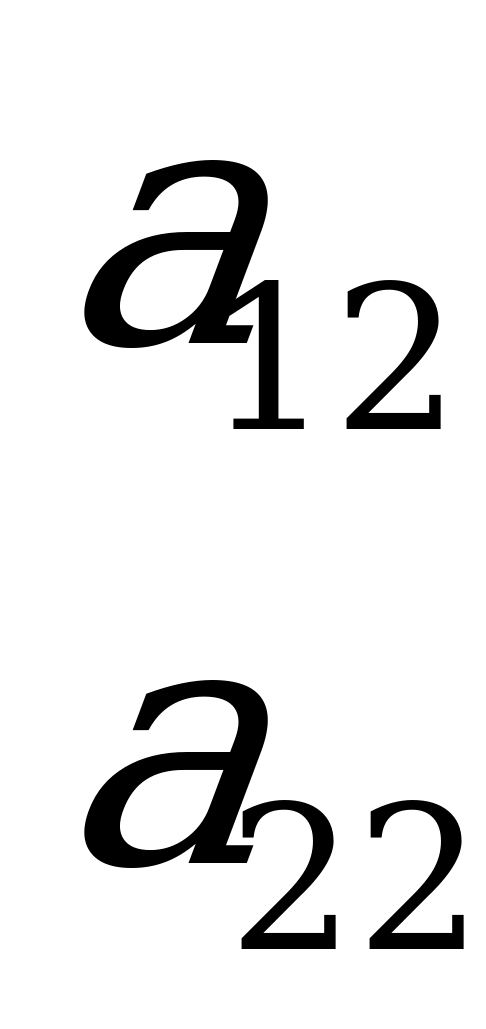
 .
.
Если седловой точки нет, то решением игры являются смешанные стратегии  ,
,  .
.
Согласно основной теореме теории игр, применение оптимальной стратегии 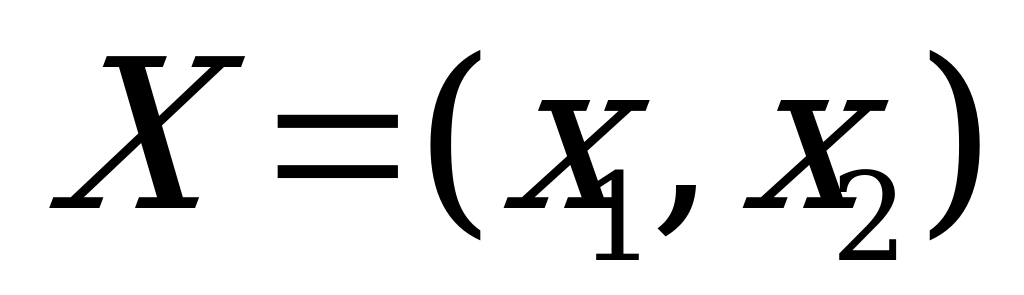 обеспечивает для игрока
обеспечивает для игрока  получение выигрыша, равного цене игры
получение выигрыша, равного цене игры  , независимо от действий игрока
, независимо от действий игрока  . Таким образом,
. Таким образом,
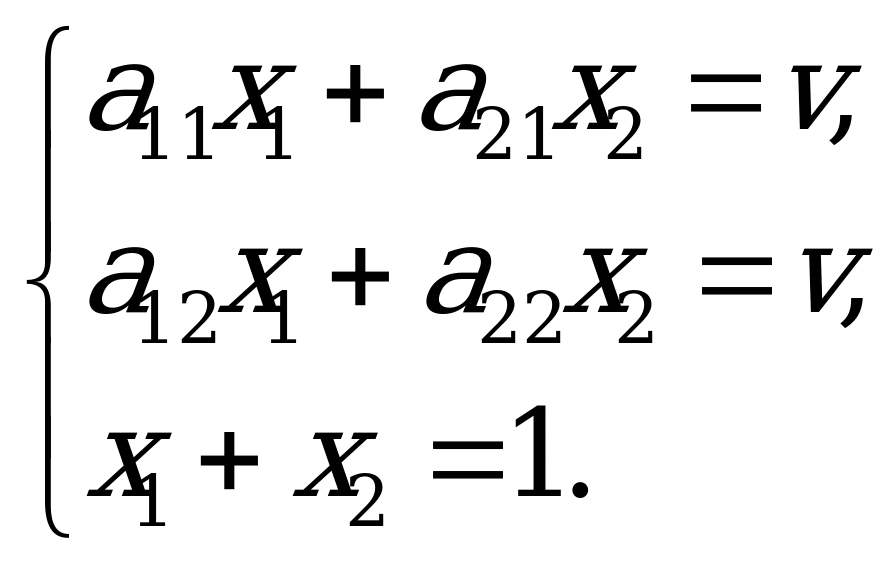
Из первого уравнения системы вычтем второе, а из третьего уравнения выразим 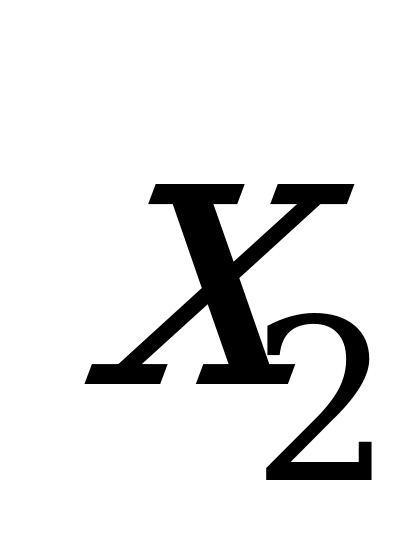 :
:
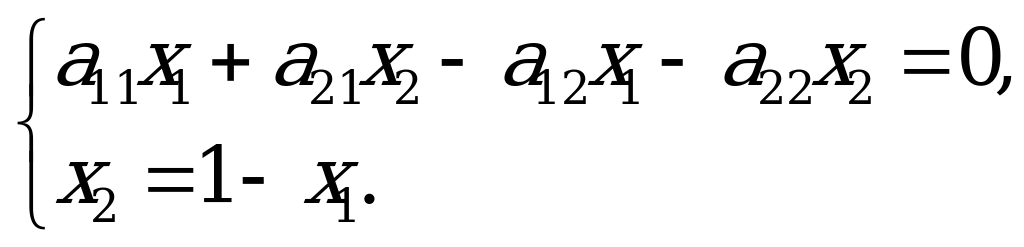
В первое уравнение подставим полученное выражение для 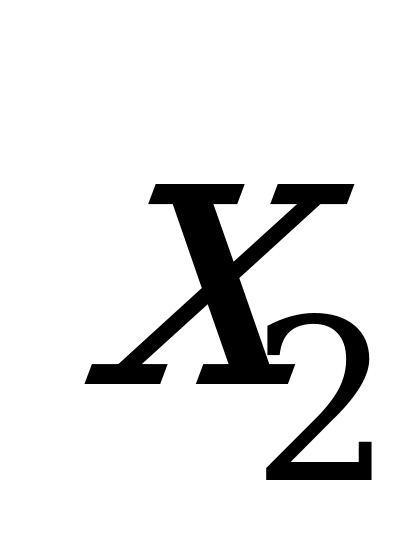 и определим
и определим  :
:
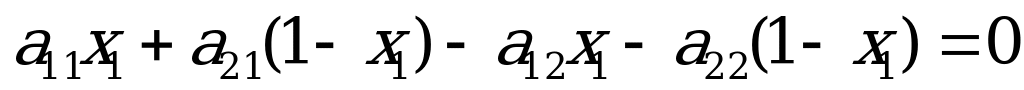 ;
;
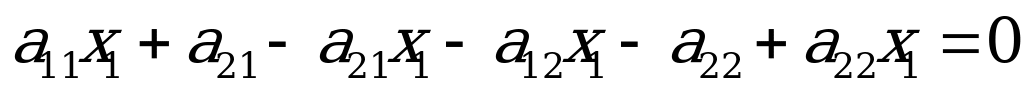 ;
;
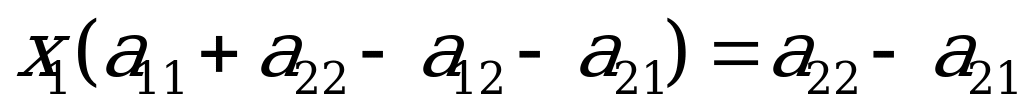 ;
;

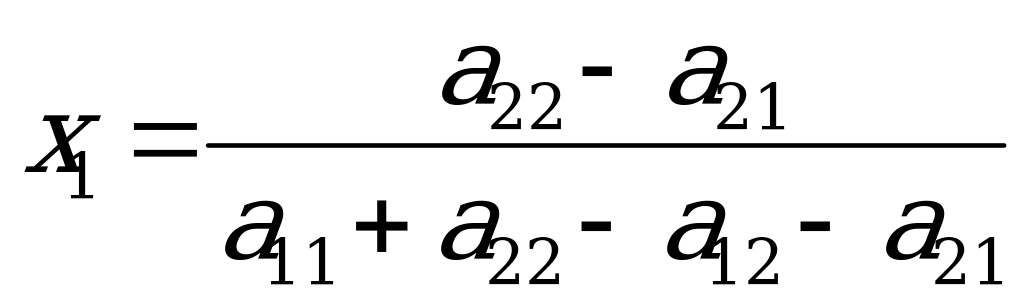 . (1)
. (1)
Т огда
огда 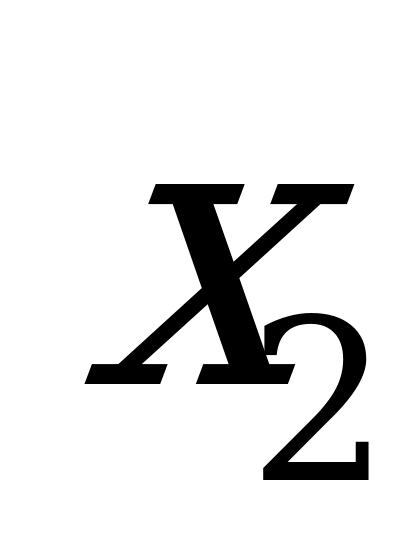 равно:
равно: 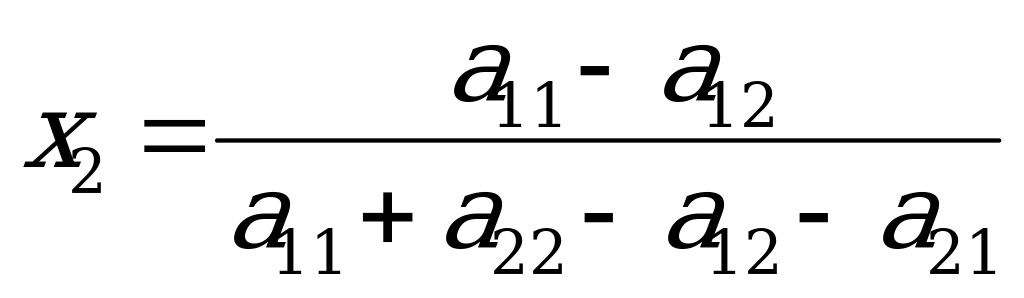 . (2)
. (2)
Подставляя значения  и
и 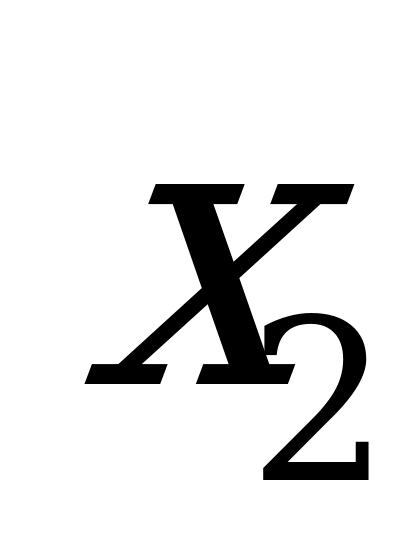 в одно из уравнений первоначальной системы, получаем:
в одно из уравнений первоначальной системы, получаем:

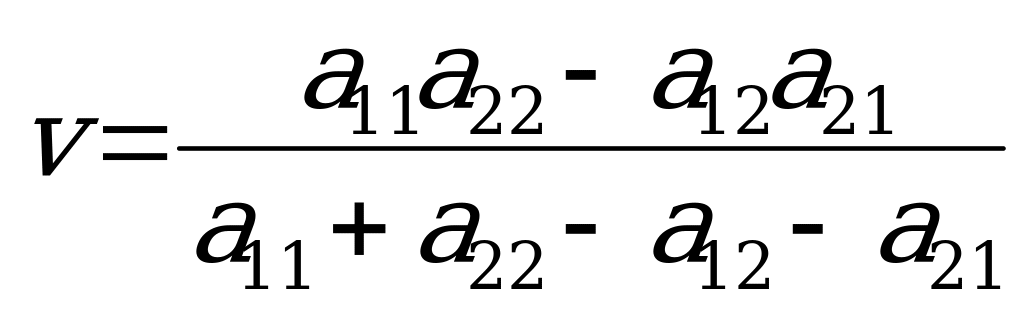 . (3)
. (3)
Аналогично, если игрок  придерживается своей оптимальной стратегии
придерживается своей оптимальной стратегии 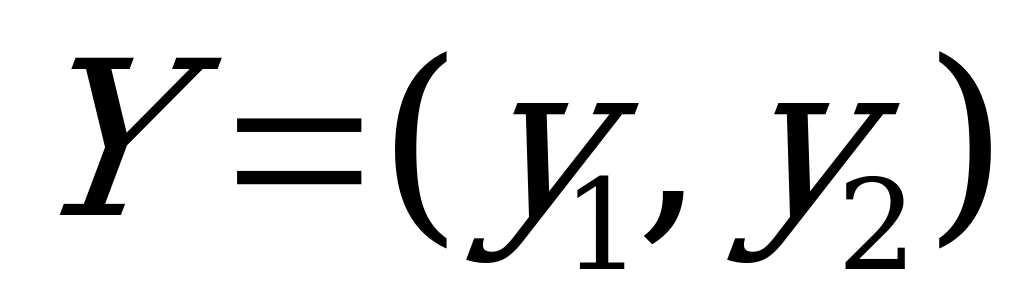 , то его проигрыш остаётся неизменным и равным цене игры
, то его проигрыш остаётся неизменным и равным цене игры  независимо от действий игрока
независимо от действий игрока  . Таким образом,
. Таким образом,
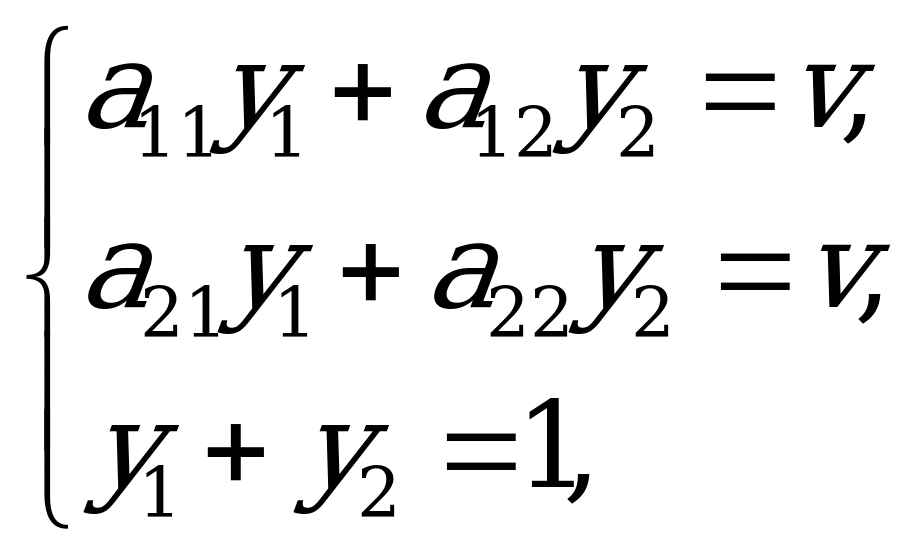
о
 ткуда
ткуда 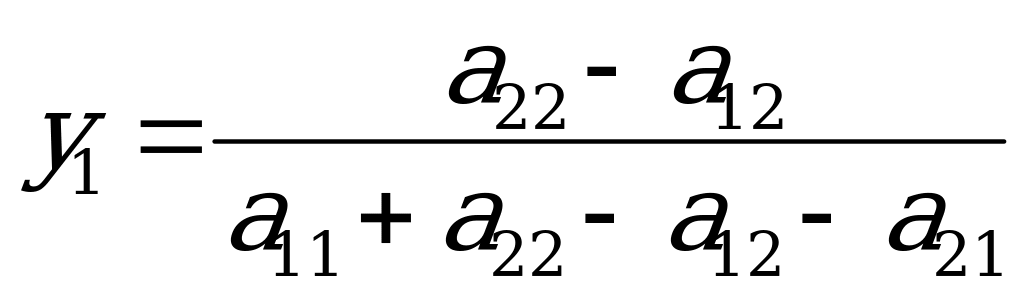 ,
, 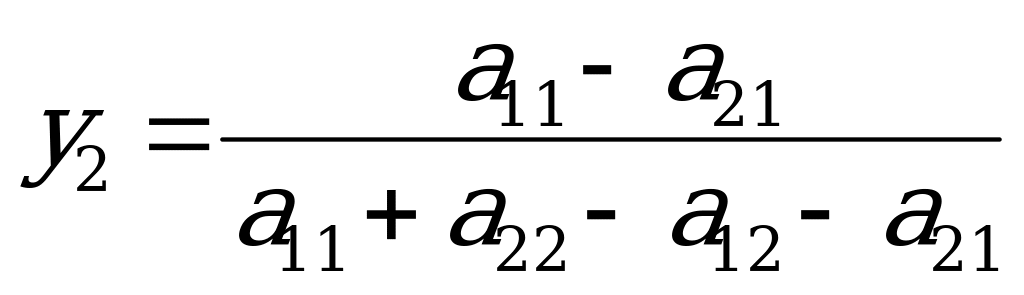 . (4)
. (4)
Пример 6.
Найти решение игры, заданной матрицей 



 .
.
Решение. Имеем 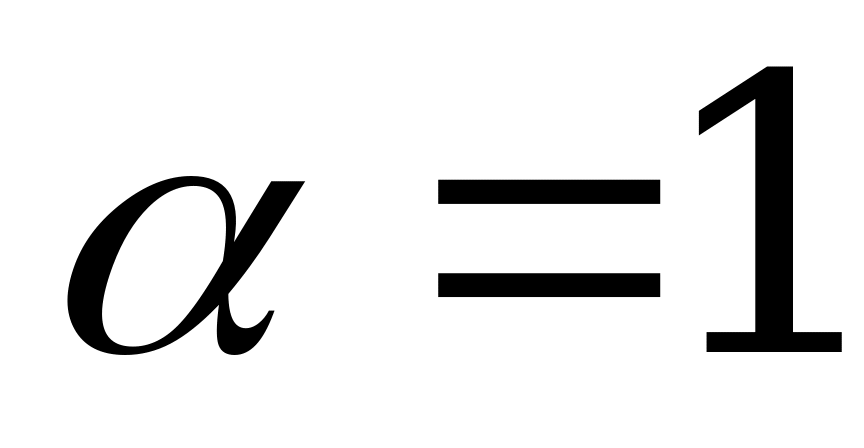 ,
, 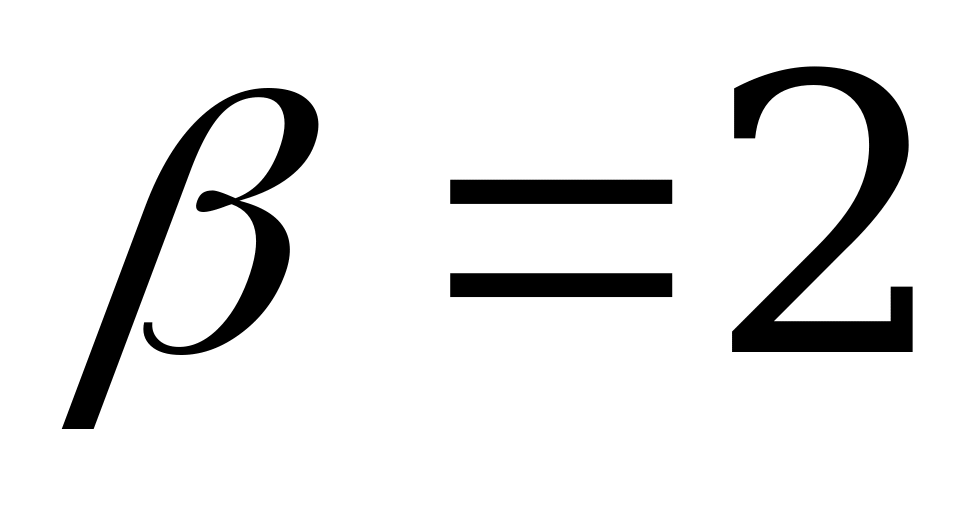 ; матрица не имеет седловой точки. Находим оптимальные стратегии и цену игры:
; матрица не имеет седловой точки. Находим оптимальные стратегии и цену игры: 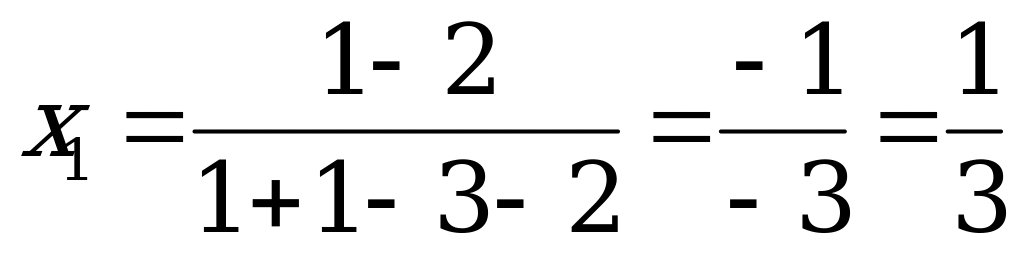 ,
, 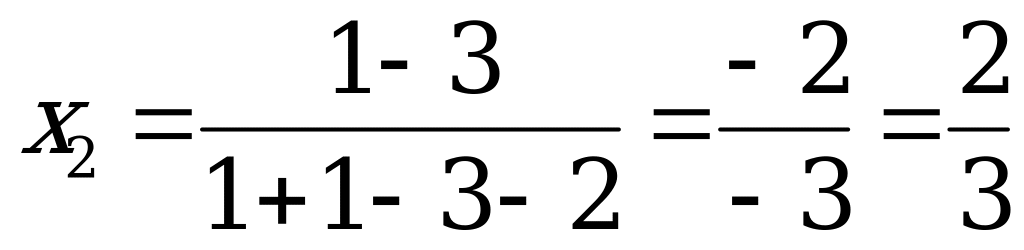 ;
;
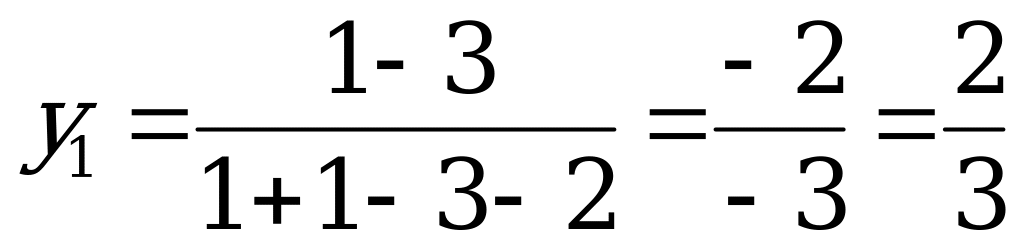 ,
, 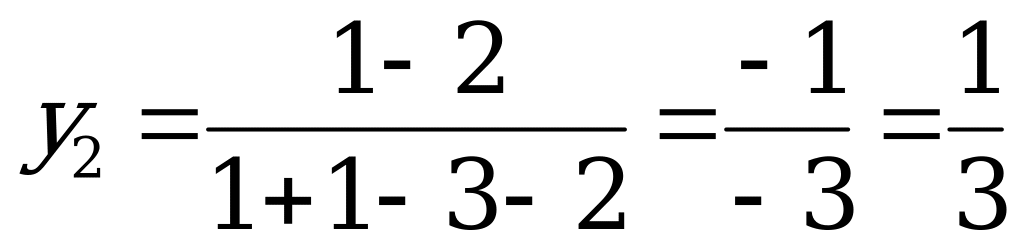 ;
;
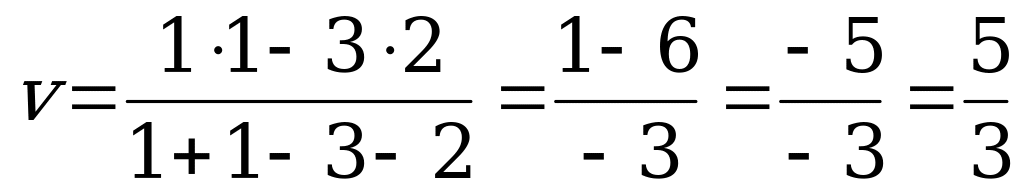 .
.
Ответ. 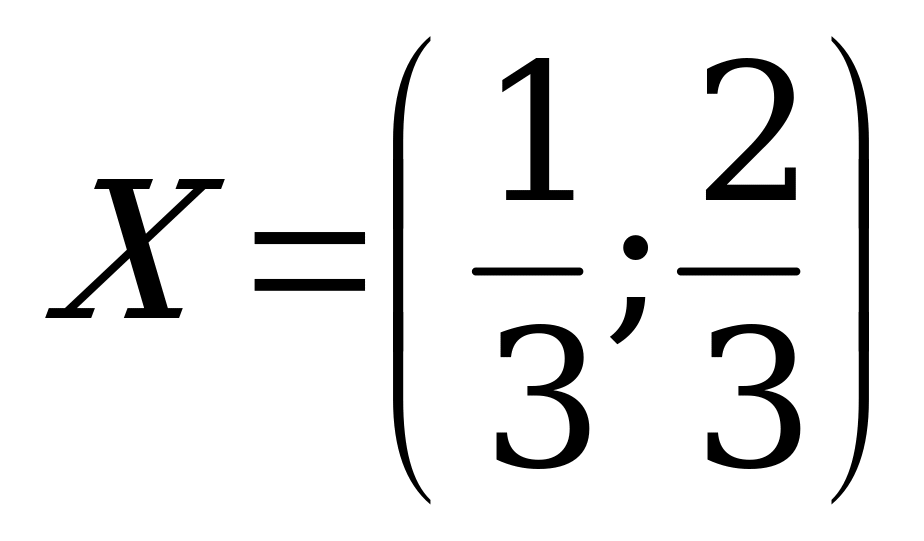 ,
, 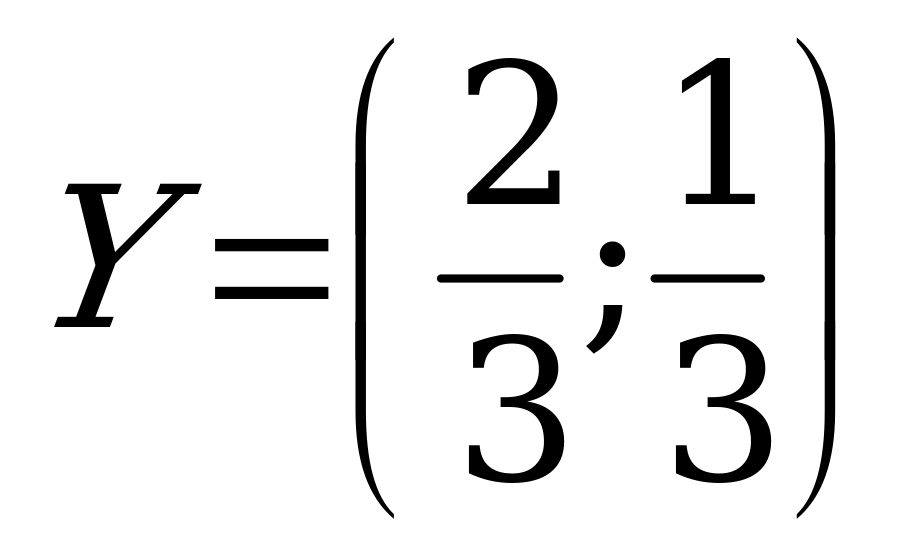 ,
, 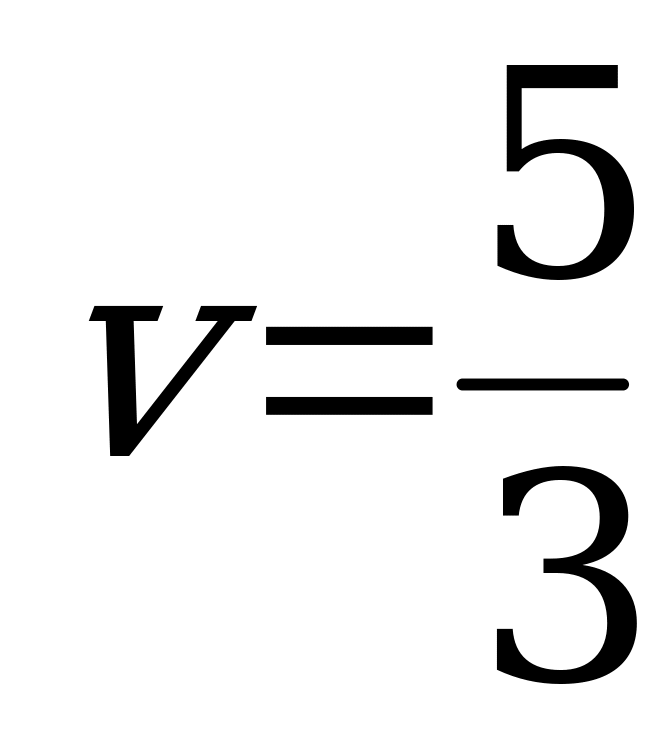 .
.
Графический метод
Этот метод можно использовать, когда у одного из игроков в распоряжении лишь две чистые стратегии. Задача легко решается путём построения прямых, соответствующих ожидаемым выигрышам одного игрока при различных чистых стратегиях другого игрока.
Пример 7.
Рассмотрим игру двух участников с нулевой суммой и платёжной матрицей



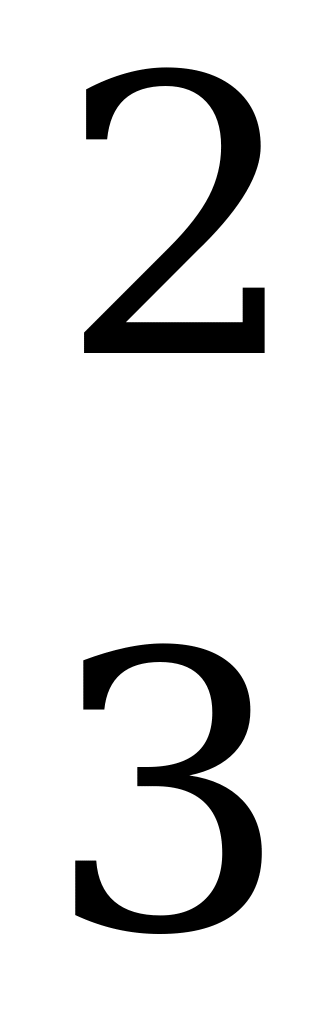


 .
.
Нижняя цена этой игры 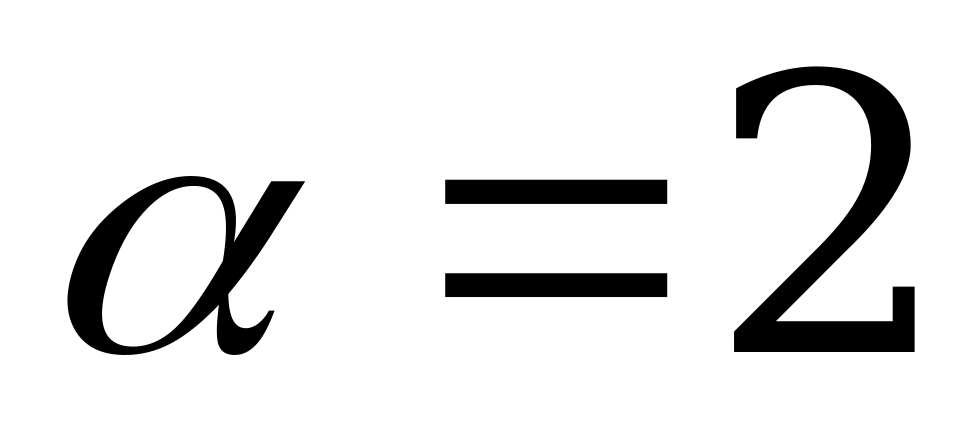 отличается от её верхней цены
отличается от её верхней цены 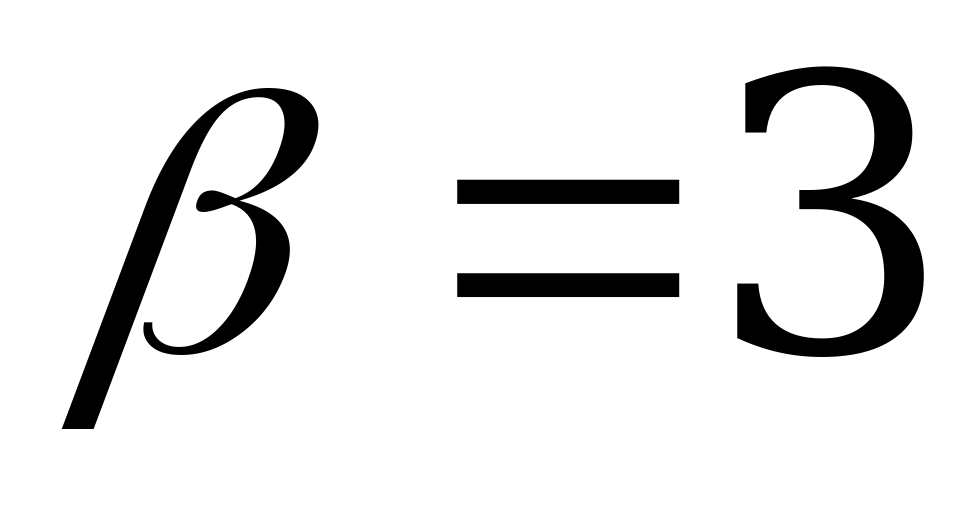 , то есть игра не имеет седловой точки.
, то есть игра не имеет седловой точки.
Р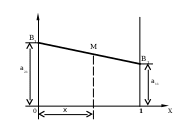 ешение игры можно найти с помощью следующих построений.
ешение игры можно найти с помощью следующих построений.
На оси абсцисс отложим отрезок, длина которого равна единице. Правый конец отрезка (точка 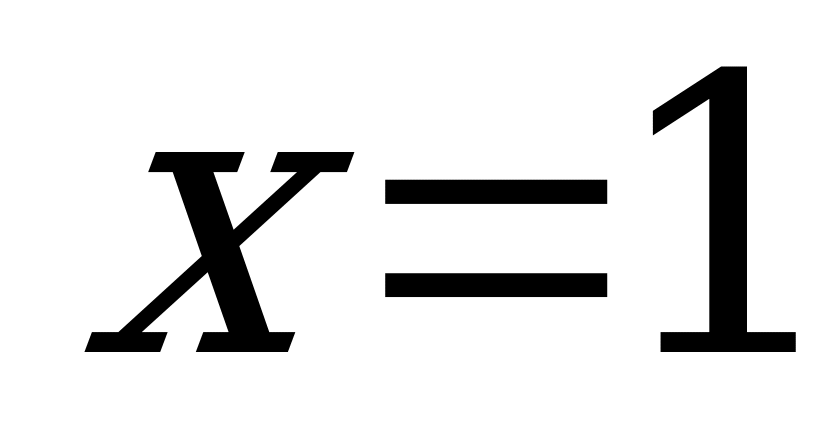 ) соответствует стратегии
) соответствует стратегии  , левый – стратегии
, левый – стратегии 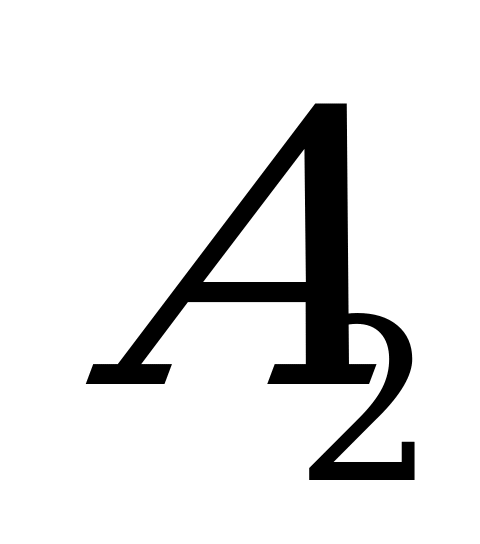 . Промежуточные точки
. Промежуточные точки 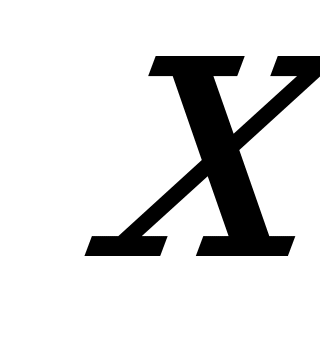 соответствуют некоторым смешанным стратегиям (
соответствуют некоторым смешанным стратегиям (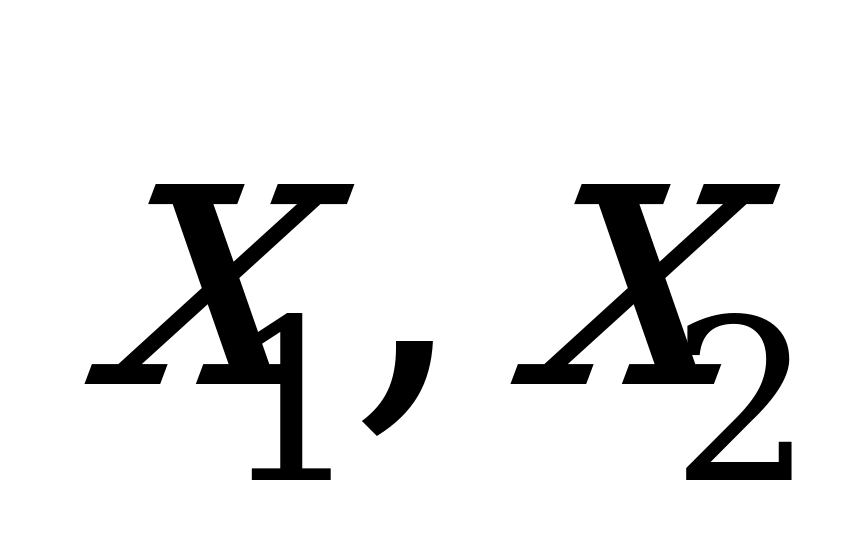 ), где
), где  ,
,  . На концах отрезка проведём прямые, перпендикулярные оси абсцисс, на них будем откладывать выигрыш при соответствующих чистых стратегиях. Если игрок
. На концах отрезка проведём прямые, перпендикулярные оси абсцисс, на них будем откладывать выигрыш при соответствующих чистых стратегиях. Если игрок  применяет стратегию
применяет стратегию  , то выигрыш при использовании чистых стратегий
, то выигрыш при использовании чистых стратегий  и
и  составляет, соответственно,
составляет, соответственно, 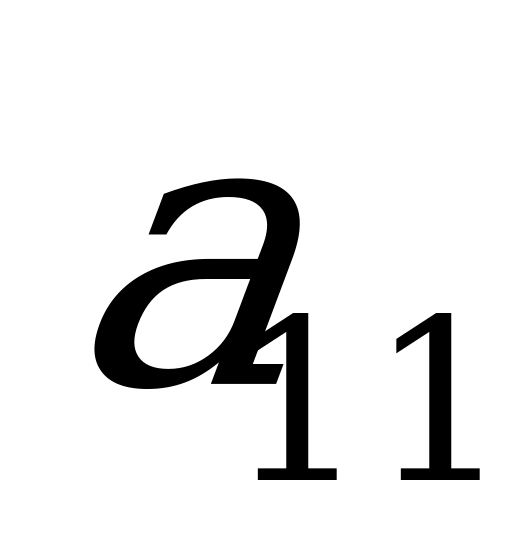 и
и 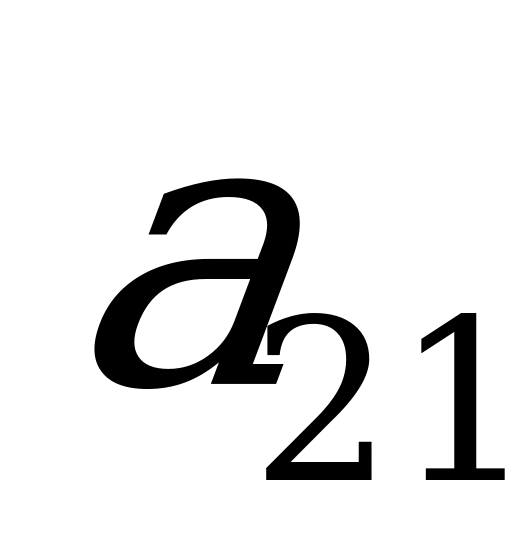 .
.
Отложим эти точки на прямых и соединим полученные точки прямой 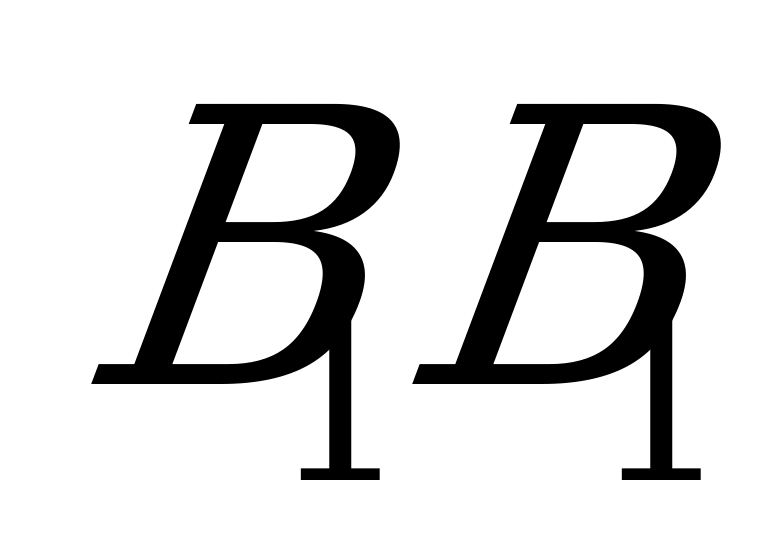 . Если игрок
. Если игрок  применяет смешанную стратегию, то его выигрышу соответствует некоторая точка
применяет смешанную стратегию, то его выигрышу соответствует некоторая точка 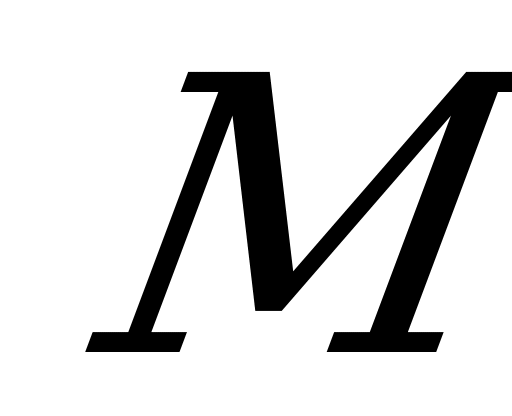 , лежащая на этой прямой.
, лежащая на этой прямой.
А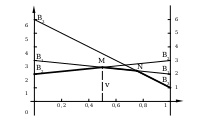 налогично можно построить прямые
налогично можно построить прямые 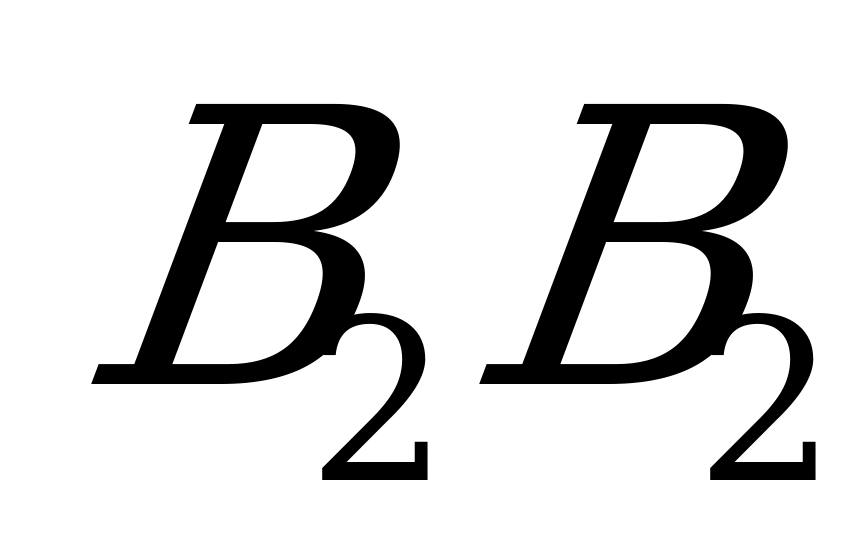 и
и 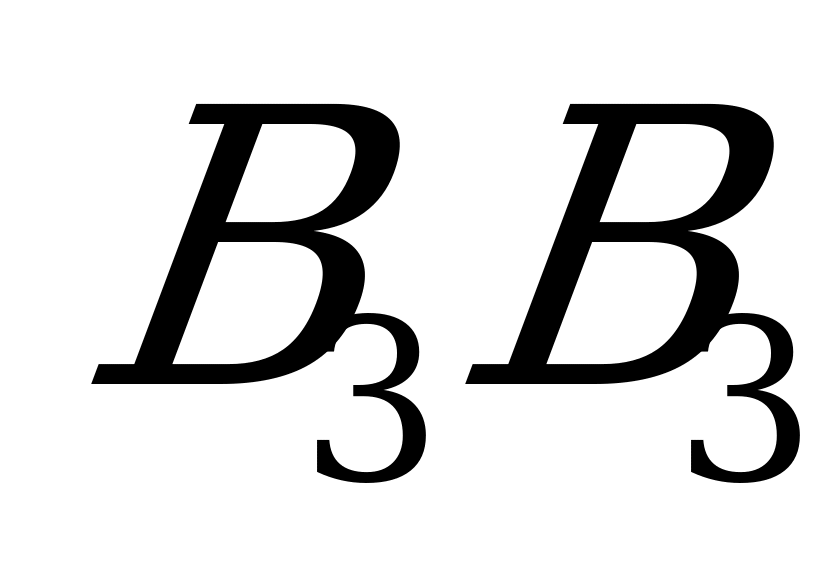 , соответствующие стратегиям
, соответствующие стратегиям 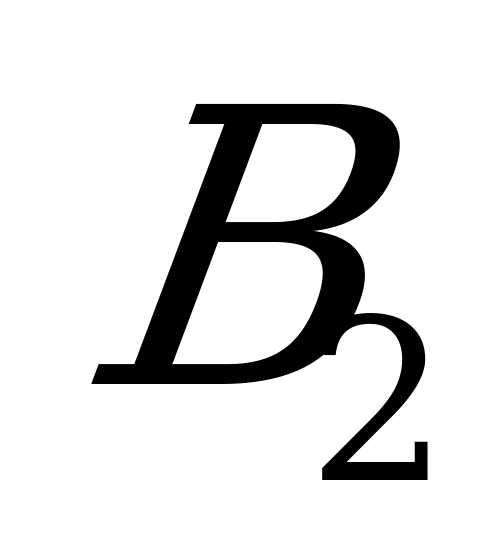 и
и 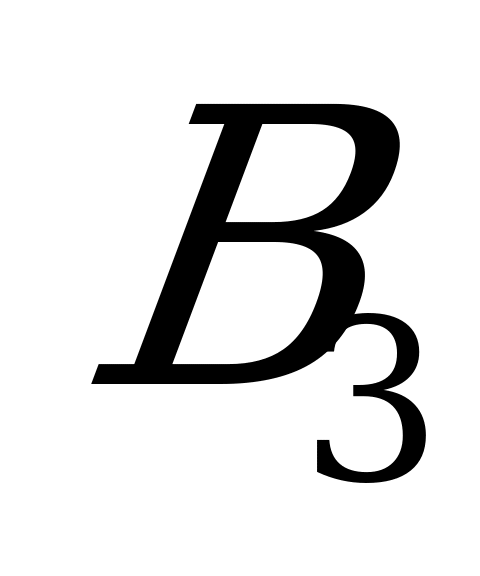 игрока
игрока  .
.
Выделенная ломаная линия 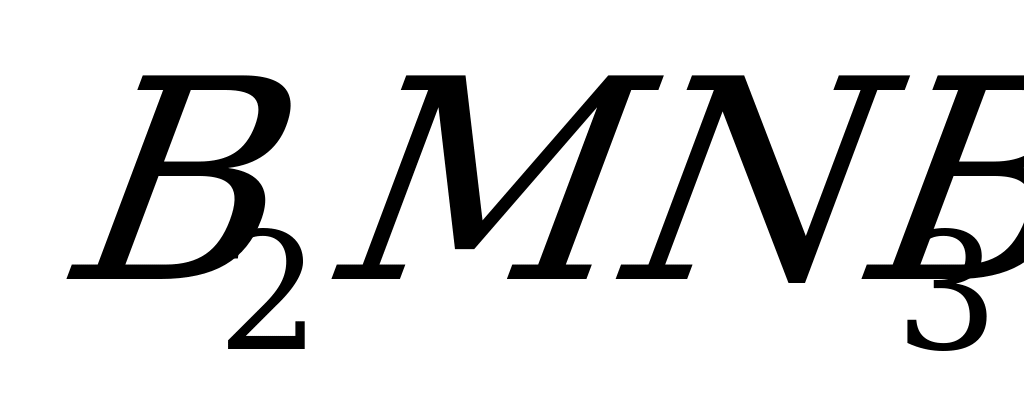 определяет минимальный гарантированный выигрыш первого игрока независимо от действий второго игрока.
определяет минимальный гарантированный выигрыш первого игрока независимо от действий второго игрока.
Точка 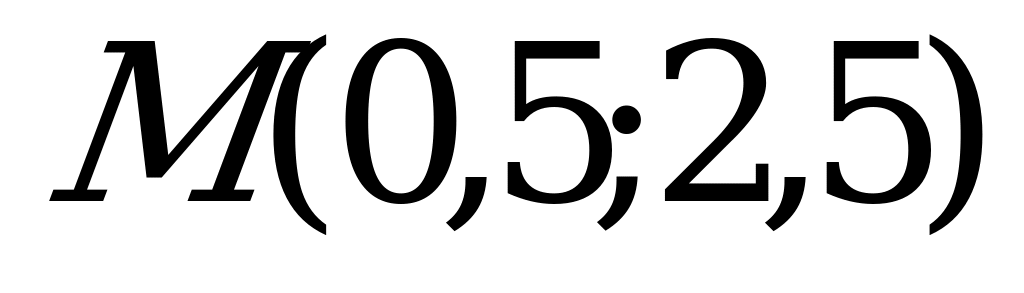 , в которой он максимален, определяет цену игры и её решение. Таким образом,
, в которой он максимален, определяет цену игры и её решение. Таким образом, 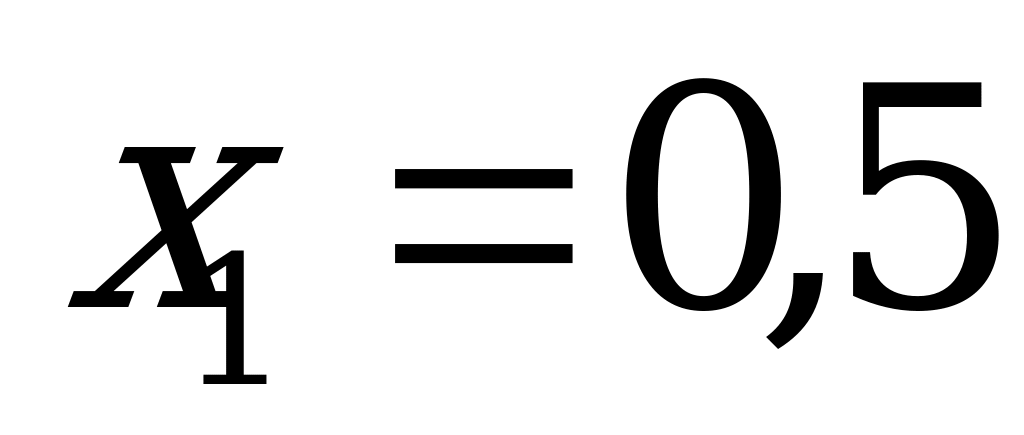 ;
; 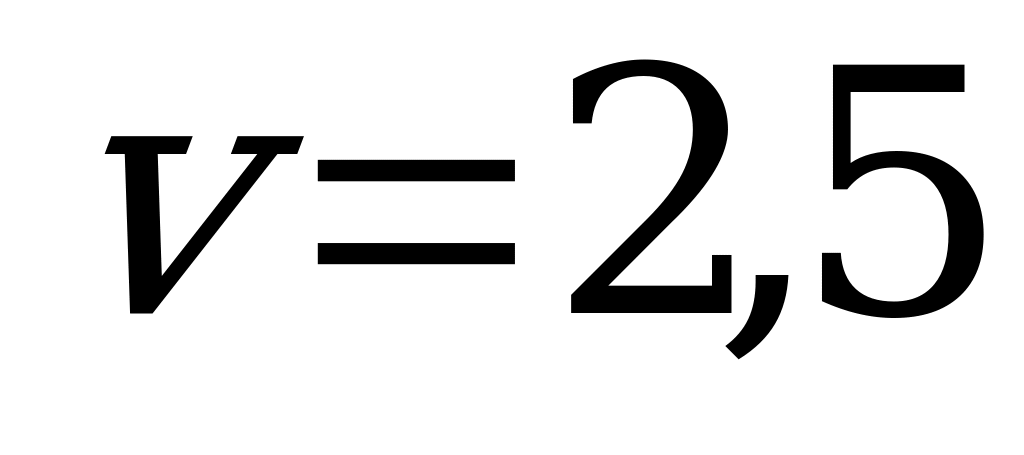 . А так как первый игрок располагает лишь двумя стратегиями и
. А так как первый игрок располагает лишь двумя стратегиями и 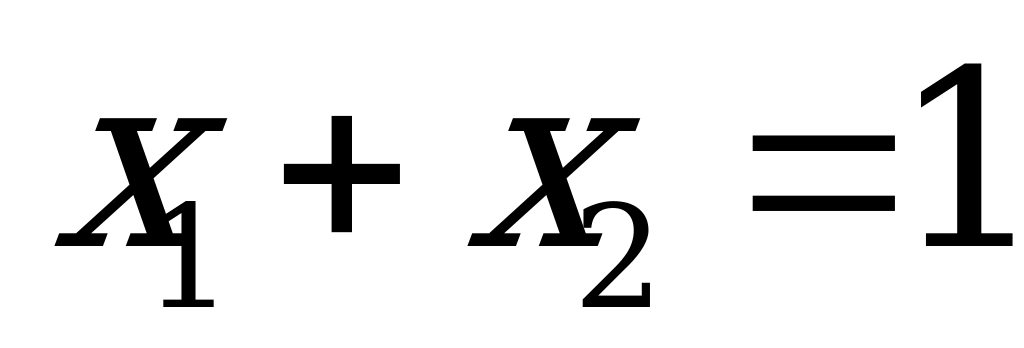 , то его оптимальная смешанная стратегия
, то его оптимальная смешанная стратегия 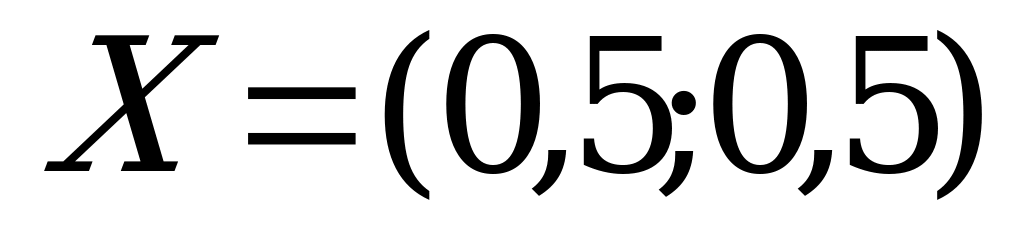 .
.
Следует отметить, что геометрические построения используются для определения активных стратегий игроков. Затем решение игры можно получить с помощью формул (1)–(4). Формулы (1)–(4) можно использовать, так как из соответствующей матрицы исключаются все стратегии, кроме активных, и она содержит две строки и два столбца.
Пример 8. 
Найти решение игры, заданной матрицей 

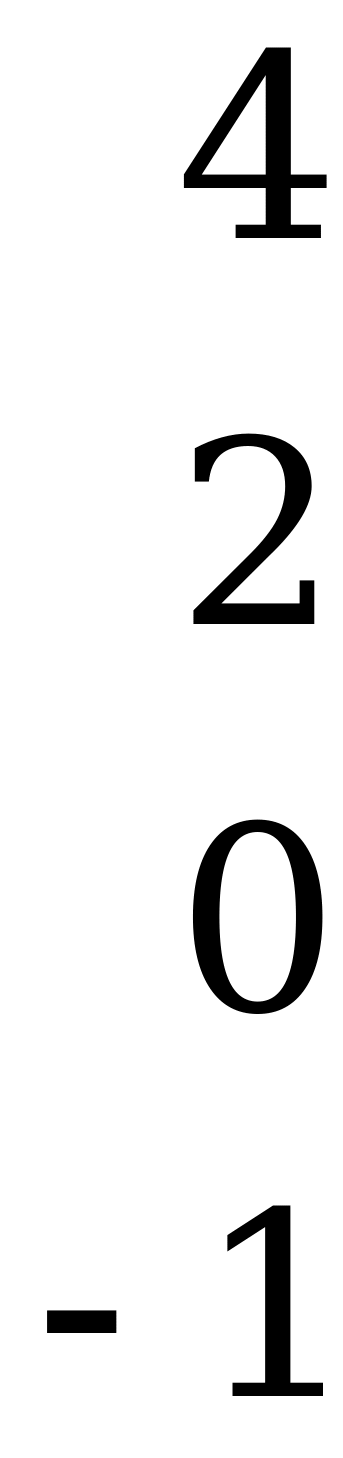

 .
.
Р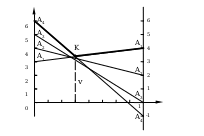 ешение. Матрица имеет размерность 4×2, поэтому решение задачи находим для игрока
ешение. Матрица имеет размерность 4×2, поэтому решение задачи находим для игрока  . На рисунке построены прямые, соответствующие стратегиям игрока
. На рисунке построены прямые, соответствующие стратегиям игрока  .
.
Жирной линией изображена ломаная 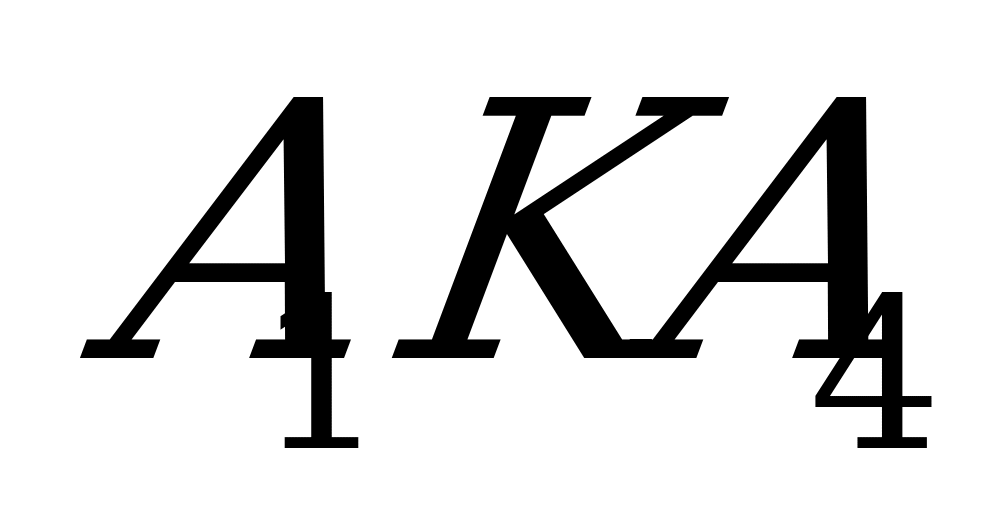 , определяющая максимальный проигрыш игрока
, определяющая максимальный проигрыш игрока  . Точка
. Точка 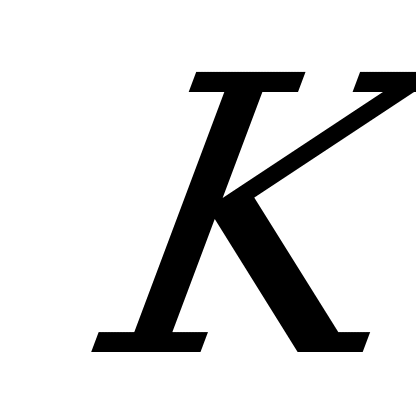 , в которой он минимален, определяет цену игры. Таким образом,
, в которой он минимален, определяет цену игры. Таким образом, 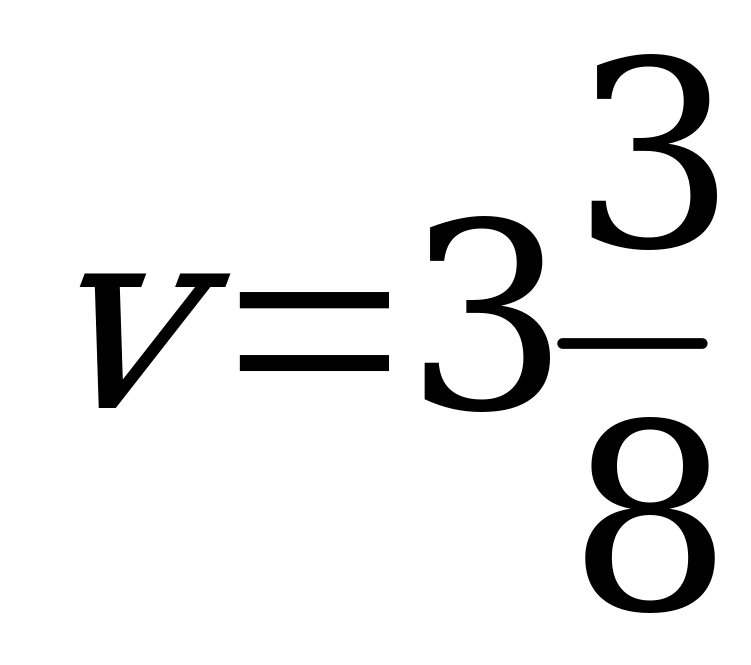 ,
, 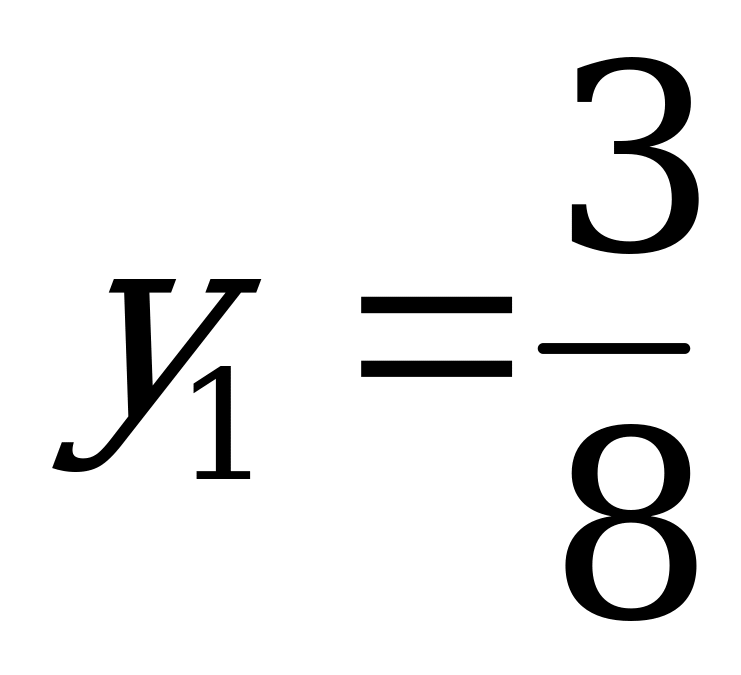 . Активными стратегиями игрока
. Активными стратегиями игрока  являются первая и четвёртая:
являются первая и четвёртая:




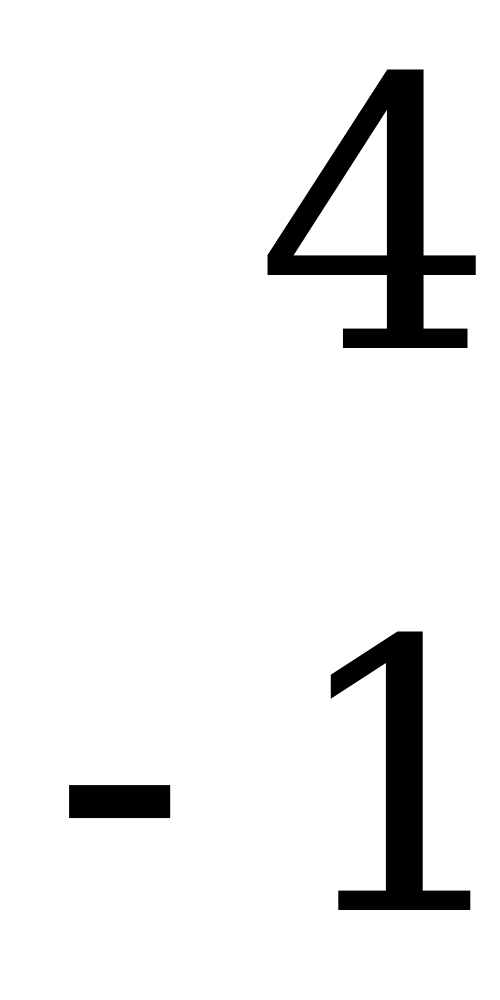

 .
.
Используя аналитический метод для игр с платёжной матрицей второго порядка, получаем 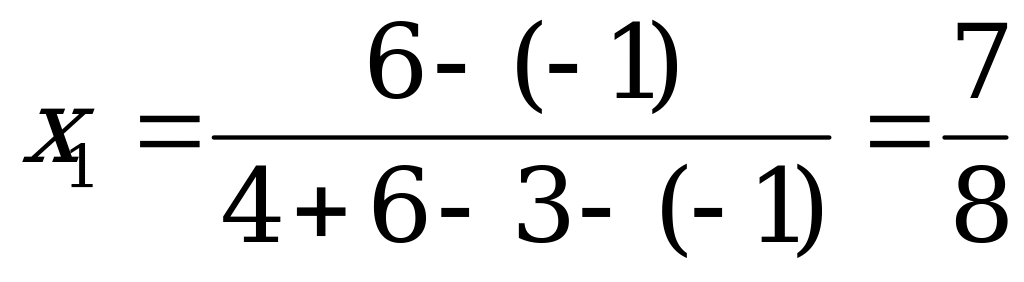 ,
, 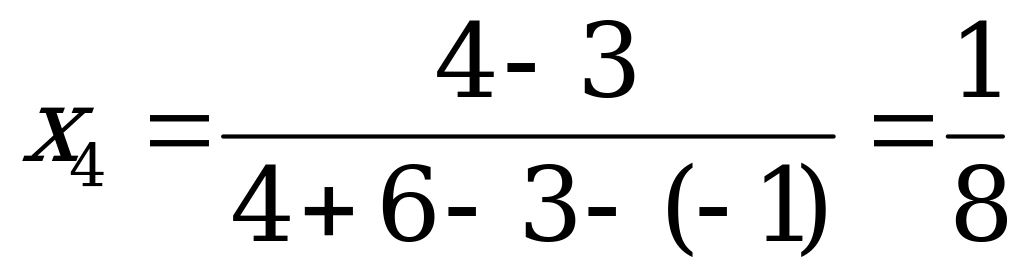 .
.
Решение игры таково: 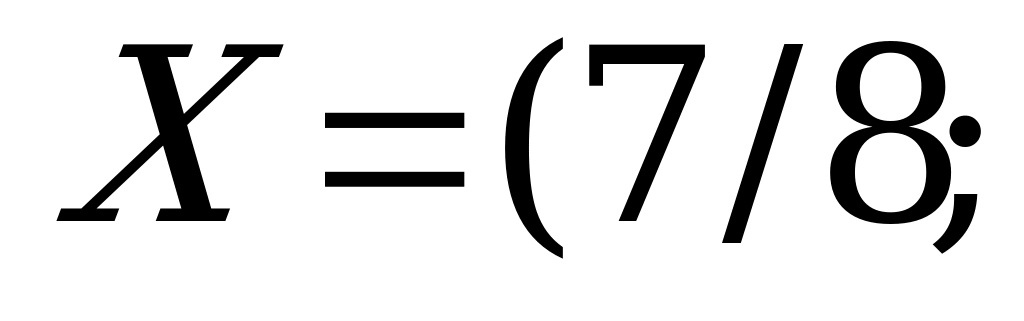
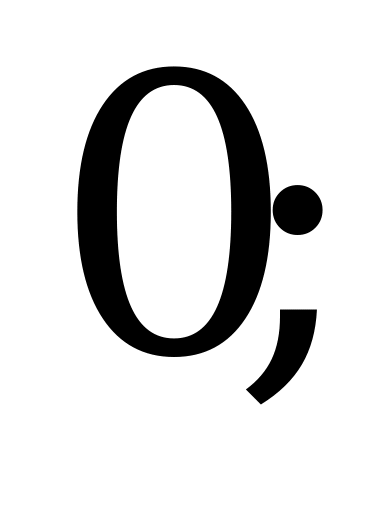
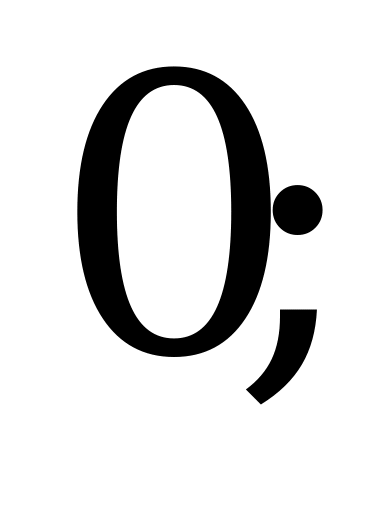
 ,
, 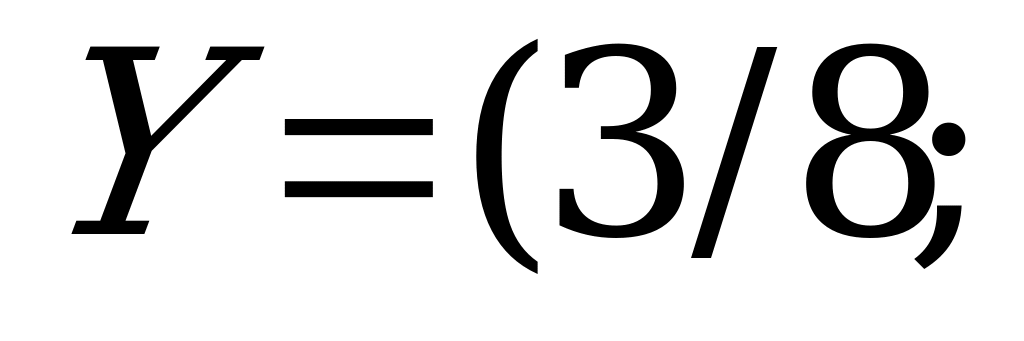
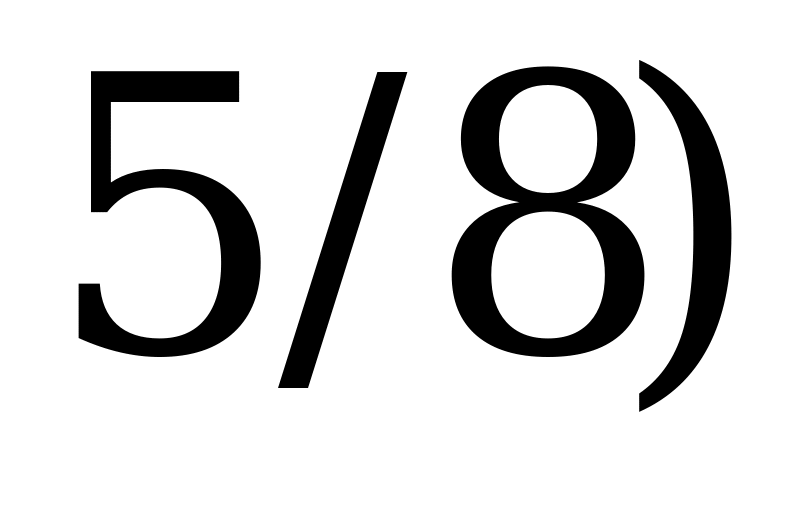 ,
, 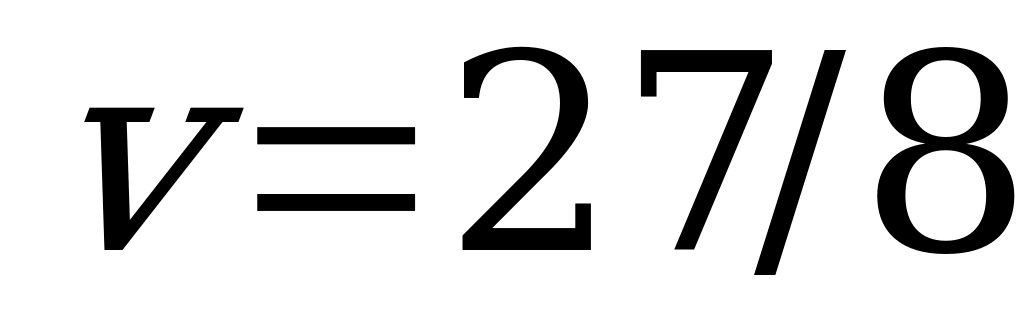 .
.
Е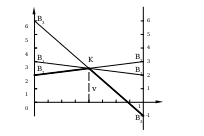 сли в точке
сли в точке 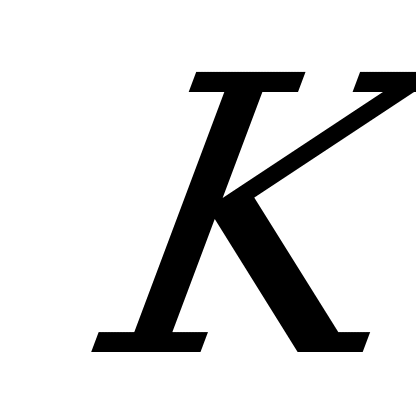 пересекается более двух прямых, то для другого игрока возможны несколько оптимальных смешанных стратегий.
пересекается более двух прямых, то для другого игрока возможны несколько оптимальных смешанных стратегий. 


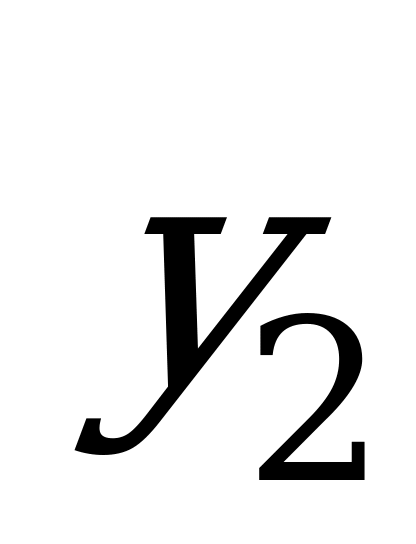


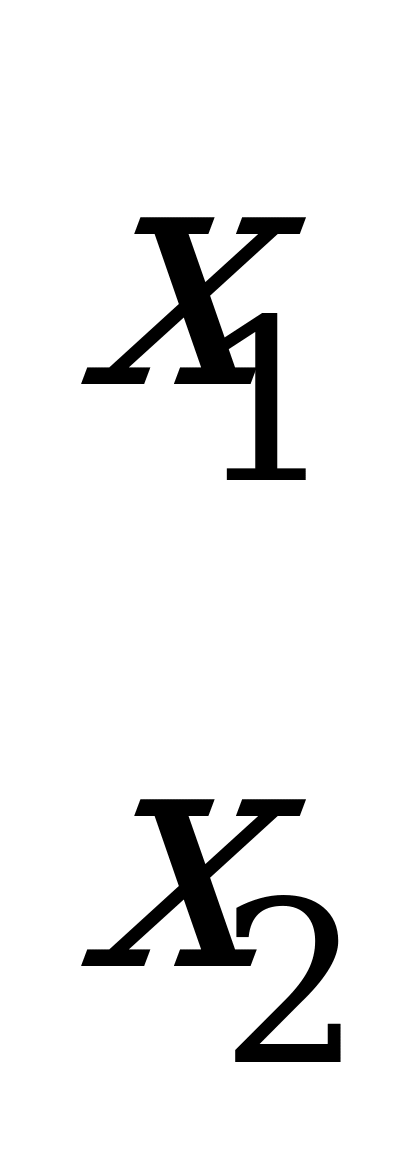



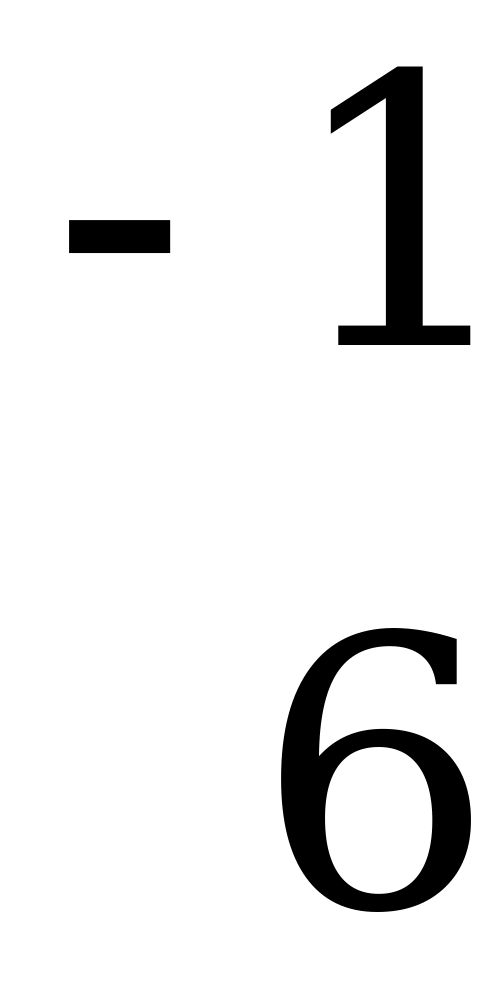

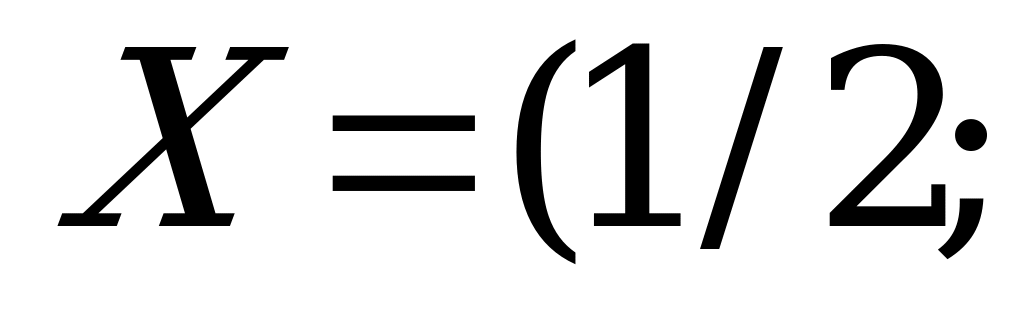
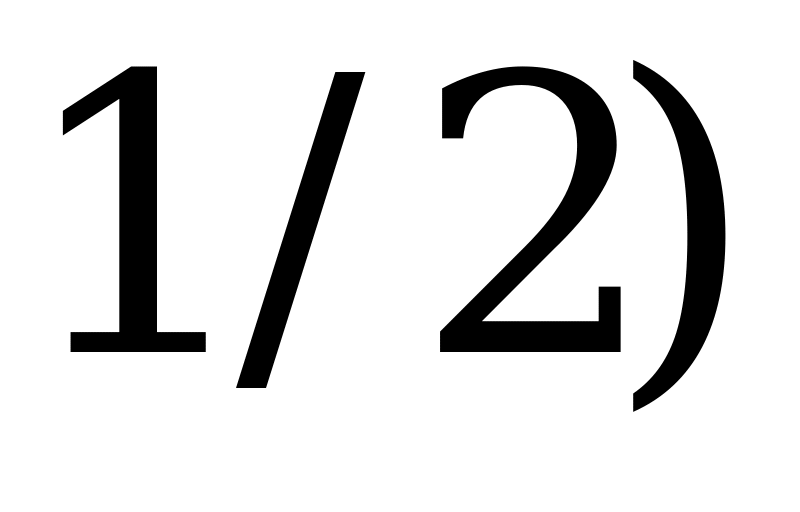

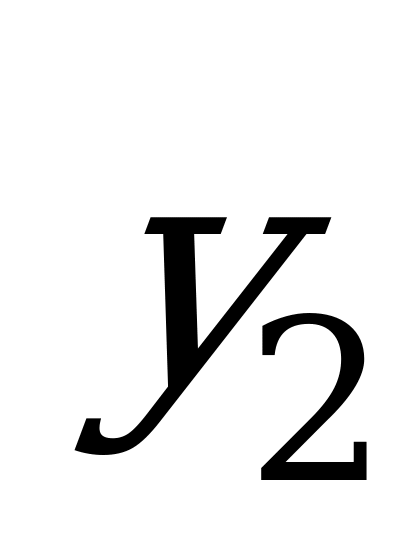


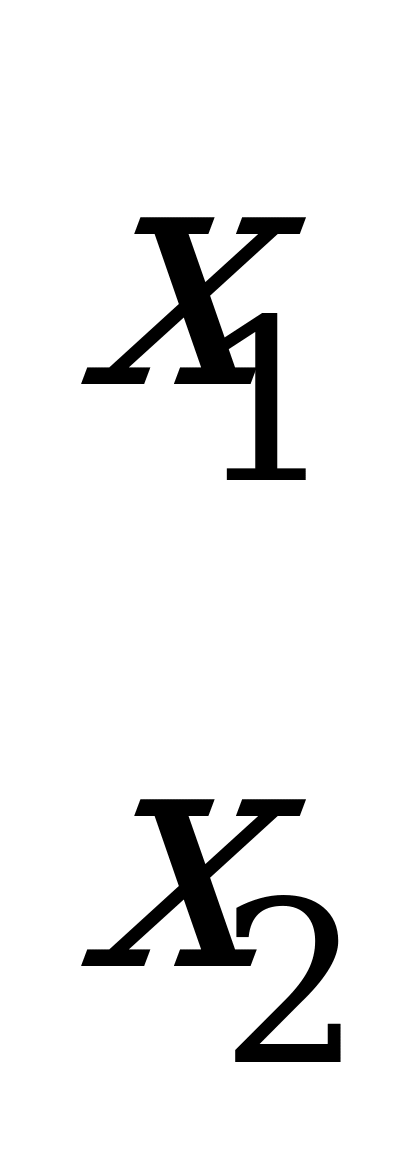


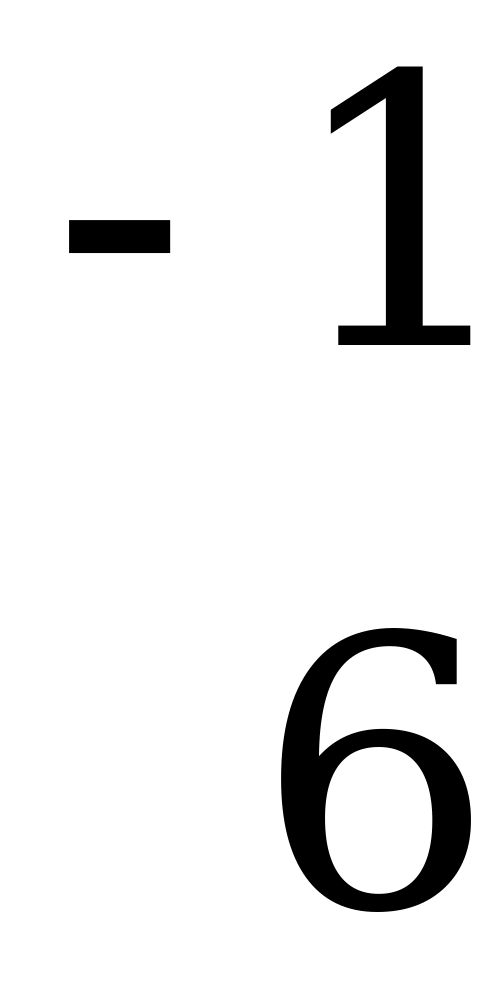
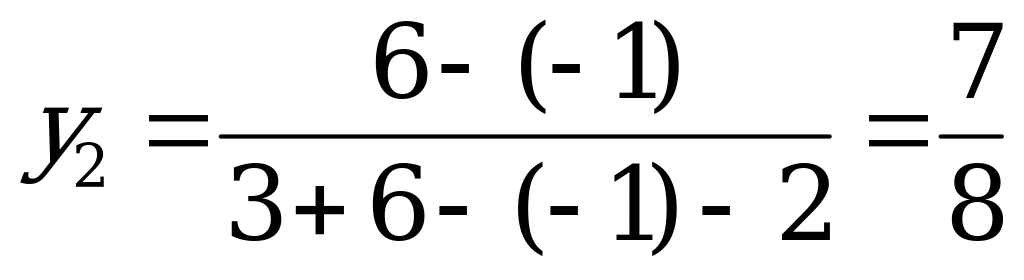 ,
, 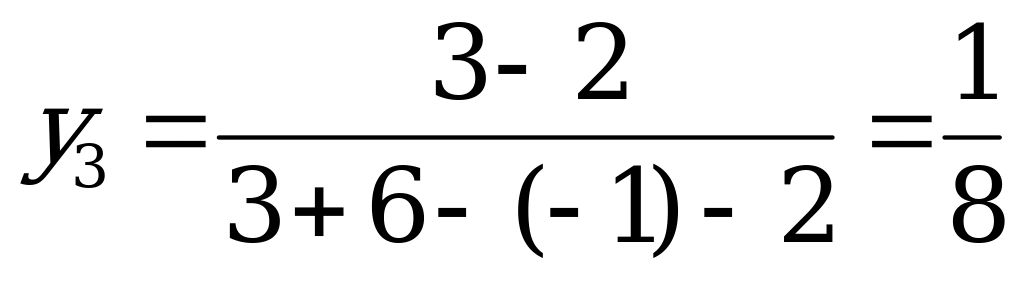 ,
, 
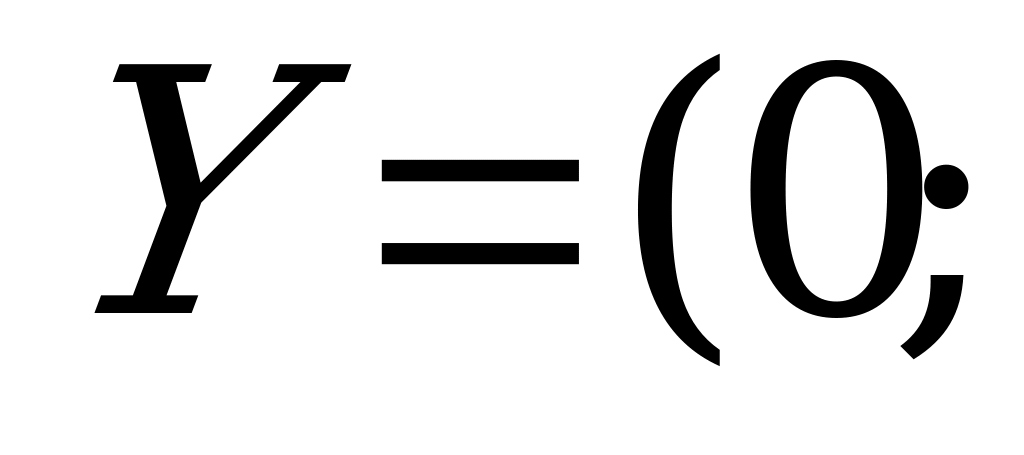
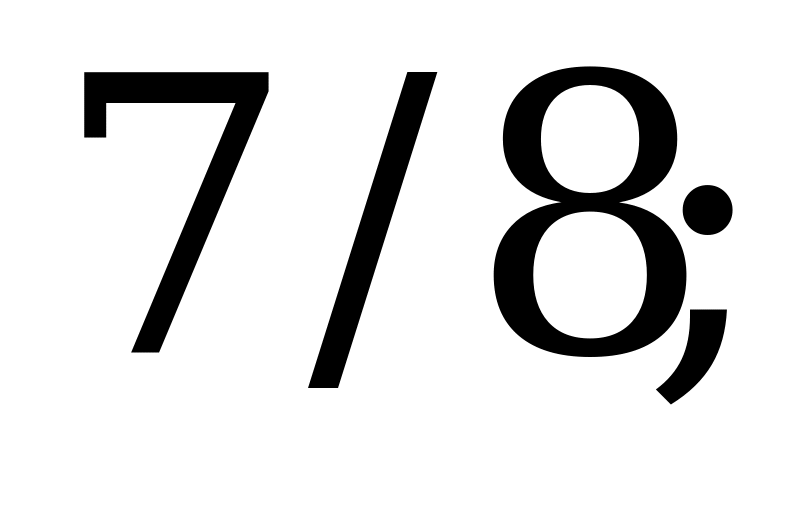
 ,
, 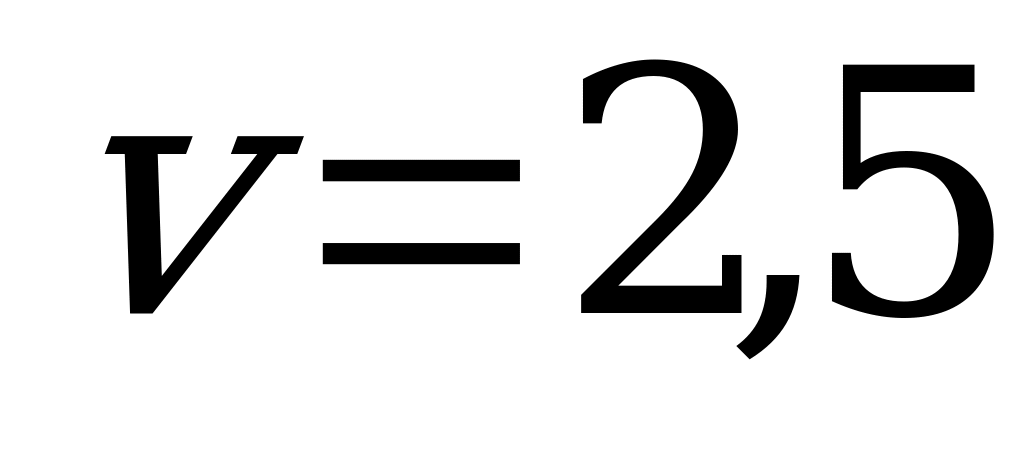 .
.


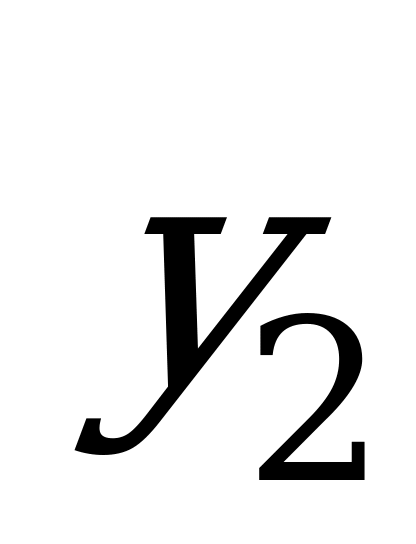


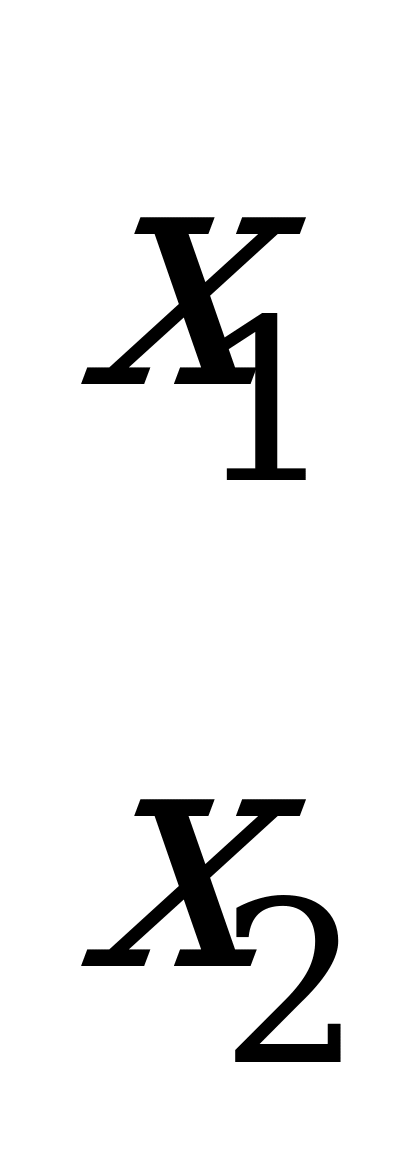

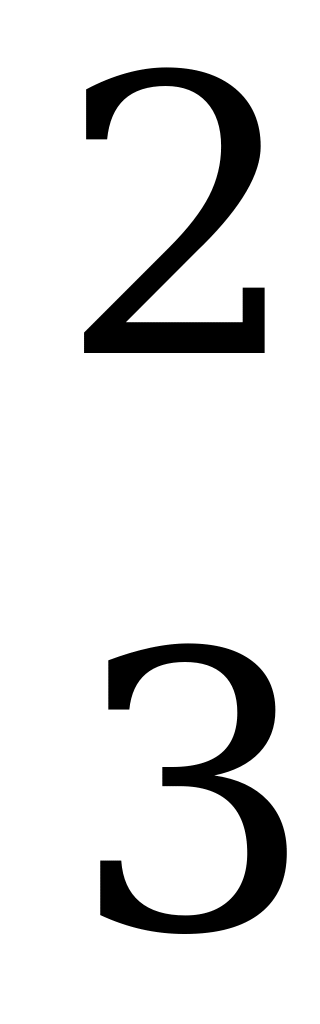

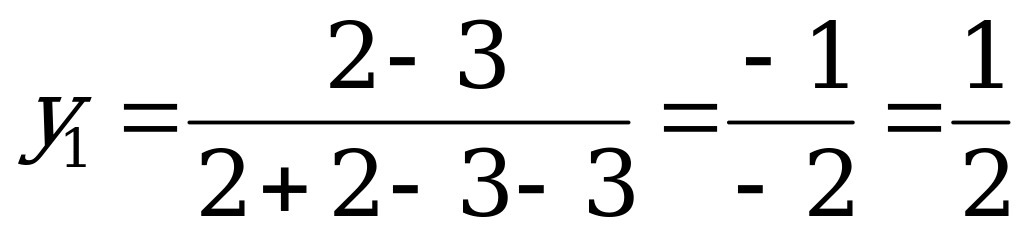 ,
, 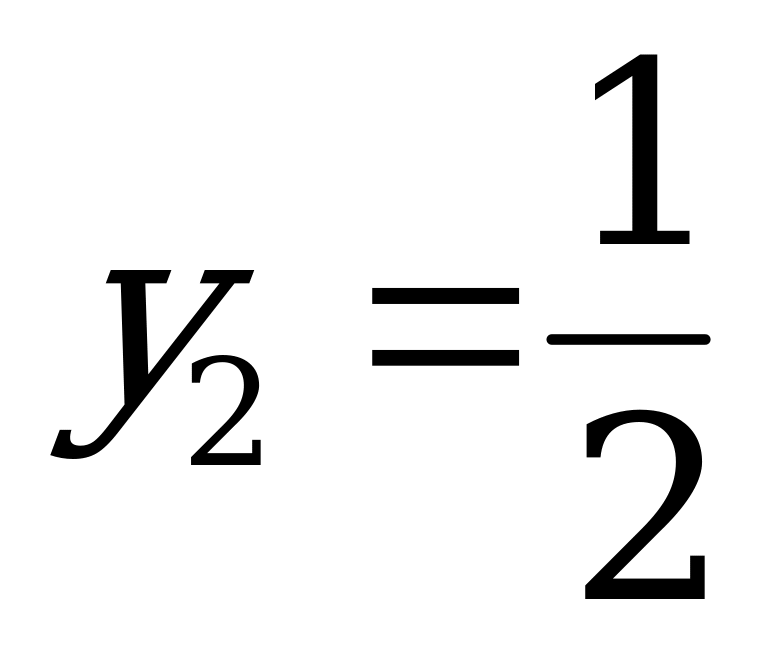 ,
, 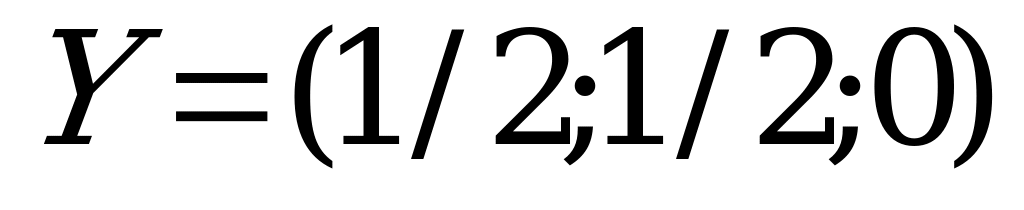 ,
, 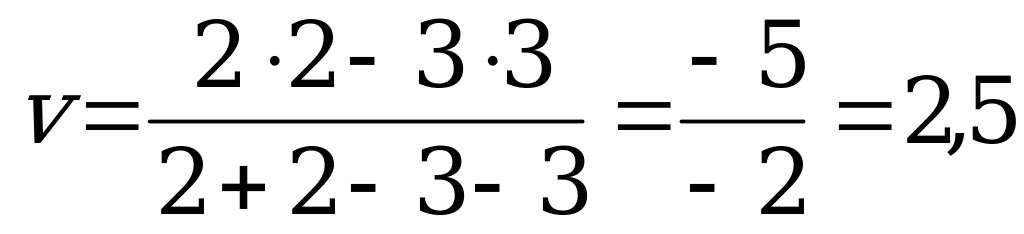 .
.





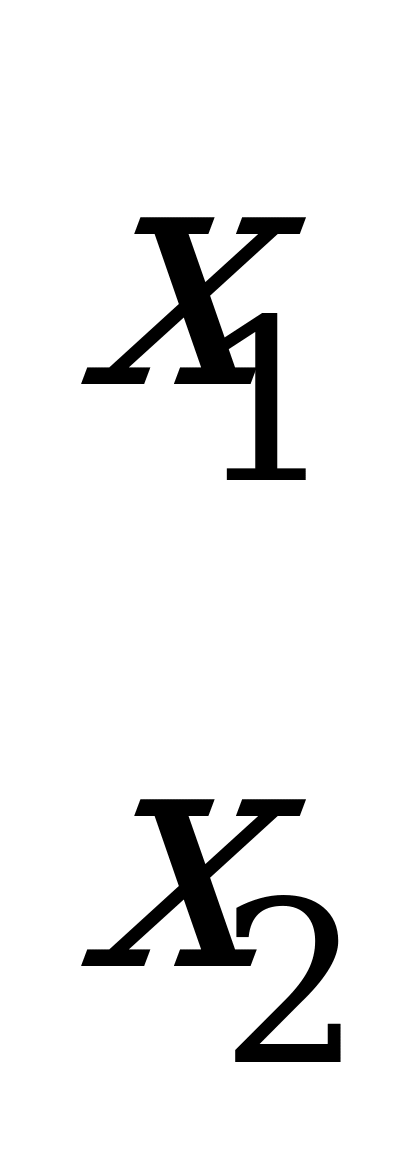

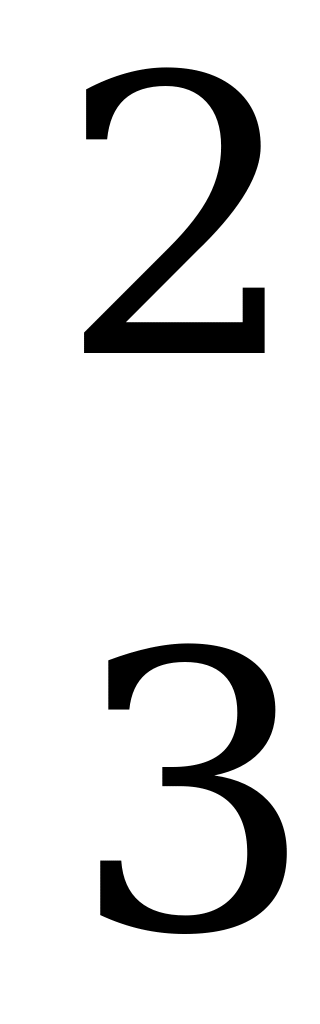
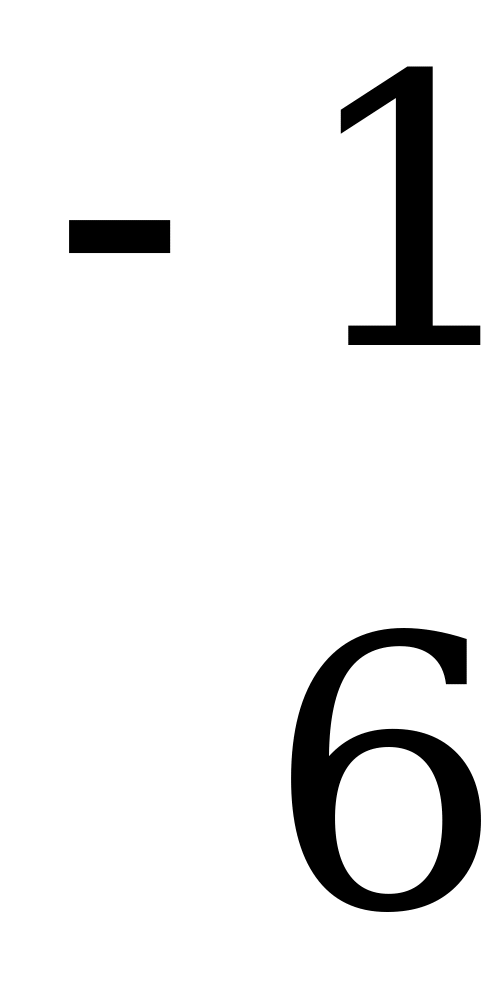
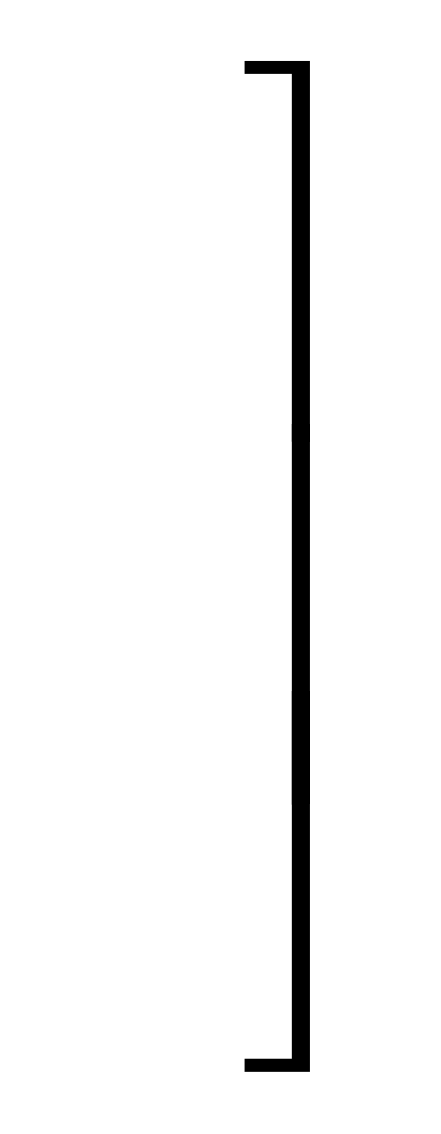
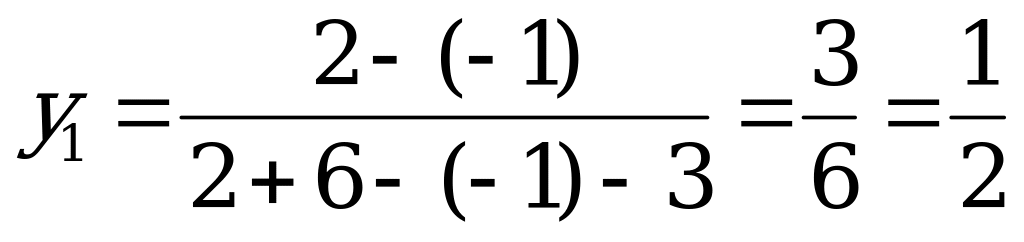 ,
, 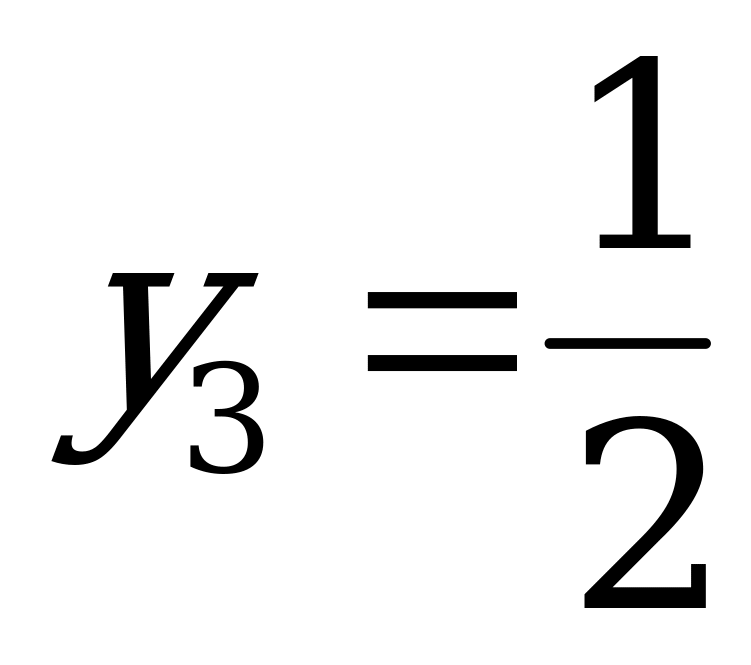 ,
, 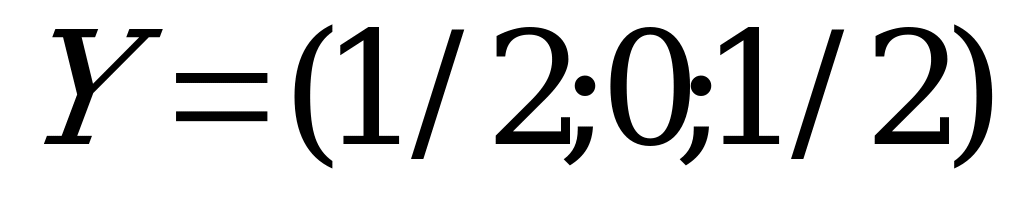 ,
, 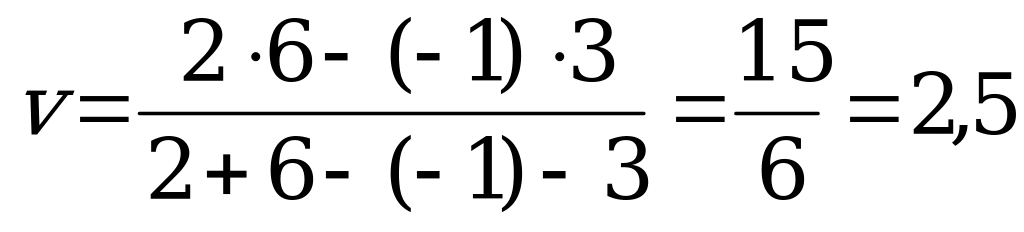 .
.
Сведение матричной игры к задаче линейного программирования
Рассмотрим игру, матрица которой имеет размерность 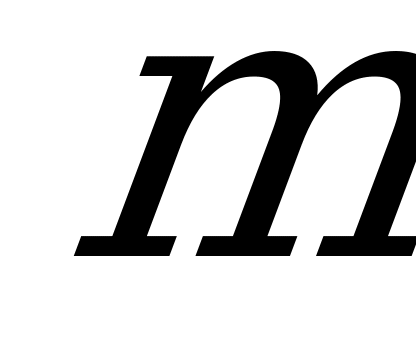 ×
×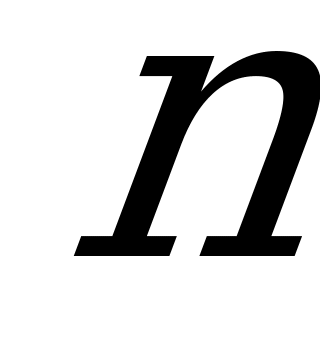 :
:



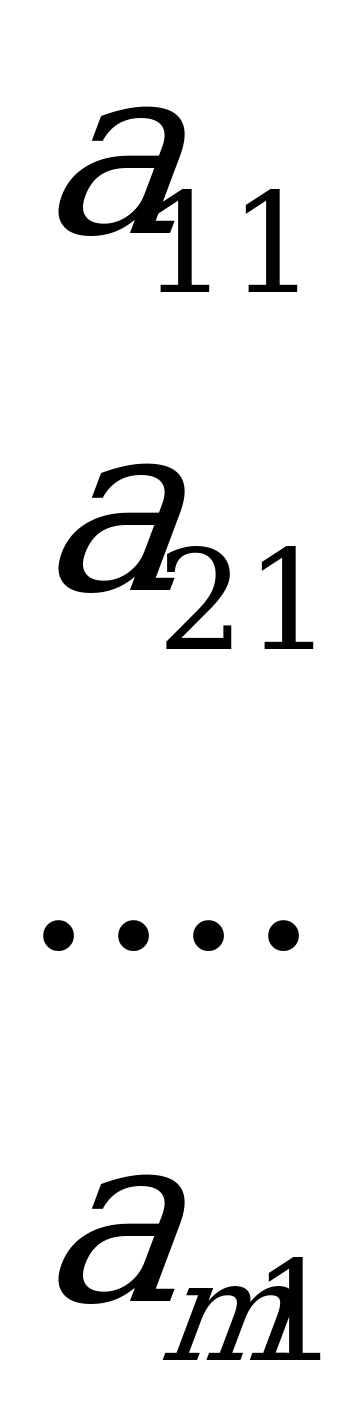


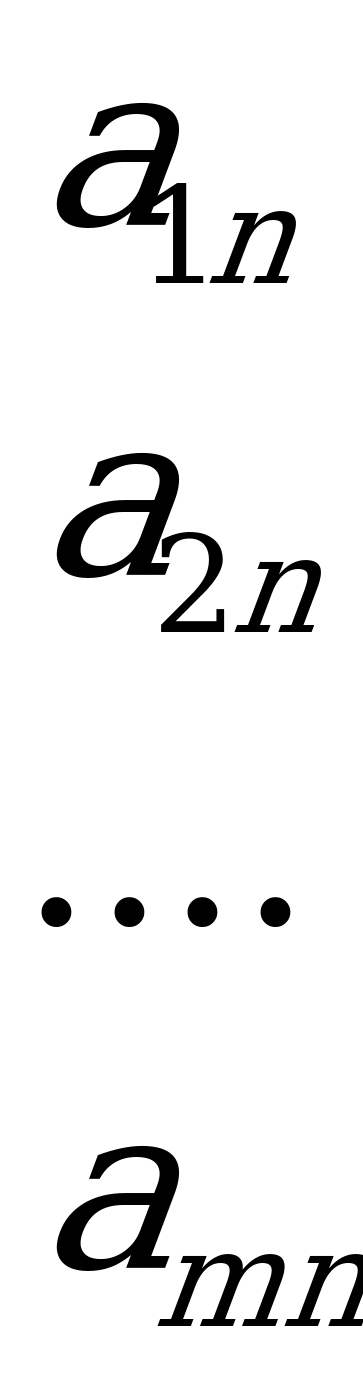
 .
.
Обозначим через 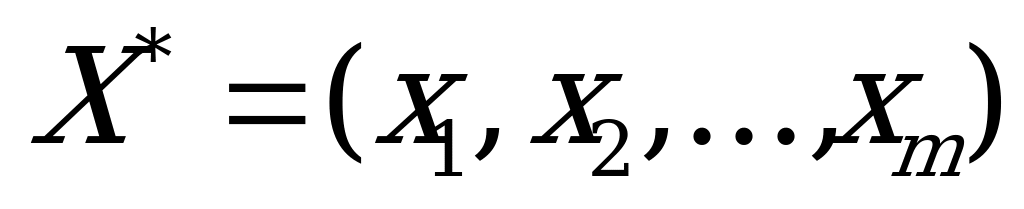 ,
, 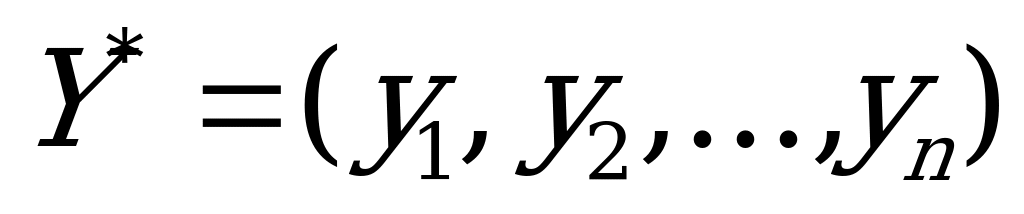 оптимальные смешанные стратегии игроков
оптимальные смешанные стратегии игроков  и
и  . Стратегия
. Стратегия 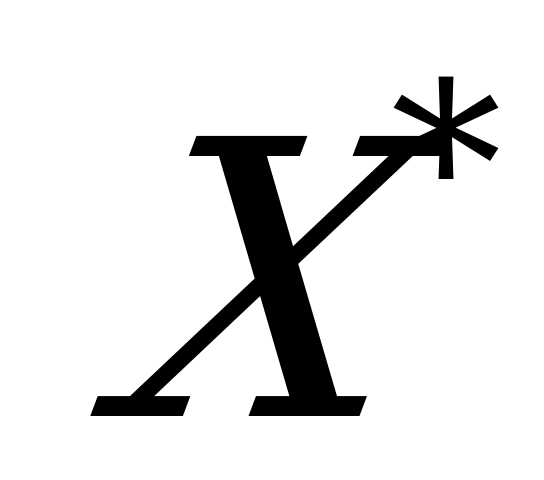 игрока
игрока  гарантирует ему выигрыш не меньше
гарантирует ему выигрыш не меньше  , независимо от выбора стратегии
, независимо от выбора стратегии  игроком
игроком  . Это можно записать так:
. Это можно записать так:
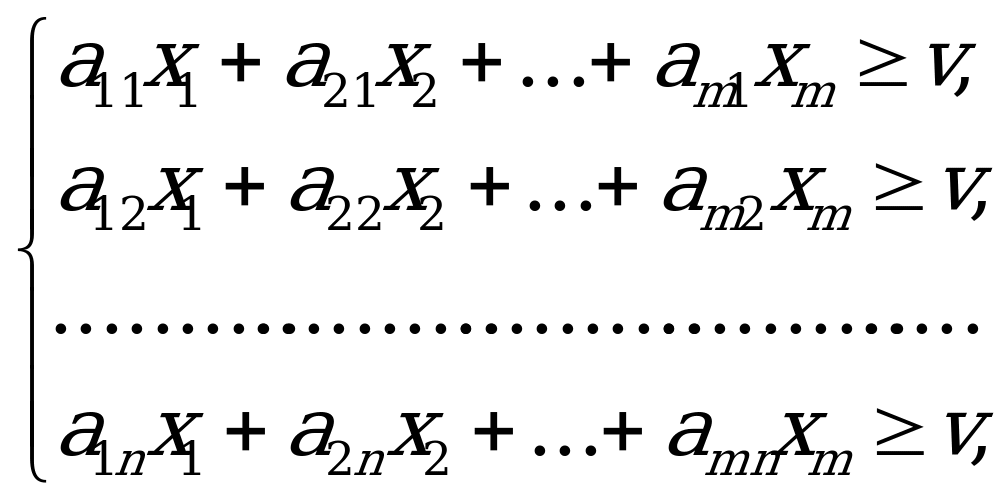 (5.1)
(5.1)
где 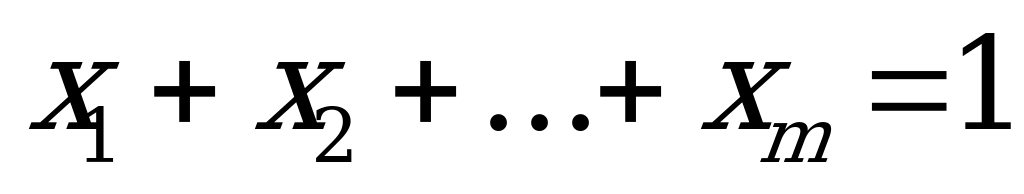 ;
;
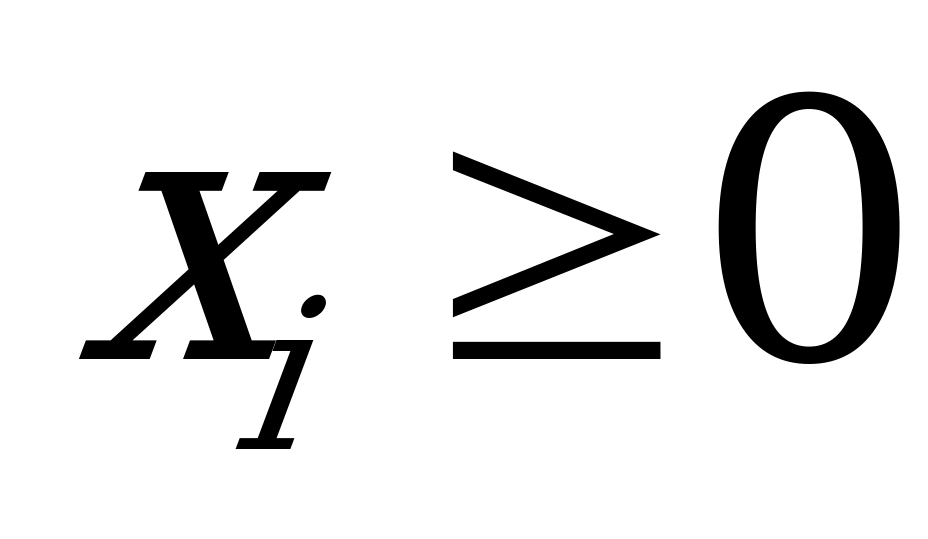
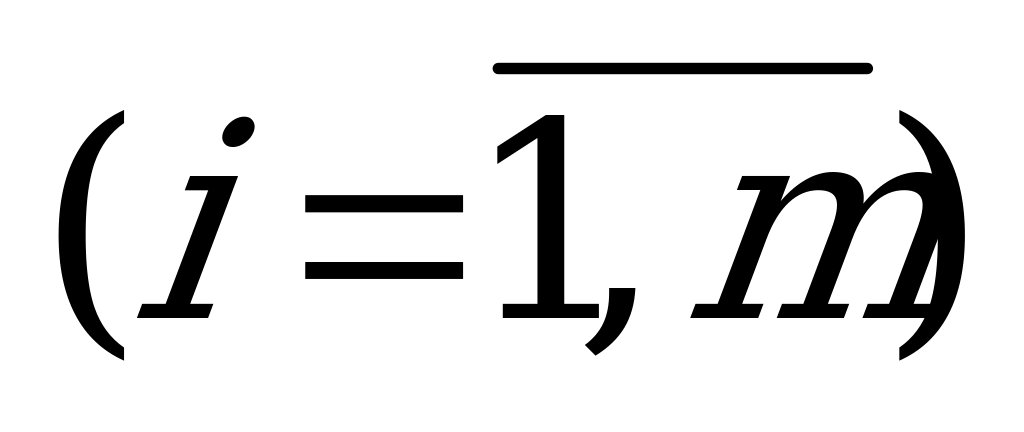 .
.
Аналогично стратегия  игрока
игрока  гарантирует ему проигрыш не больше
гарантирует ему проигрыш не больше  , независимо от выбора стратегии
, независимо от выбора стратегии  игроком
игроком  , т.е.
, т.е.
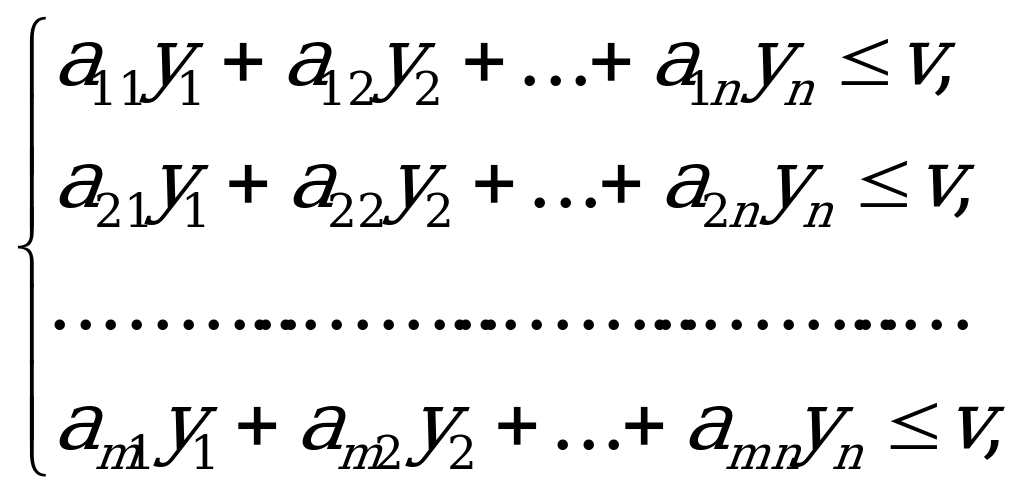 (5.2)
(5.2)
где 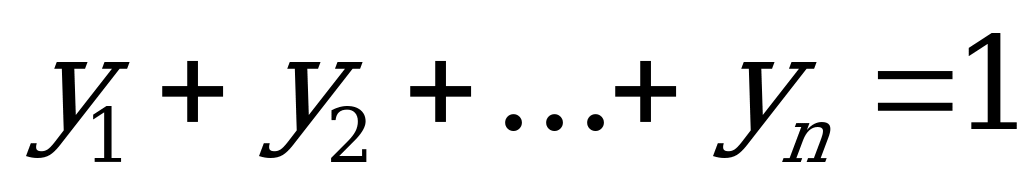 ;
;
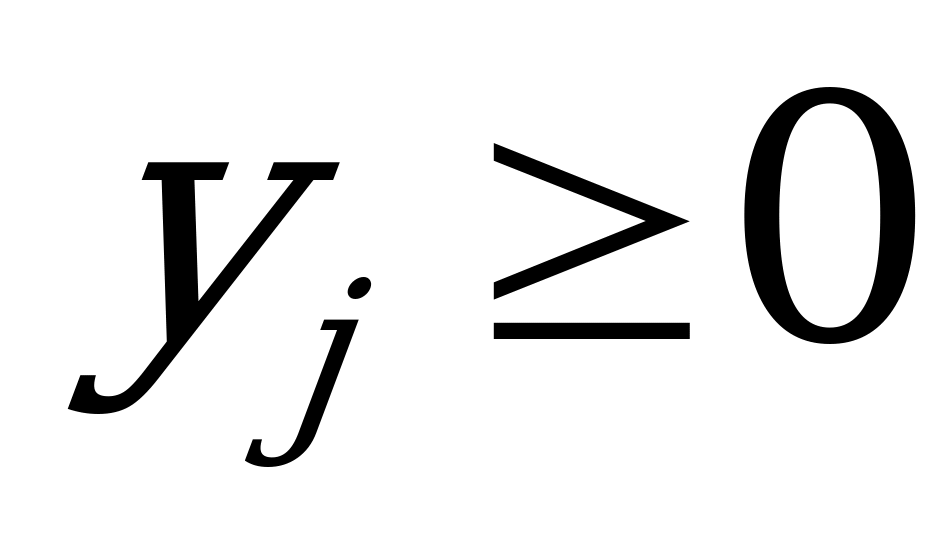
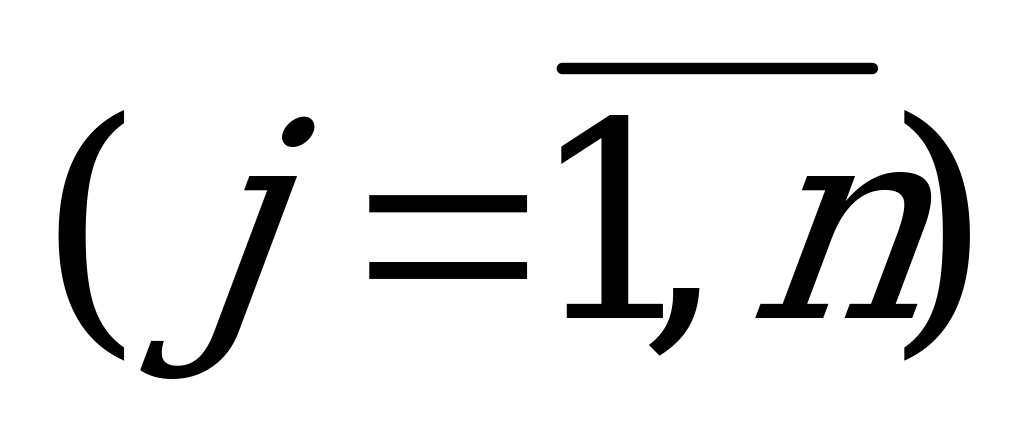 .
.
Величина  (цена игры) не известна, однако можно считать, что
(цена игры) не известна, однако можно считать, что 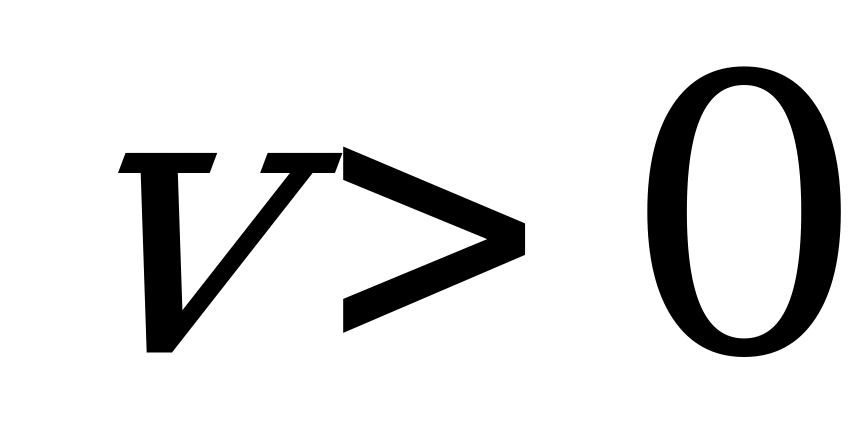 . Последнее условие выполняется всегда, если элементы матрицы неотрицательны, а этого можно достигнуть, прибавляя ко всем элементам матрицы некоторое положительное число. Преобразуем системы (5.1) и (5.2), разделив обе части каждого неравенства на положительное число
. Последнее условие выполняется всегда, если элементы матрицы неотрицательны, а этого можно достигнуть, прибавляя ко всем элементам матрицы некоторое положительное число. Преобразуем системы (5.1) и (5.2), разделив обе части каждого неравенства на положительное число  , и введём новые обозначения
, и введём новые обозначения 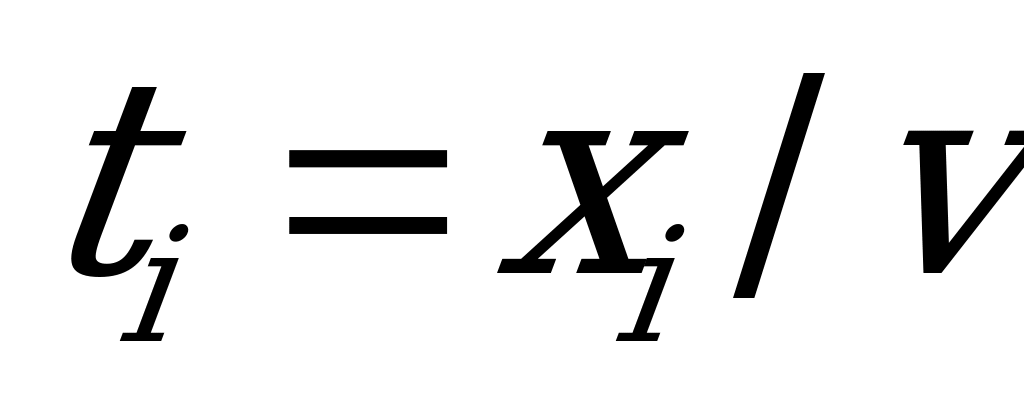 ,
, 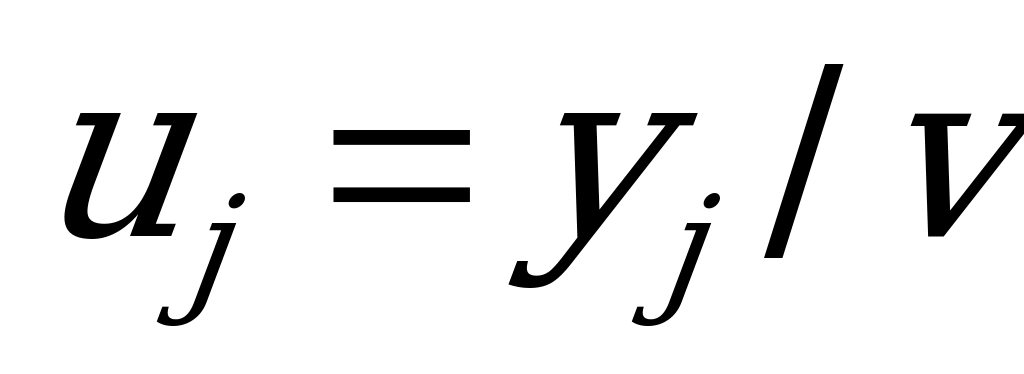
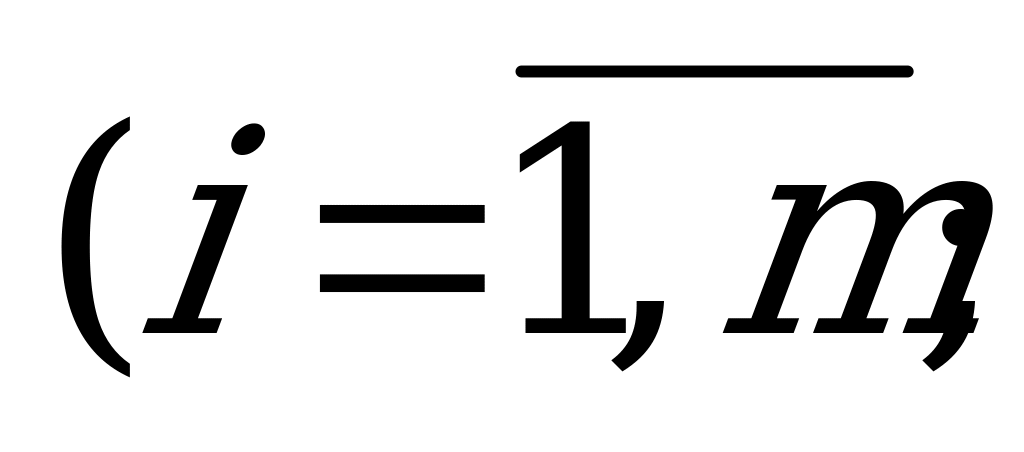
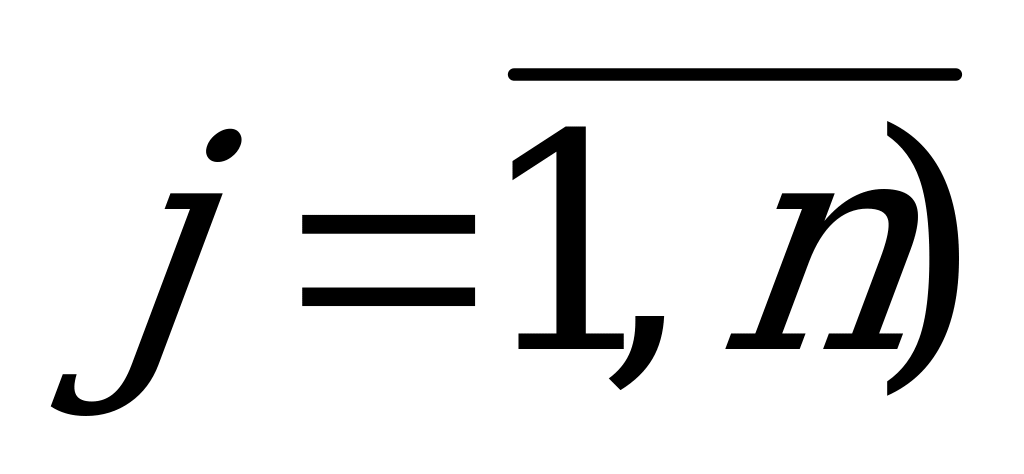 .
.
Получим: 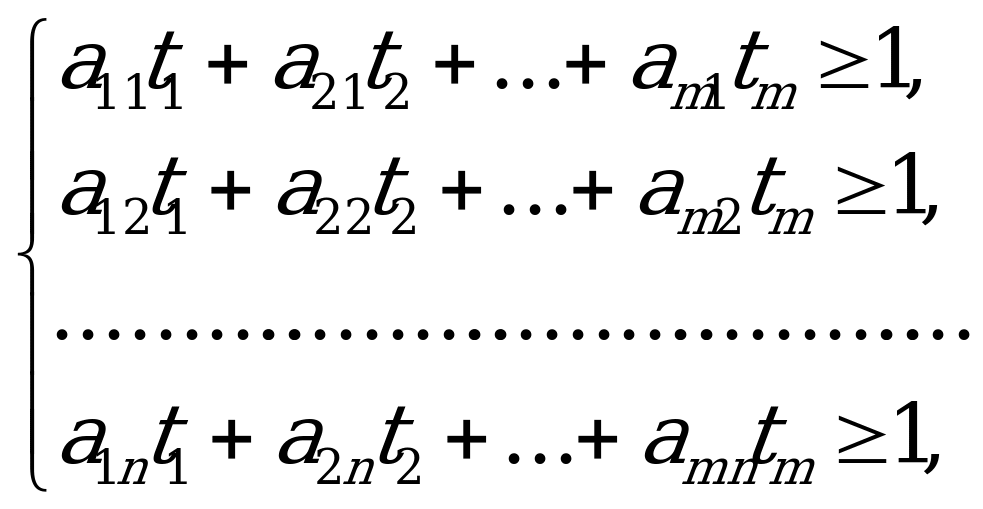 (6.1)
(6.1)
где 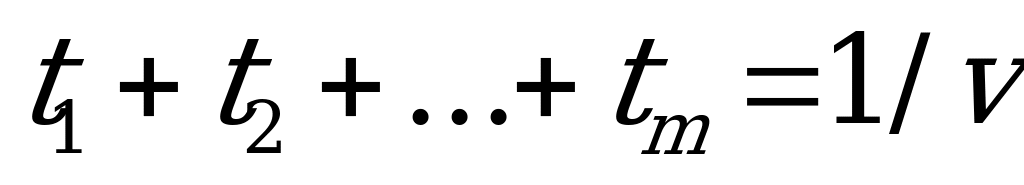 ; (6.2)
; (6.2)
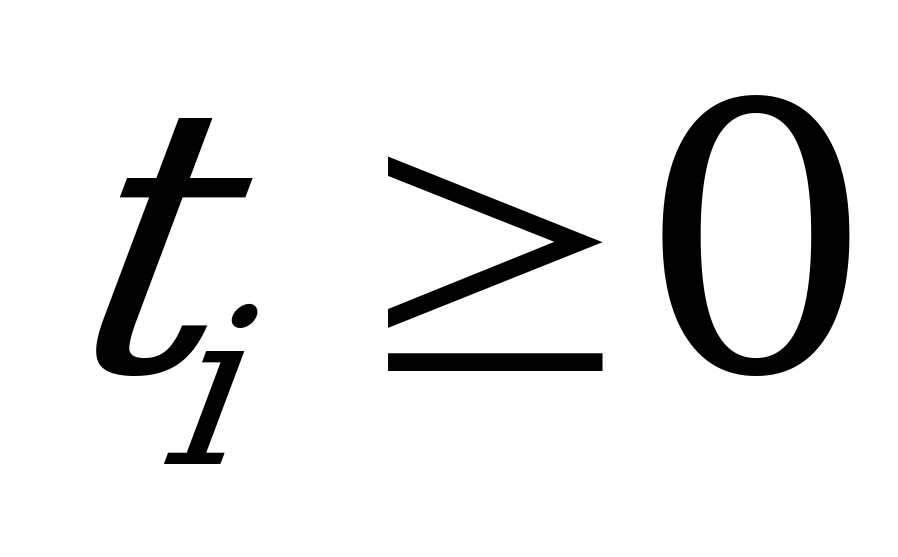
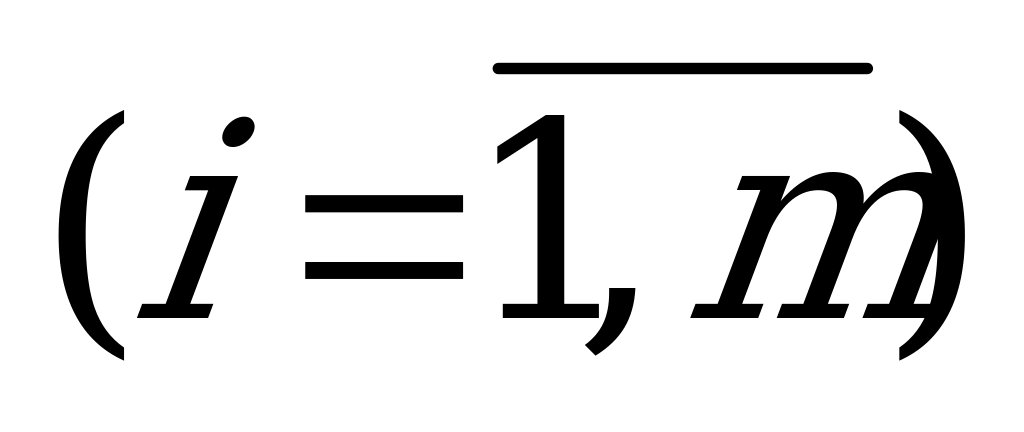 ,
,
и 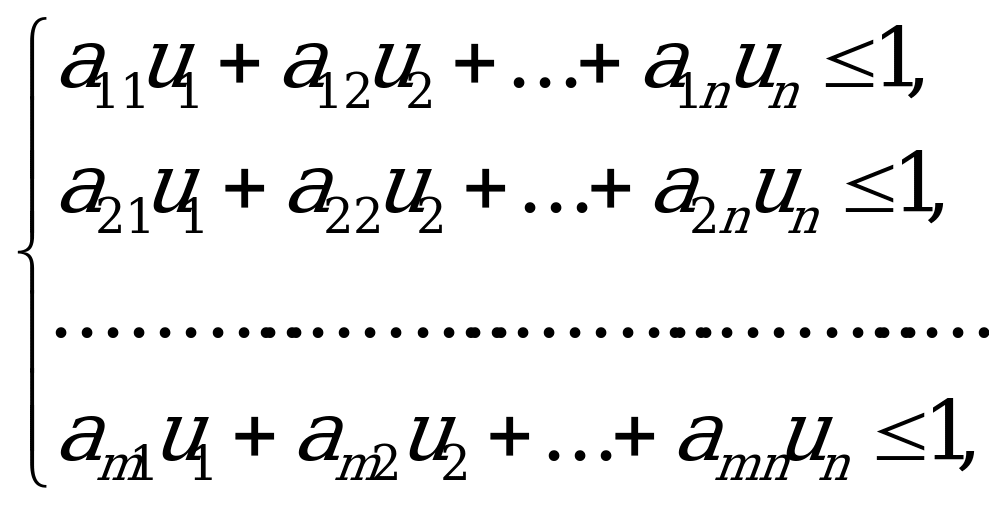 (6.3)
(6.3)
где 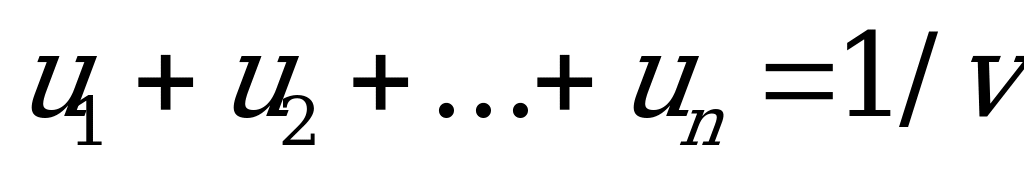 ; (6.4)
; (6.4)
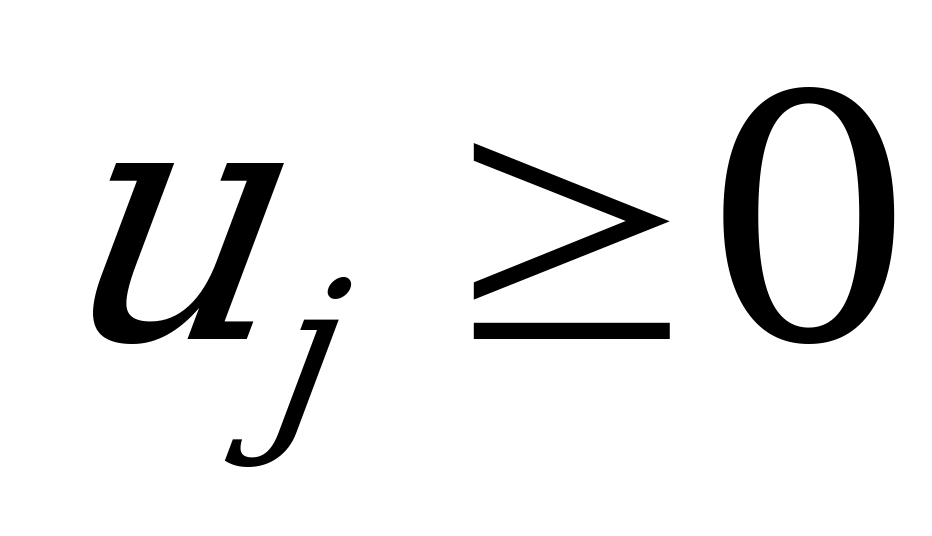
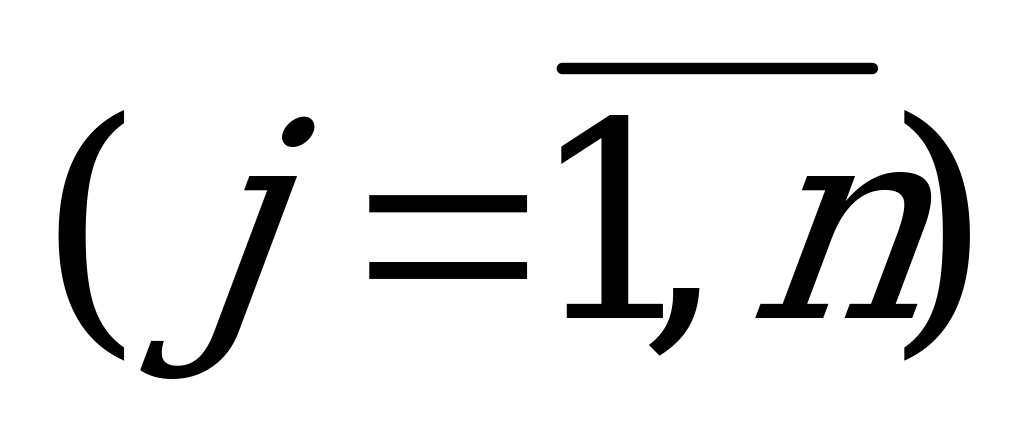 .
.
Так как игрок  стремится максимизировать цену игры
стремится максимизировать цену игры  , то обратная величина
, то обратная величина  будет минимизироваться, поэтому оптимальная стратегия игрока A определится из задачи линейного программирования следующего вида:
будет минимизироваться, поэтому оптимальная стратегия игрока A определится из задачи линейного программирования следующего вида:
найти минимальное значение функции 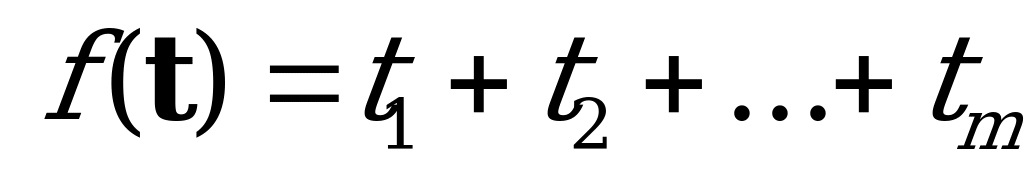 при ограничениях (6.1), (6.2).
при ограничениях (6.1), (6.2).
Оптимальная смешанная стратегия игрока B определится решением задачи следующего вида:
найти максимальное значение функции 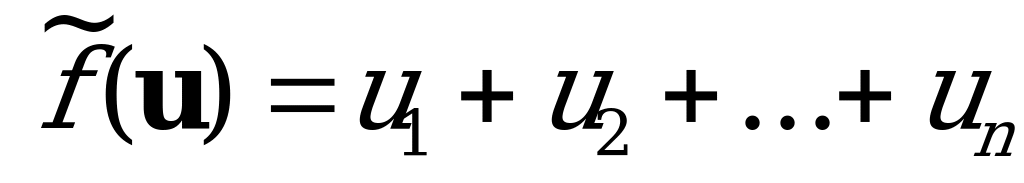 при ограничениях (6.3), (6.4).
при ограничениях (6.3), (6.4).
Таким образом, для решения игры имеем пару двойственных симметричных задач линейного программирования. Используя свойство симметричности, можно решить одну из них, требующую меньших вычислений, а решение второй задачи найти на основании оптимального плана двойственной.
Далее определим: 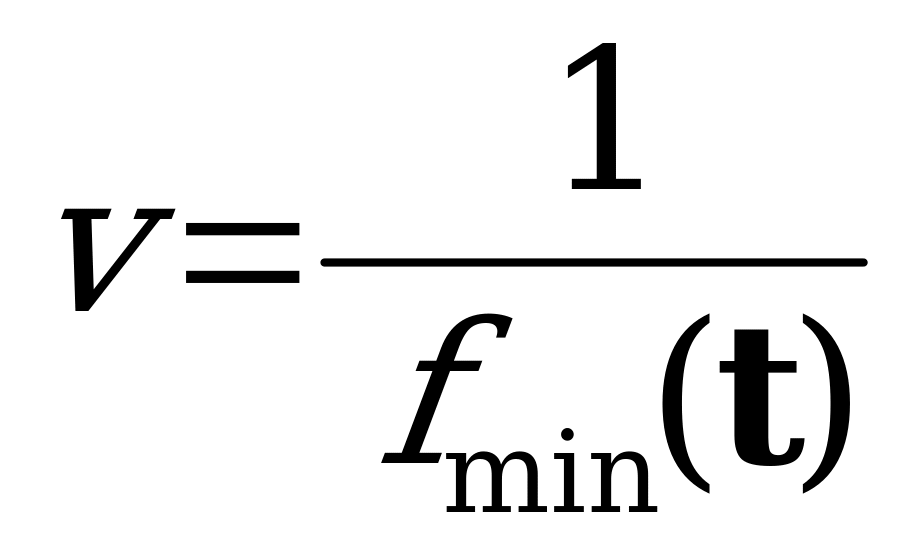
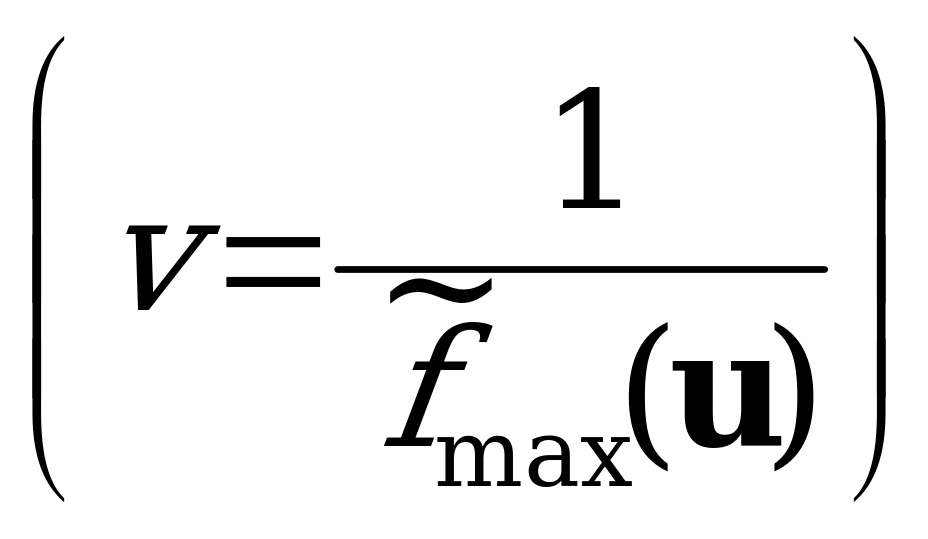 ,
, 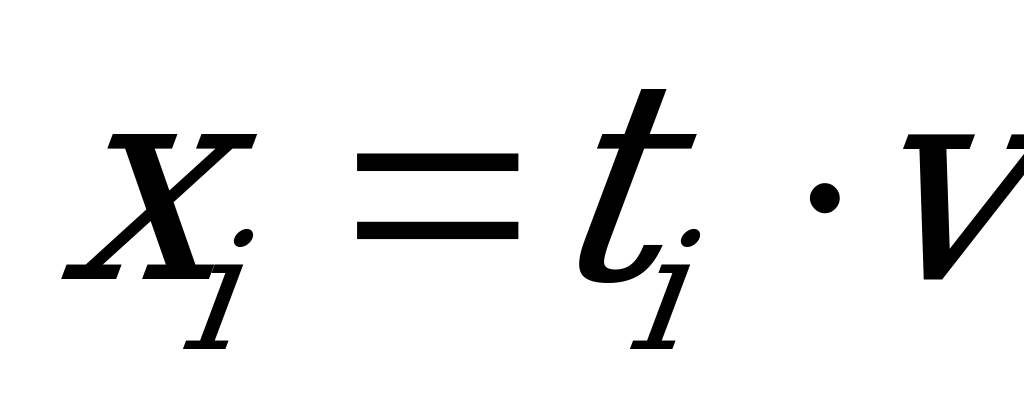 ,
, 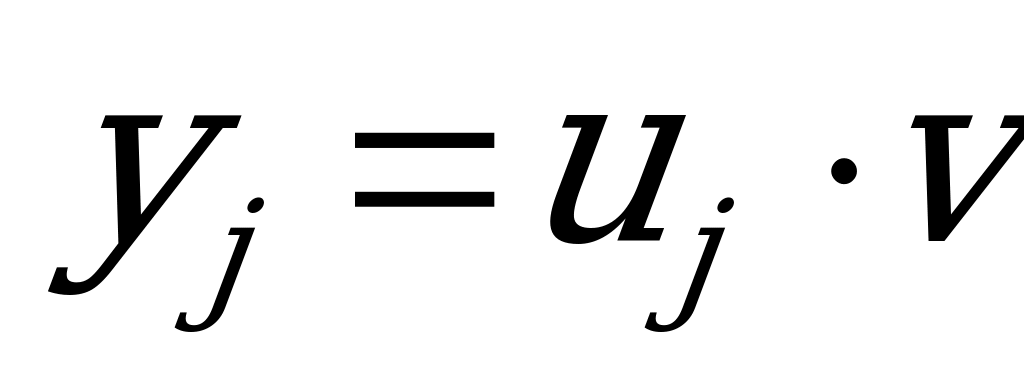
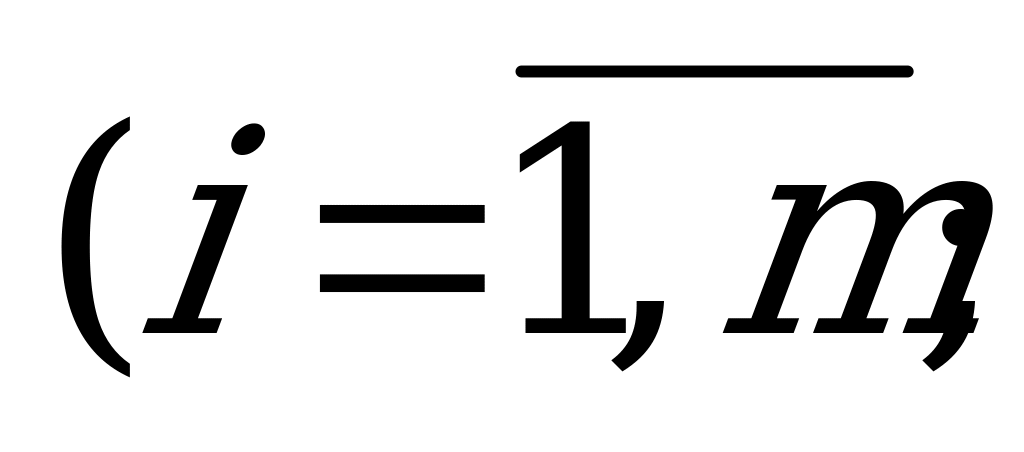
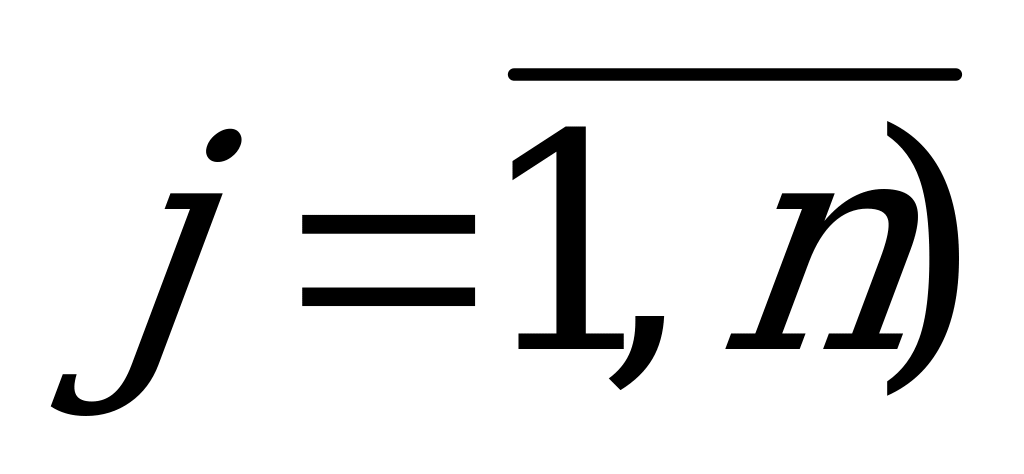 .
.
Пример 9-а. 
Найти решение игры, заданной матрицей: 




 .
.
Решение. Проверим игру на наличие седловой точки:
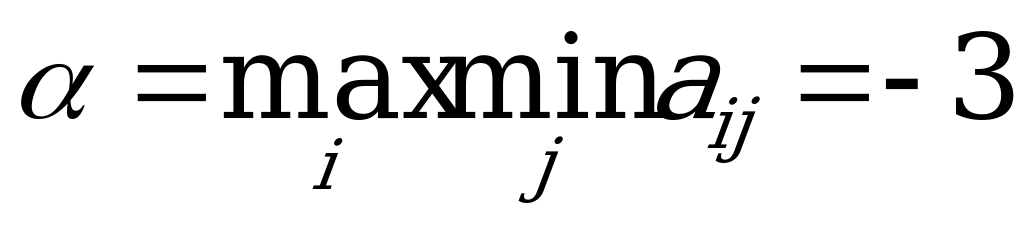 ,
, 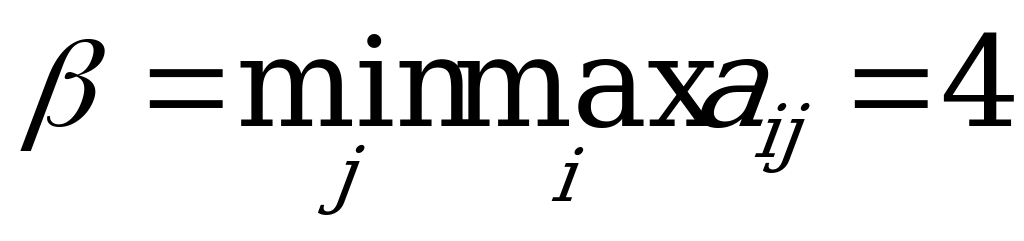 ,
, 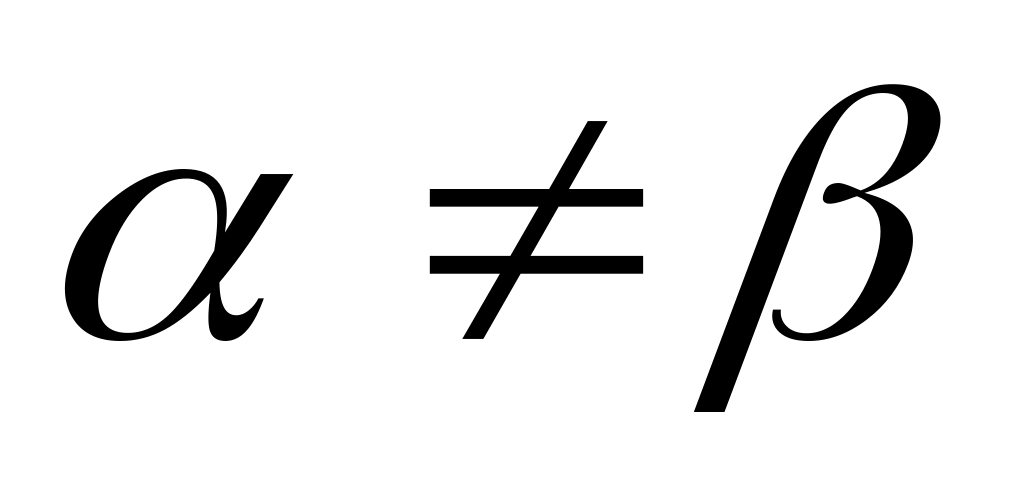 ,
,
поэтому решение игры определяем в смешанных стратегиях. Цена игры  заключена между нижней
заключена между нижней  и верхней
и верхней 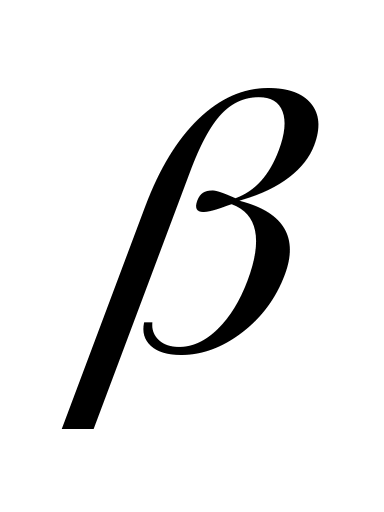 ценами, т.е.
ценами, т.е. 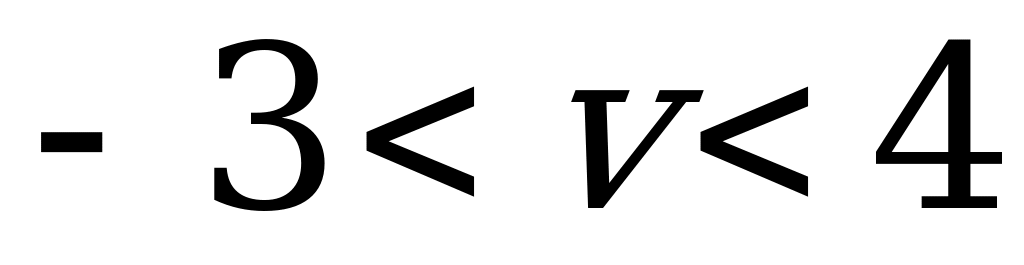 .
.
Составим ЗЛП для каждого игрока.
Чтобы избавиться от отрицательных чисел в матрице игры, прибавим к элементам матрицы число 5; при этом цена игры увеличится на 5, а решение 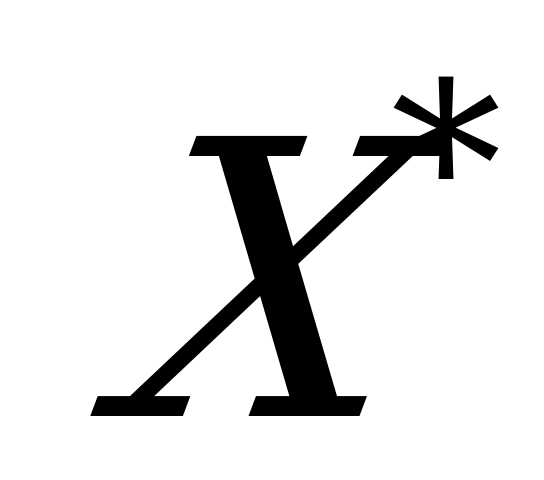 ,
, 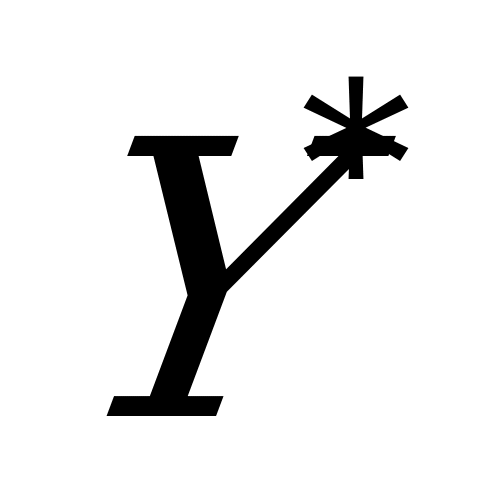 не изменится:
не изменится:



 .
.
Для игрока  : найти минимальное значение функции
: найти минимальное значение функции
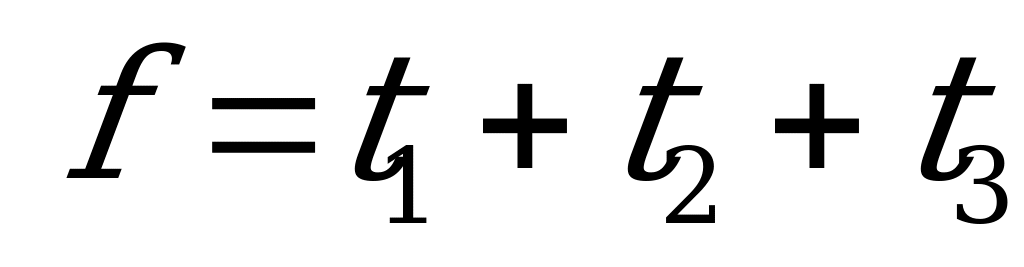
при ограничениях 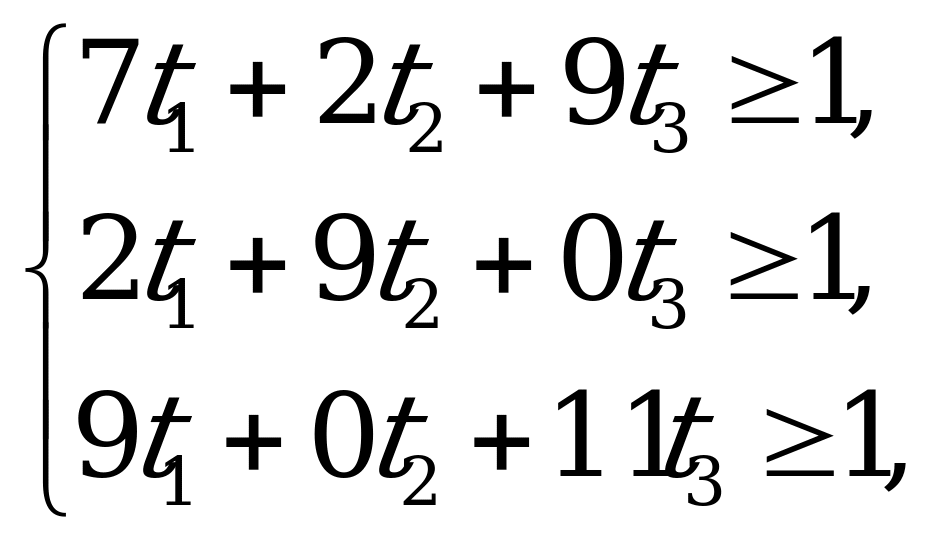
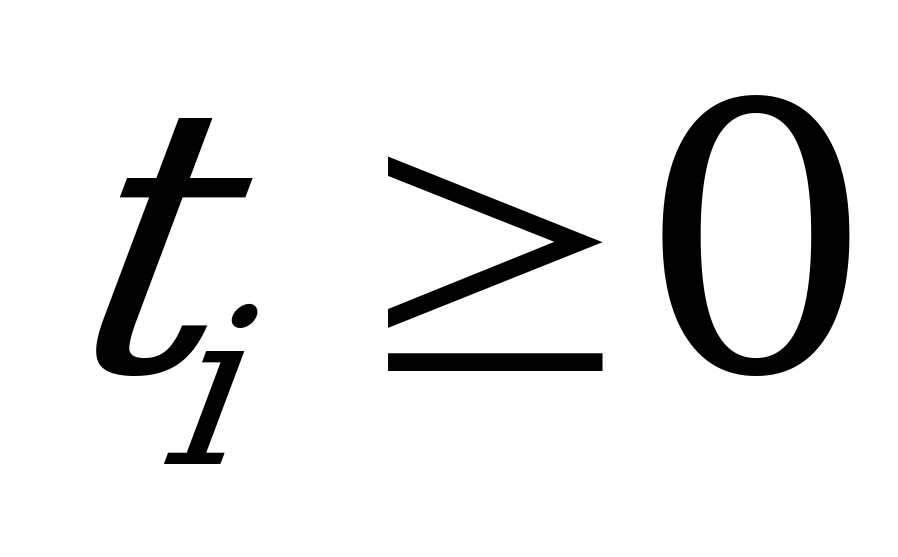
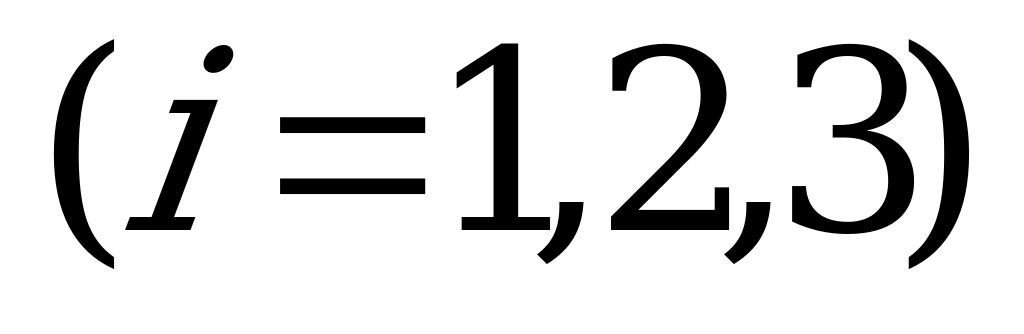 .
.
Для игрока  : найти максимальное значение функции
: найти максимальное значение функции 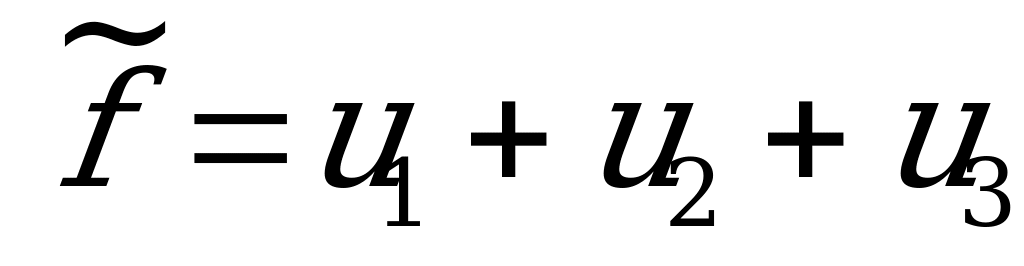
при ограничениях 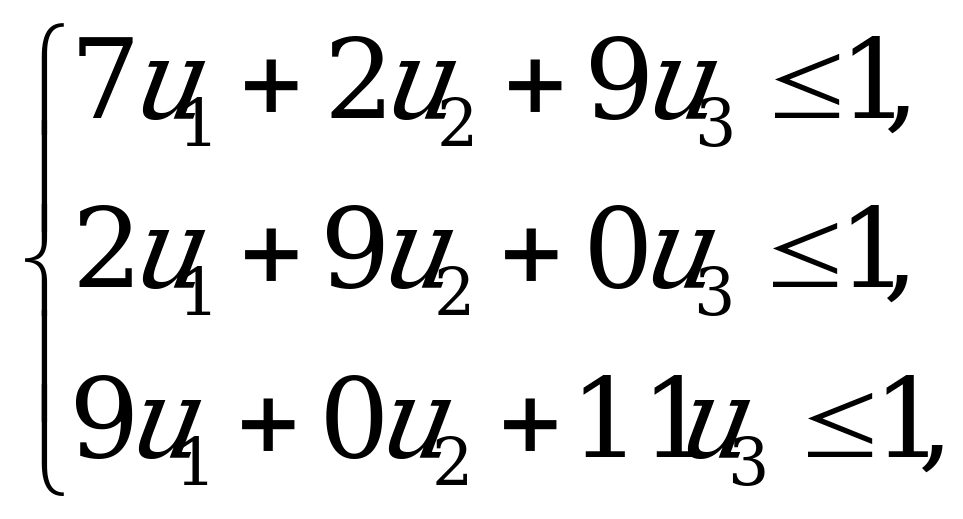
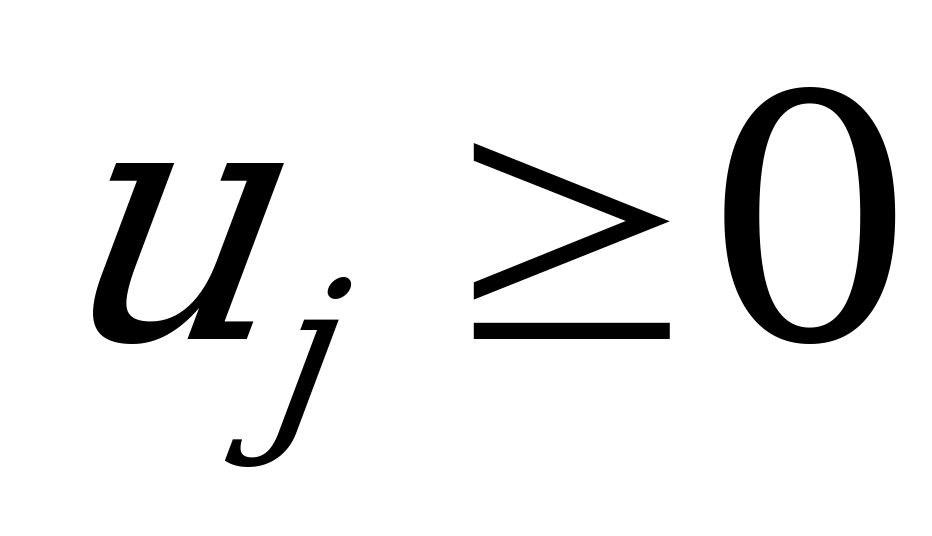
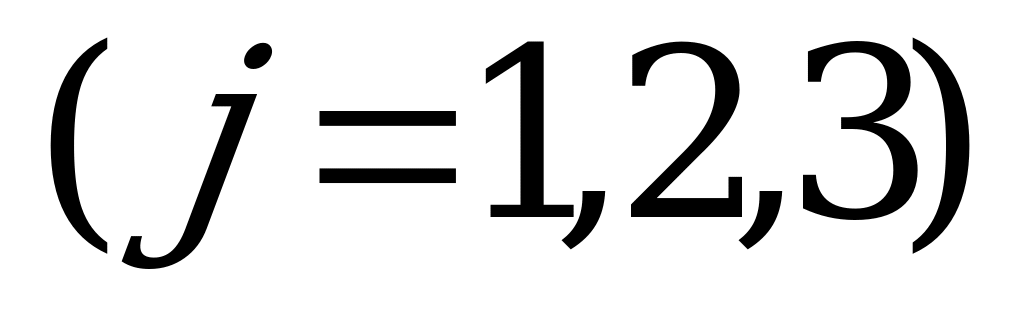 .
.
Вводя дополнительные переменные 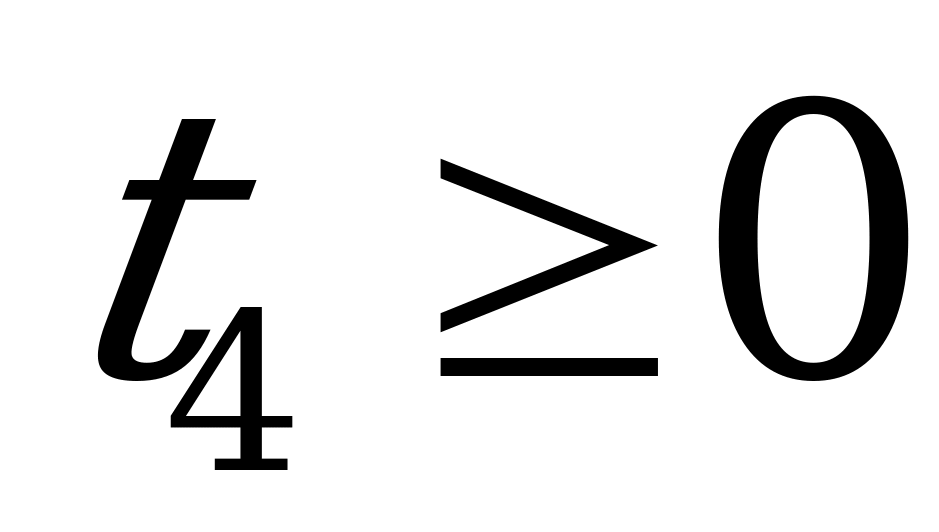 ,
, 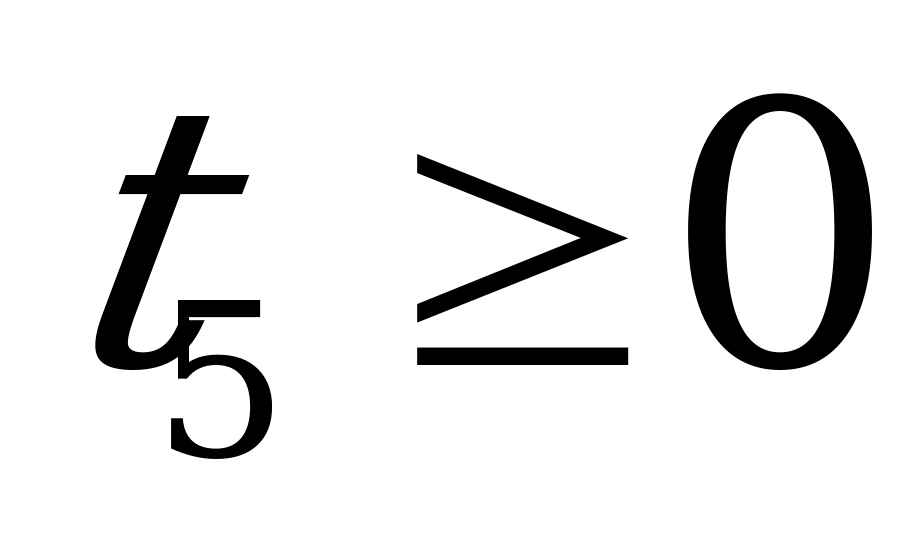 ,
, 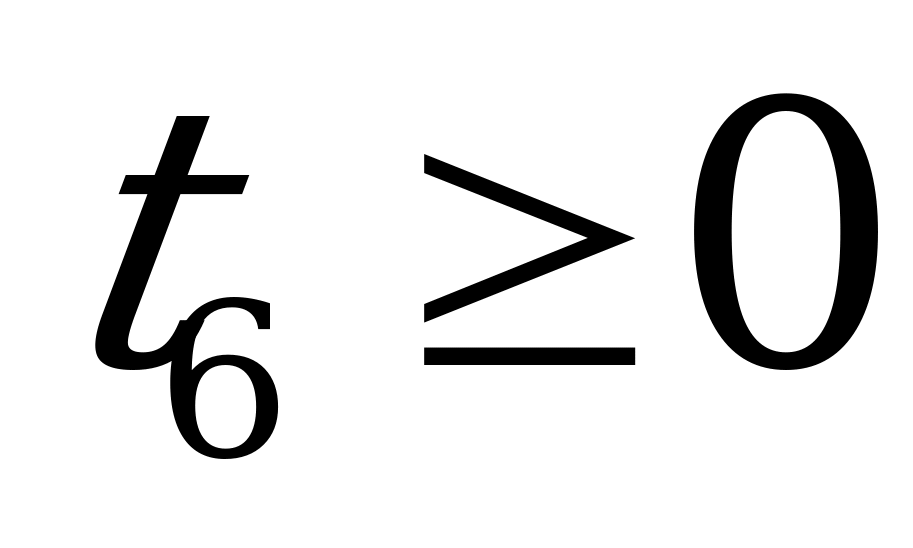 (для
(для  -задачи) и
-задачи) и 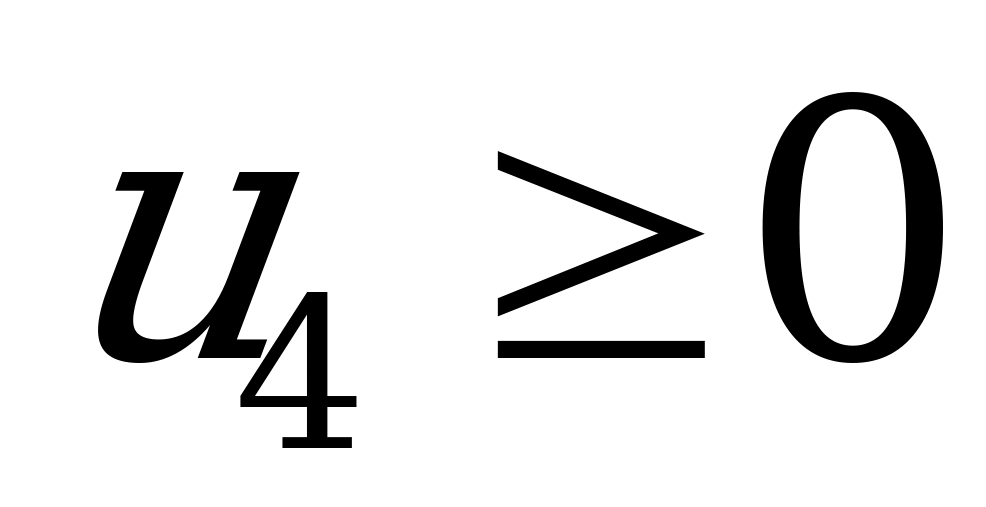 ,
, 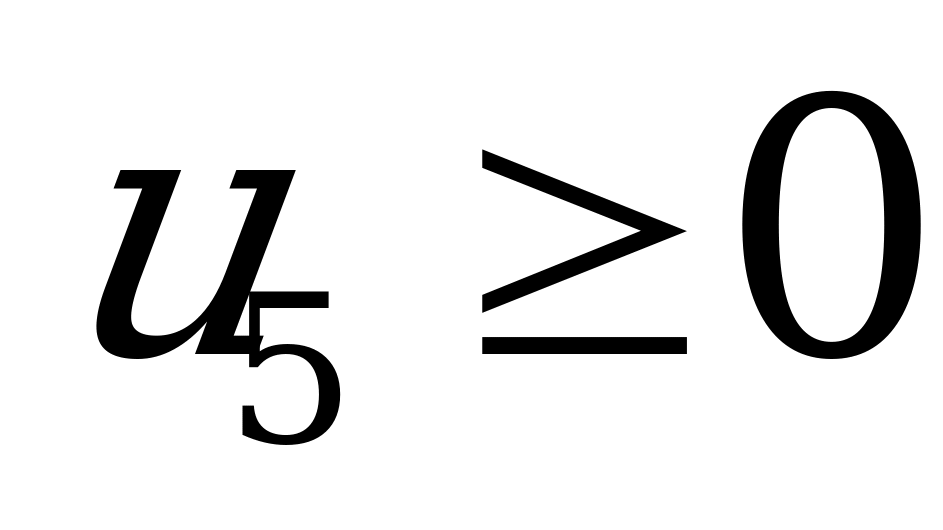 ,
, 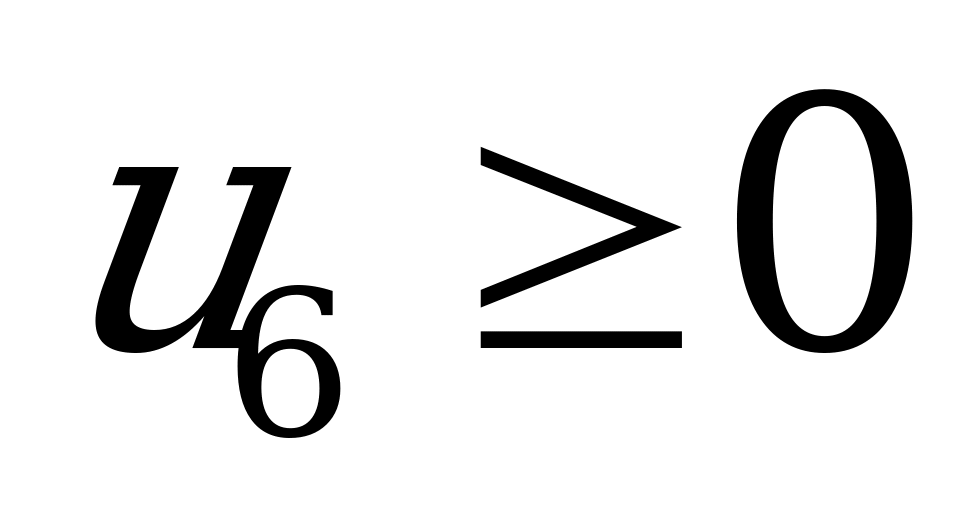 (для
(для  -задачи), преобразуем обе ЗЛП к канонической форме. При этом дополнительные переменные примем за базисные. Соответствие между переменными пары взаимно двойственных задач будет следующее:
-задачи), преобразуем обе ЗЛП к канонической форме. При этом дополнительные переменные примем за базисные. Соответствие между переменными пары взаимно двойственных задач будет следующее:
Решим, например, задачу линейного программирования, построенную для определения выигрыша игрока  . Каноническая форма задачи имеет вид:
. Каноническая форма задачи имеет вид:
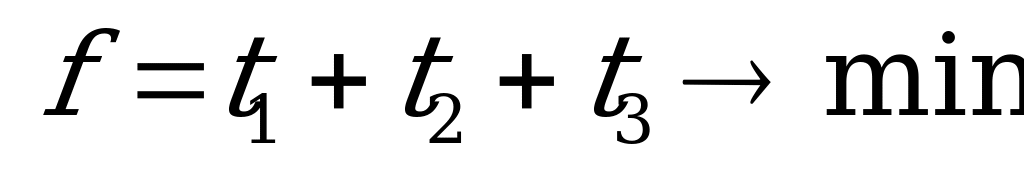
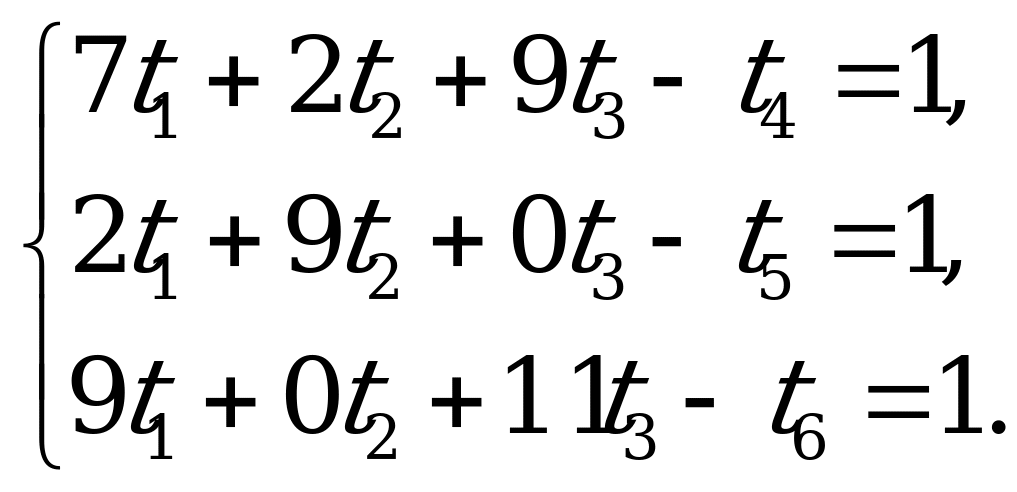
Применяем двойственный симплекс-метод:
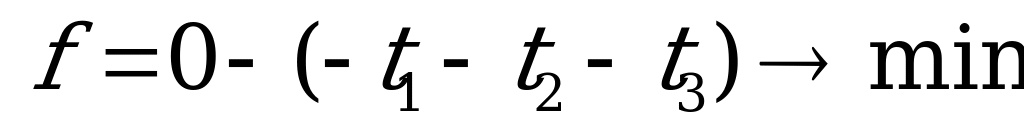
| 1 | bi | t1 | t2 | t3 | 2 | bi | t1 | t2 | t4 | 3 | bi | t1 | t5 | t4 | 4 | bi | t6 | t5 | t4 |
|
| t4 | -1 | -7 | -2 | -9 | t3 | 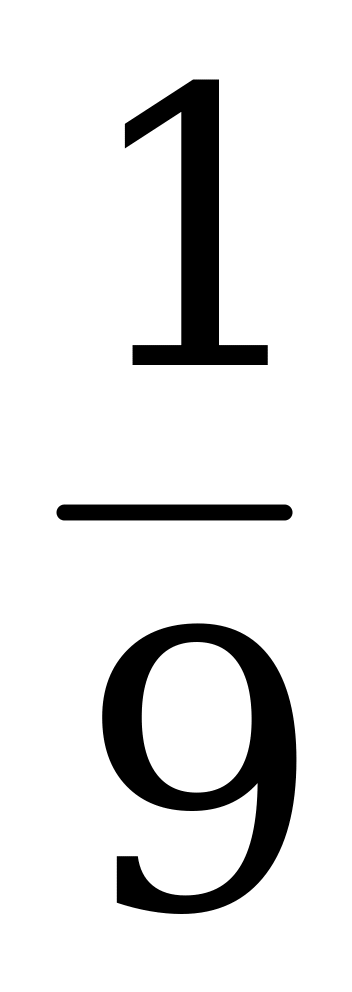
| 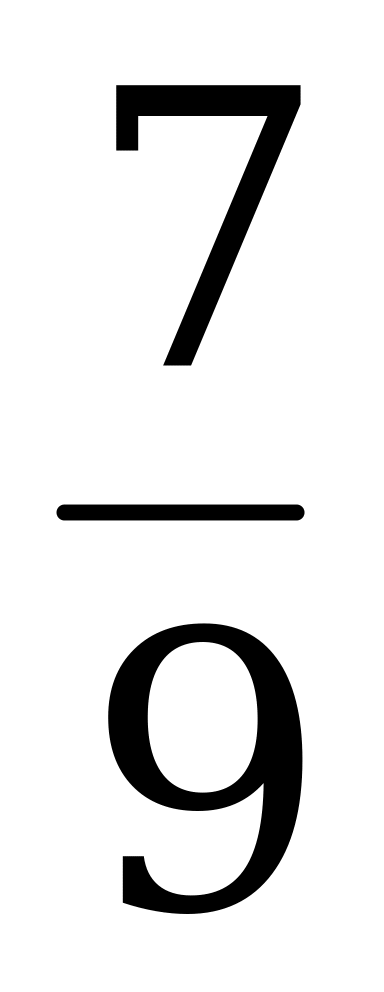
| 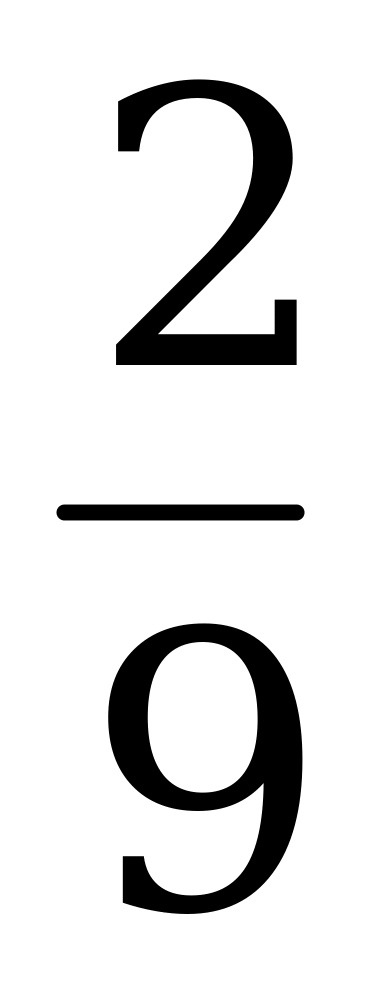
| 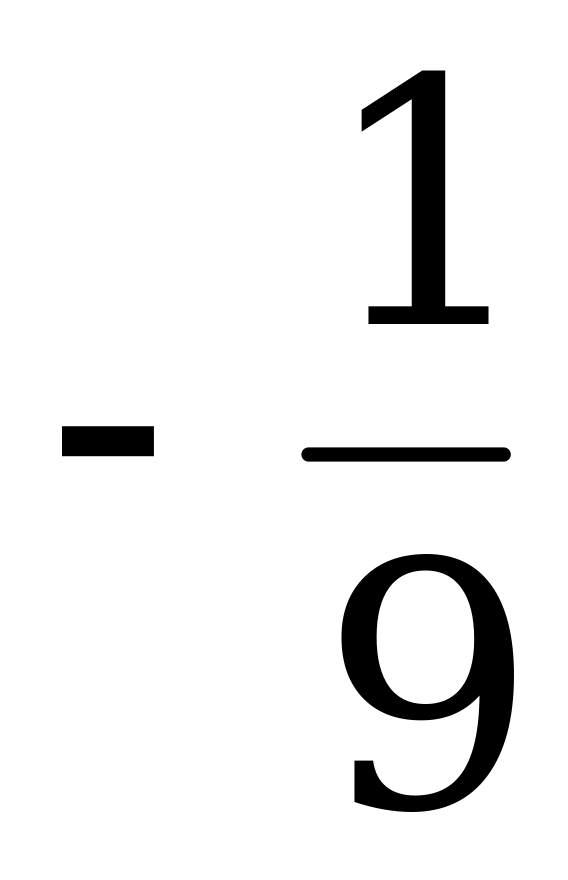
| t3 | 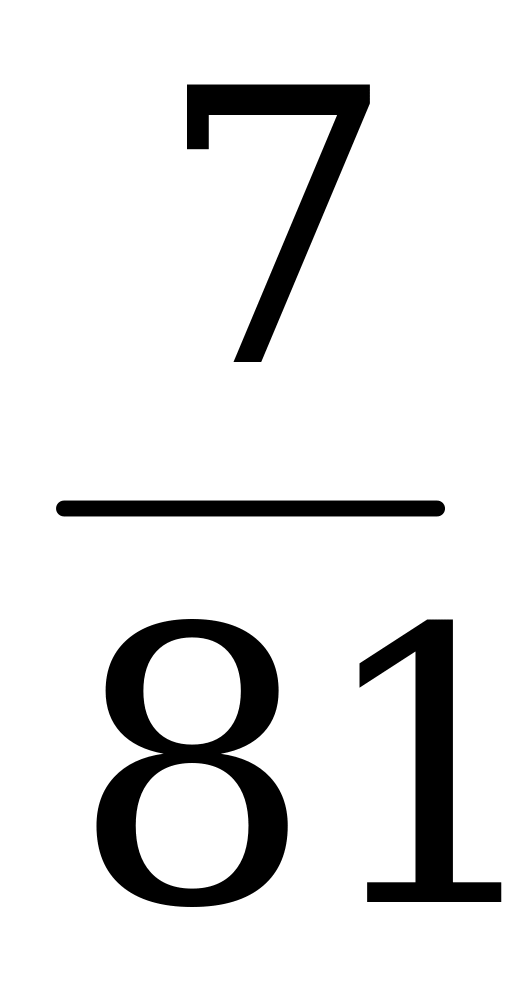
| 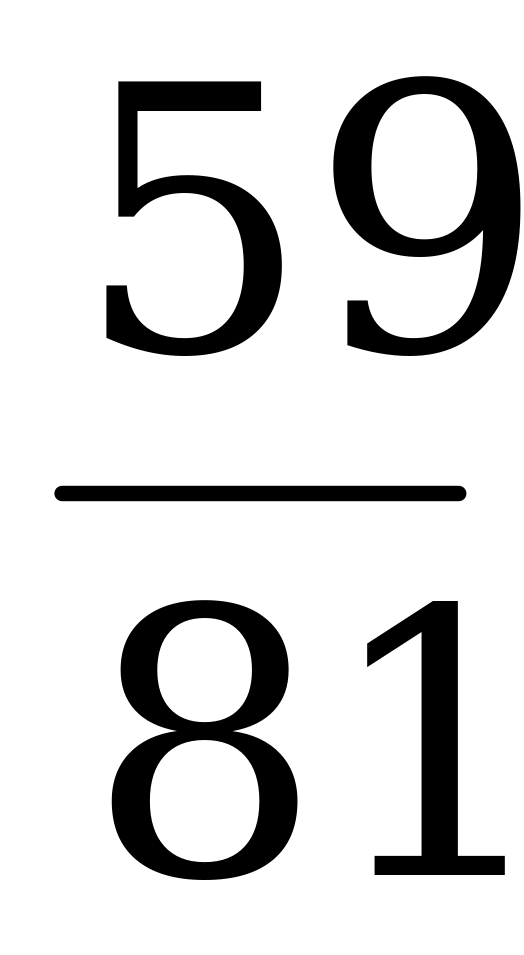
| 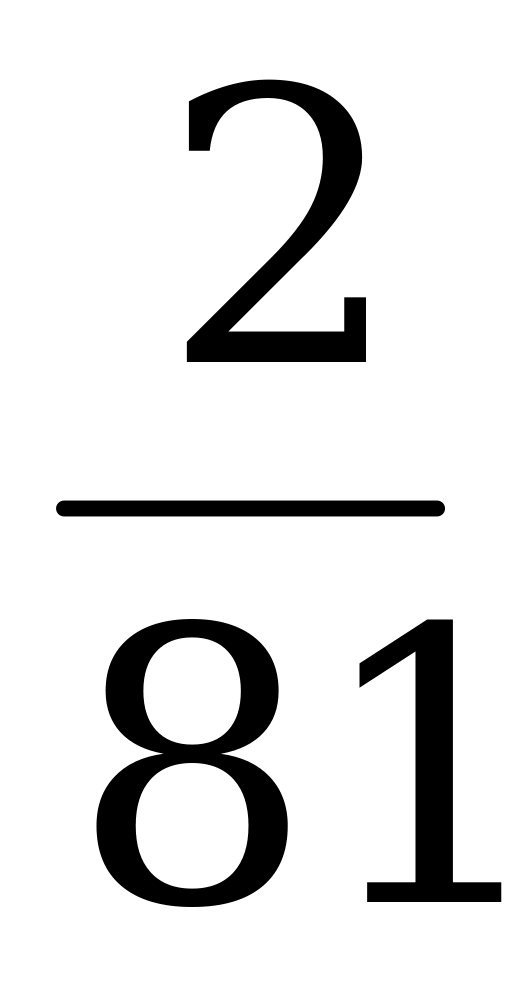
| 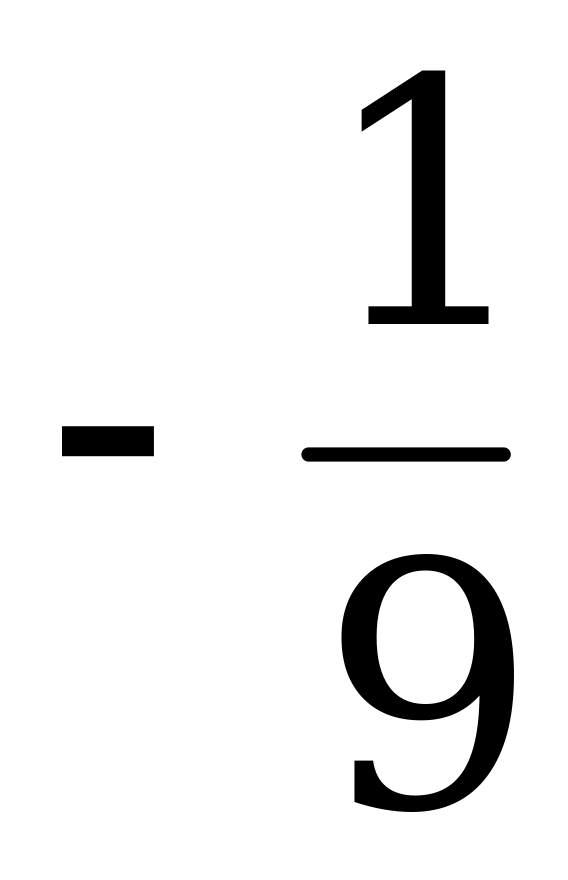
| t3 | 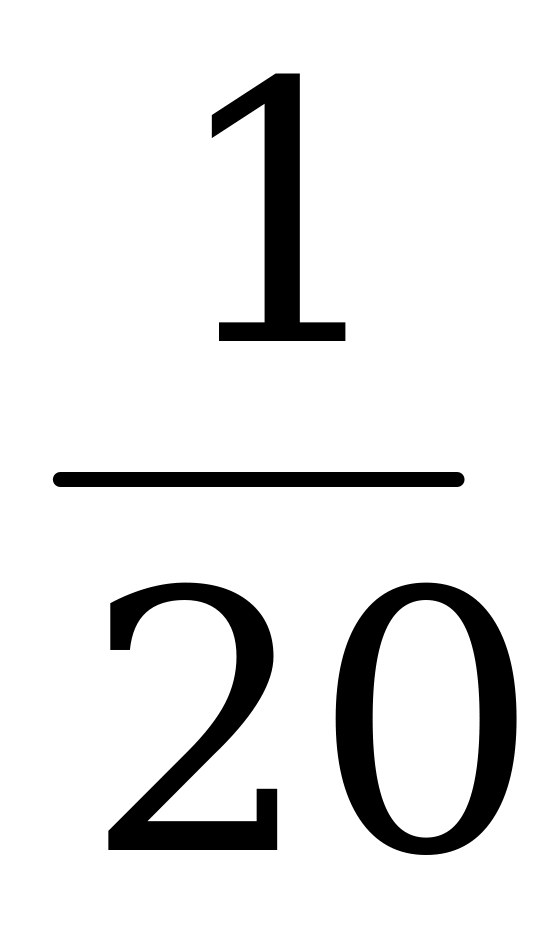
|
|
|
|
|
| t5 | -1 | -2 | -9 | 0 | t5 | -1 | -2 | -9 | 0 | t2 | 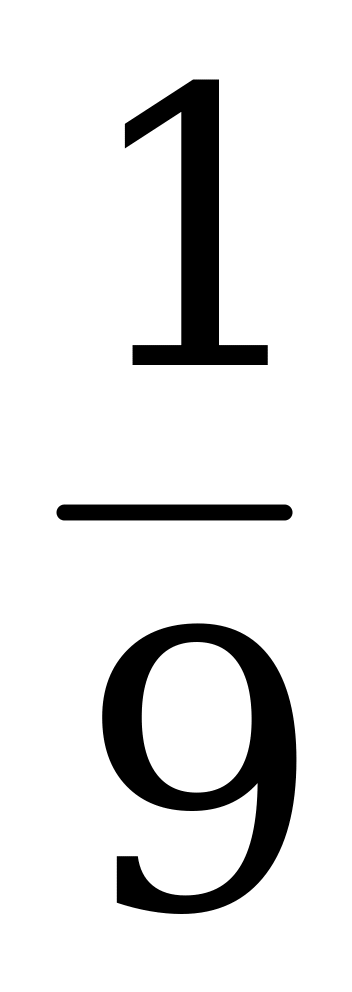
| 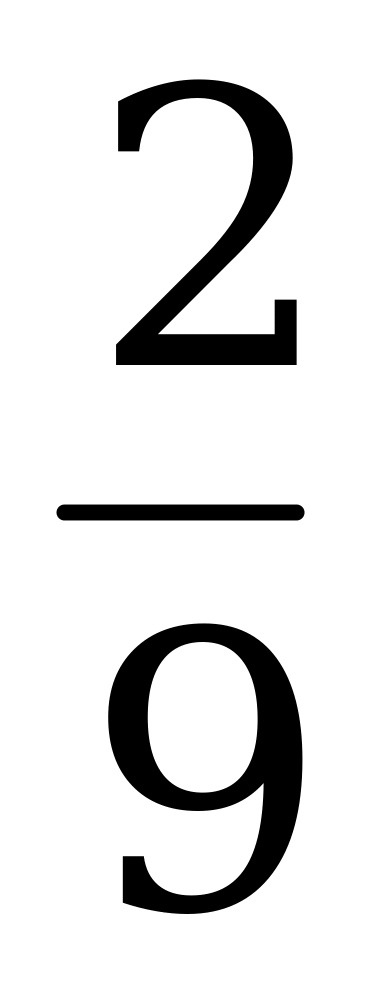
| 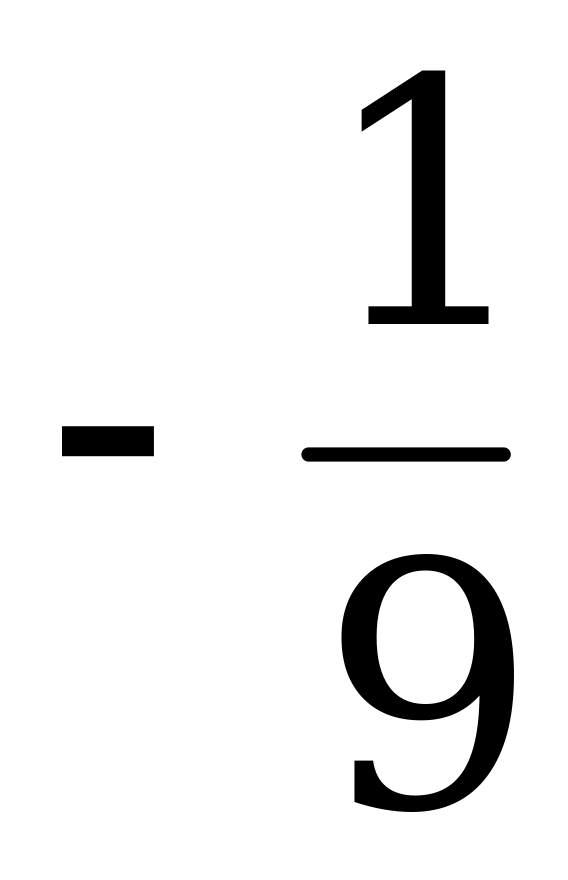
| 0 | t2 | 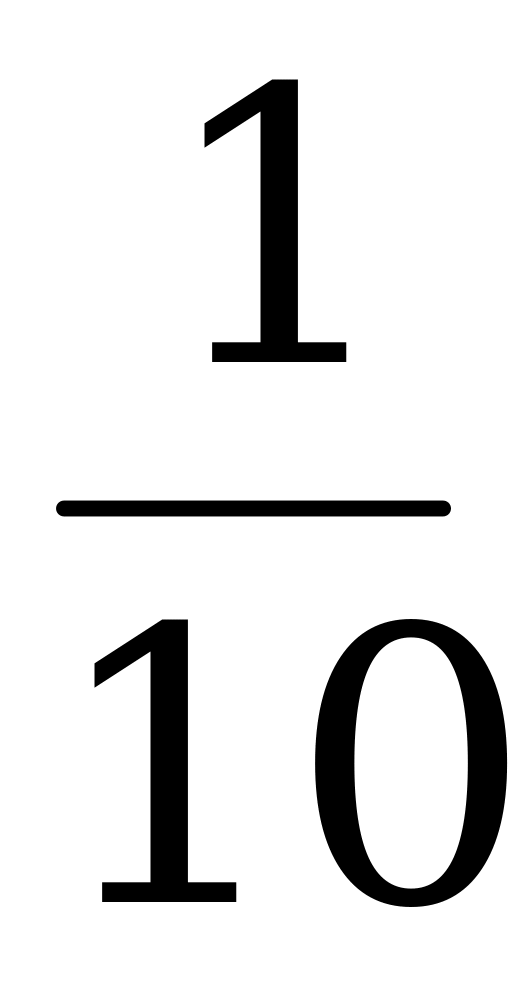
|
|
|
|
|
| t6 | -1 | -9 | 0 | -11 | t6 | 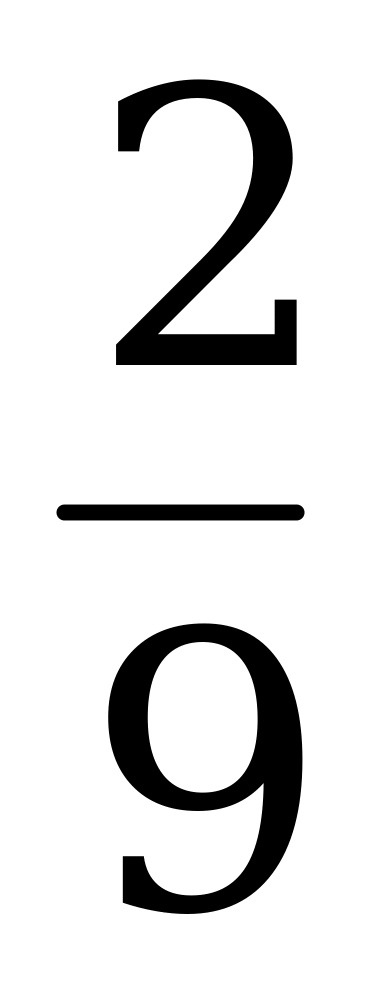
| 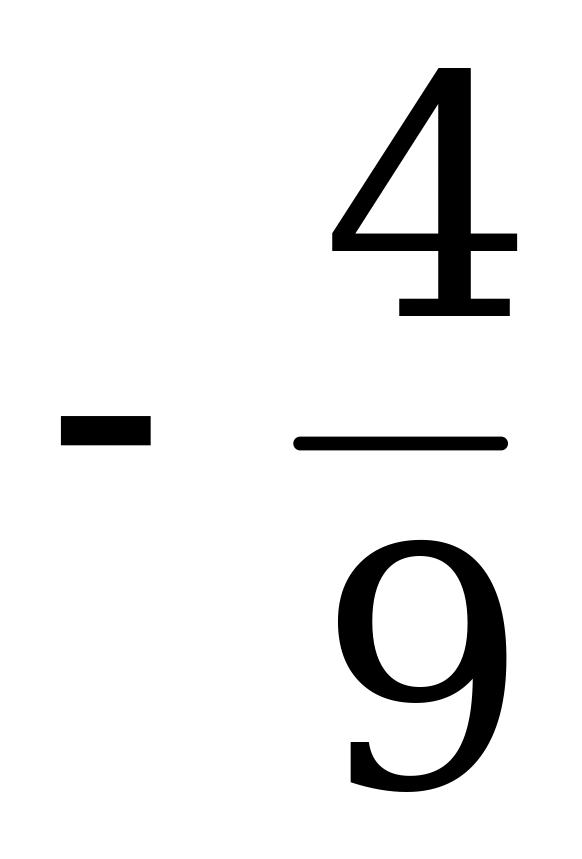
| 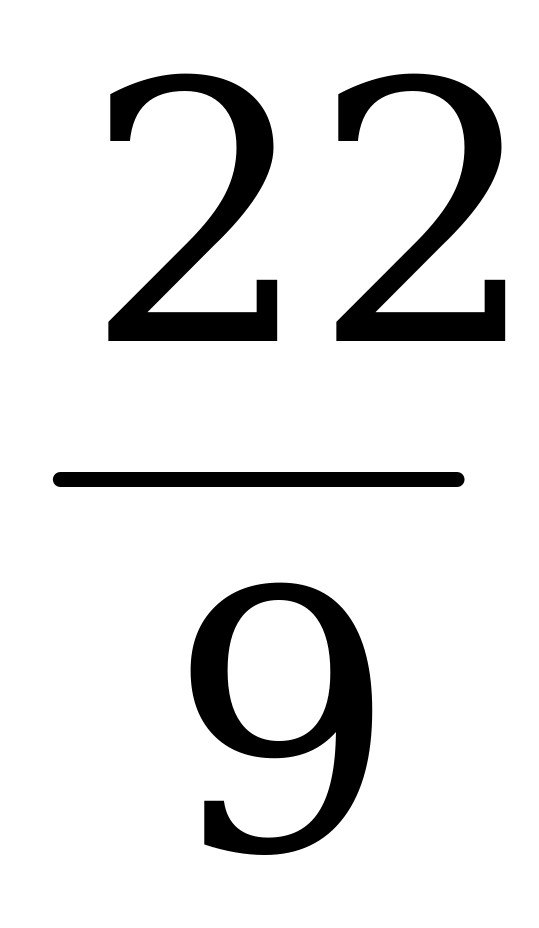
| 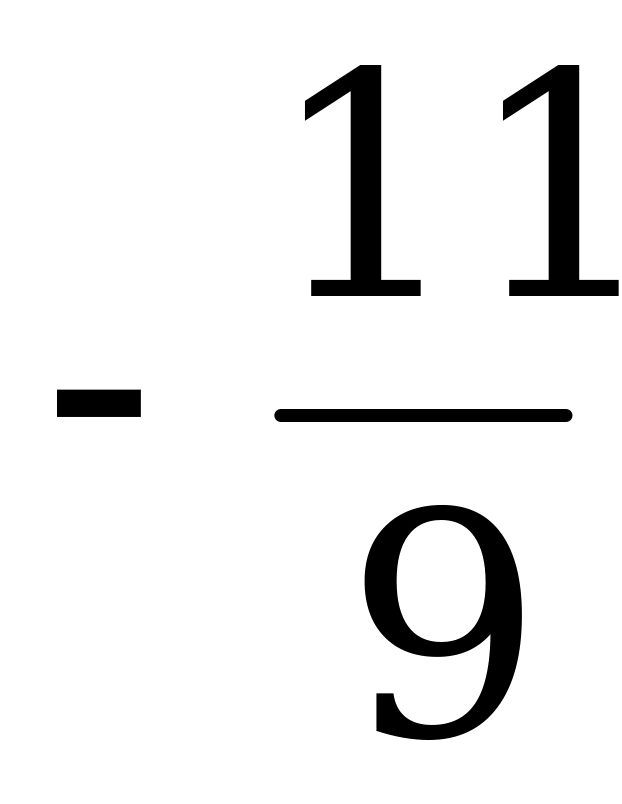
| t6 | 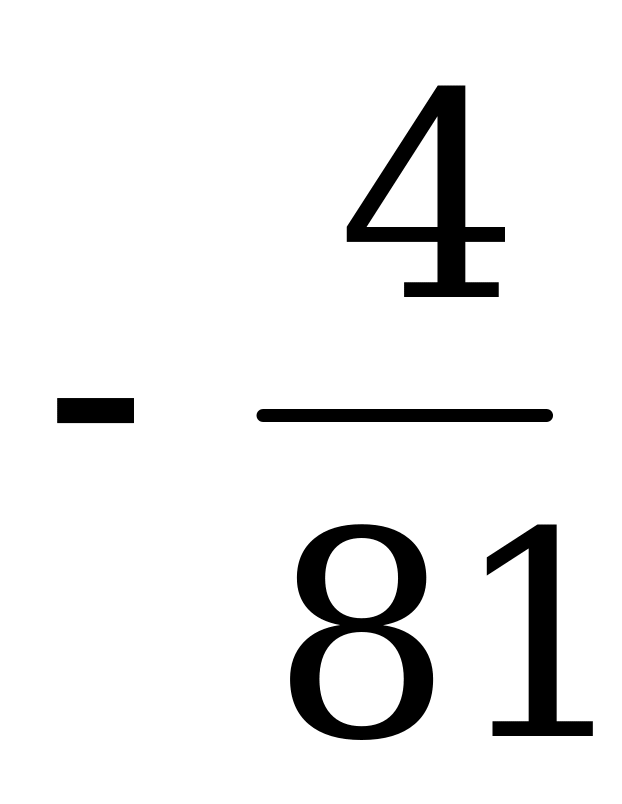
| 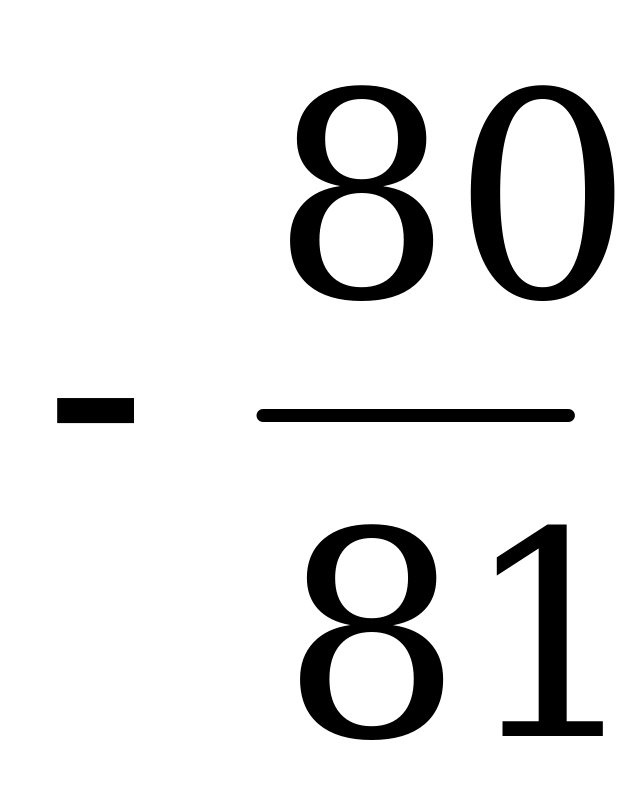
| 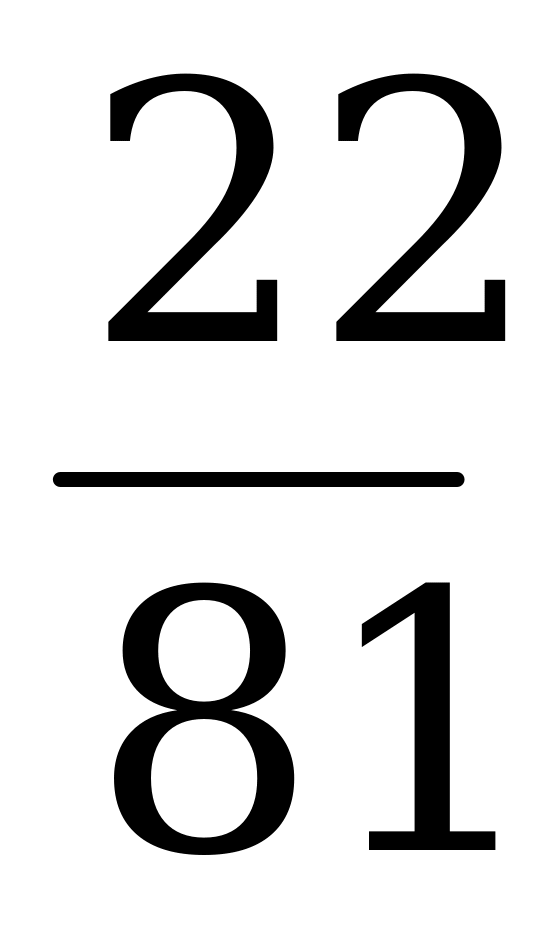
| 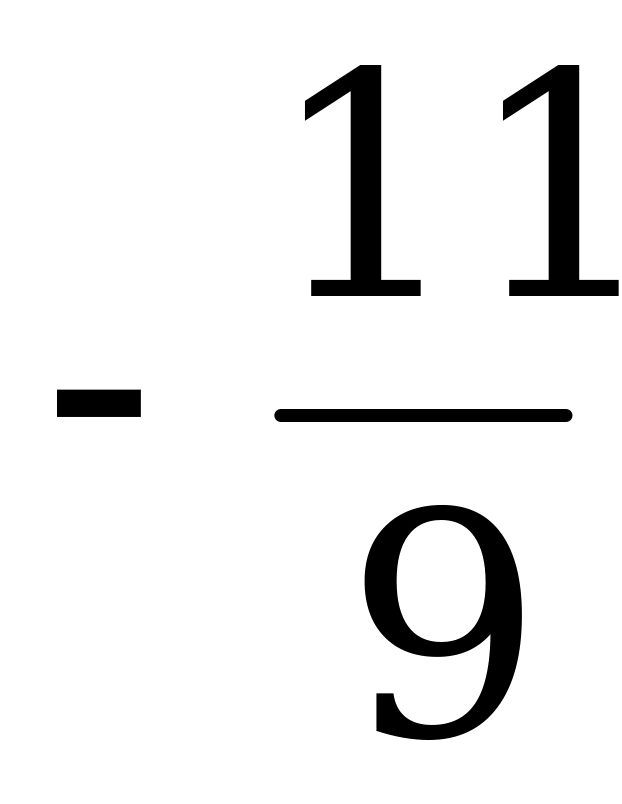
| t1 | 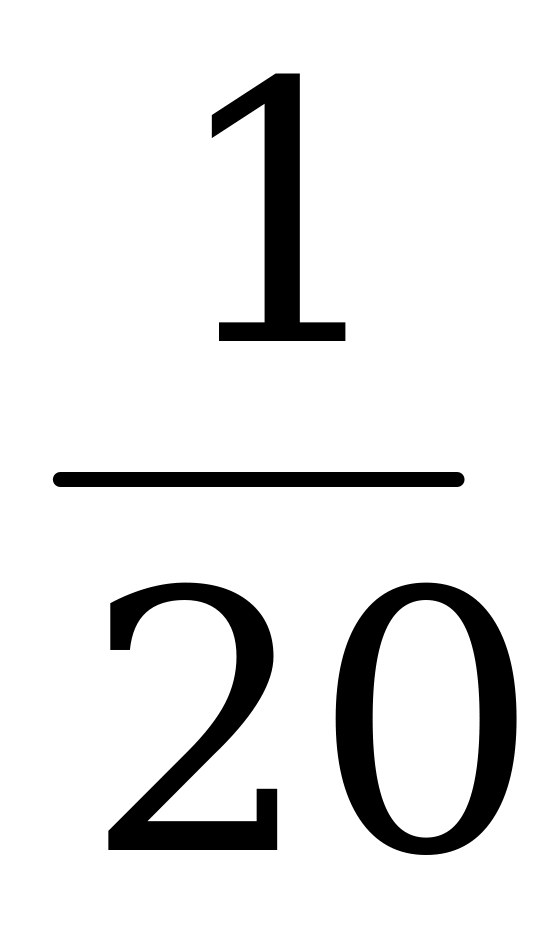
|
|
|
|
|
| f | 0 | -1 | -1 | -1 | f | 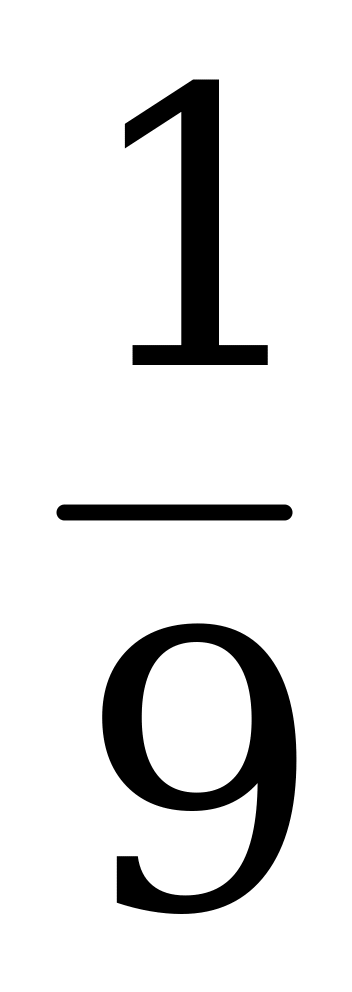
| 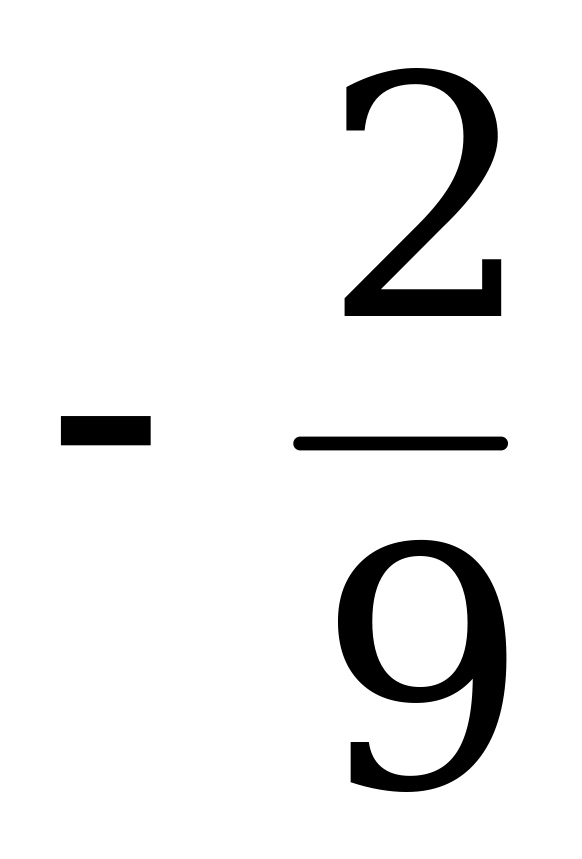
| 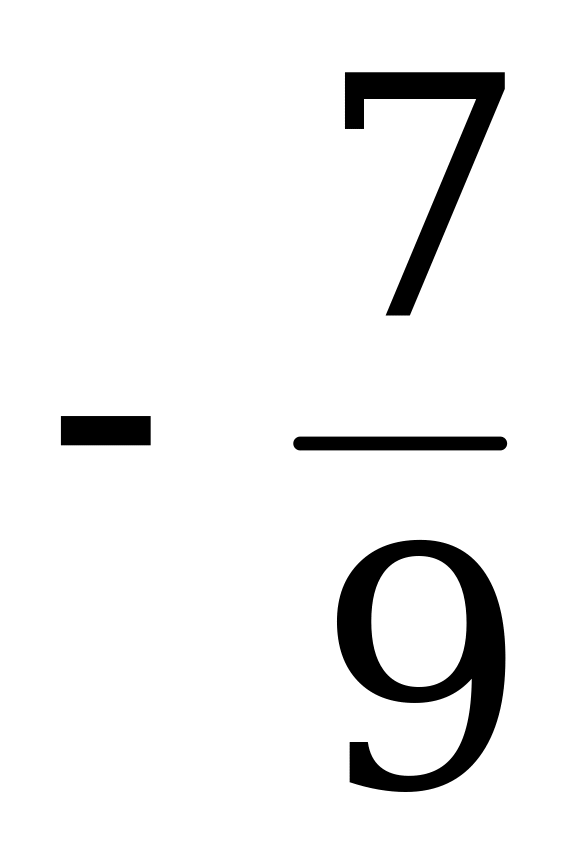
| 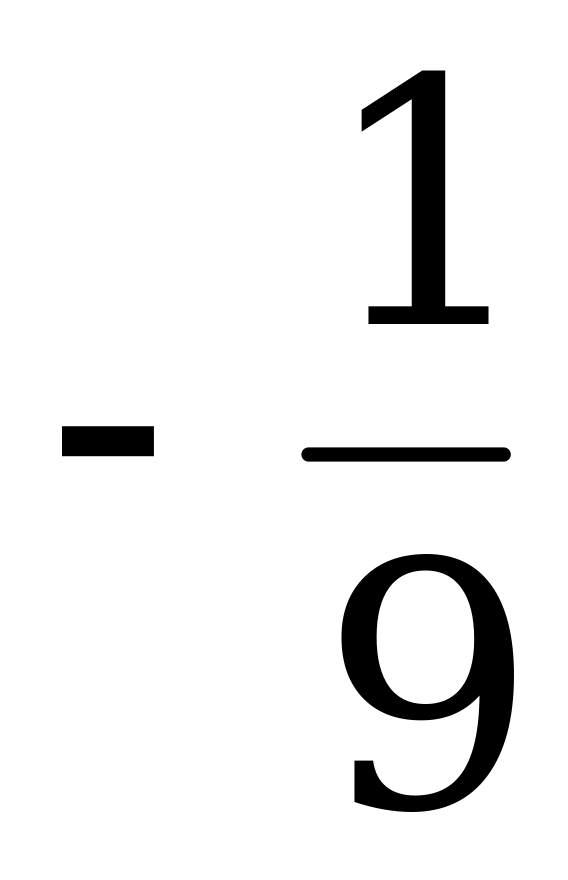
| f | 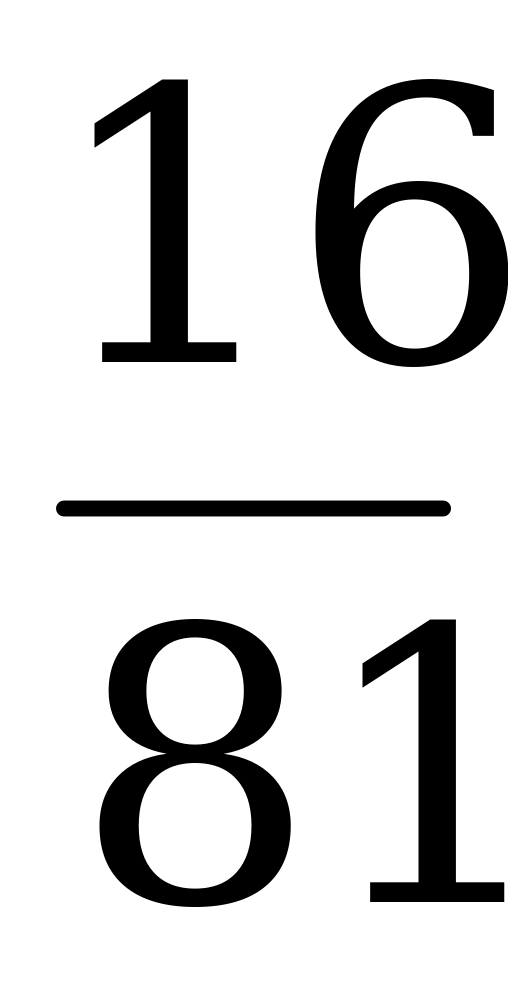
| 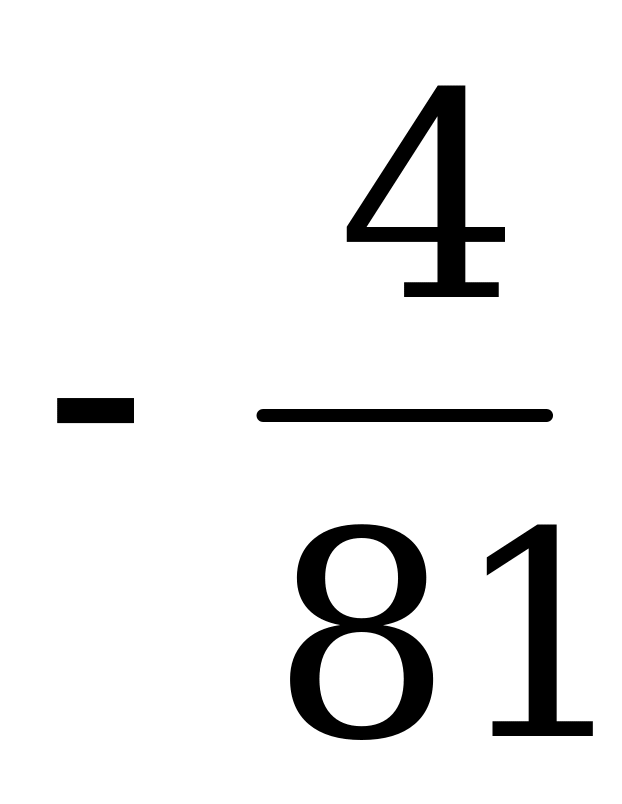
| 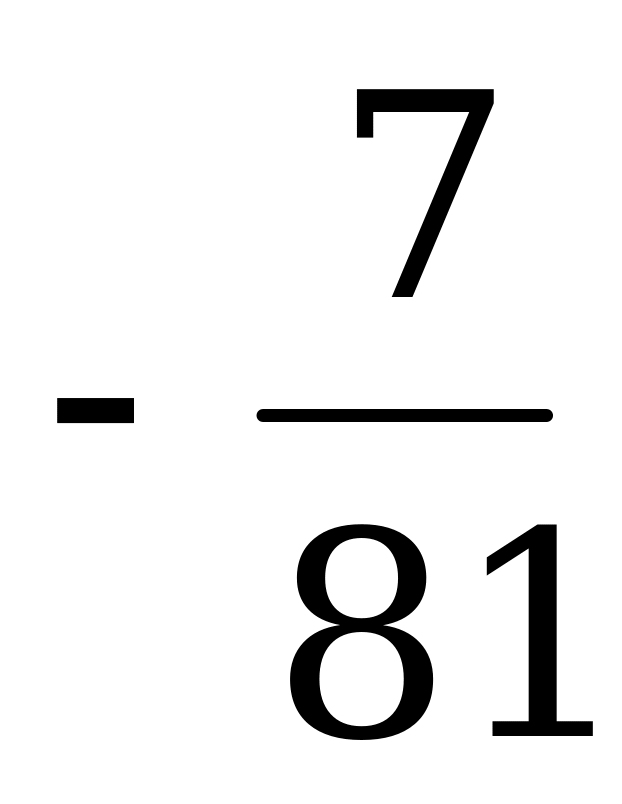
| 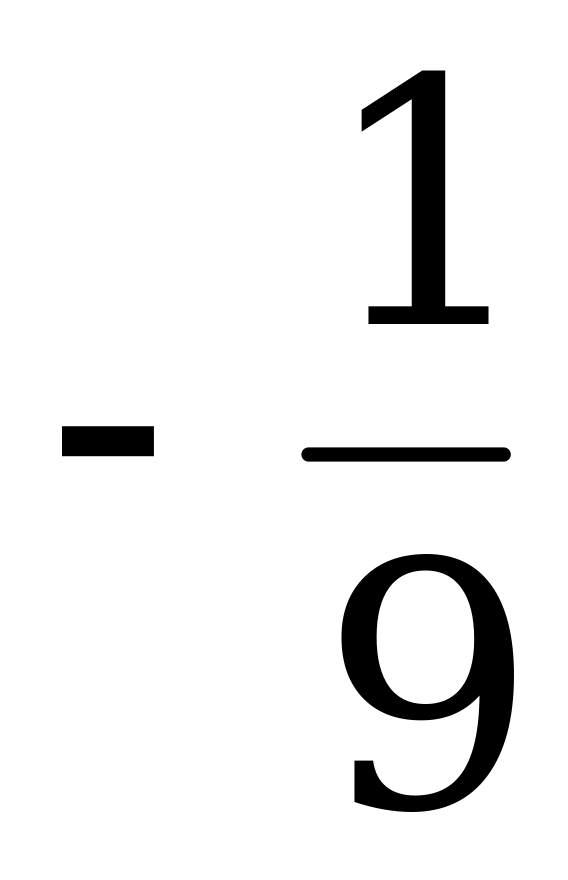
| f | 
| 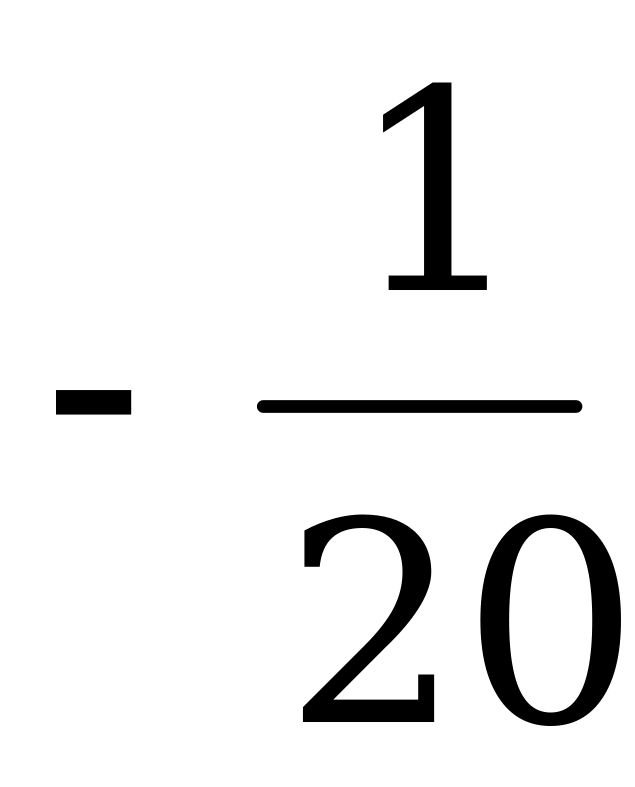
| 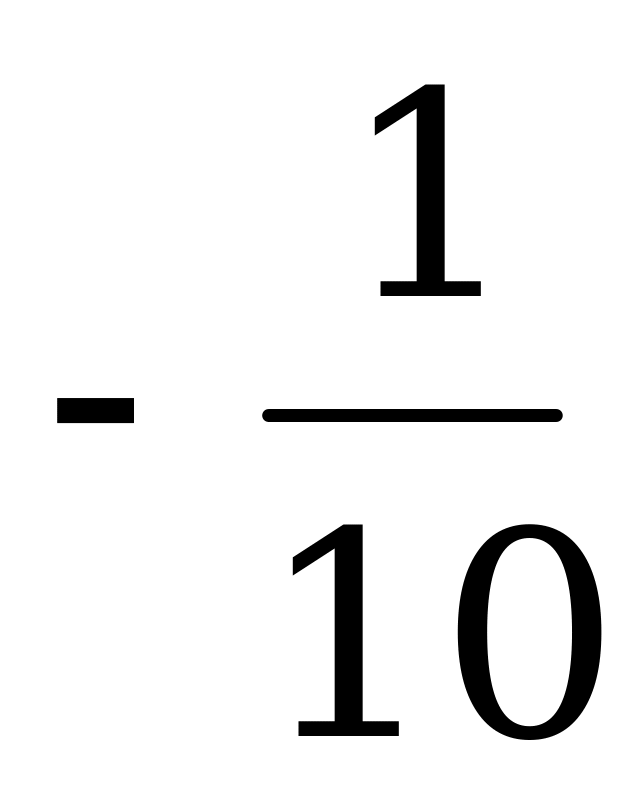
| 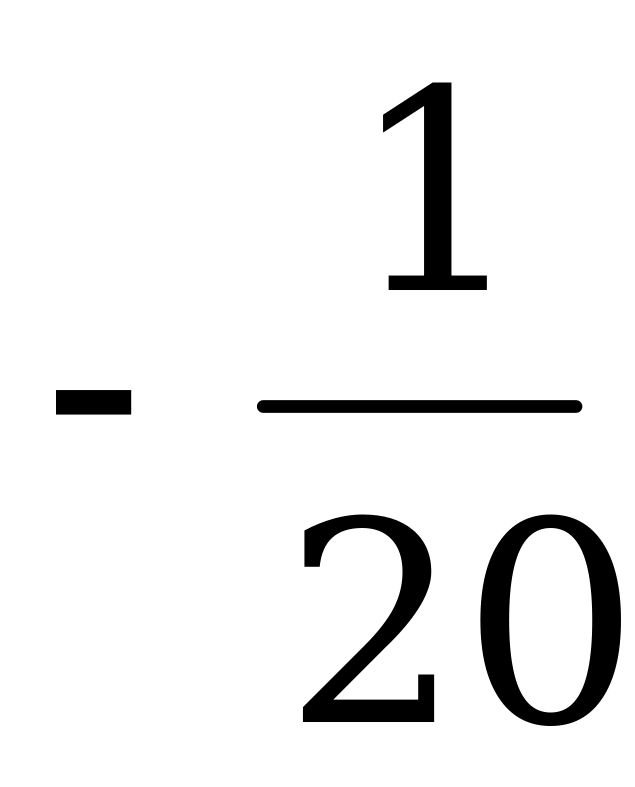
|
|
|
|
| 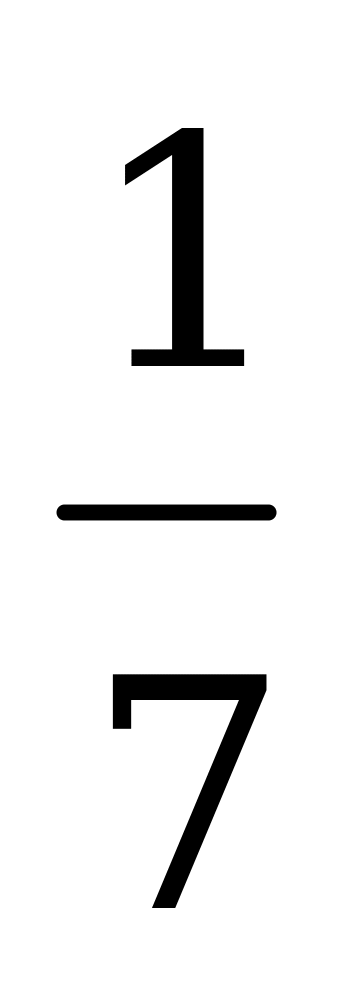
| 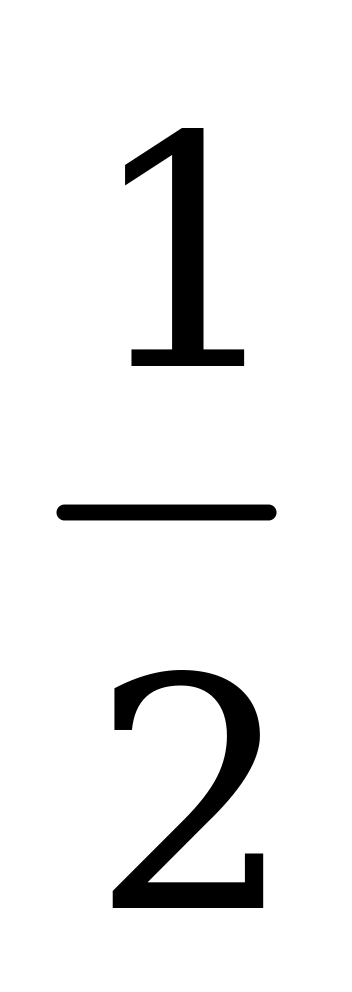
| 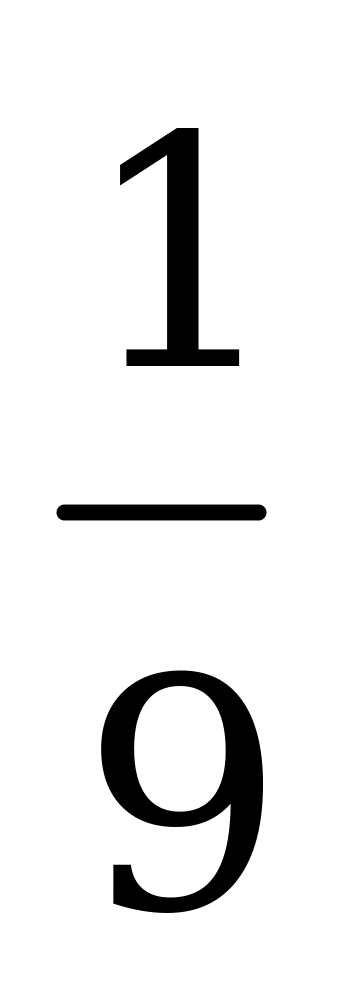
|
|
| 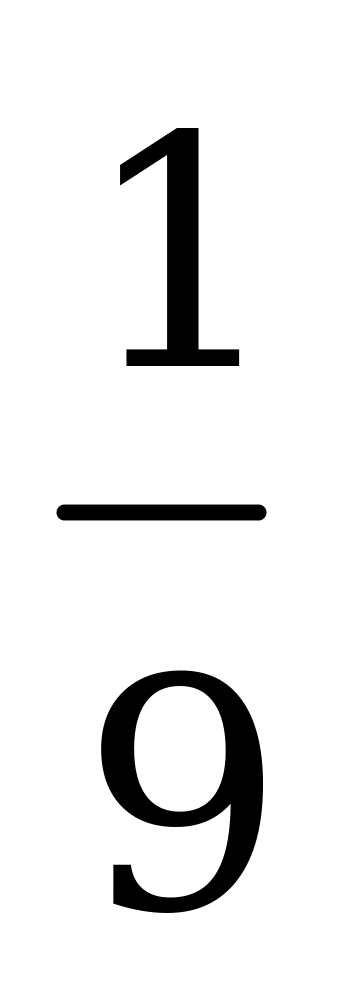
| 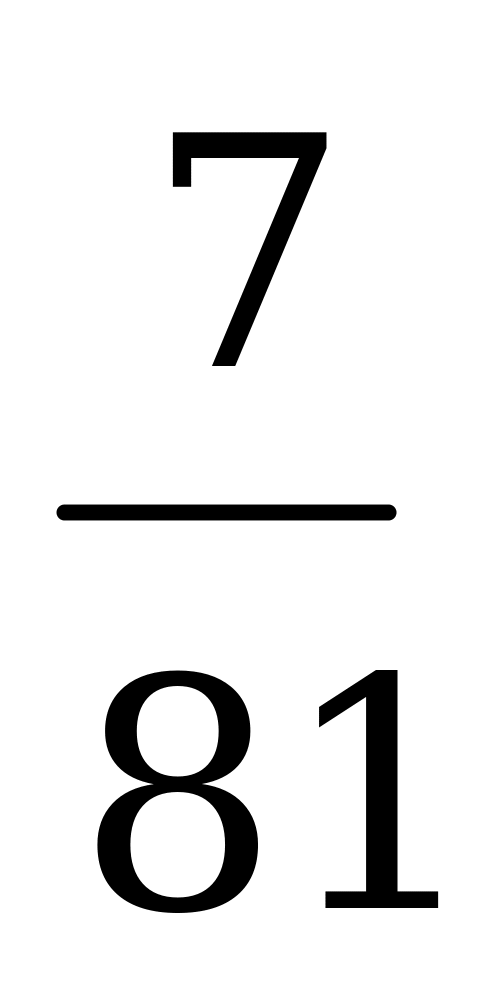
| ─ |
|
| 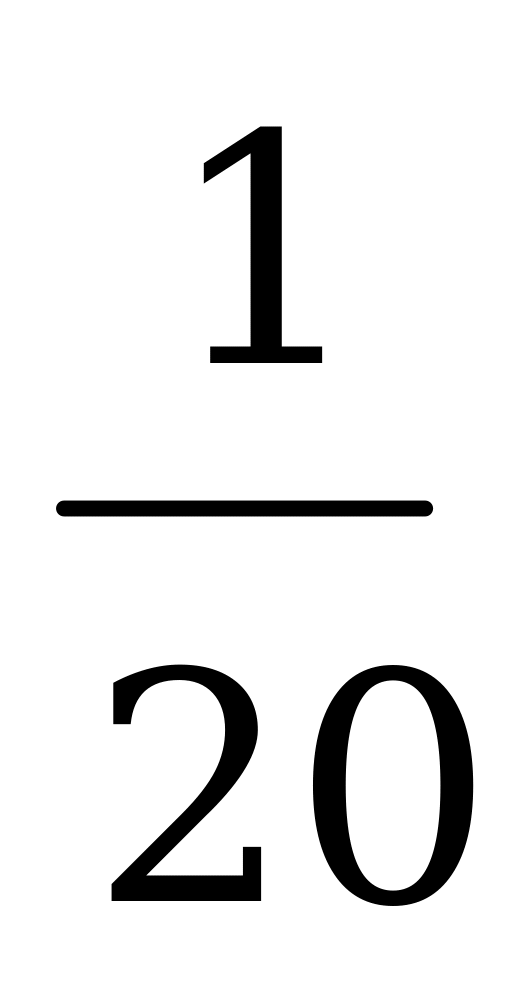
| ─ | 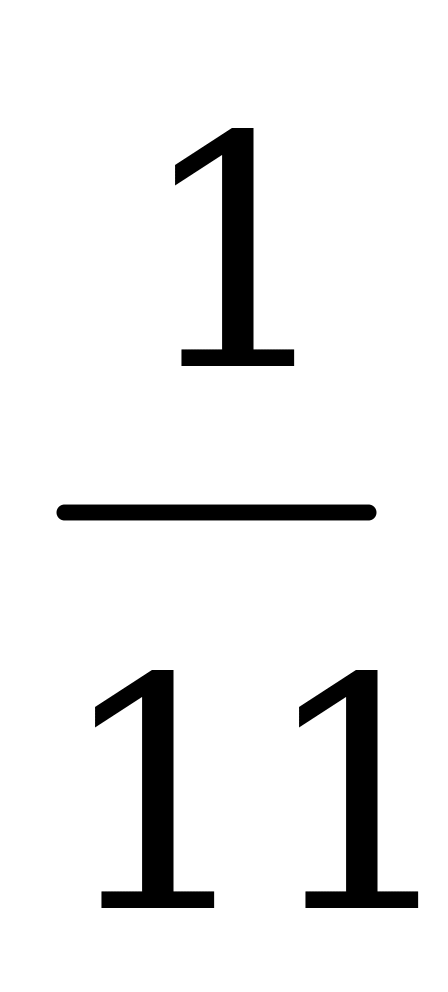
| 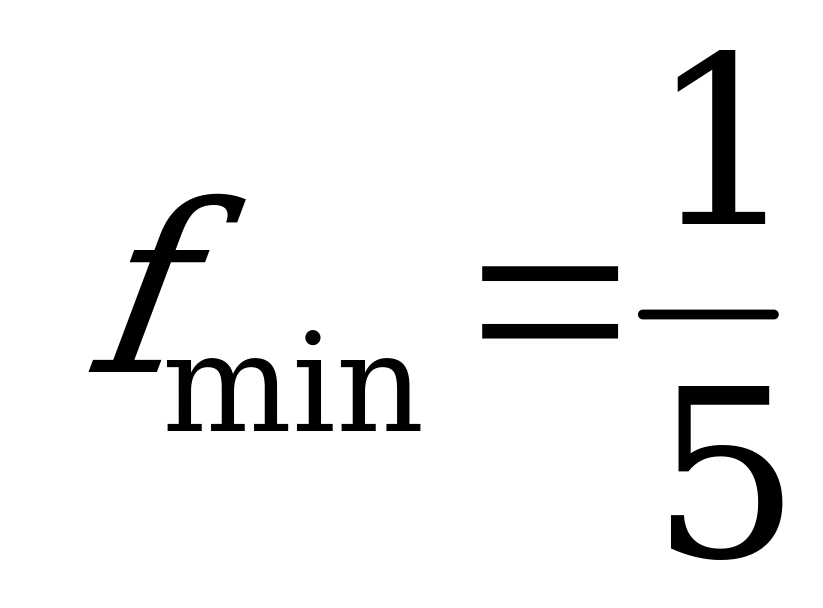
|
|
|
|
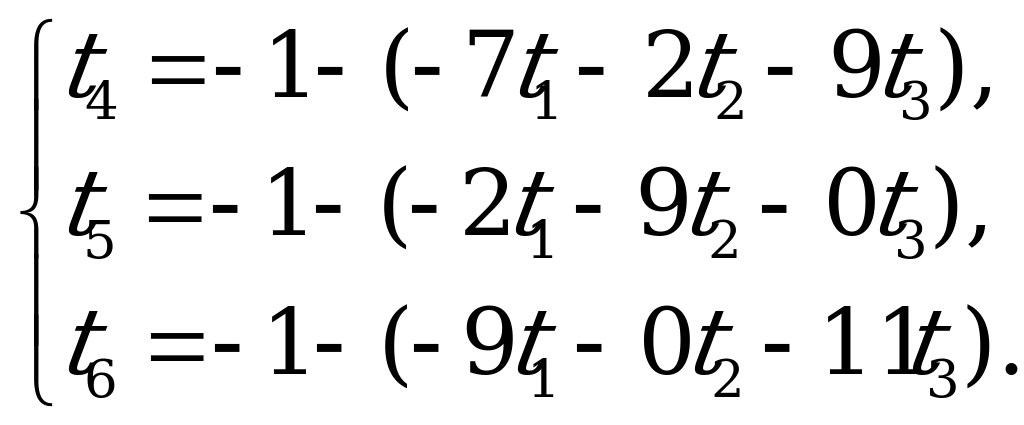
Цена игры 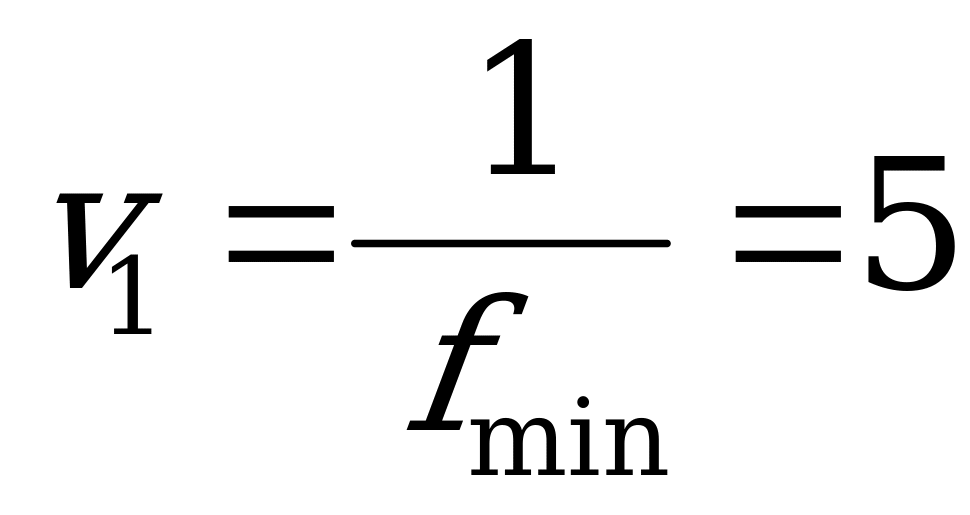 .
.
Вероятности 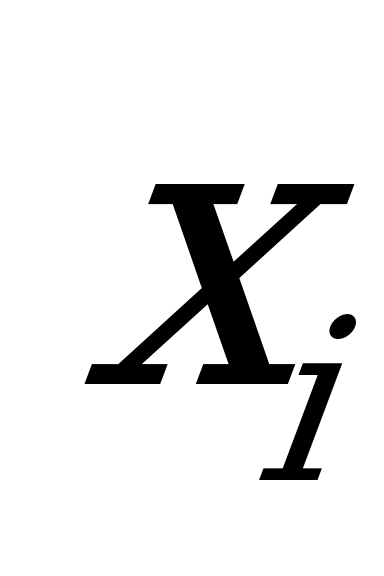 для оптимальной смешанной стратегии игрока
для оптимальной смешанной стратегии игрока  равны:
равны:
 ,
,
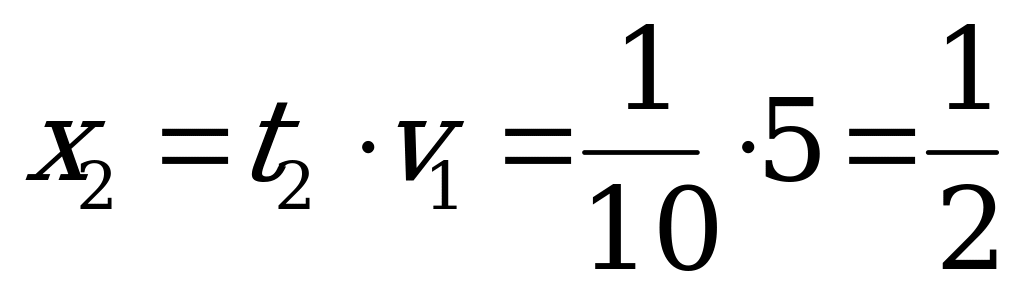 ,
,
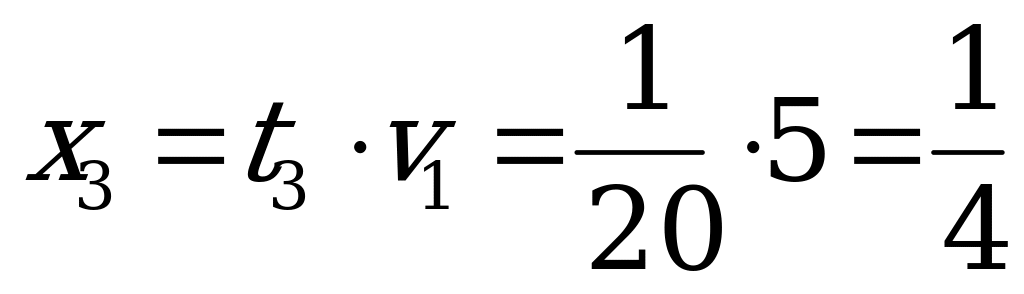 .
.
С учётом соответствия между переменными 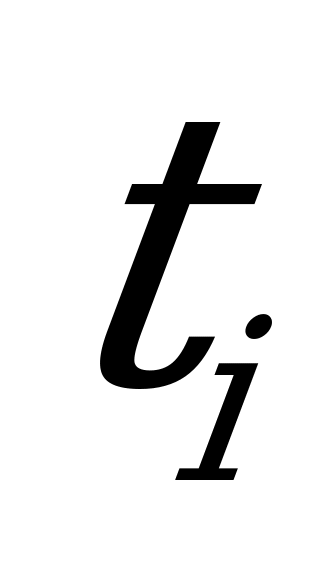 и
и  оптимальное решение
оптимальное решение  - задачи запишется следующим образом:
- задачи запишется следующим образом:
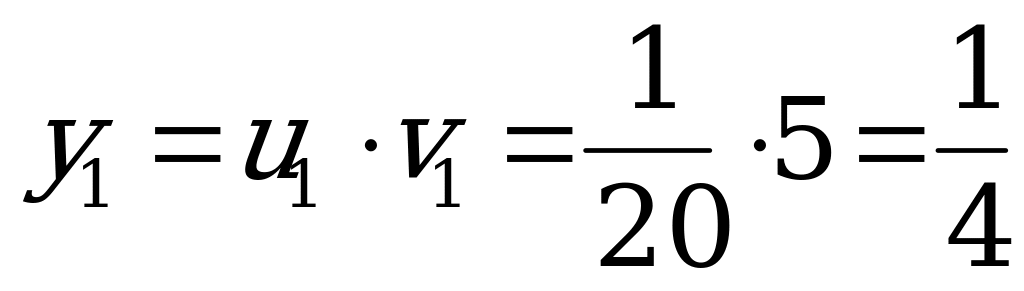 ,
,
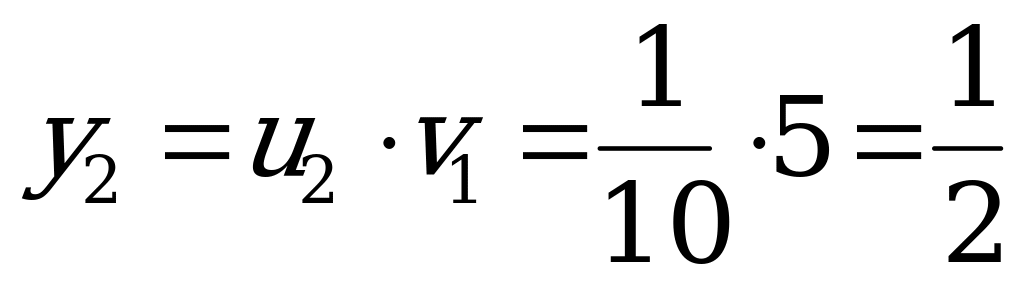 ,
,
 . Цена исходной игры
. Цена исходной игры 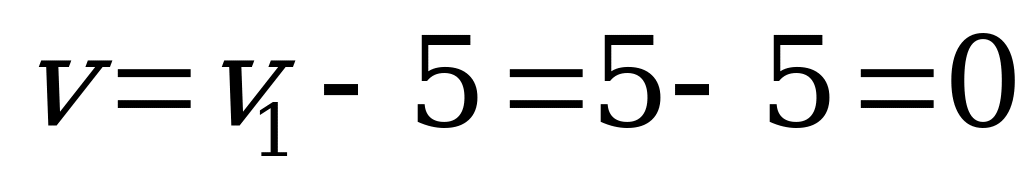 .
.
Ответ: 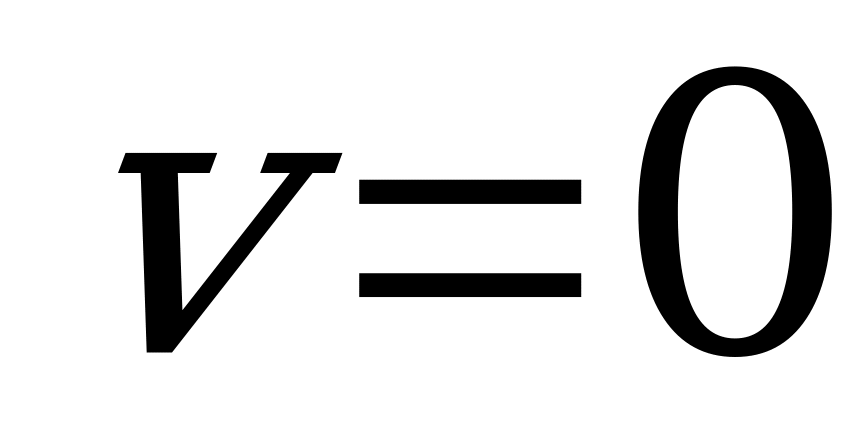 ,
, 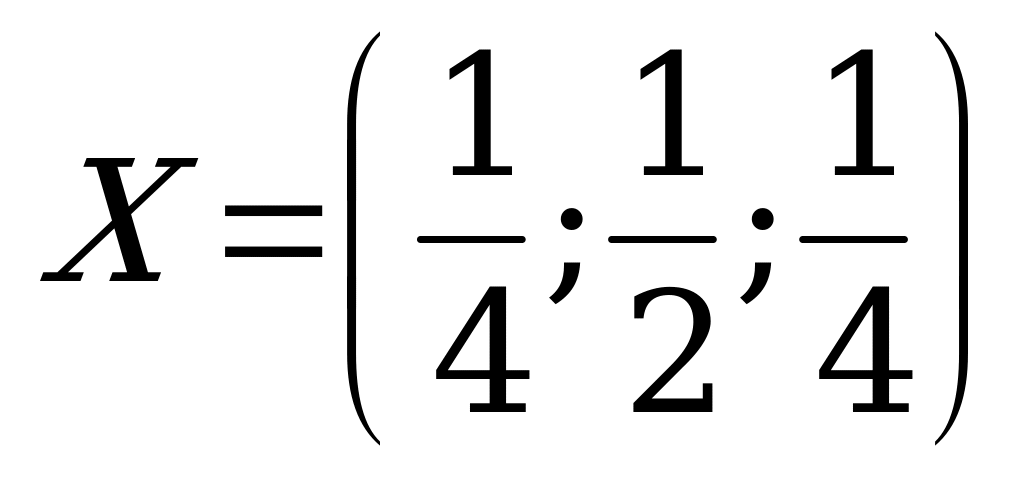 ,
, 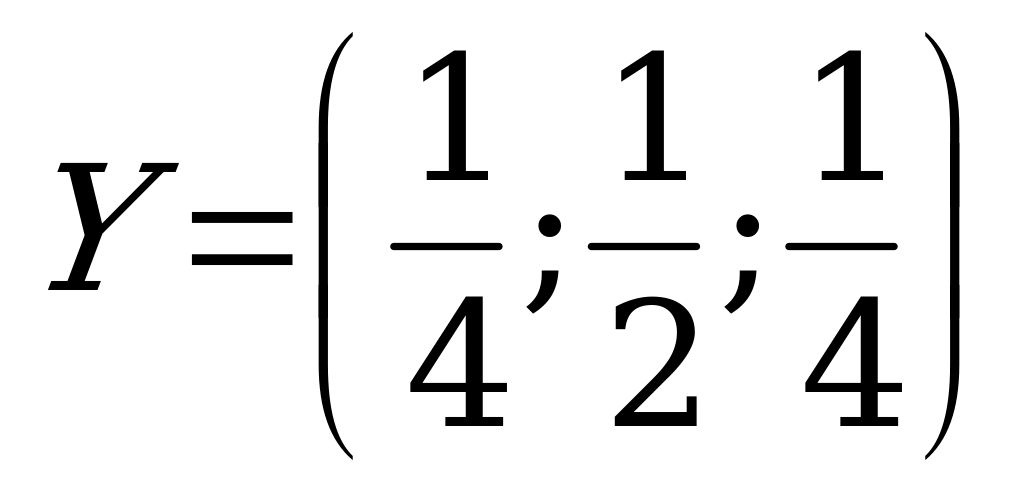 .
.
Применение смешанных стратегий мыслится таким образом: игра повторяется много раз; перед каждой партией игры, когда игроку предоставляется личный ход, он «передоверяет» свой выбор случайности, «бросает жребий», и берёт ту стратегию, которая выпала.
Пример 9-б. 
Найти решение игры, заданной матрицей: 

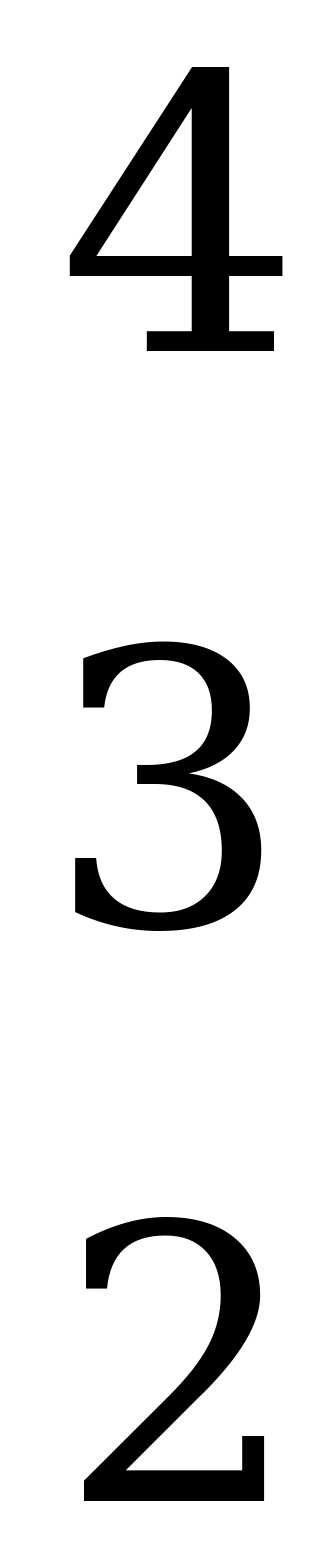
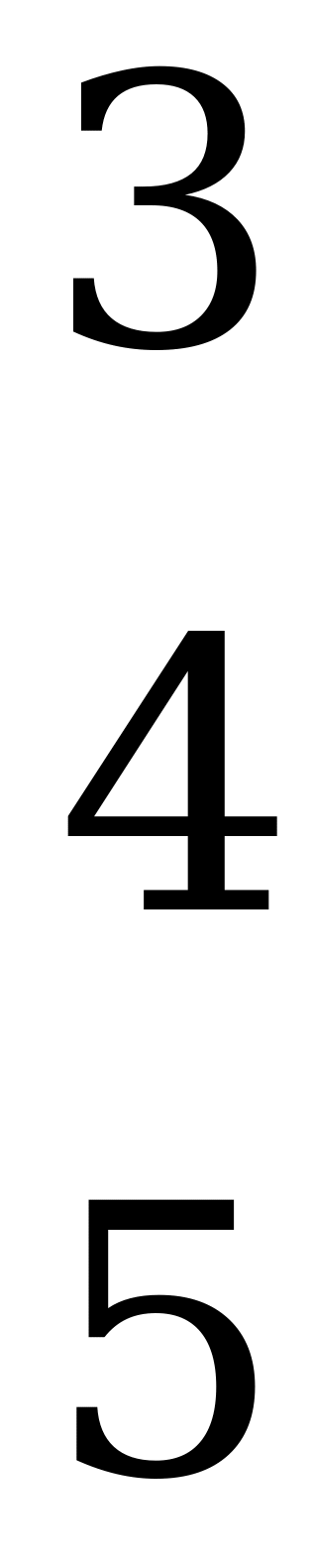
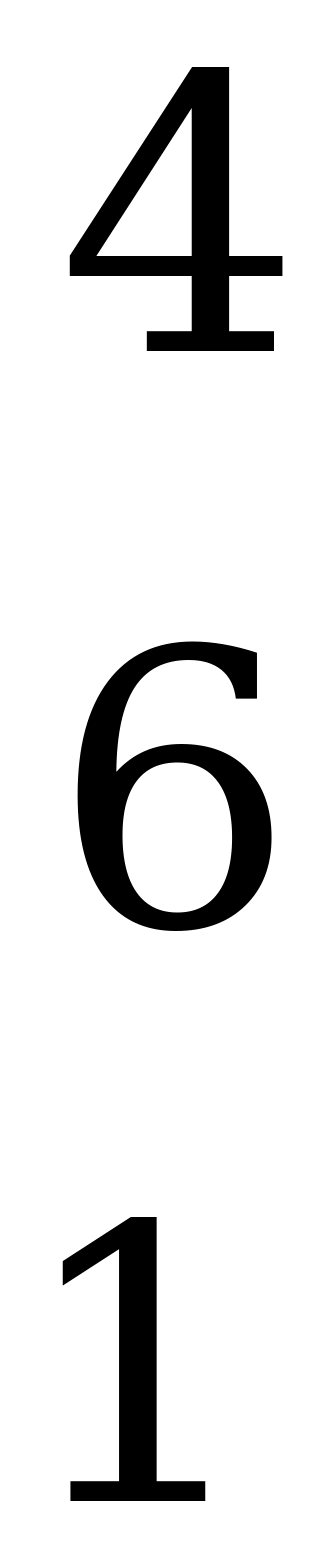
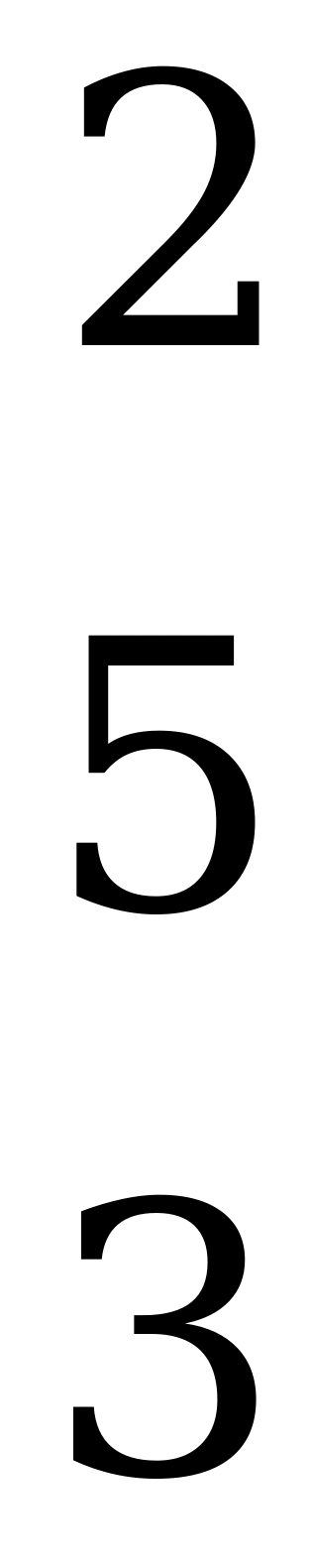
 .
.
Решение. Проверим игру на наличие седловой точки:
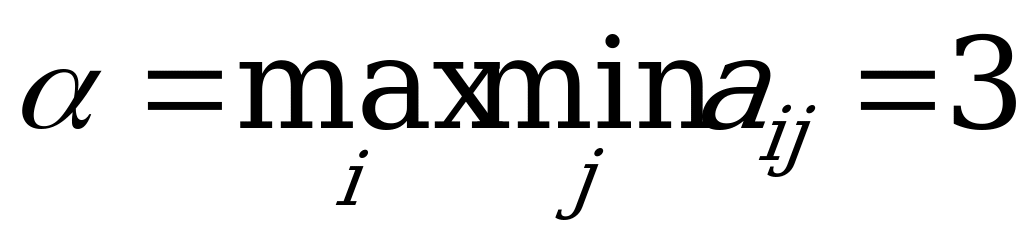 ,
, 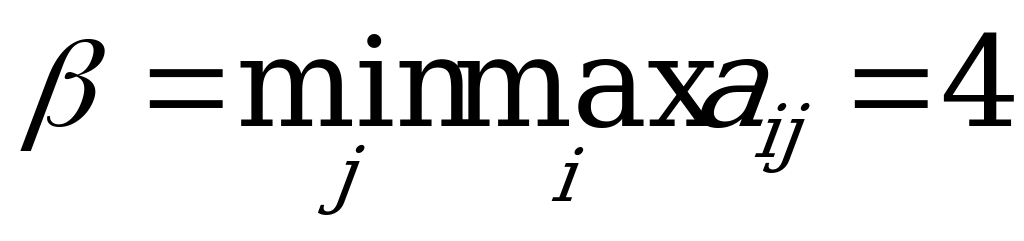 ,
, 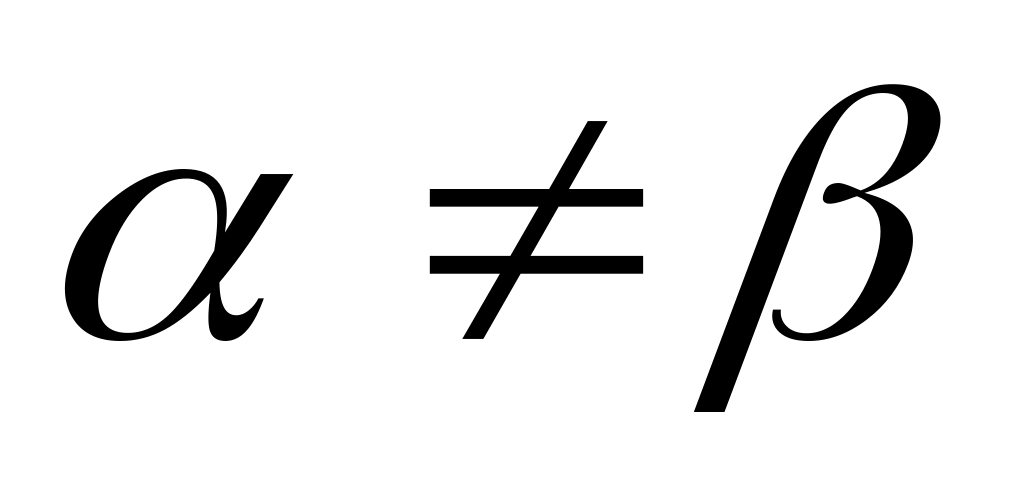 ,
,
поэтому решение игры определяем в смешанных стратегиях. Цена игры  заключена между нижней
заключена между нижней  и верхней
и верхней 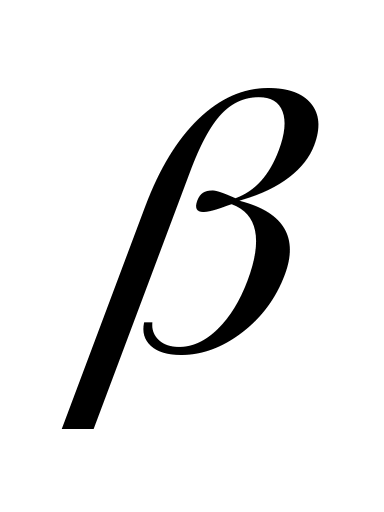 ценами, т.е.
ценами, т.е. 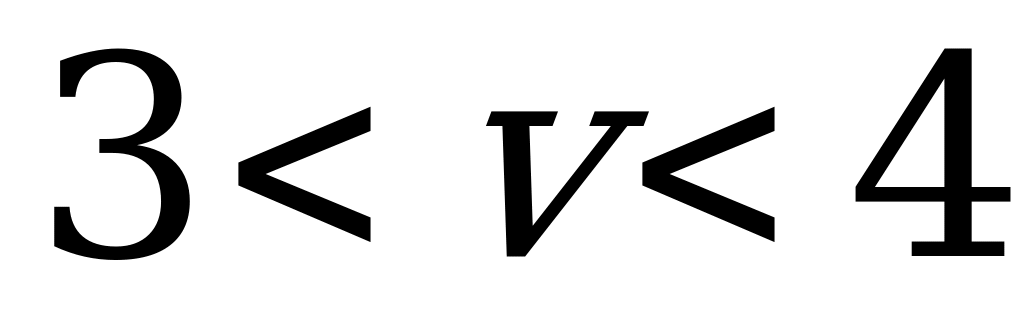 .
.
Для определения оптимальной стратегии игрока А составим следующую задачу линейного программирования: найти минимальное значение функции 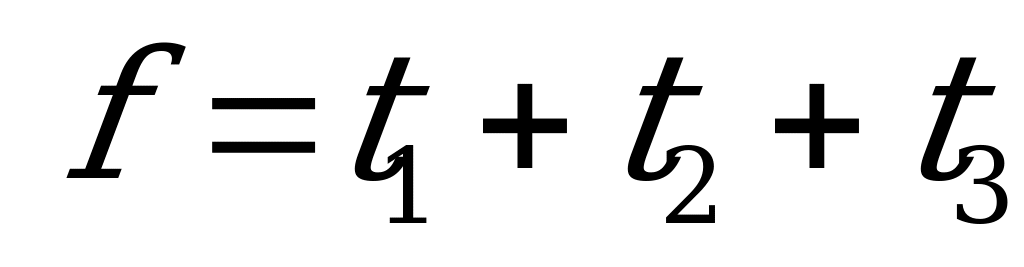
при ограничениях 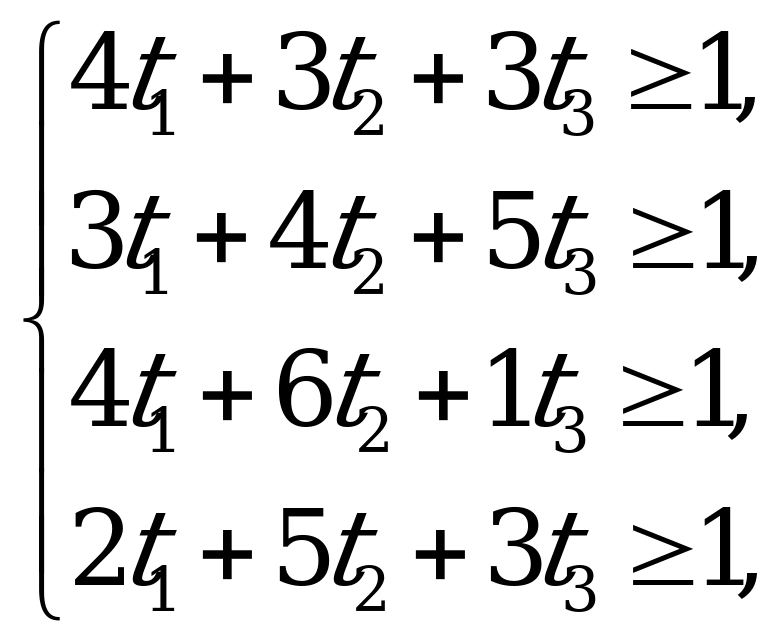
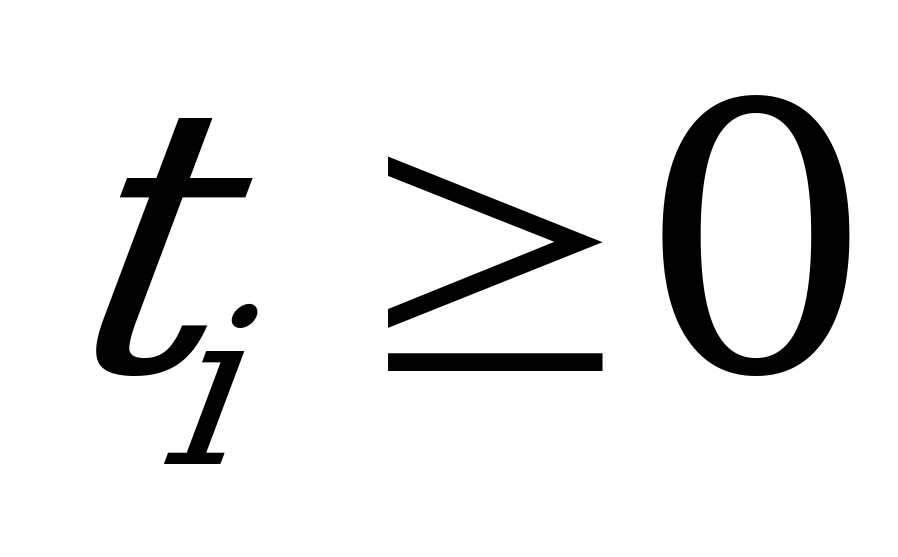
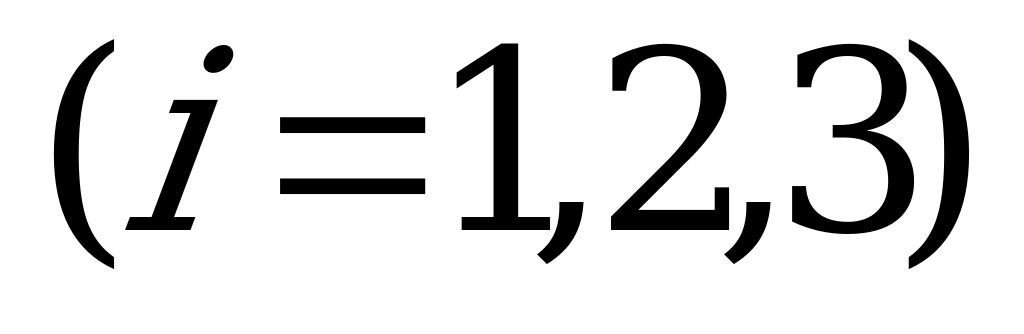 .
.
Двойственная задача для определения оптимальной стратегии игрока В формулируется так: найти максимум функции 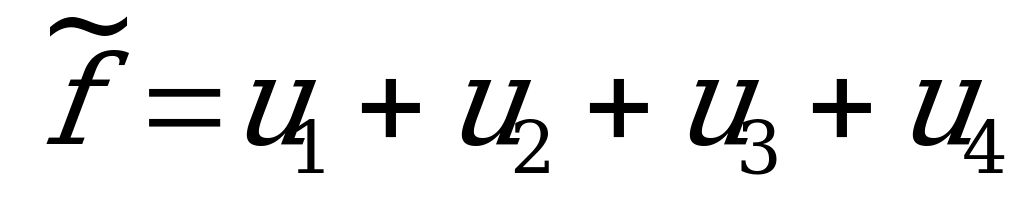
при ограничениях 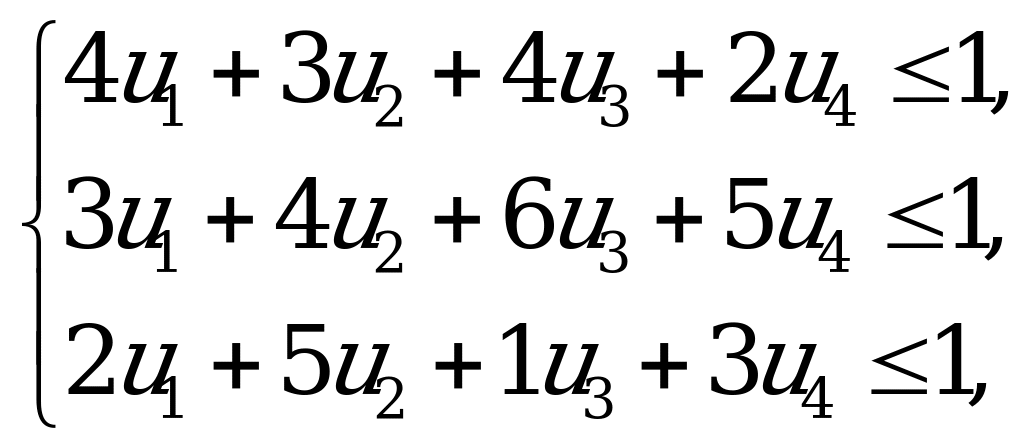
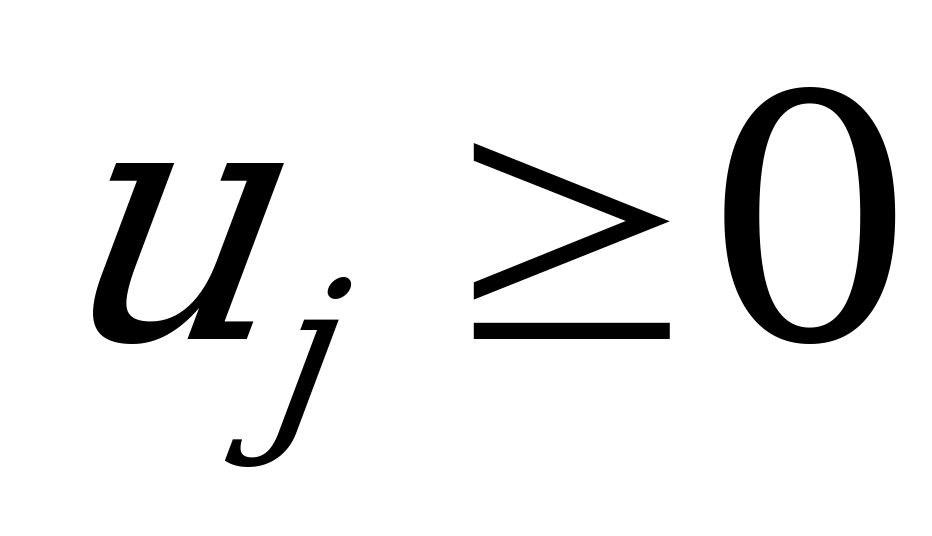
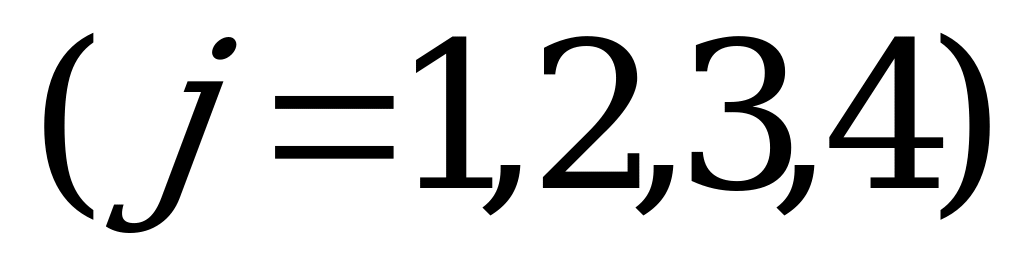 .
.

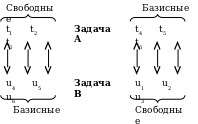
Свободные
Базисные
u5 u6 u7


Задача А
Задача В


t1 t2 t3

t4 t5 t6 t7







u1 u2 u3 u4
Базисные
Свободные
Решим, например, задачу линейного программирования, построенную для определения выигрыша игрока  . Каноническая форма задачи имеет вид:
. Каноническая форма задачи имеет вид:
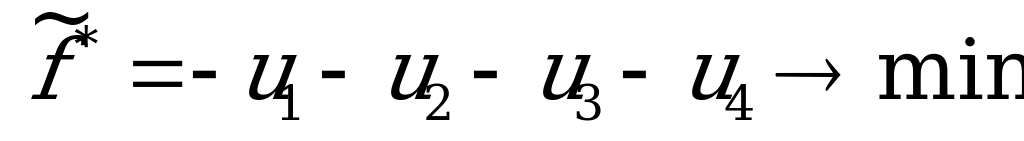
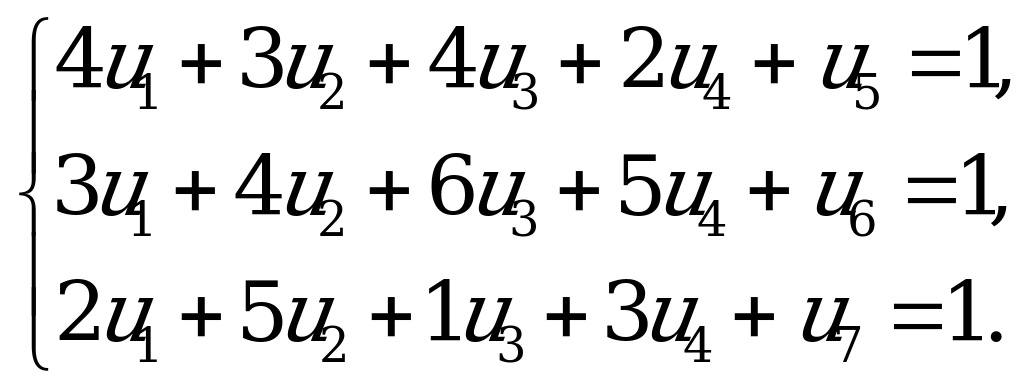
Применяем симплекс-метод:
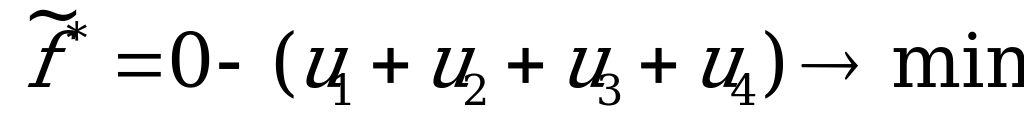
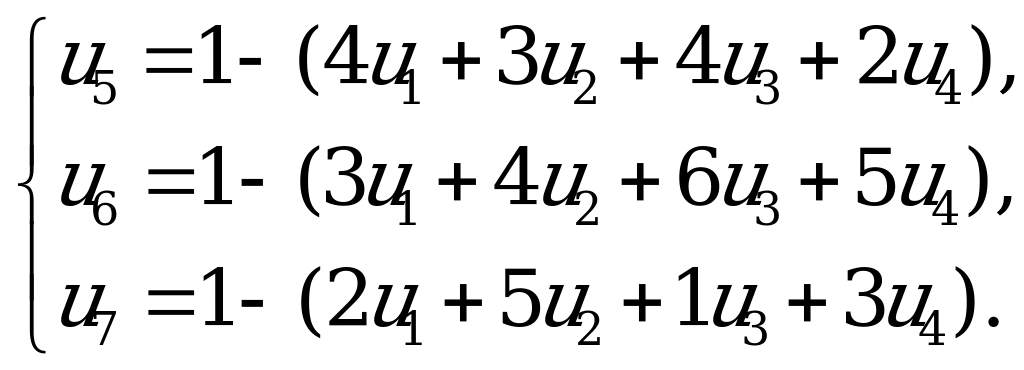
| 1 | bi | u1 | u2 | u3 | u4 |
|
| u5 | 1 | 4 | 3 | 4 | 2 | 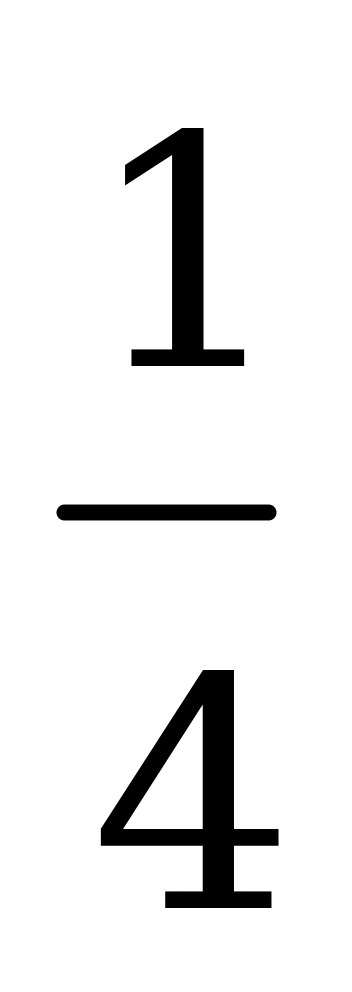
|
| u6 | 1 | 3 | 4 | 6 | 5 | 
|
| u7 | 1 | 2 | 5 | 1 | 3 | 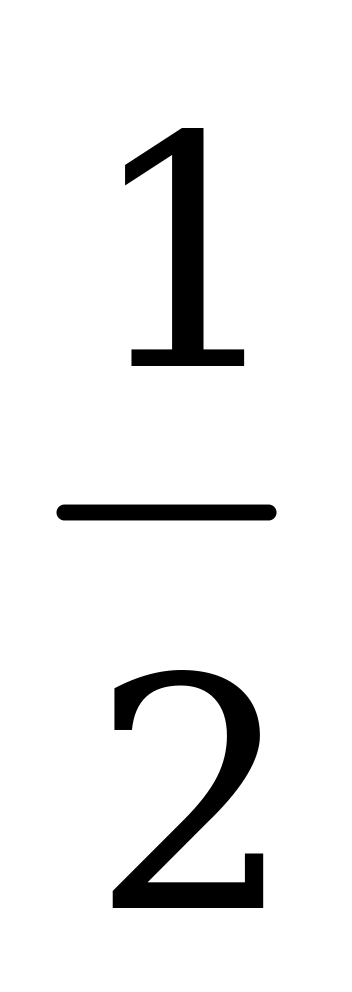
|
| 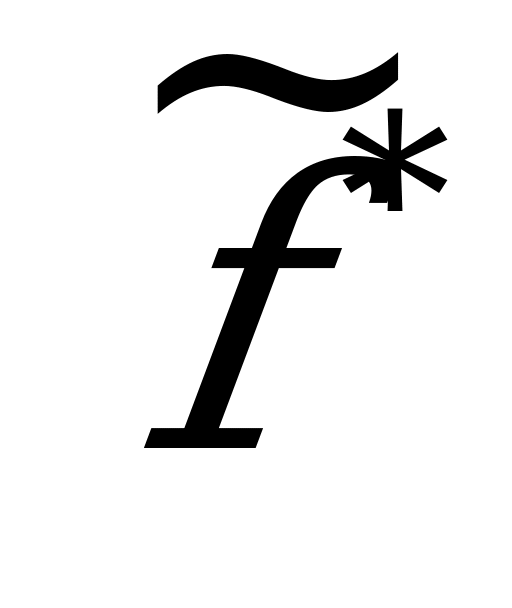
| 0 | 1 | 1 | 1 | 1 |
|
| 2 | bi | u5 | u2 | u3 | u4 |
|
| u1 | 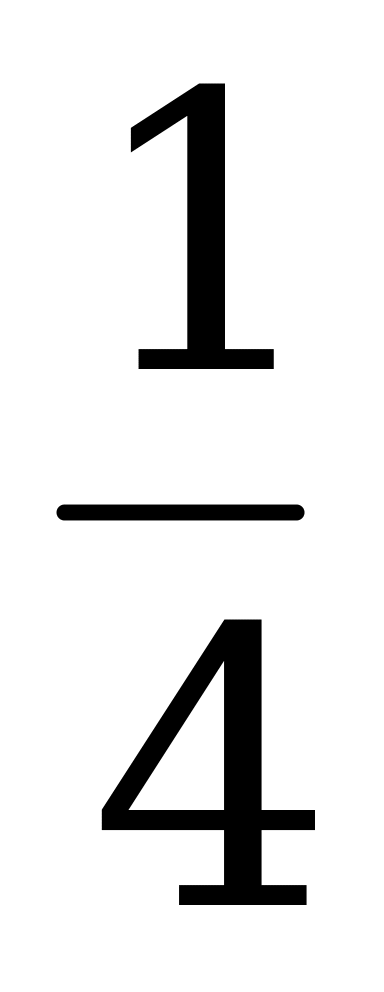
| 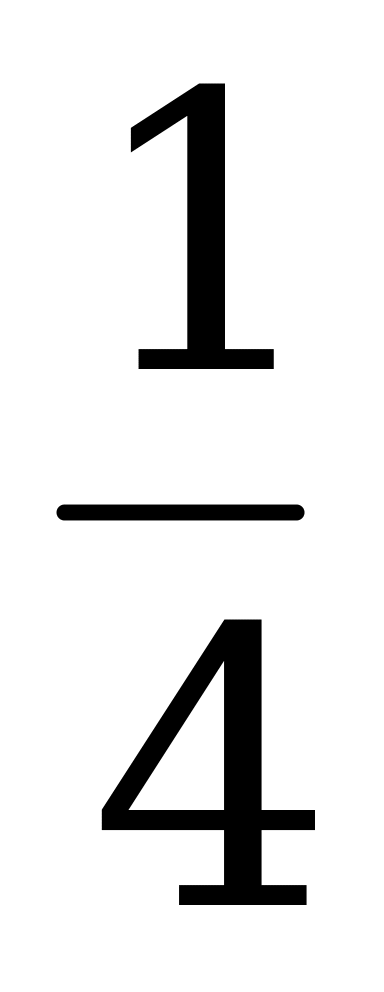
| 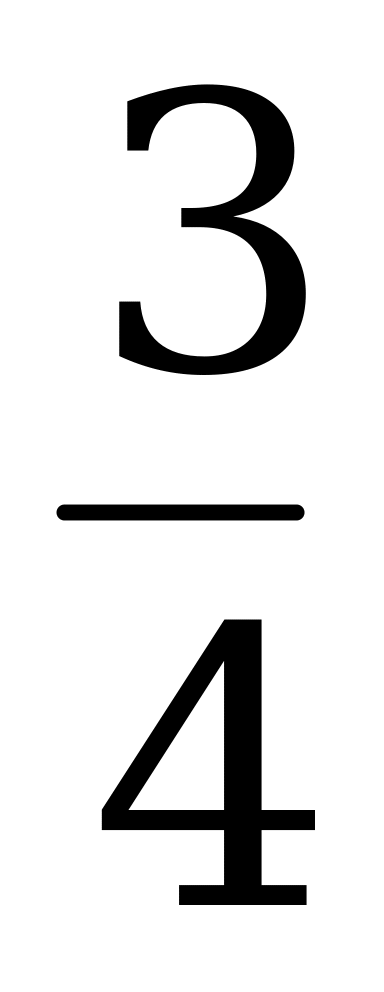
| 1 | 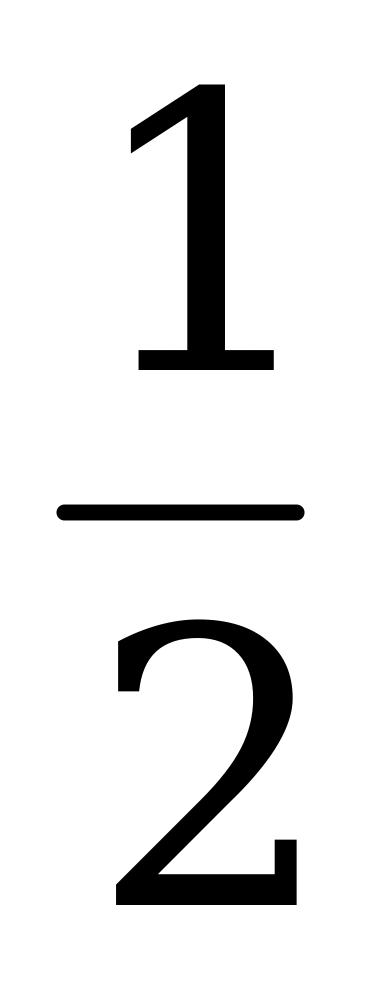
| 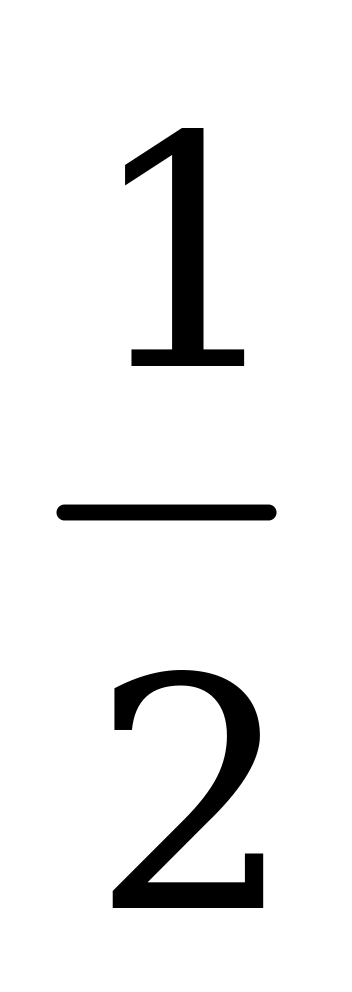
|
| u6 | 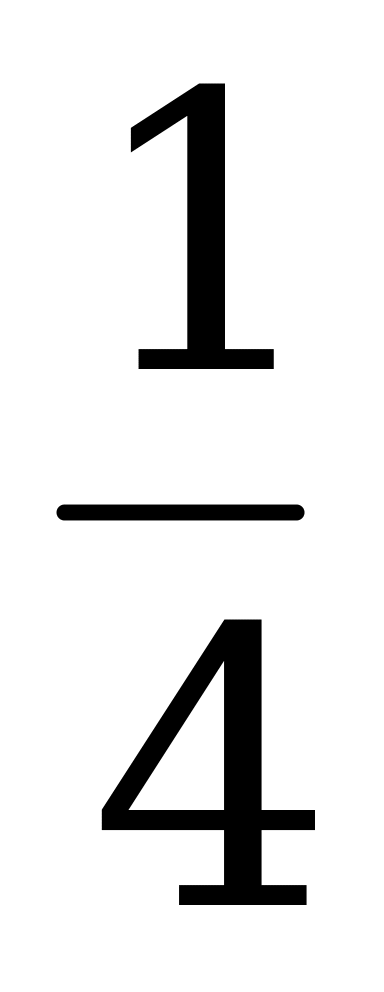
| 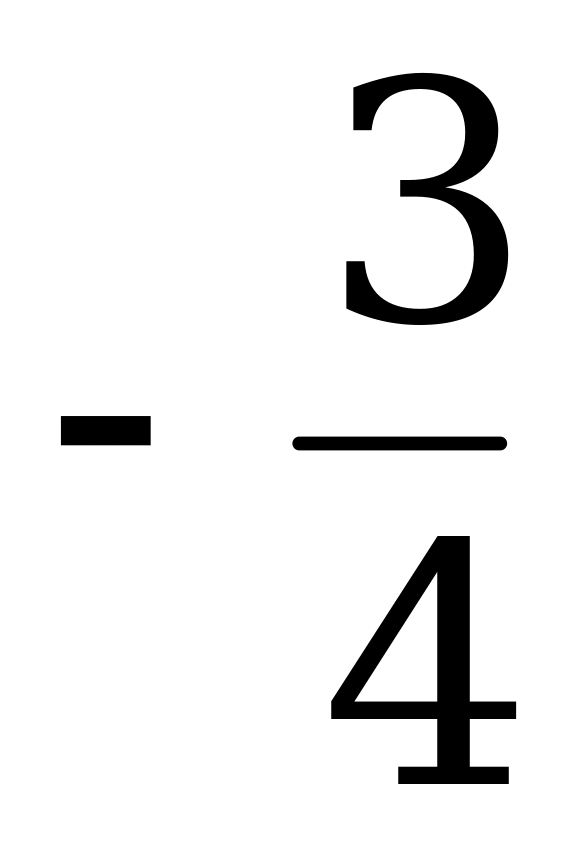
| 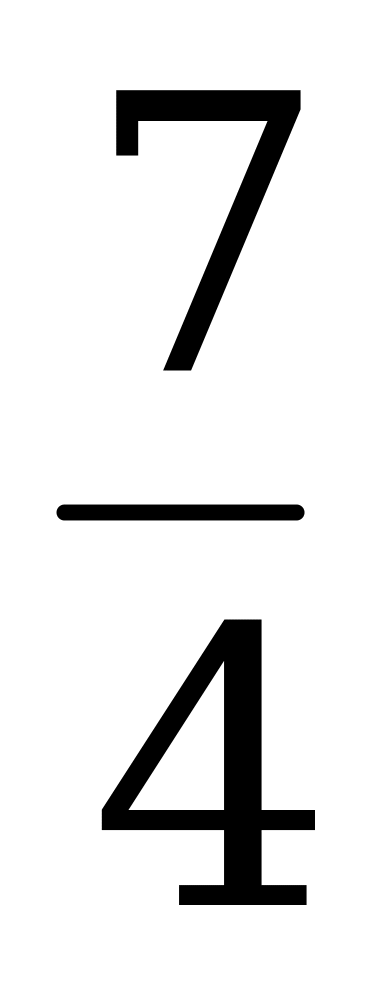
| 3 | 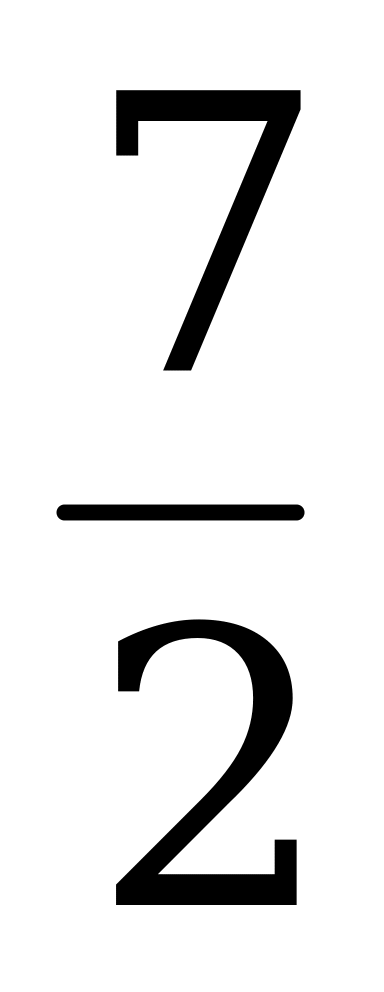
| 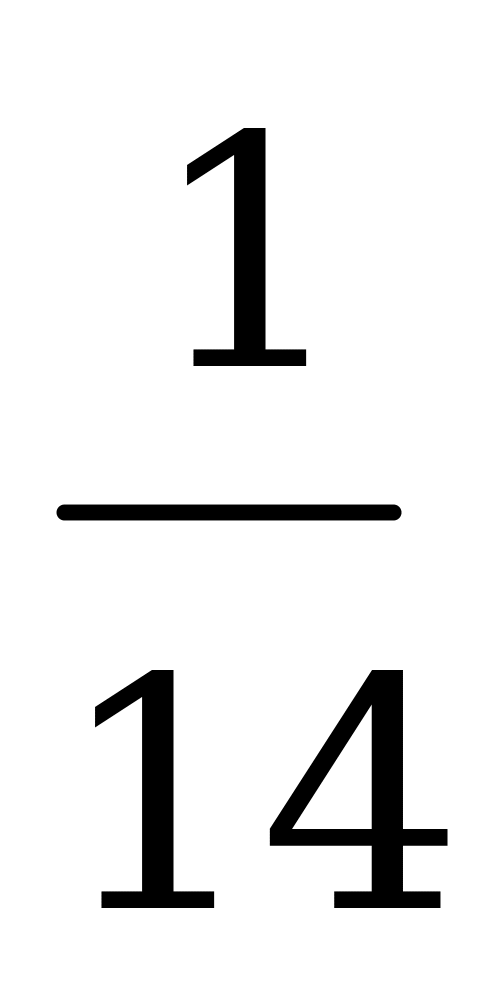
|
| u7 | 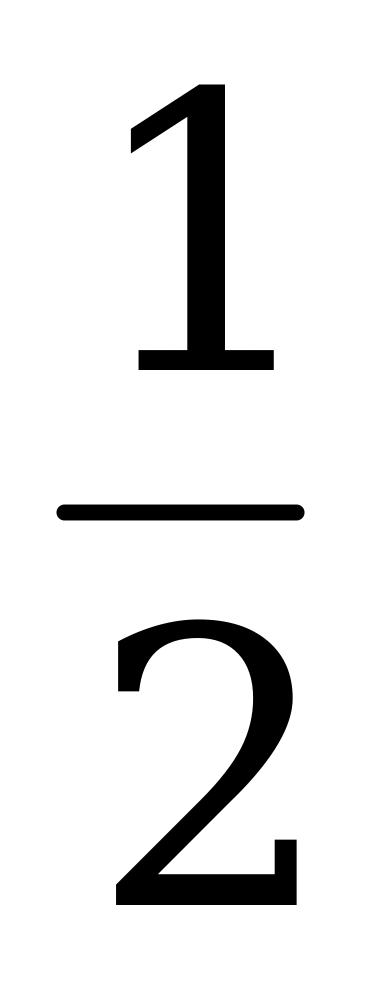
| 
| 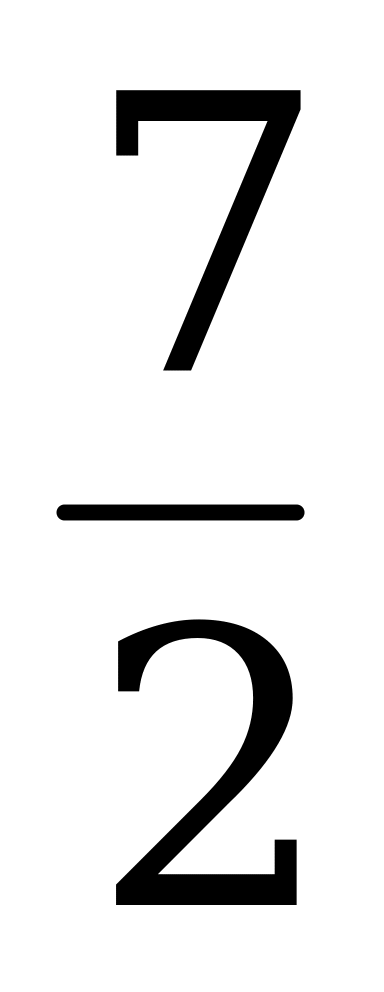
| -1 | 2 | 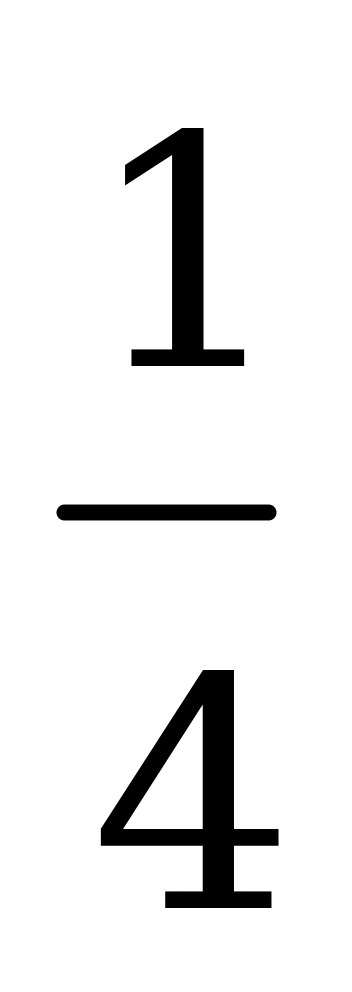
|
| 
| 
| 
| 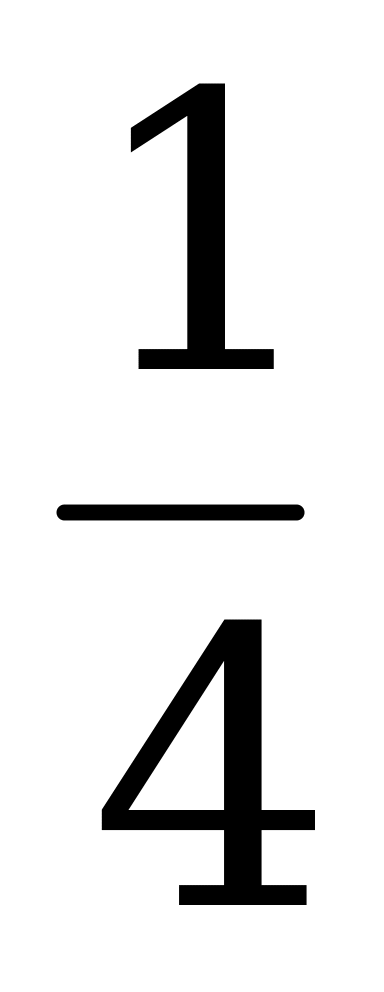
| 0 | 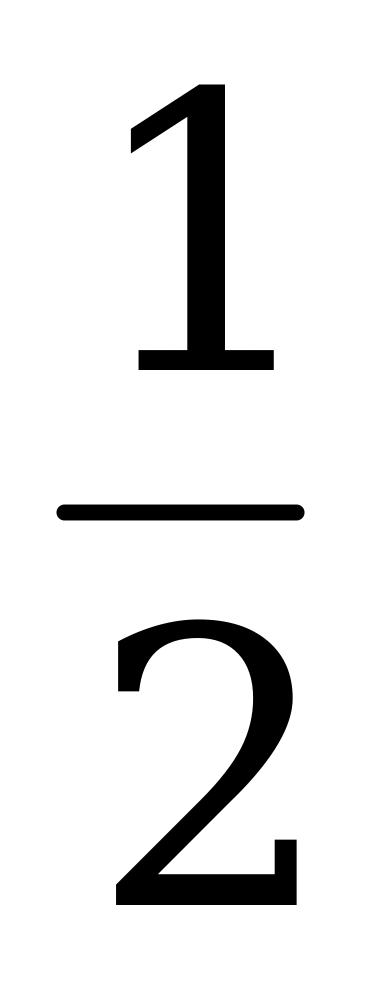
|
|
| 3 | bi | u5 | u2 | u3 | u6 |
| u1 | 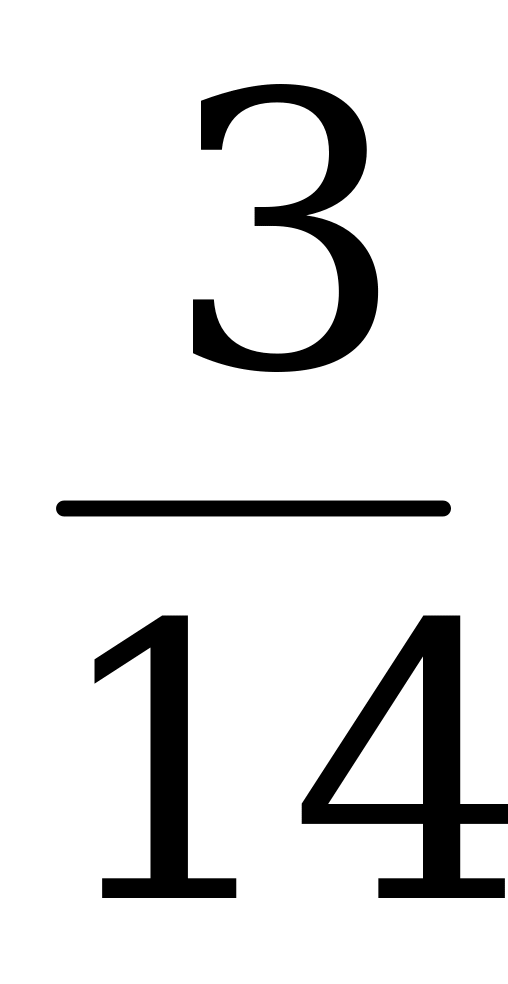
|
|
|
|
|
| u4 | 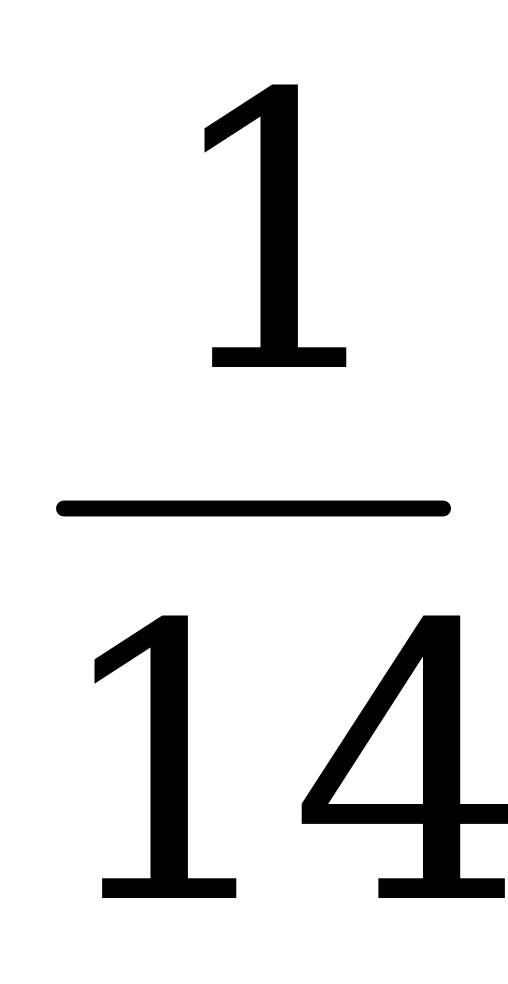
|
|
|
|
|
| u7 | 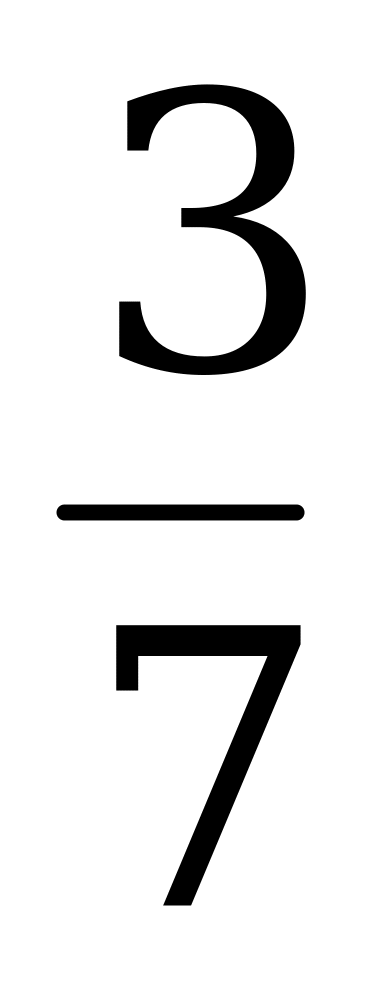
|
|
|
|
|
| 
| 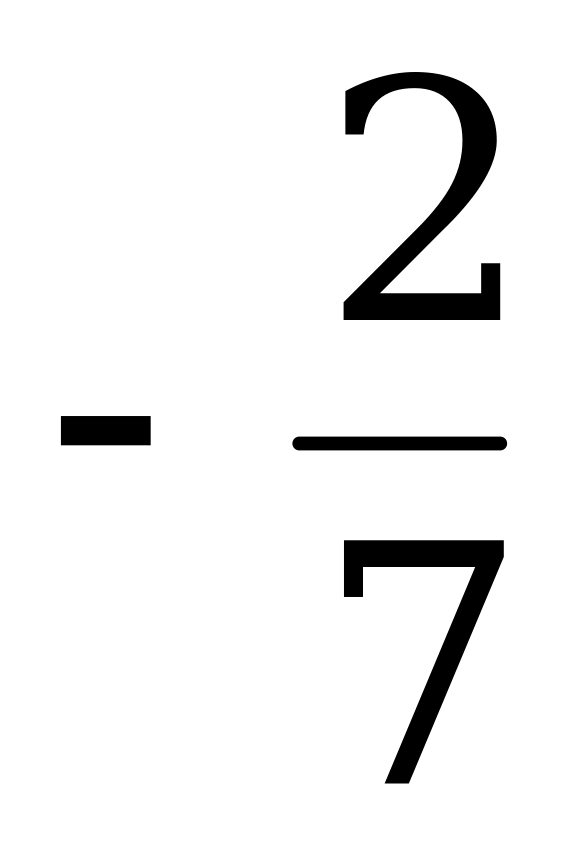
| 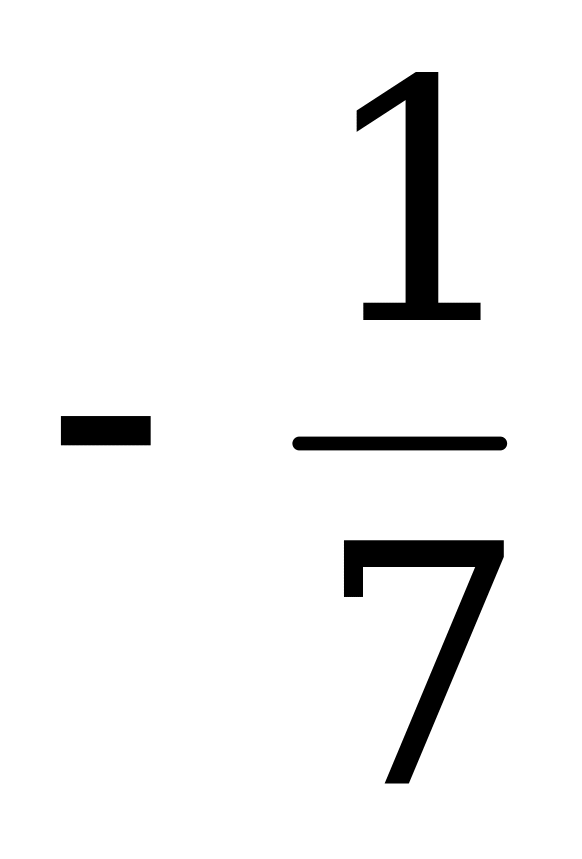
| 0 | 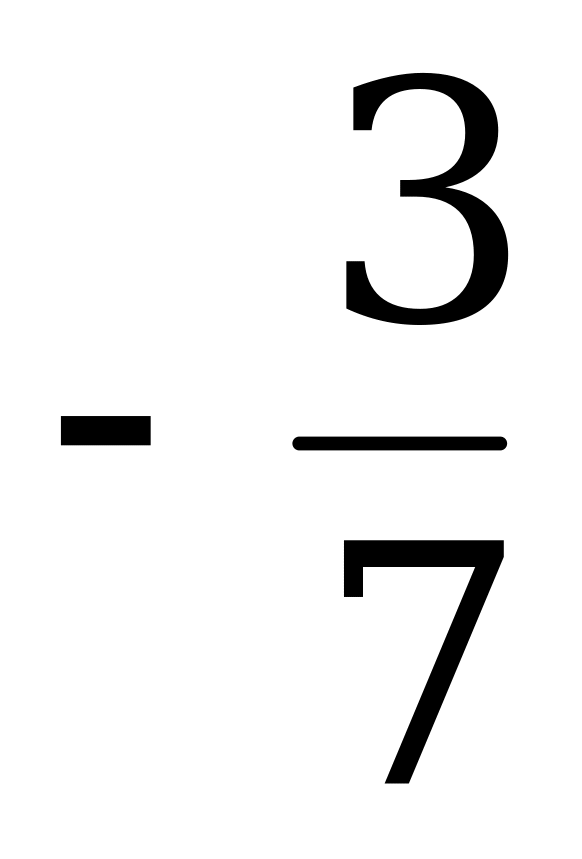
| 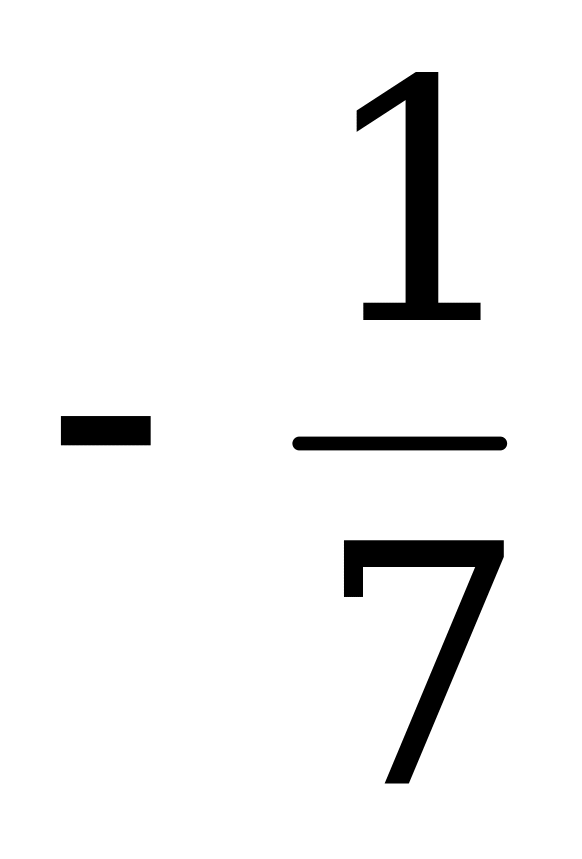
|
|
|
|
|
|
|
|
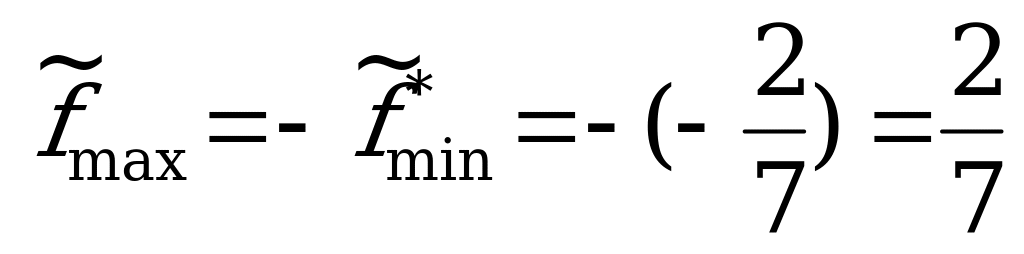
Цена игры 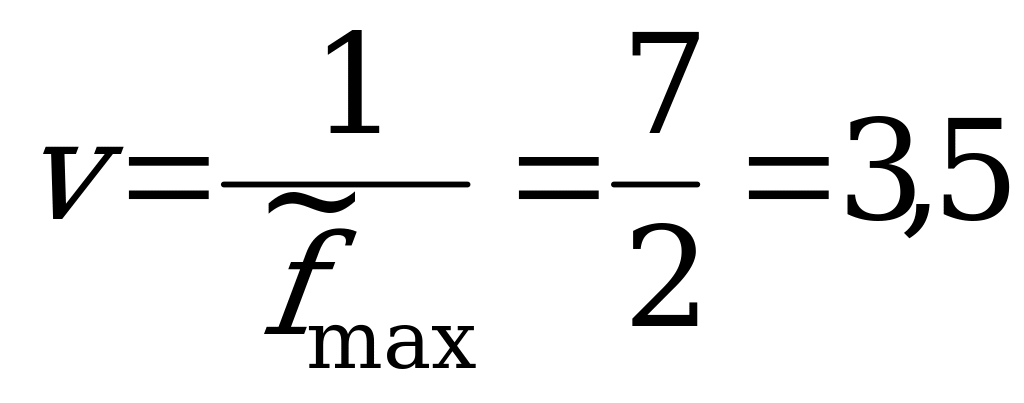 .
.
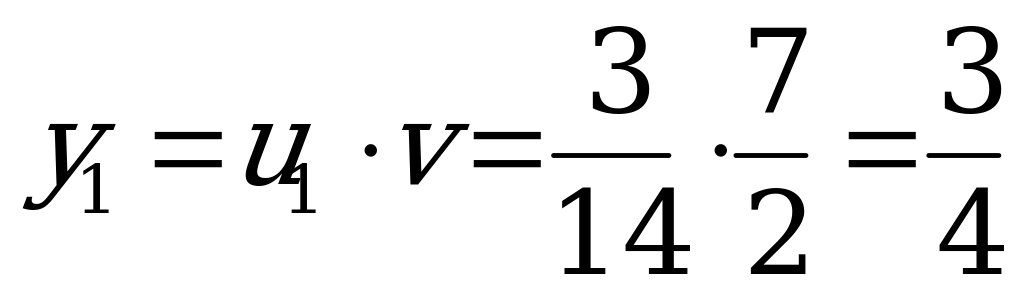 ,
,
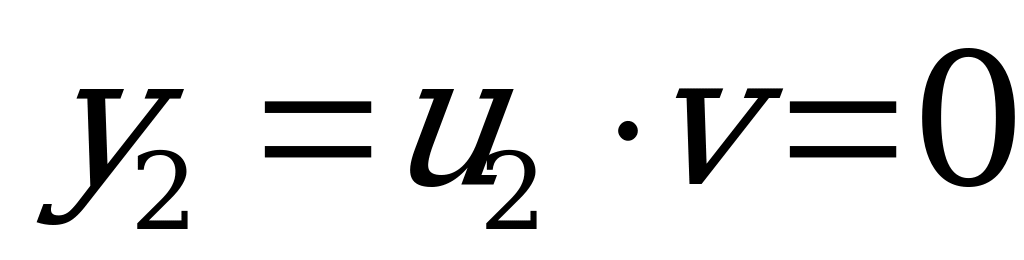 ,
,
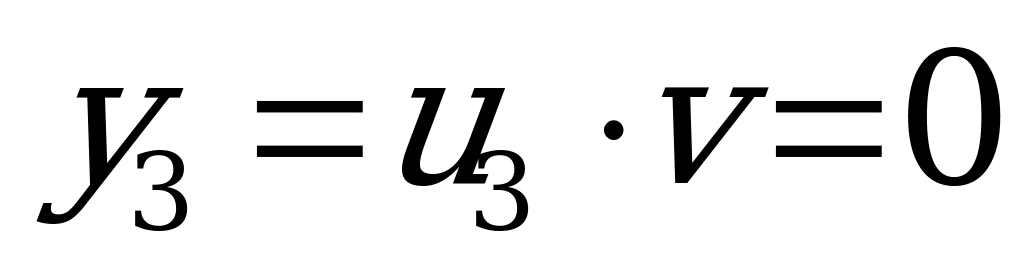 ,
,
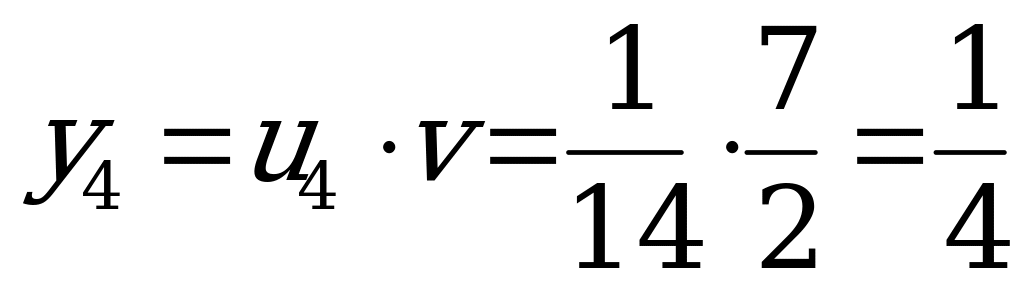 .
.
Оптимальное решение задачи для игрока  получаем, используя элементы
получаем, используя элементы  -строки последней симплексной таблицы, находящиеся в столбцах
-строки последней симплексной таблицы, находящиеся в столбцах 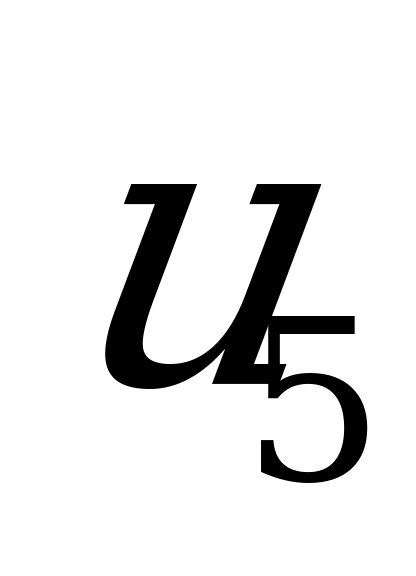 и
и  (взятые с противоположным знаком):
(взятые с противоположным знаком): 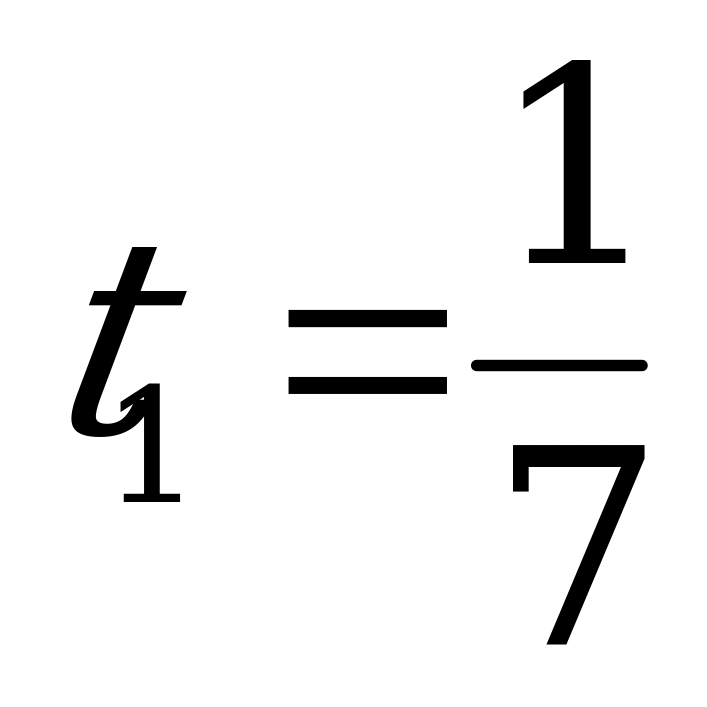 ,
, 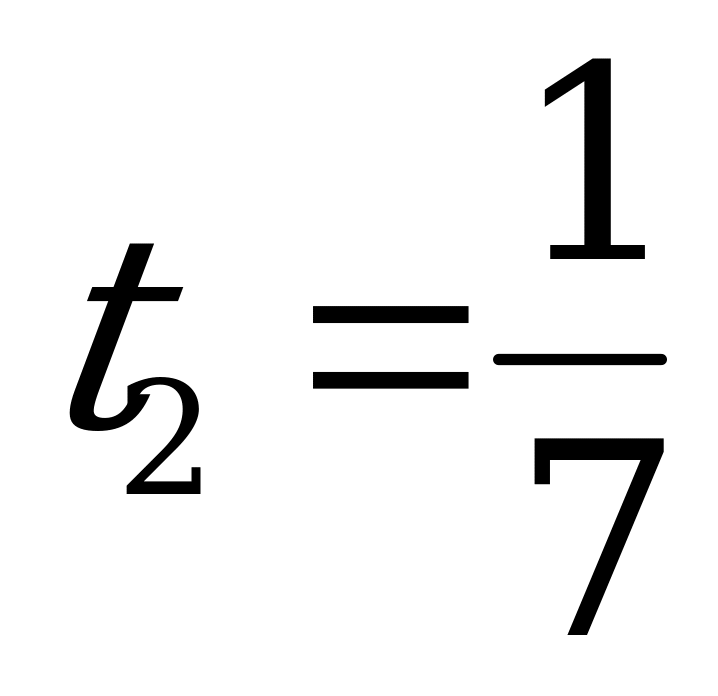 ,
, 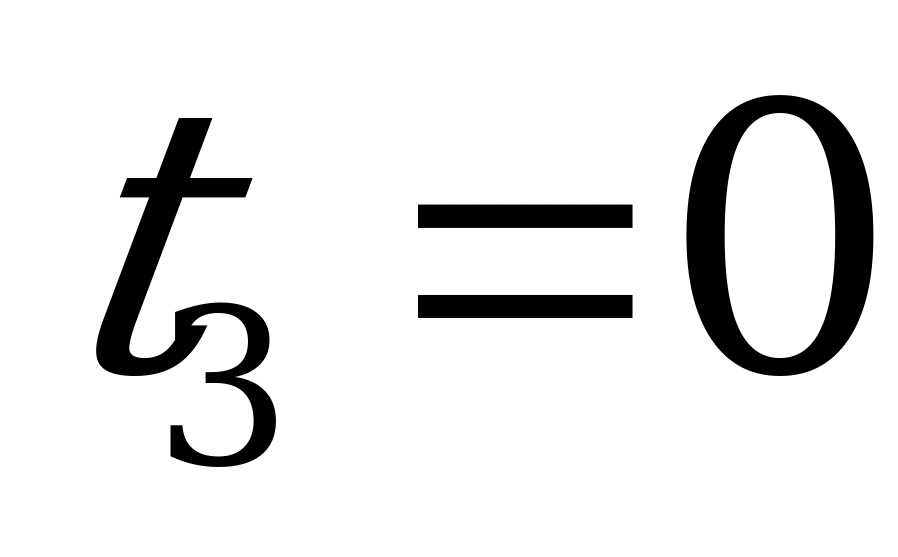 .
.
Вероятности 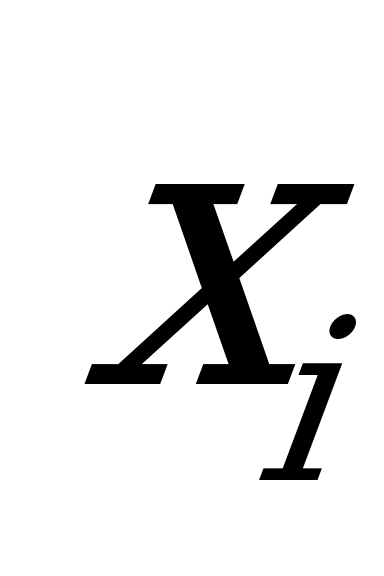 для оптимальной смешанной стратегии игрока
для оптимальной смешанной стратегии игрока  равны:
равны:
 ,
,
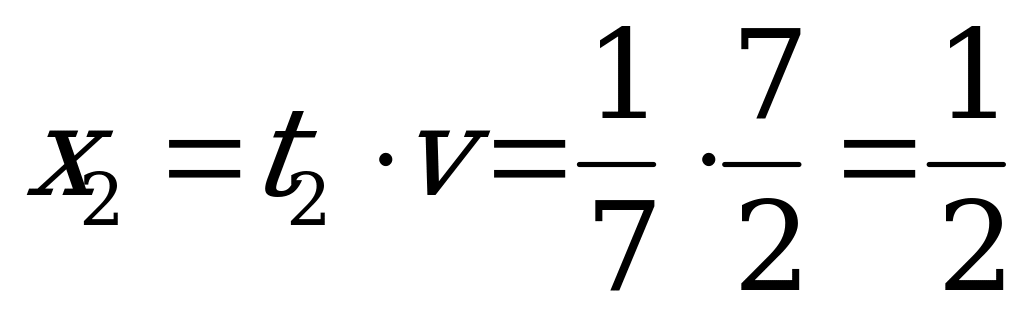 ,
,
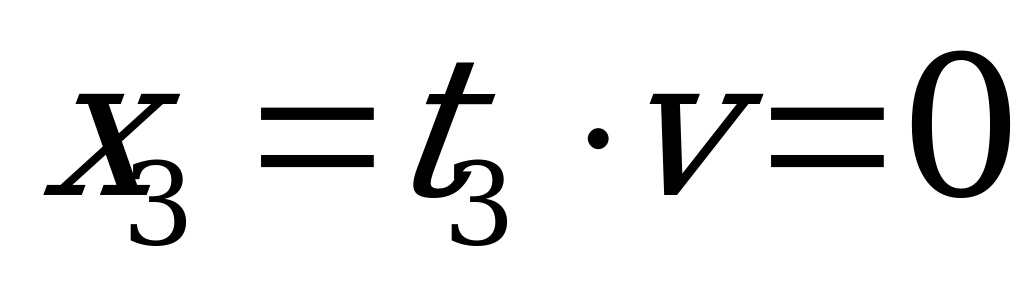 .
.
Ответ: 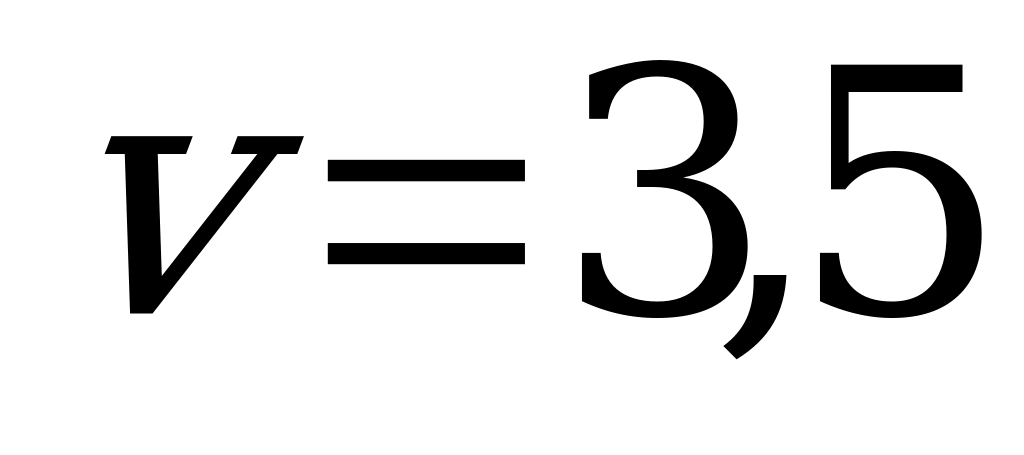 ;
; 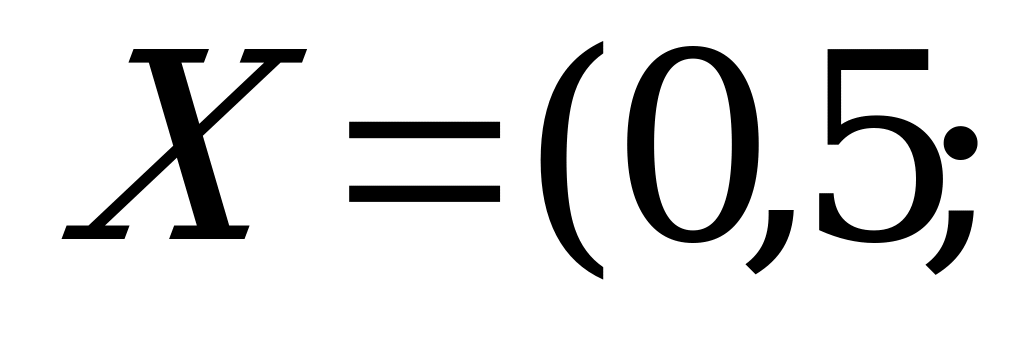
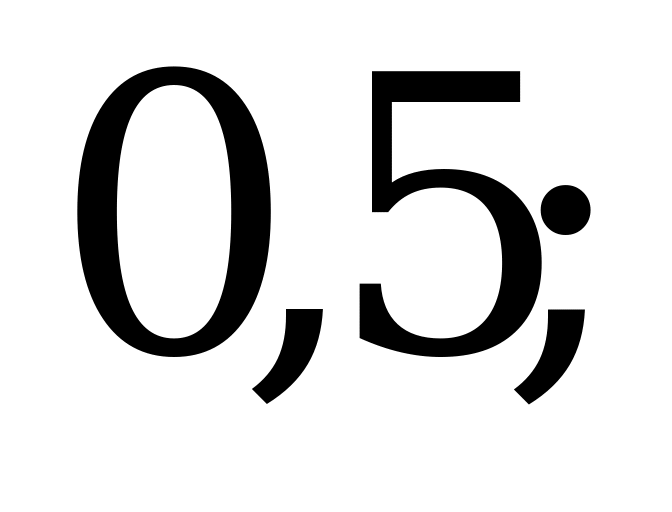
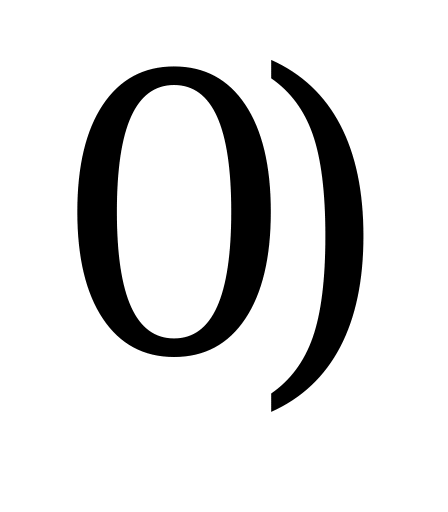 ,
, 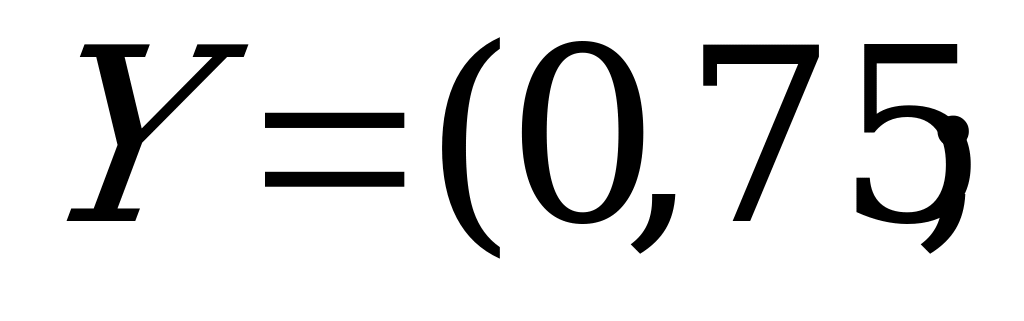
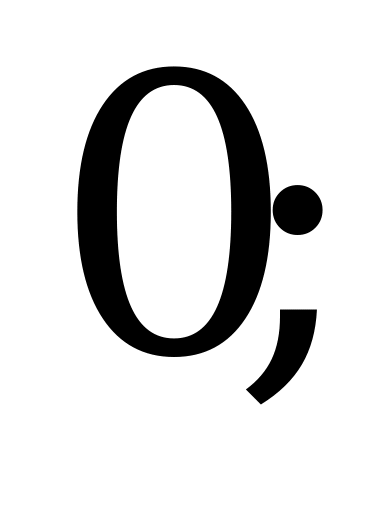
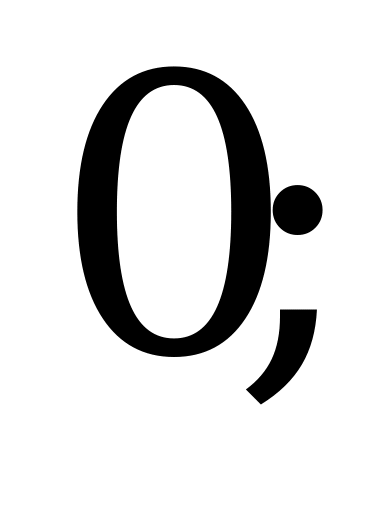
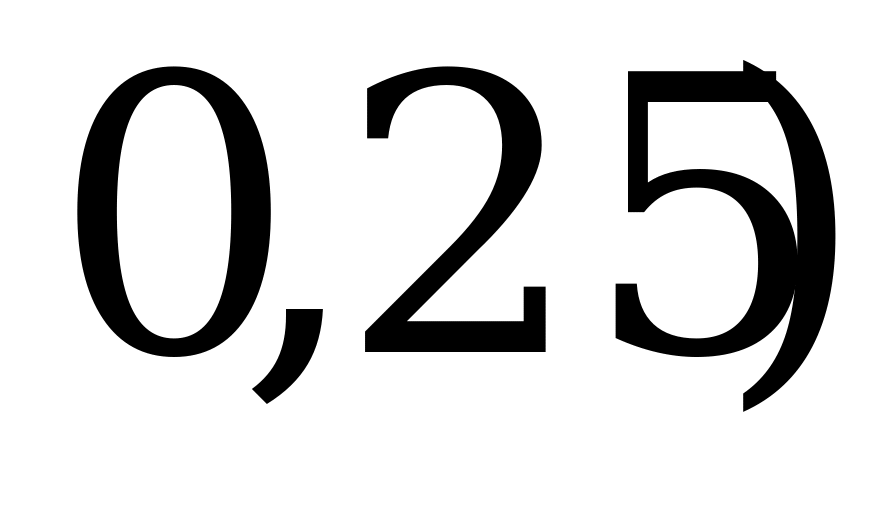 .
.
Численный метод решения игр – метод итераций
Идея метода состоит в следующем. Разыгрывается мысленный эксперимент, в котором стороны  и
и  поочерёдно применяют друг против друга свои стратегии, стремясь выиграть побольше (проиграть поменьше). Эксперимент состоит из ряда партий игры. Начинается он с того, что один из игроков (скажем,
поочерёдно применяют друг против друга свои стратегии, стремясь выиграть побольше (проиграть поменьше). Эксперимент состоит из ряда партий игры. Начинается он с того, что один из игроков (скажем,  ) выбирает произвольно одну из своих стратегий
) выбирает произвольно одну из своих стратегий  . Противник (
. Противник ( ) отвечает ему той из своих стратегий
) отвечает ему той из своих стратегий 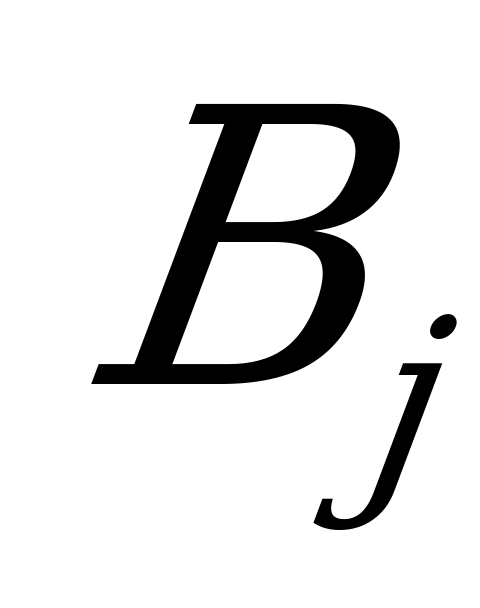 , которая хуже всего для
, которая хуже всего для  , т.е. обращает его выигрыш при стратегии
, т.е. обращает его выигрыш при стратегии  в минимум. Дальше снова очередь
в минимум. Дальше снова очередь  - он отвечает
- он отвечает  той своей стратегией
той своей стратегией 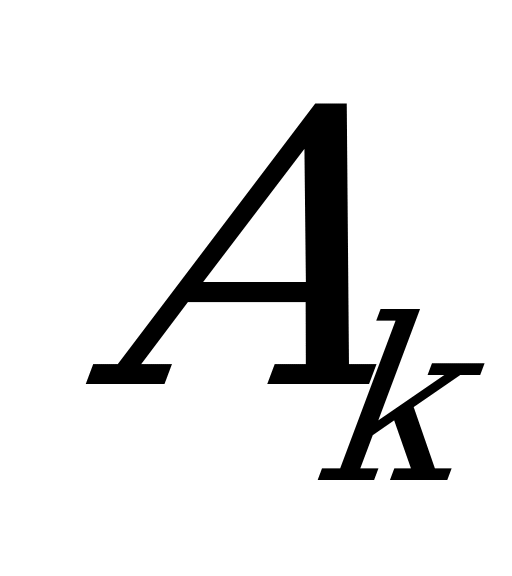 , которая даёт максимальный выигрыш при стратегии
, которая даёт максимальный выигрыш при стратегии 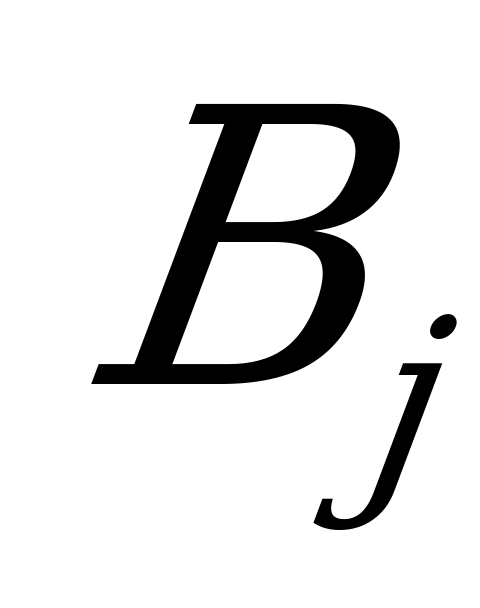 противника. Дальше – снова очередь противника. Он отвечает нам той своей стратегией, которая является наихудшей не для последней, применённой нами, стратегии
противника. Дальше – снова очередь противника. Он отвечает нам той своей стратегией, которая является наихудшей не для последней, применённой нами, стратегии 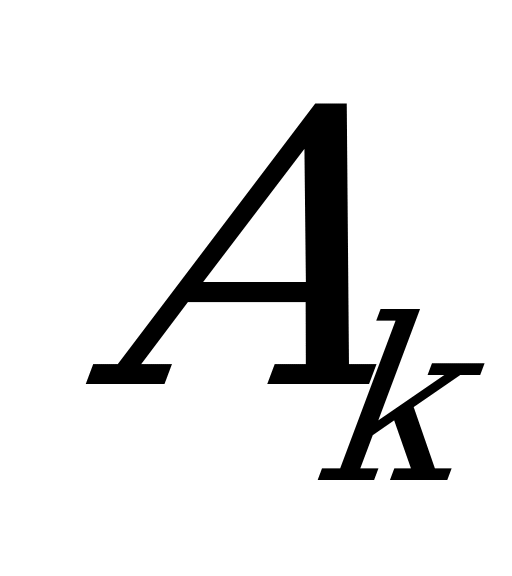 , а для смешанной стратегии, в которой до сих пор применённые стратегии
, а для смешанной стратегии, в которой до сих пор применённые стратегии  ,
, 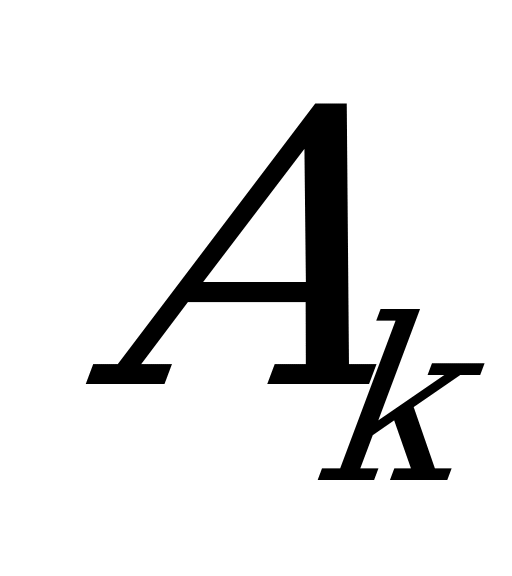 встречаются с равными вероятностями. И так далее: на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той своей стратегией, которая является оптимальной для него относительно смешанной стратегии другого, в которую все применённые до сих пор стратегии входят пропорционально частотам их применения.
встречаются с равными вероятностями. И так далее: на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той своей стратегией, которая является оптимальной для него относительно смешанной стратегии другого, в которую все применённые до сих пор стратегии входят пропорционально частотам их применения.
Вместо того чтобы вычислять средний выигрыш, можно пользоваться просто «накопленным» за предыдущие ходы выигрышем и выбирать ту стратегию, при которой этот накопленный выигрыш максимален (минимален). Доказано, что такой метод сходится: при увеличении числа партий средний выигрыш за одну партию будет стремится к цене игры, а частоты применения стратегий – к их вероятностям в оптимальных смешанных стратегиях игроков.
Пример 10. 


Продемонстрируем итерационный метод на примере игры 3×3 предыдущего параграфа:

.
Начнём с произвольно выбранной стратегии игрока  , например, со стратегии
, например, со стратегии  .
.
В таблице приведены первые 15 шагов итерационного процесса.
В первом столбце дан номер партии (пары выборов)  , во втором – номер
, во втором – номер 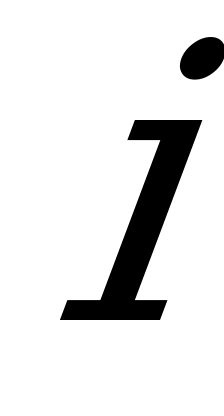 выбранной в данной партии стратегии игрока
выбранной в данной партии стратегии игрока  .
.
В последующих трёх столбцах – накопленный выигрыш за первые  партий при тех стратегиях, которые применяли игроки в предыдущих партиях и при стратегиях
партий при тех стратегиях, которые применяли игроки в предыдущих партиях и при стратегиях 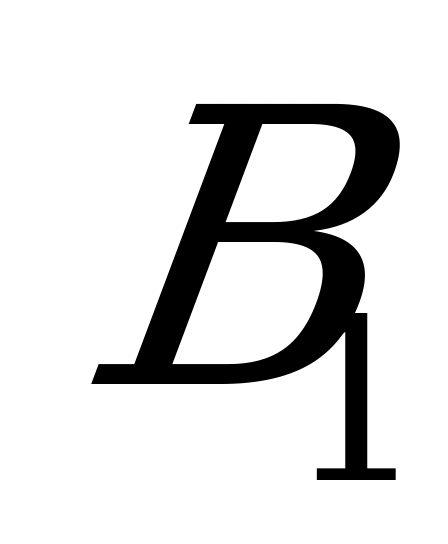 ,
, 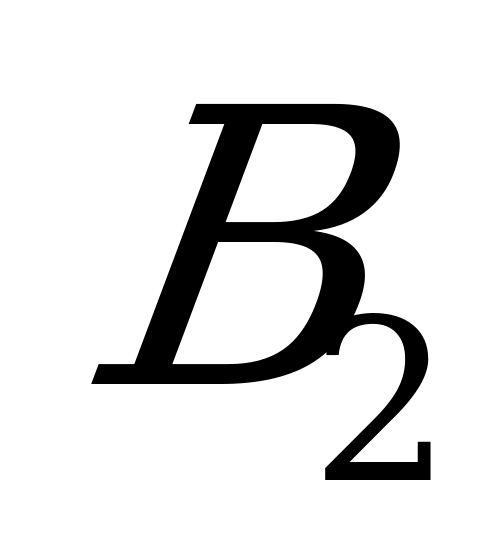 ,
, 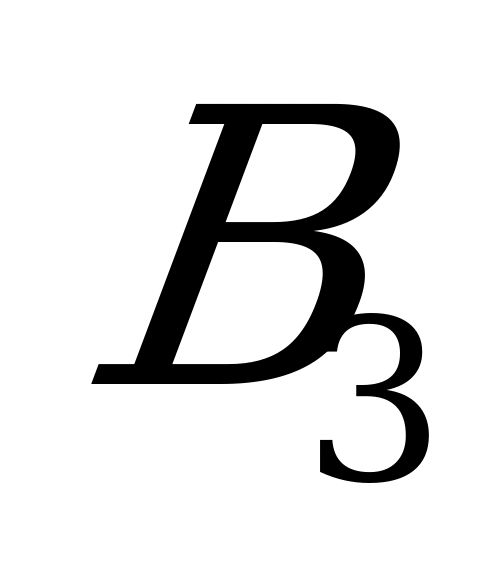 игрока
игрока  в данной партии (получается прибавлением элементов соответствующей строки к тому, что было строкой выше). Из этих накопленных выигрышей выделяется минимальный (если их несколько, выделяются все). Выделенное число определяет ответный выбор игрока
в данной партии (получается прибавлением элементов соответствующей строки к тому, что было строкой выше). Из этих накопленных выигрышей выделяется минимальный (если их несколько, выделяются все). Выделенное число определяет ответный выбор игрока  в данной партии – он выбирает ту стратегию, которая соответствует выделенному числу (если их несколько, берётся любая). Таким образом определяется номер
в данной партии – он выбирает ту стратегию, которая соответствует выделенному числу (если их несколько, берётся любая). Таким образом определяется номер  оптимальной в данной партии стратегии
оптимальной в данной партии стратегии  .
.
В последующих трёх столбцах даётся накопленный выигрыш за  партий соответственно при стратегиях
партий соответственно при стратегиях  ,
, 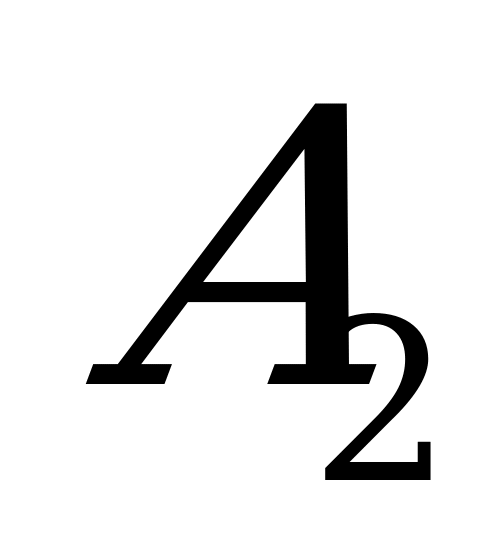 ,
,  игрока
игрока  (получается прибавлением элементов столбца
(получается прибавлением элементов столбца 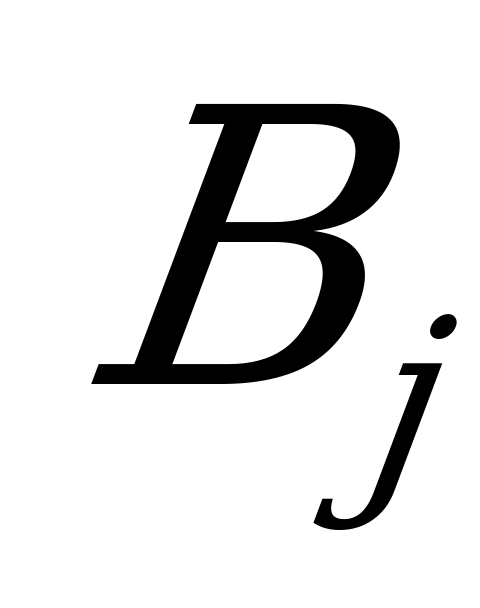 к тому, что было строкой выше). Из этих значений выделяется максимальное; оно определяет выбор стратегии игрока
к тому, что было строкой выше). Из этих значений выделяется максимальное; оно определяет выбор стратегии игрока  в следующей партии (строкой ниже).
в следующей партии (строкой ниже).
В последних трёх столбцах таблицы даны:
 - нижняя оценка цены игры, равная минимальному накопленному выигрышу, делённому на число партий
- нижняя оценка цены игры, равная минимальному накопленному выигрышу, делённому на число партий  ;
;
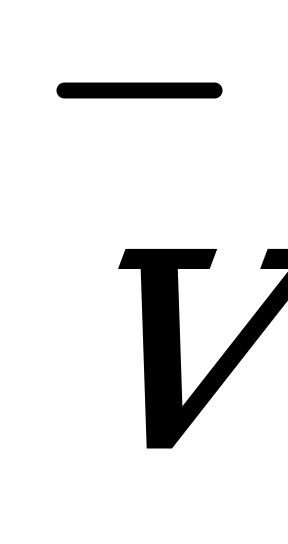 - верхняя оценка цены игры, равная максимальному накопленному выигрышу, делённому на число партий
- верхняя оценка цены игры, равная максимальному накопленному выигрышу, делённому на число партий  ;
;
 - среднее арифметическое между
- среднее арифметическое между  и
и 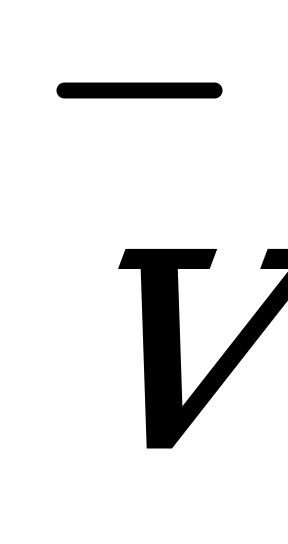 (оно служит приближённой оценкой цены игры).
(оно служит приближённой оценкой цены игры).
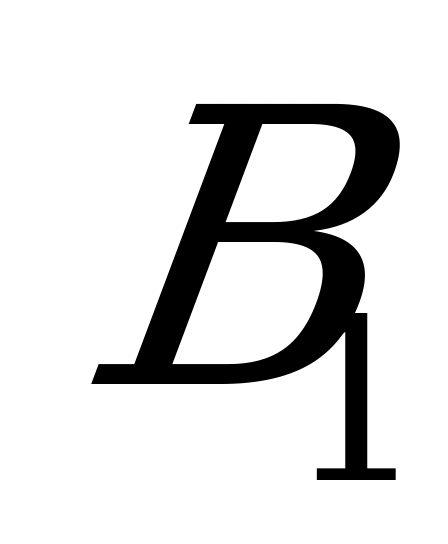
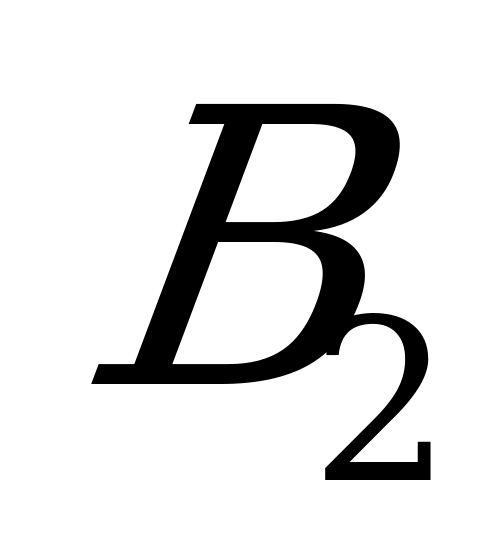
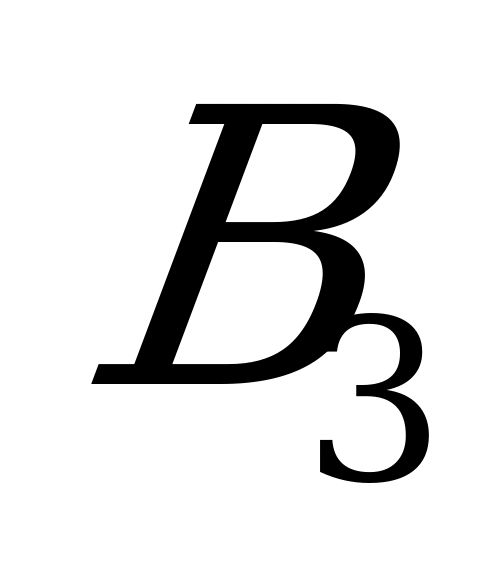



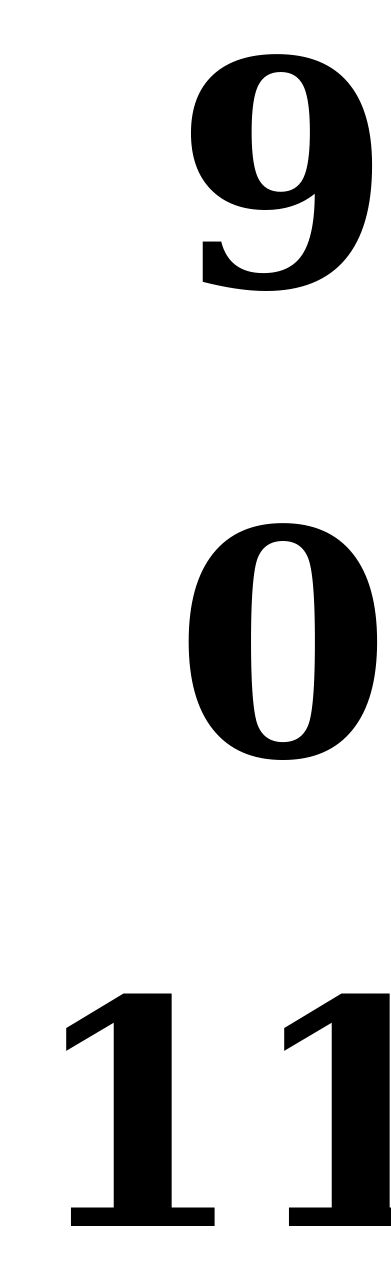
 .
.
| Номер партии | Номер выбранной в данной партии стра-тегии игрока А | Накопленный проигрыш игрока В за k партий | Номер оптимальной в данной партии стратегии игрока В | Накопленный выигрыш игрока А за k партий | Минимум по столбцам В1, В2, В3, делённый на k | Максимум по столбцам А1, А2, А3, делённый на k | Среднее арифмети-ческое предыдущих двух столбцов |
| 
| 
| 
|  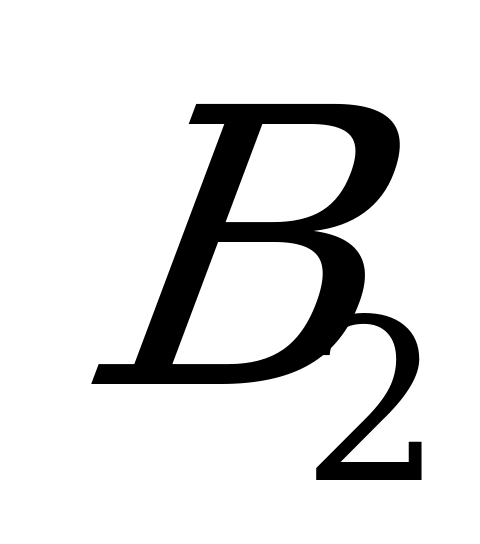
| 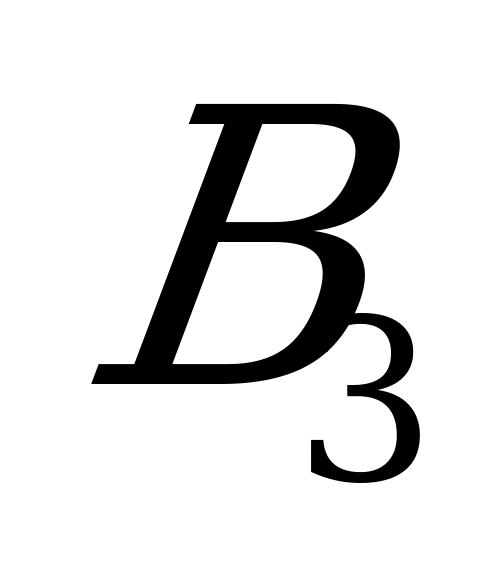
| 
| 
|  
| 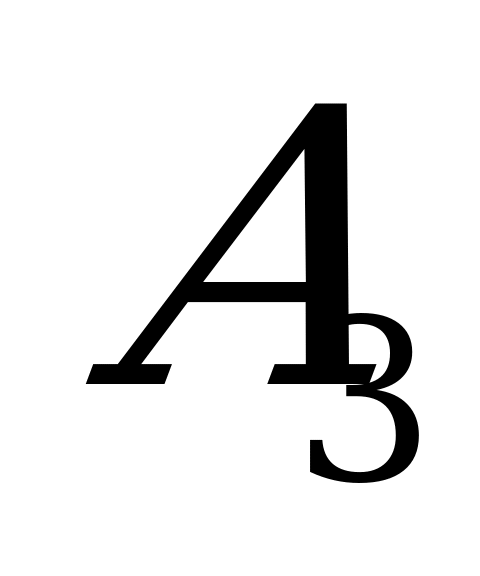
| 
| 
| 
|
| 1 | 3 | 9 | 0 | 11 | 2 | 2 | 9 | 0 | 0 | 9 | 4,5 |
| 2 |  2 2
| (2) 11 | (9) 9 | (0) 11 |  2 2
| (2) 4 | (9) 18 | (0) 0 | 4,5 | 9 | 6,75 |
| 3 | 2 | (2) 13 | (9) 18 | (0) 11 | 3 | (9) 13 | (0) 18 | (11) 11 | 3,67 | 6 | 4,84 |
| 4 | 2 | (2) 15 | (9) 27 | (0) 11 | 3 | (9) 22 | (0) 18 | (11) 22 | 2,75 | 5,5 | 4,13 |
| ( б е р ё т с я л ю б а я ) |
| 5 | 1 | (7) 22 | (2) 29 | (9) 20 | 3 | (9) 31 | (0) 18 | (11) 33 | 4 | 6,6 | 5,3 |
| 6 | 3 | (9) 31 | (0) 29 | (11) 31 | 2 | (2) 33 | (9) 27 | (0) 33 | 4,84 | 5,5 | 5,17 |
| 7 | 1 | 38 | 31 | 40 | 2 | 35 | 36 | 33 | 4,43 | 5,14 | 4,79 |
| 8 | 2 | 40 | 40 | 40 | 2 | 37 | 45 | 33 | 5 | 5,61 | 5,3 |
| 9 | 2 | 42 | 49 | 40 | 3 | 46 | 45 | 44 | 4,45 | 5,11 | 4,78 |
| 10 | 1 | 49 | 51 | 49 | 1 | 53 | 47 | 53 | 4,9 | 5,3 | 5,1 |
| 11 | 3 | 58 | 51 | 60 | 2 | 55 | 56 | 53 | 4,64 | 5,09 | 4,87 |
| 12 | 2 | 60 | 60 | 60 | 2 | 57 | 65 | 53 | 5 | 5,41 | 5,2 |
| 13 | 2 | 62 | 69 | 60 | 3 | 66 | 65 | 64 | 4,61 | 5,07 | 4,84 |
| 14 | 1 | 69 | 71 | 69 | 1 | 73 | 67 | 73 | 4,93 | 5,21 | 5,07 |
| 15 | 3 | 78 | 71 | 80 | 2 | 75 | 76 | 73 | 4,74 | 5,06 | 4,9 |
Как видно, величина  незначительно колеблется около цены игры
незначительно колеблется около цены игры 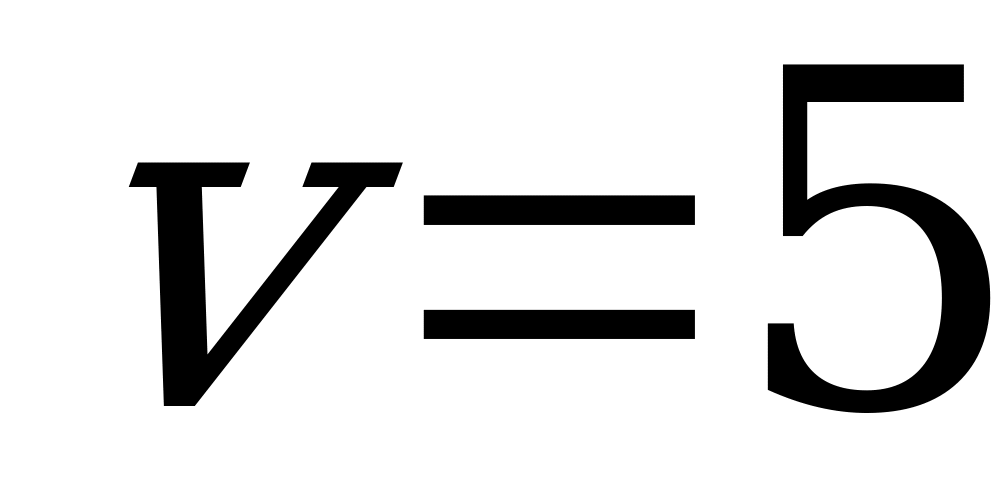 (цена исходной игры была 0, но мы прибавили к элементам матрицы по 5).
(цена исходной игры была 0, но мы прибавили к элементам матрицы по 5).
Подсчитаем по таблице частоты 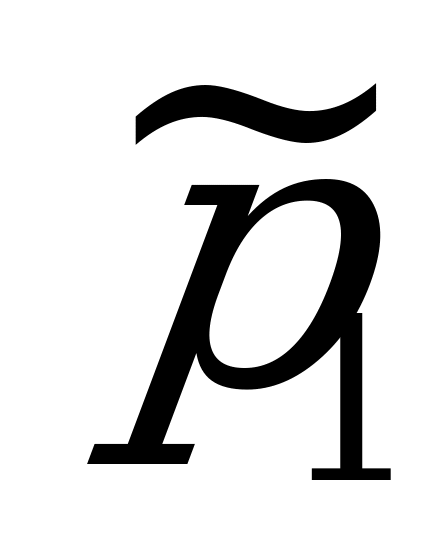 ,
, 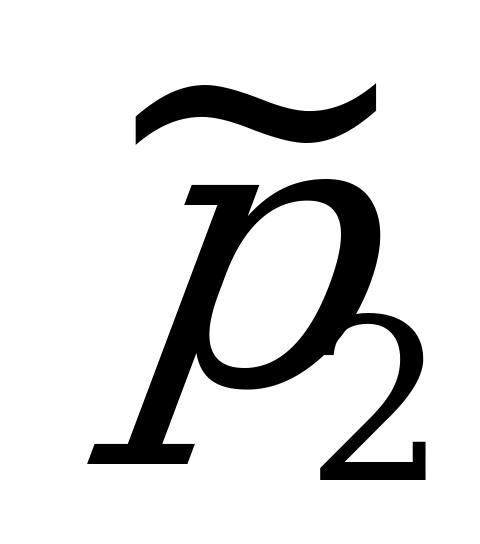 ,
, 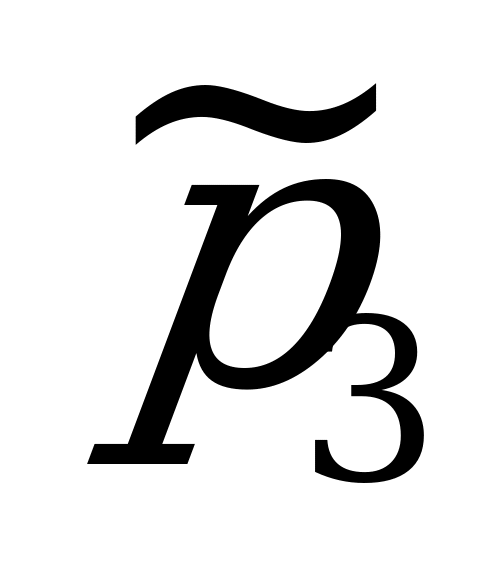 ,
, 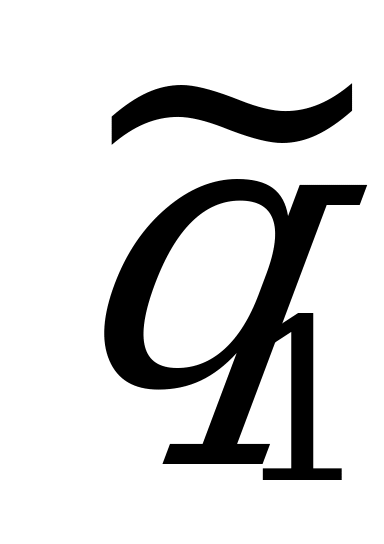 ,
, 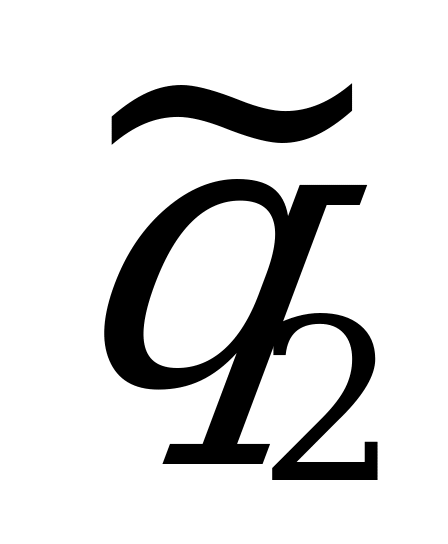 ,
, 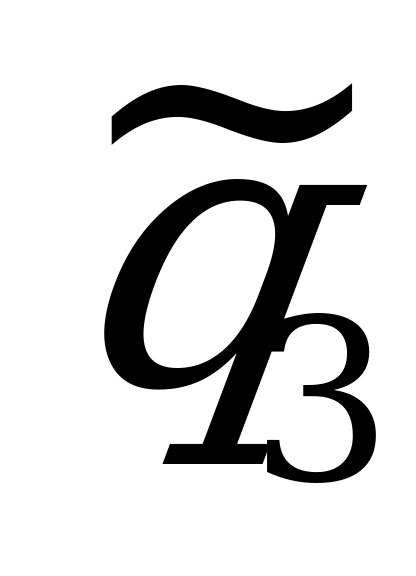 стратегий игроков. Получим:
стратегий игроков. Получим:
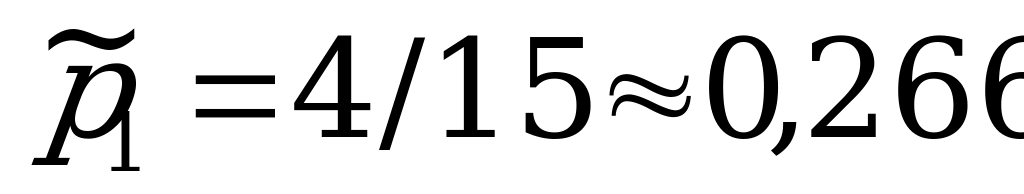 ;
; 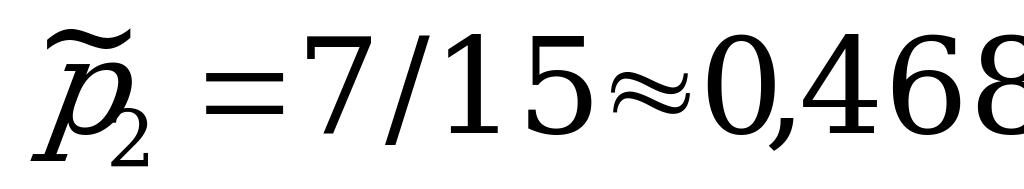 ;
; 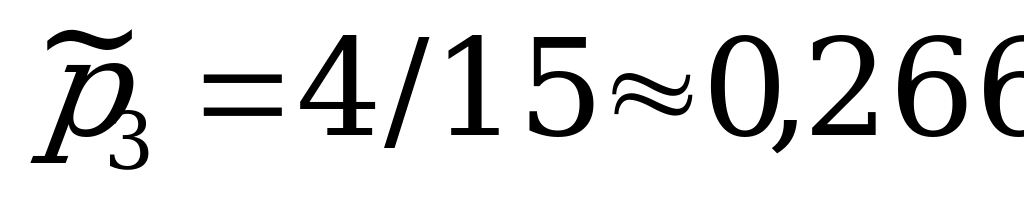 ;
;
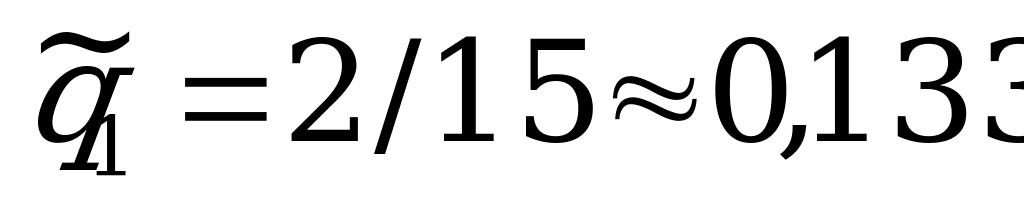 ;
; 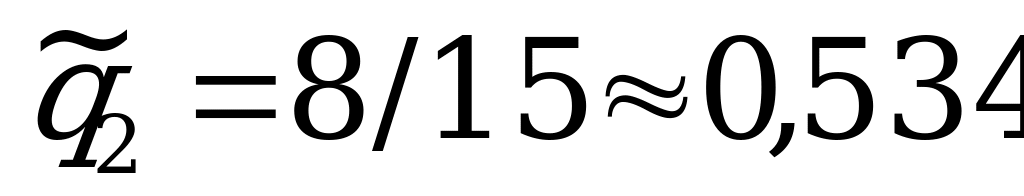 ;
; 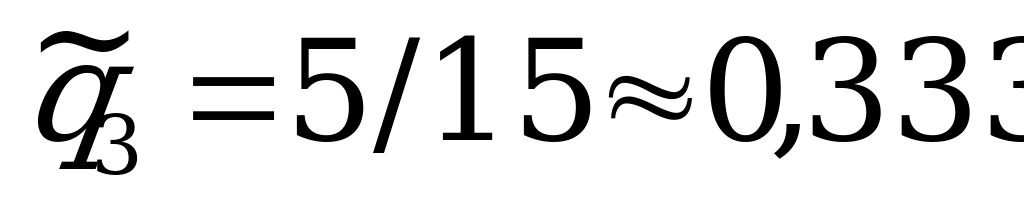 ,
,
что не так уж сильно отличается от вероятностей 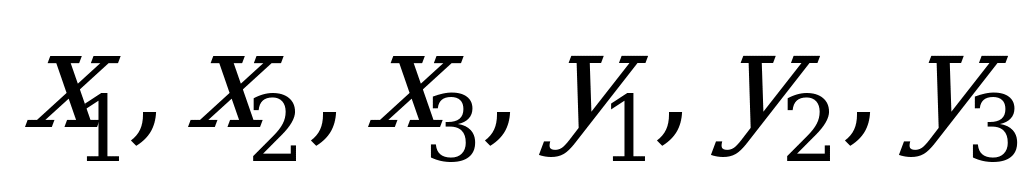 , равных, как мы определили раньше, для первой, второй и третьей стратегий соответственно
, равных, как мы определили раньше, для первой, второй и третьей стратегий соответственно
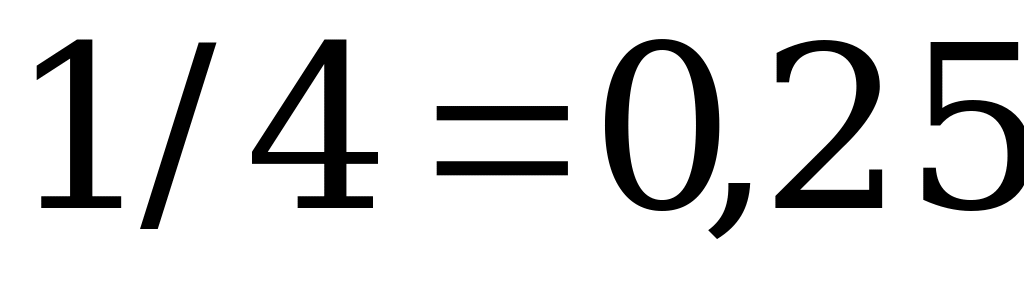 ;
; 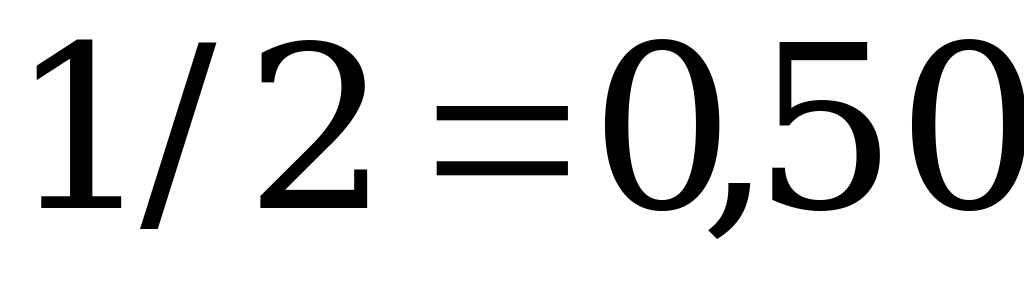 ;
; 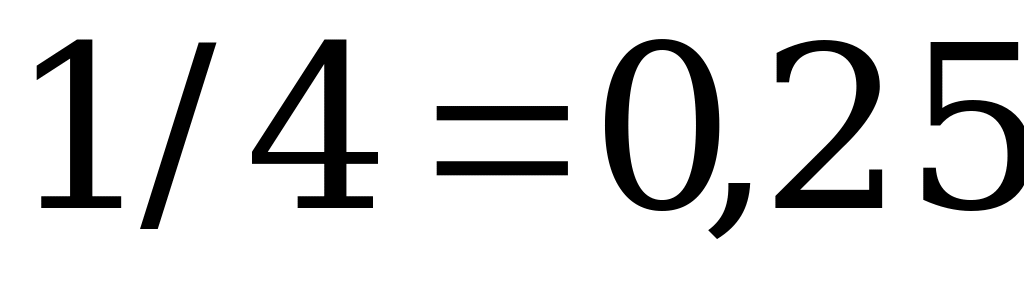 .
.
О чень важным преимуществом итерационного метода решения игр является то, что его трудоёмкость сравнительно медленно возрастает с увеличением размерности игры
чень важным преимуществом итерационного метода решения игр является то, что его трудоёмкость сравнительно медленно возрастает с увеличением размерности игры 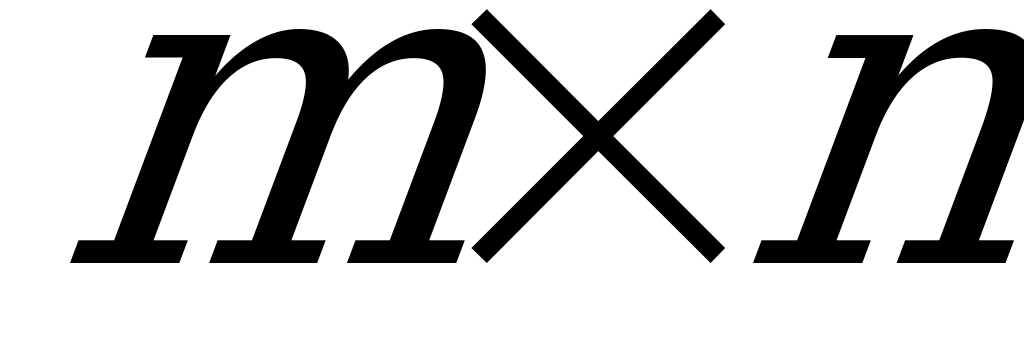 , тогда как трудоёмкость метода линейного программирования растёт при увеличении размерности задачи гораздо быстрее.
, тогда как трудоёмкость метода линейного программирования растёт при увеличении размерности задачи гораздо быстрее.
Заключение
-
В теории игр рассматриваются задачи, в которых имеется несколько лиц, принимающих решения.
-
Они действуют сознательно (разумно).
-
Предполагается, что вся информация об игре (множества стратегий, функции выигрышей) известна всем игрокам, неизвестно, какую стратегию из возможных выберет противник в данной партии игры.
-
При поиске оптимальной стратегии руководствуются принципом «максимина» («минимакса»)1, т.е. рассматривается наихудшая ситуация для данного игрока.
-
Оптимальная стратегия в игре двух лиц с нулевой суммой обеспечивает одному игроку выигрыш, не меньший некоторого числа (цены игры  ), а другому – проигрыш, не больший
), а другому – проигрыш, не больший  .
.
-
«Смешанные» стратегии состоят в том, что игрок применяет не одну какую-то стратегию («чистую»), а несколько, перемежая их случайным образом.
Смешанные стратегии могут применяться, когда речь идёт о многократно повторяемой игре (ситуации). Но бывают ситуации, когда решение надо принять одно-единственное (выбрать план строительства системы оборонительных сооружений). В этом случае не следует делать выбор случайным образом, хоть это и вытекает из принципов теории игр, а следует руководствоваться и какими-то другими соображениями.
В 2005 году Нобелевская премия по экономике присуждена Томасу Шеллингу и Роберту Ауманну за вклад в лучшее понимание конфликта и сотрудничества при помощи теории игр. Оба лауреата посвятили не один десяток лет теории игр и получили премию за анализ социальных проблем при помощи этой теории. При этом Ауманн занимался проблемой сотрудничества и конфликтов с точки зрения математики, а Шеллинг – с точки зрения экономики.
2005 году Нобелевская премия по экономике присуждена Томасу Шеллингу и Роберту Ауманну за вклад в лучшее понимание конфликта и сотрудничества при помощи теории игр. Оба лауреата посвятили не один десяток лет теории игр и получили премию за анализ социальных проблем при помощи этой теории. При этом Ауманн занимался проблемой сотрудничества и конфликтов с точки зрения математики, а Шеллинг – с точки зрения экономики.
Томас Шеллинг – профессор университета Мэриленда (США). Его книга «Стратегия конфликта», вышедшая в 1960 году и положившая начало исследованиям стратегического поведения и торгов, была признана одной из сотни наиболее влиятельных книг послевоенного времени. Шеллинг – основоположник теории сдерживания, положенной в основу ядерной стратегии США. Шеллинг показал, что игрок может усилить свою позицию при помощи сужения числа доступных вариантов, причем способность ответить ударом на удар может быть более ценной, чем способность отразить атаку. Характерно, что гарантированный ответный удар с точки зрения его теории менее эффективен, чем негарантированный. Работы Шеллинга помогли избежать войны и разрешить многие конфликты.
Роберт Ауманн – профессор университета в Иерусалиме (Израиль). Он сумел продемонстрировать, что социальные взаимодействия могут быть проанализированы при помощи формальной теории некоалиционных игр, первым провёл полный формальный анализ так называемых бесконечно повторяющихся игр.
Теория повторяющихся игр позволяет глубже понять предпосылки к кооперации - в частности, почему совместная работа затрудняется при большом числе участников. Кроме того, данная теория раскрывает природу таких экономических конфликтов, как ценовые и торговые войны.
Теория ядерных игр
Нобелевская премия по экономике присуждена Роберту Ауманну и Томасу Шеллингу "за вклад в лучшее понимание конфликта и сотрудничества при помощи теории игр". Премия достается нескольким лауреатам уже в шестой раз подряд. За аналогичные исследования 11 лет назад премию по экономике получили Джон Нэш (ставший прототипом главного героя в фильме "Игры разума"), Рейнхард Зелтен и Джон Харсаньи.
Центральной концепцией вопроса тогда, в 1994 году, стало равновесие по Нэшу - комбинация стратегий игроков, при которой стратегия каждого оптимальна для игры против других. Харсаньи, в свою очередь, удалось показать, что эта ключевая концепция может быть распространена на игры с недостаточной информацией (то есть такие, где игроки не знают предпочтений друг друга). Зелтен продемонстрировал, что та же концепция работает для динамических игр и игр, где игроки могут совершать ошибки с бесконечно малой вероятностью.
Тем не менее, без применения инструментария теории игр к проблемам общества эти выводы принесли бы мало пользы. Нынешние лауреаты получили премию как раз за анализ социальных проблем при помощи теории игр. При этом Ауманн занимался проблемой сотрудничества и конфликтов с точки зрения математики, а Шеллинг - с точки зрения экономики. Так, Шеллингу удалось показать, что многие общественные взаимодействия можно рассмотреть как некоалиционные игры, которые включают в себя как общие, так и противоположные интересы участников. Ауманн, в свою очередь, сумел продемонстрировать, что социальные взаимодействия могут быть проанализированы при помощи формальной теории некоалиционных игр.
Исследователи показали, что сотрудничество проще поддерживать в долговременных отношениях, а не в краткосрочных. Более того, анализ кратковременных игр часто не оставляет игрокам свободы. В частности, Роберт Ауманн первым провел полный формальный анализ так называемых бесконечно повторяющихся игр, что позволило выявить, какие выгоды дают долговременные отношения.
Теория повторяющихся игр позволяет глубже понять предпосылки к кооперации - в частности, почему совместная работа затрудняется при большом числе участников. Кроме того, данная теория раскрывает природу таких экономических конфликтов, как ценовые и торговые войны.
Шеллинг, в свою очередь, внес крупный вклад в теорию торга - в одной из своих первых работ он рассмотрел торг как двустороннее взаимодействие и исследовал тактику игроков, позволяющую им склонить чашу весов в свою сторону.
Познакомимся чуть ближе с самими исследователями.
Роберт Ауманн
Роберту Ауманну 75 лет, он профессор Еврейского университета в Иерусалиме (Израиль). Докторскую степень он получил в Массачусетском технологическом институте. Ауманн - крупный специалист в неовальрасовом анализе. В 1964 году Роберт Ауманн доказал эквивалентность множества решений Эджуорта и равновесия Вальраса при условии континуума (несчетного бесконечного множества) агентов. До недавнего времени Роберт Ауманн возглавлял Общество теории игр, а в начале 90-х был президентом Израильского союза математиков. Кроме того, он является ответственным редактором Журнала Европейского математического общества. Ауманн плотно сотрудничал с Соединенными Штатами, в частности, консультировал Агентство США по контролю за вооружениями и разоружению.
Он занимается теорией игр и ее приложениями около сорока лет. Среди его известных лекций есть даже "Теория игр в Талмуде".
Томас Шеллинг
Томас Шеллинг - профессор университета Мэриленда (США). Докторскую степень Шеллинг получил в Гарварде. Он родился в 1921 году и является одним из самых пожилых лауреатов премии по экономике. В 1991 году он стал президентом Американской экономической ассоциацией и получил звание почетного члена этой организации. Кроме того, он получил награду Национальной академии наук США за "Исследование поведения для предотвращения ядерной войны".
Его книга "Стратегия конфликта", вышедшая в 1960 году и положившая начало исследованиям стратегического поведения и торгов, была признана одной из сотни наиболее влиятельных книг послевоенного времени. Шеллинг - основоположник теории сдерживания, положенной в основу ядерной стратегии США.
Кроме того, он опубликовал работы по военной стратегии, политике охраны окружающей среды, изменению климата, распространению ядерных вооружений и контролю за ними, терроризму, организованной преступности, помощи зарубежным странам и международной торговли, конфликтам и теории торга.
Шеллинг показал, что игрок может усилить свою позицию при помощи сужения числа доступных вариантов, причем способность ответить ударом на удар может быть более ценной, чем способность отразить атаку. Характерно, что гарантированный ответный удар с точки зрения его теории менее эффективен, чем негарантированный. Работы Шеллинга помогли избежать войны и разрешить многие конфликты.
Заключение
Любопытно, что большая часть работ Шеллинга вполне доступна пониманию неспециалистов, а для работ Ауманна характерны обширные не технические обсуждения полученных им математических результатов. Тем интересней будет ознакомиться с нобелевскими лекциями, которые лауреаты прочтут 8 декабря в главной аудитории Стокгольмского университета.
Кроме того, надо признать, что нынешняя премия по экономике оказалась фактически второй премией мира - такой, какой она должна быть. Ведь лауреаты, используя теорию игр, фактически спасли человечество от ядерной войны. Более того, есть определенный намек на эту взаимосвязь - ведь нынешнюю премию мира получили МАГАТЭ и его глава. Можно сказать, что, если премия мира стала авансом за спокойное будущее в то самое время, когда не самые мирные державы ведут несанкционированные ядерные исследования, то нынешняя премия по экономике - плата за относительно спокойное прошлое, в котором не было большой войны, а были лишь две иракских, вьетнамская, корейская и сотни локальных конфликтов. Их сегодняшние лауреаты предотвратить не смогли.Впрочем, стоит надеяться, что если политики снова потерпят неудачу, мир установят именно ученые. Возможно, это будут экономисты.
1 «Максимин» - максимум из минимальных значений (выигрышей), «минимакс» - минимум из максимальных значений (проигрышей).







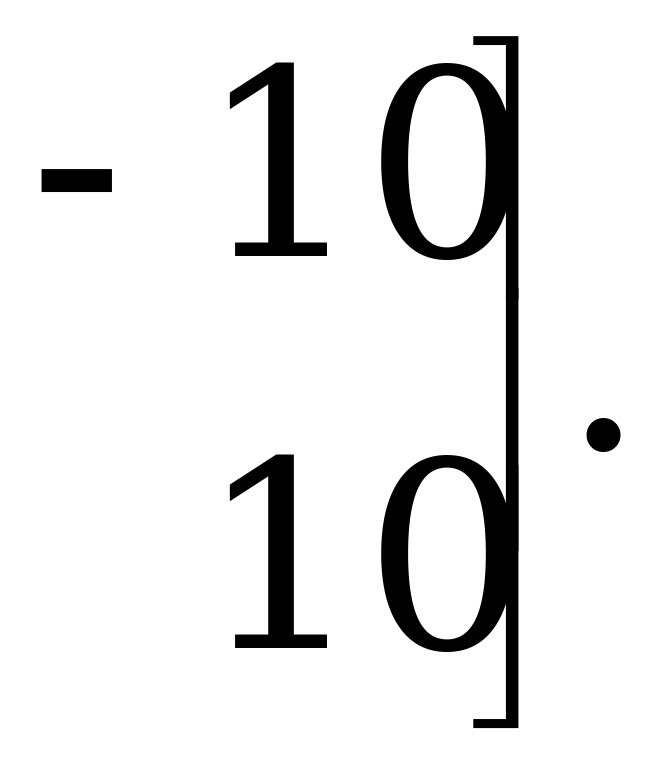
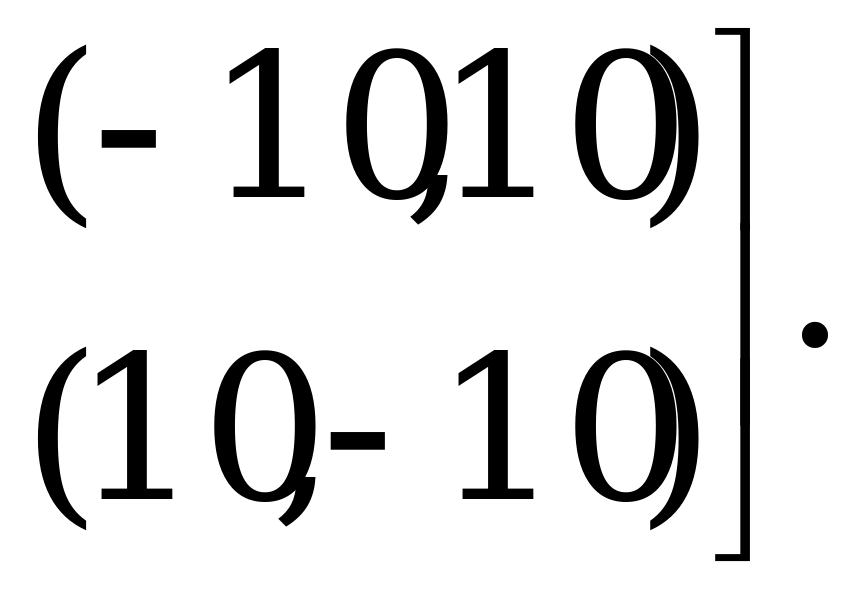
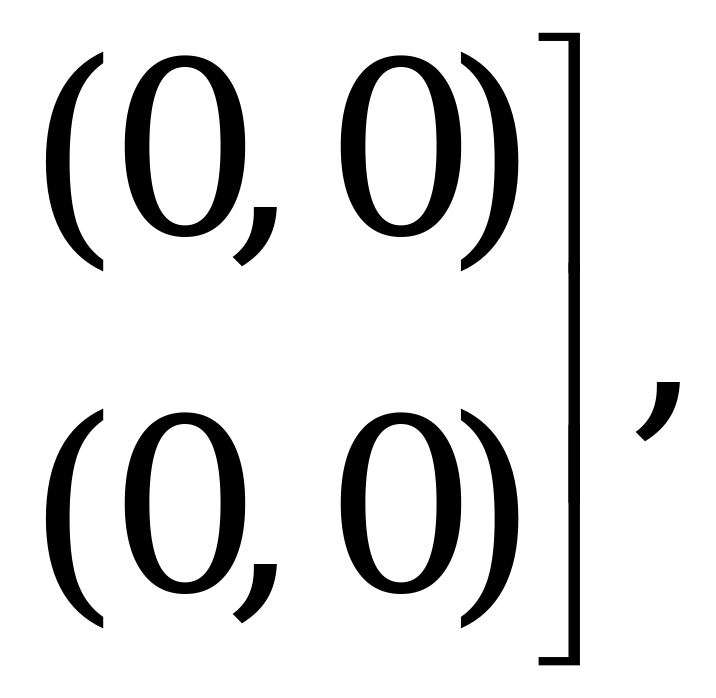
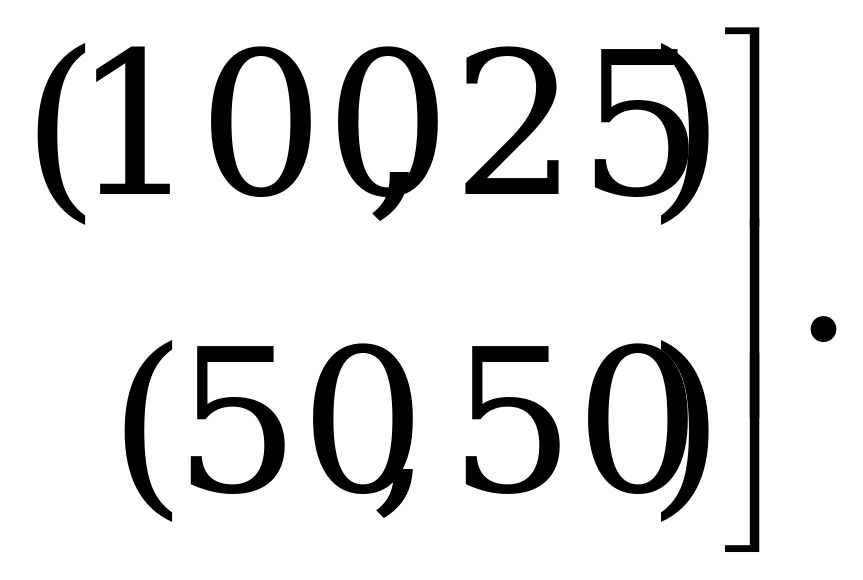
 ри этом игрок A стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, а игрок B выбирает стратегию, приводящую его к минимальному проигрышу.
ри этом игрок A стремится выбрать такую стратегию, которая доставляет ему максимальный выигрыш, а игрок B выбирает стратегию, приводящую его к минимальному проигрышу.



 ешение игры можно найти с помощью следующих построений.
ешение игры можно найти с помощью следующих построений.  налогично можно построить прямые
налогично можно построить прямые  ешение. Матрица имеет размерность 4×2, поэтому решение задачи находим для игрока
ешение. Матрица имеет размерность 4×2, поэтому решение задачи находим для игрока  сли в точке
сли в точке 



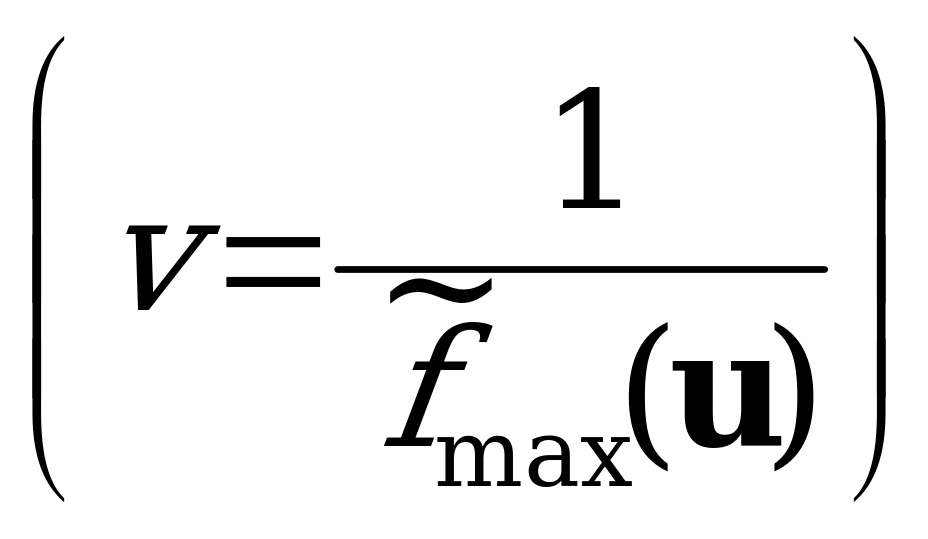 ,
, 











 2
2 2
2 чень важным преимуществом итерационного метода решения игр является то, что его трудоёмкость сравнительно медленно возрастает с увеличением размерности игры
чень важным преимуществом итерационного метода решения игр является то, что его трудоёмкость сравнительно медленно возрастает с увеличением размерности игры  2005 году Нобелевская премия по экономике присуждена Томасу Шеллингу и Роберту Ауманну за вклад в лучшее понимание конфликта и сотрудничества при помощи теории игр. Оба лауреата посвятили не один десяток лет теории игр и получили премию за анализ социальных проблем при помощи этой теории. При этом Ауманн занимался проблемой сотрудничества и конфликтов с точки зрения математики, а Шеллинг – с точки зрения экономики.
2005 году Нобелевская премия по экономике присуждена Томасу Шеллингу и Роберту Ауманну за вклад в лучшее понимание конфликта и сотрудничества при помощи теории игр. Оба лауреата посвятили не один десяток лет теории игр и получили премию за анализ социальных проблем при помощи этой теории. При этом Ауманн занимался проблемой сотрудничества и конфликтов с точки зрения математики, а Шеллинг – с точки зрения экономики.




















