Электронная презентация урока "Основные законы преобразования алгебры логики. Решение задач."

Основные законы преобразования алгебры логики

Решение задач

ЕАДК, преподаватель: Неверова И.Ю.

Задание 1. Для какого имени истинно высказывание:

¬(Первая буква имени гласная → Четвертая буква имени согласная)

1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР

Решение .

Введем обозначения для высказываний:

А = «Первая буква имени гласная» (з. 1 3)

В = «Четвертая буква имени согласная» (з. 1 4),

тогда наше высказывание примет вид: ¬( A → B ).

Чтобы преобразовать высказывание, воспользуемся тождествами (з.1, з.6, з.12):

з.1 з.6 з.12

¬( A → B ) = ¬((¬ A )  B ) = ¬(¬ A )  (¬ B ) = A  (¬ B )

Используя обозначения (з.13), (з.14), получим, что исходное высказывание равносильно следующему:

Первая буква гласная  ¬(Четвертая буква имени согласная), 

Первая буква гласная  Четвертая буква имени гласная.

Этому условию удовлетворяет только имя АНТОН (вариант ответа №3).

Ответ : 3 вариант

Задание 2.

Какое логическое выражение равносильно выражению ¬( A  ¬ B )

1) A  B 2) A  B 3) ¬ A  ¬ B 4) ¬ A  B Решение.

Чтобы преобразовать высказывание, воспользуемся законами (6), (12):

(6) (12)

¬( A  ¬ B ) = ¬ A  ¬(¬ B ) = ¬ A  B , что соответствует ответу №4.

Ответ : 4

Задание 3.

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X , Y , Z . Дан фрагмент таблицы истинности выражения F :

X

Y

0

0

0

Z

0

0

0

F

1

1

1

0

0

1

Какое выражение соответствует F?

1) ¬ X  ¬ Y  Z

2) ¬ X  ¬ Y  Z

3) X  Y  ¬ Z

4) X  Y  Z

Решение.

Способ 1. Наличие двух единиц в столбце F позволяет предположить использование дизъюнкции в логическом выражении. F принимает значение, равное 0, при X =0, Y =0, Z =1, что соответствует логической сумме X  Y  ¬ Z . При проверке этой формулы при значениях первой и третьей строки, получаем верные значения F .

Способ 2 . Проверим предложенные ответы:

F =¬ X  ¬ Y  Z =0 при X =0, Y =0, Z =0, что не соответствует первой строке таблицы.

F =¬ X  ¬ Y  Z =1 при X =0, Y =0, Z =1, что не соответствует второй строке таблицы.

Выражение X  Y  ¬ Z соответствует F при всех предложенных комбинациях X , Y , Z .

F = X  Y  Z =1 при X =0, Y =0, Z =1, что не соответствует второй строке таблицы.

Таким образом, верный вариант ответа №3.

Ответ : 3

1  ((X(15) 1) 1 2) 2 3) 3 4) 4 Решение. Заменим импликацию, входящую в исходное выражение, воспользовавшись тождеством (1): (1) ( X 5)→( X Подставим получившееся выражение в (15): ( X 1)  (( X1)  ( ¬ ( X= ( X 1)  ((X=5)  ( X (16) " width="640"

Задание 4.

Для какого числа X истинно высказывание:

X1  ((X

(15)

1) 1

2) 2

3) 3

4) 4

Решение.

Заменим импликацию, входящую в исходное выражение, воспользовавшись тождеством (1):

(1)

( X 5)→( X

Подставим получившееся выражение в (15):

( X 1)  (( X1)  ( ¬ ( X

= ( X 1)  ((X=5)  ( X

(16)

1)  ((1=5)  (1X =2: (21)  ((2=5)  (2X =3: (31)  ((3=5)  (3X =4: (41)  ((4=5)  (4Верный вариант ответа №2. Ответ : 2. " width="640"

Найдем значение выражения (16) при заданных значениях X (=1; 2; 3; 4)

X =1: (11)  ((1=5)  (1

X =2: (21)  ((2=5)  (2

X =3: (31)  ((3=5)  (3

X =4: (41)  ((4=5)  (4

Верный вариант ответа №2.

Ответ : 2.

Задание 5.

Укажите, какое логическое выражение равносильно выражению ¬(¬ A  B )

1) A  ¬ B 2) ¬ A  B 3) B  ¬ A 4) A  ¬ B

Решение.

Воспользуемся равенствами (6) и (12):

(6) (12)

¬(¬ A  B ) = ¬(¬ A )  ¬ B = A  ¬ B

Верный вариант ответа №1.

Ответ : 1

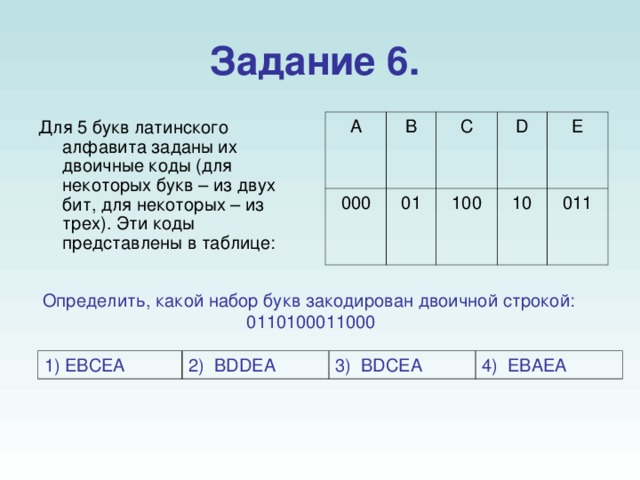
Задание 6.

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит, для некоторых – из трех). Эти коды представлены в таблице:

A

B

000

01

C

D

100

E

10

011

Определить, какой набор букв закодирован двоичной строкой: 0110100011000

1) EBCEA

2) BDDEA

3) BDCEA

4) EBAEA

Решение.

Заметим, что строка 0110100011000 может начинаться только с двух букв: 01(В) или 011(Е). При этом, если первая буква В, то для второй буквы имеется две возможности: 10( D ) и 101(-) – нет соответствующей буквы (см. Схему 1 ) и т.д.

При этом результативным является только одна ветвь дерева (на Схеме 1 она выделена двойной рамкой) – BDCEA , что соответствует варианту ответа №3.

Верный вариант ответа №3.

Ответ : 3.