Электронное пособие "Готовимся к ГИА 9 класс"

«Четырёхугольники»

• Четырёхугольник

• Параллелограмм

• Прямоугольник

• Ромб

• Квадрат

• Трапеция

• Вписанный и описанный четырёхугольники

А

Четырёхугольник – это многоугольник с четырьмя вершинами и четырьмя сторонами

• Соседние вершины – вершины, являющиеся концами одной из сторон четырёхугольника ( A, B )

• Противолежащие вершины – вершины не являющиеся соседними ( A, C )

• Диагонали четырёхугольника – отрезки, соединяющие противолежащие вершины ( BD ).

• Соседние стороны – стороны, исходящие из одной вершины ( AD, AB ).

• Противолежащие стороны – стороны, не являющиеся соседними ( AD, BC ).

• Периметр – сумма длин всех сторон четырёхугольника

P=AB+BC+CD+AD

В

D

С

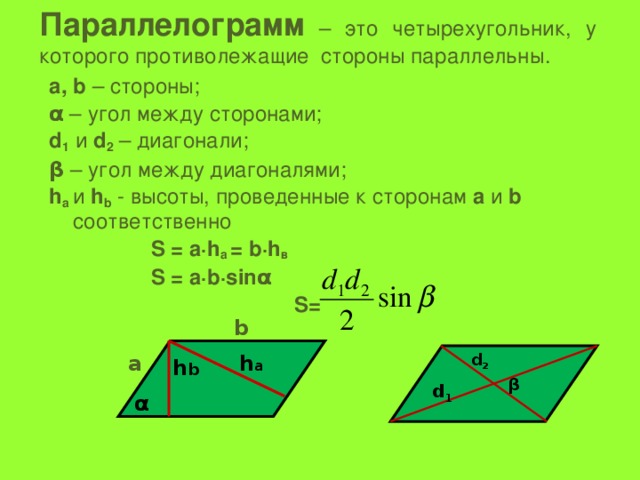
Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

а, b – стороны;

α – угол между сторонами;

d 1 и d 2 – диагонали;

β – угол между диагоналями;

h a и h b - высоты, проведенные к сторонам а и b соответственно

S = a·h a = b·h в

S = a·b·sinα

S=

b

h a

а

d 2

h b

β

d 1

α

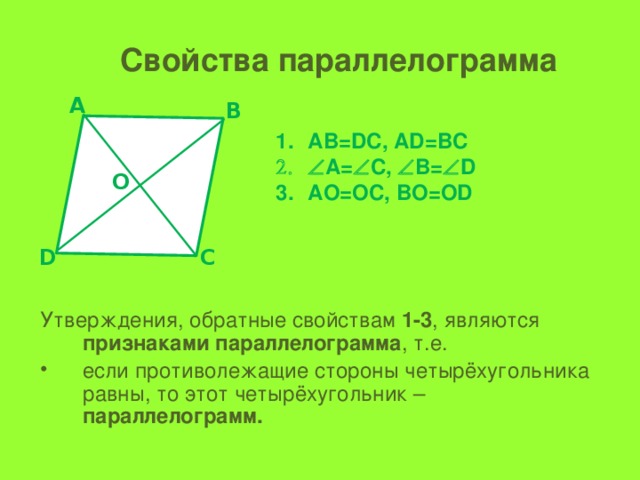
Свойства параллелограмма

A

B

• AB=DC, AD=BC
•  A=  C,  B=  D
• AO=OC, BO=OD

O

C

D

Утверждения, обратные свойствам 1-3 , являются признаками параллелограмма , т.е.

• если противолежащие стороны четырёхугольника равны, то этот четырёхугольник – параллелограмм.

Свойства параллелограмма

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон, т.е.

d 2

d 1

а

b

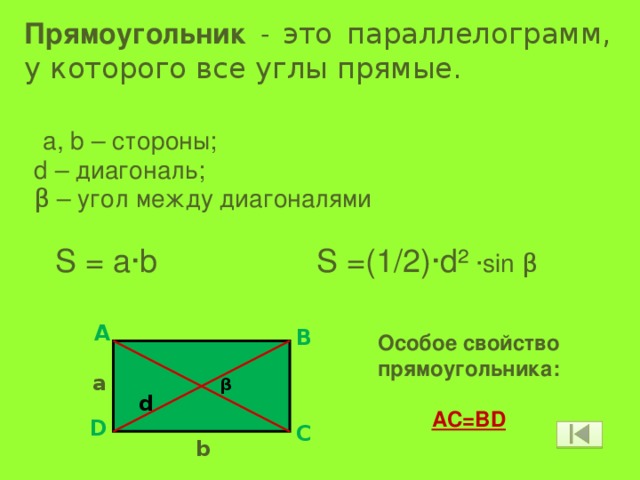
Прямоугольник - это параллелограмм, у которого все углы прямые.

а, b – стороны;

d – диагональ;

β – угол между диагоналями

S = a·b S =(1/2)·d² ·sin β

A

B

Особое свойство прямоугольника:

AC=BD

а

β

d

D

C

b

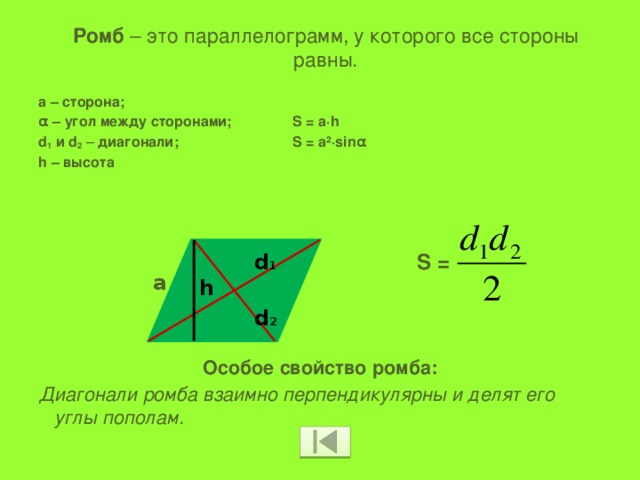
Ромб – это параллелограмм, у которого все стороны равны.

а – сторона;

α – угол между сторонами; S = a·h

d 1 и d 2 – диагонали; S = a²·sinα

h – высота

Особое свойство ромба:

Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

d 1

S =

а

h

d 2

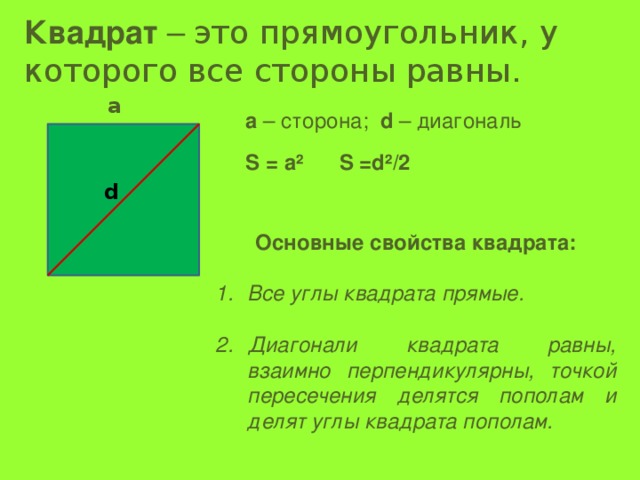
Квадрат – это прямоугольник, у которого все стороны равны.

а

а – сторона; d – диагональ

S = a² S =d²/2

d

Основные свойства квадрата:

• Все углы квадрата прямые.

• Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Свойства прямоугольника, ромба и квадрата

Для прямоугольника, ромба и квадрата справедливы все свойства параллелограмма.

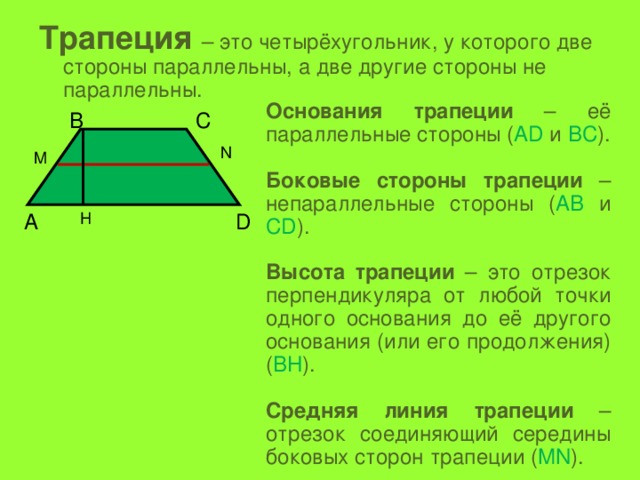
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Основания трапеции – её параллельные стороны ( AD и BC ).

Боковые стороны трапеции – непараллельные стороны ( AB и CD ).

Высота трапеции – это отрезок перпендикуляра от любой точки одного основания до её другого основания (или его продолжения) ( BH ).

Средняя линия трапеции – отрезок соединяющий середины боковых сторон трапеции ( MN ).

B

C

N

M

A

D

H

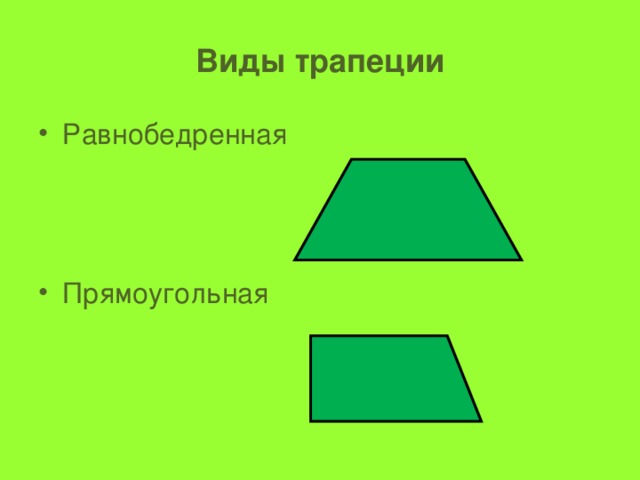
Виды трапеции

• Равнобедренная

• Прямоугольная

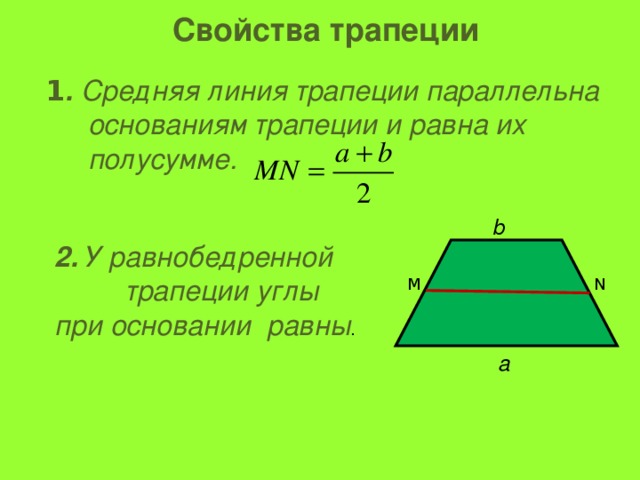
Свойства трапеции

1 . Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

b

2. У равнобедренной трапеции углы при основании равны .

M

N

a

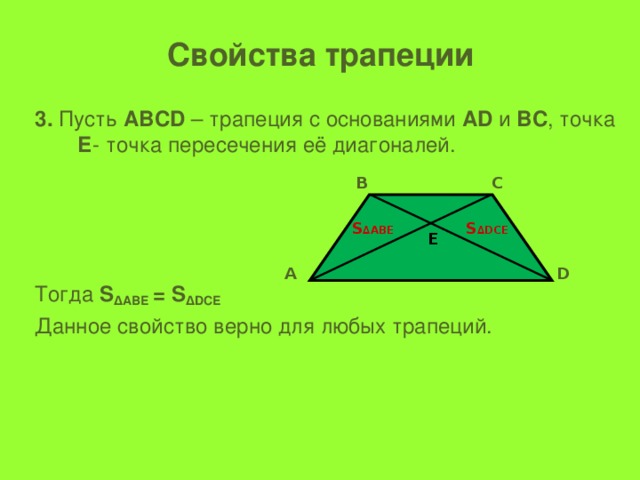
Свойства трапеции

3. Пусть АВСD – трапеция с основаниями АD и ВС , точка Е - точка пересечения её диагоналей.

Тогда S ∆АВЕ = S ∆DСЕ

Данное свойство верно для любых трапеций.

В

С

S ∆АВЕ

S ∆DСЕ

Е

D

А

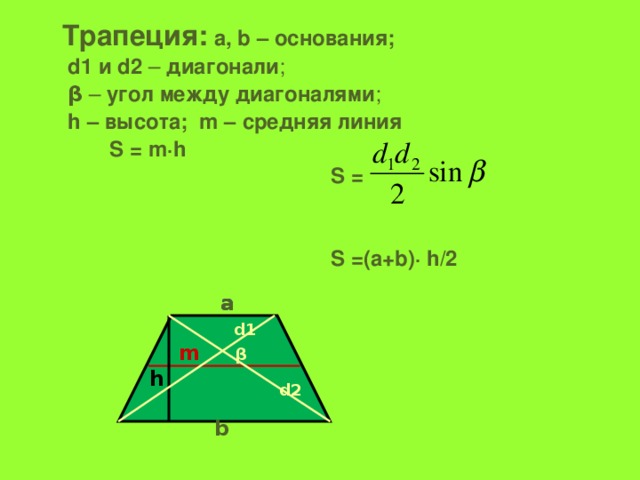
Трапеция: а, b – основания;

d1 и d2 – диагонали ;

β – угол между диагоналями ;

h – высота; m – средняя линия

S = m·h

S =

S =(а+b)· h/2

а

а

d1

m

β

h

d2

b

h

h

h

h

a

a

a

a

S = a x h

b

S =

a + b

x h

h

2

a

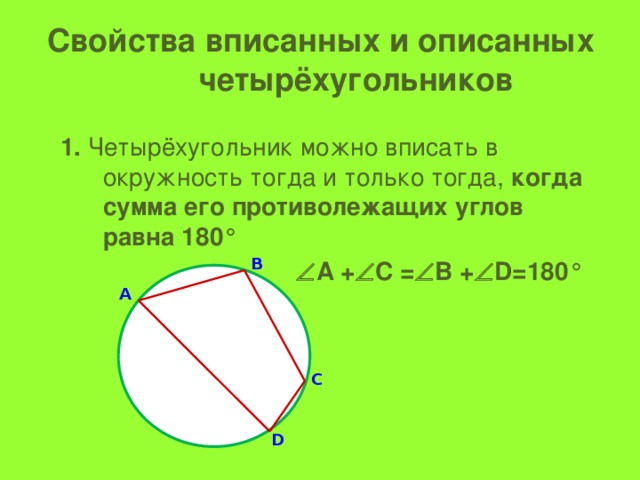
Свойства вписанных и описанных четырёхугольников

1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°

 А +  С =  В +  D=180°

В

А

С

D

16

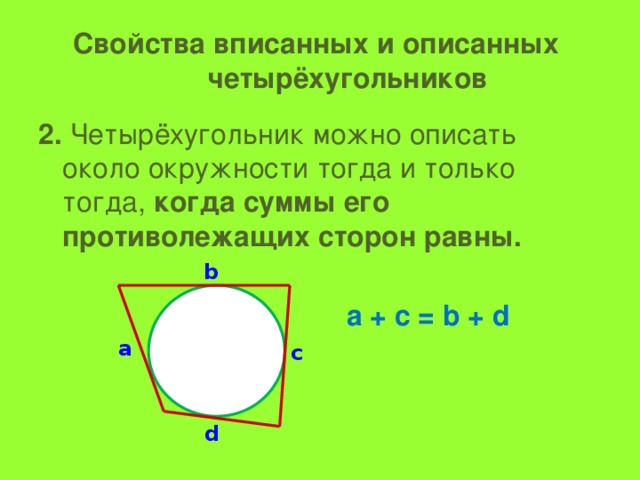
Свойства вписанных и описанных четырёхугольников

2. Четырёхугольник можно описать около окружности тогда и только тогда, когда суммы его противолежащих сторон равны.

а + с = b + d

b

а

с

d

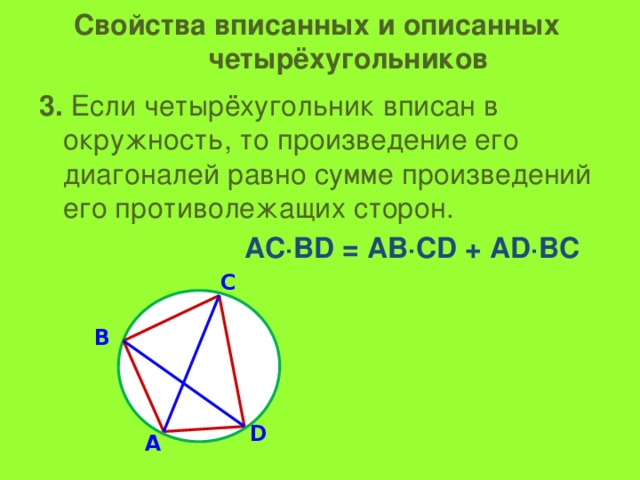
Свойства вписанных и описанных четырёхугольников

3. Если четырёхугольник вписан в окружность, то произведение его диагоналей равно сумме произведений его противолежащих сторон.

АС·ВD = АВ·СD + АD·ВС

С

В

D

А

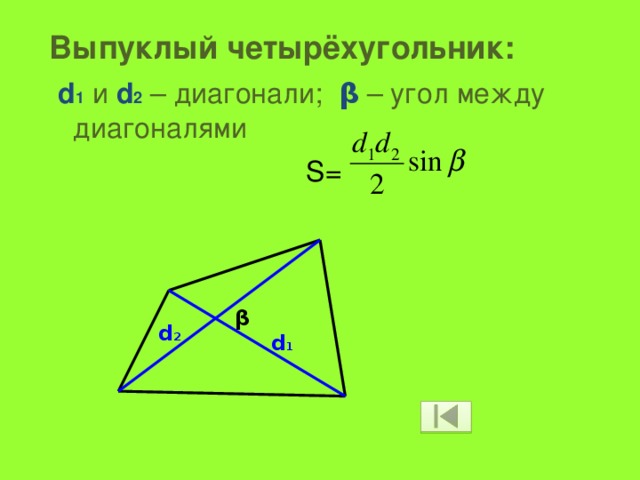
Выпуклый четырёхугольник:

d 1 и d 2 – диагонали; β – угол между диагоналями

S=

β

d 2

d 1