В механике под твердым телом понимают систему материальных точек, расстояние между любыми двумя точками которого в процессе движения остается неизменным.
Момент инерции – это величина, зависящая от распределения масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением
 ,
,
где - элементарные массы тела;
- элементарные массы тела; - их расстояния от оси вращения.
- их расстояния от оси вращения.
Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла
 , (1)
, (1)
где  – масса элемента тела, находящегося на расстоянии
– масса элемента тела, находящегося на расстоянии от интересующей нас оси. Интегрирование должно производиться по всему объему тела.
от интересующей нас оси. Интегрирование должно производиться по всему объему тела.
Вращение твердого тела вокруг неподвижной оси
Рассмотрим твердое тело массой  , вращающееся вокруг неподвижной оси с угловой скоростью
, вращающееся вокруг неподвижной оси с угловой скоростью . Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса”
. Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса”
 , (7)
, (7)
напомним, что в этом уравнении  и
и – момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело.
– момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело.
Момент импульса некоторой точки тела массой  вращающейся по окружности радиуса
вращающейся по окружности радиуса со скоростью
со скоростью , равен
, равен

Просуммировав по всему объему тела, учитывая, что  получим
получим

Таким образом, момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции тела относительно этой оси на его угловую скорость.
Подставляя полученное выражение в (7), получим уравнение динамики твердого тела, вращающегося вокруг неподвижной оси,
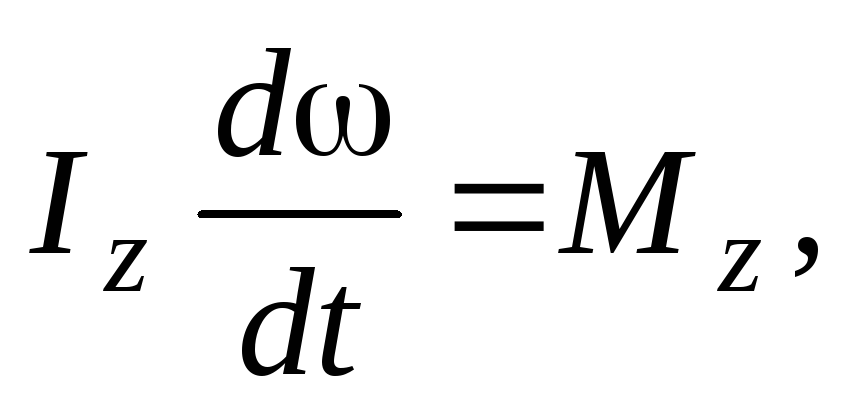 или
или  (8)
(8)
где  – угловое ускорение тела.
– угловое ускорение тела.
Найдем кинетическую энергию вращающегося тела. Для этого просуммируем по всему объему тела кинетические энергии отдельных его частей

или
 (9)
(9)
Зная зависимость момента сил, действующих на тело, от угла поворота, можно найти работу этих сил при повороте тела на конечный угол 
 .
.







 ,
, - элементарные массы тела;
- элементарные массы тела; - их расстояния от оси вращения.
- их расстояния от оси вращения. , (1)
, (1) – масса элемента тела, находящегося на расстоянии
– масса элемента тела, находящегося на расстоянии от интересующей нас оси. Интегрирование должно производиться по всему объему тела.
от интересующей нас оси. Интегрирование должно производиться по всему объему тела. , вращающееся вокруг неподвижной оси с угловой скоростью
, вращающееся вокруг неподвижной оси с угловой скоростью . Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса”
. Для того чтобы получить уравнение, описывающее это движение, применим уравнение моментов относительно оси, полученное в разделе “ Закон сохранения момента импульса” , (7)
, (7) и
и – момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело.
– момент импульса и момент силы относительно оси, вокруг которой вращается твердое тело. вращающейся по окружности радиуса
вращающейся по окружности радиуса со скоростью
со скоростью , равен
, равен
 получим
получим
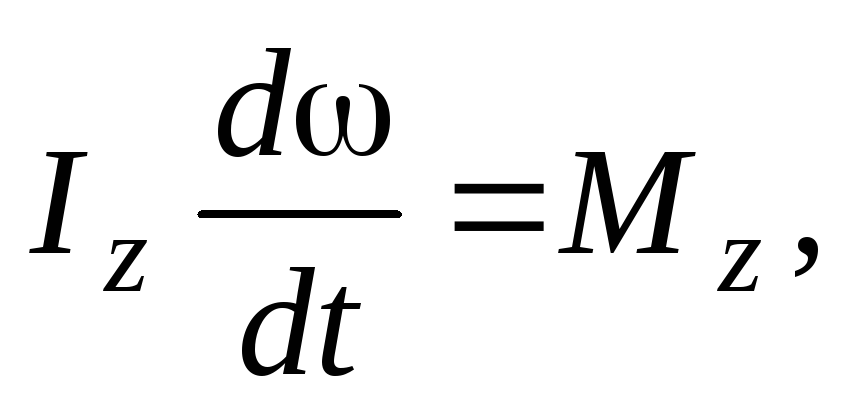 или
или  (8)
(8) – угловое ускорение тела.
– угловое ускорение тела.
 (9)
(9)
 .
.









