

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Формирование ИКТ-компетентности обучающихся на уроках геометрии
Просмотр содержимого документа
«Формирование ИКТ-компетентности обучающихся на уроках геометрии»
Формирование ИКТ-компетентности обучающихся на уроках геометрии
Оглавление
Введение …………………………………………………………………………..3
Общая характеристика Федерального стандарта образования………………...6
Психолого-педагогические аспекты использования информационных технологий на уроках математики……………………………………………...10
Обзор основных дидактических возможностей программы «Математический конструктор»……………………………………………………………………..16
Формирование и развитие ИКТ-компетентности на уроках геометрии при рассмотрении темы «Четырехугольники» …………………………………….27
Выводы…………………………………………………………………………...39
Список использованной литературы…………………………………………...41
ВВЕДЕНИЕ
Федеральный государственный образовательный стандарт (ФГОС) основного общего образования задал новые требования к результатам школьного образования, которые не могут быть достигнуты без организации активной учебной, практической, исследовательской, проектной деятельности учеников. Требования организации такой деятельности зафиксированы в Стандарте в том числе путем важного нововведения: наряду с традиционными учебными предметами в основной школе предполагается освоение обучающимися междисциплинарный учебных программ, результаты которых достигаются в ходе изучения всех учебных дисциплин [1]. Одной из таких междисциплинарных программ является программа «Формирование ИКТ-компетентности обучающихся», основные результаты освоения которой связаны с овладением обучающимися навыками обращения с устройствами ИКТ, фиксации изображений и звуков, создания письменных, музыкальных и звуковых сообщений, графических объектов с помощью специализированных компьютерных программ, создания и восприятия гипермедиасообщений и многое другое. Но отдельно хотелось бы обратить внимание на группу результатов по таким направлениям, как моделирование, проектирование и управление, анализ информации и математическая обработка данных в исследовании: среди этих результатов намечены такие, как умение строить математические модели изучаемых процессов и явлений, моделировать с использованием виртуальных конструкторов и проводить эксперименты и исследования в виртуальных лабораториях по математике и естественным наукам [2].
Вопрос о возможности достижения таких образовательных результатов напрямую связан с наличием, доступностью для образовательного учреждения и дидактическими возможностями специализированных компьютерных программ – интерактивных творческих предметных сред, ориентированных именно на работу с учащимися 5-9 классов в российской школе. За последние годы на рынке электронных средств обучения появилась интерактивная творческая среда – «1С:Математический конструктор» [3], которая представляет собой специализированное программное средство со своим интерфейсом, набором инструментов и функций, используемых как для разработки, так и для проигрывания готовых моделей.
Использование интерактивных творческих сред в основной школе позволяет достичь результатов междисциплинарной учебной программы «Формирование ИКТ-компетентности обучающихся», однако, не менее важным является тот факт, что разработанные с помощью конструкторов интерактивные модели различных процессов и явлений можно использовать для проведения учебного исследования на основе виртуального эксперимента, т.е. попутно достичь и результатов учебной программы «Основы учебно-исследовательской и проектной деятельности»: создание интерактивной модели с помощью конструктора включает в себя все основные этапы, свойственные научному исследованию – постановка задачи, математическая формализация, построение математической модели, реализация модели в конструкторе, проведение виртуального эксперимента и анализ полученных результатов.
Актуальность темы исследования в первую очередь связана с тем, что в последнее время накоплено большое количество компьютерных продуктов учебного назначения различной направленности и содержания, однако не существует методики их практического использования в школьном учебном процессе.
Создание методической базы для использования учебных компьютерных продуктов очень важно. В условиях модернизации образования, внедрения инновационных методов обучения, в частности, использования информационных технологий при изучении самых разных дисциплин, необходимо разрабатывать методику использования конкретных программ на уроках математики в школе. Это особенно актуально для геометрии в связи с важной ролью принципа наглядности обучения в рамках этой дисциплины. При этом ощущается острая нехватка методических материалов для учителя по использованию этой программы в условиях среднего образования. А отсутствие методических рекомендаций, учитывающих специфику конкретного раздела школьного курса геометрии и подготовку педагога, приводит к тому, что во многих школах они не востребованы.
Все вышесказанное обуславливает актуальность исследования как проблемы методики преподавания математики с использованием новых информационных технологий, в том числе компьютерных продуктов учебного назначения.[27]
ОБЩАЯ ХАРАКТЕРИСТИКА ФЕДЕРАЛЬНОГО СТАНДАРТА ОБРАЗОВАНИЯ
Федеральный государственный образовательный стандарт основного общего образования (далее – Стандарт) представляет собой совокупность требований, обязательных при реализации основной образовательной программы основного общего образования образовательными учреждениями, имеющими государственную аккредитацию[1].
Стандарт включает в себя требования:
к результатам освоения основной образовательной программы основного общего образования;
к структуре основной образовательной программы основного общего образования, в том числе требования к соотношению частей основной образовательной программы и их объёму, а также к соотношению обязательной части основной образовательной программы и части, формируемой участниками образовательного процесса;
к условиям реализации основной образовательной программы основного общего образования, в том числе к кадровым, финансовым, материально-техническим и иным условиям.
Математика и информатика
Изучение предметной области «Математика и информатика» должно обеспечить:
осознание значения математики и информатики в повседневной жизни человека;
формирование представлений о социальных, культурных и исторических факторах становления математической науки;
понимание роли информационных процессов в современном мире;
формирование представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.
В результате изучения предметной области «Математика и информатика» обучающиеся развивают логическое и математическое мышление, получают представление о математических моделях; овладевают математическими рассуждениями; учатся применять математические знания при решении различных задач и оценивать полученные результаты; овладевают умениями решения учебных задач; развивают математическую интуицию; получают представление об основных информационных процессах в реальных ситуациях.
Предметные результаты изучения предметной области «Математика и информатика» должны отражать:
Математика. Алгебра. Геометрия. Информатика:
1) формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления;
2) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) овладение символьным языком алгебры, приёмами выполнения тождественных преобразований выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умения моделировать реальные ситуации на языке алгебры, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат;
5) овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей;
6) овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего мира; развитие пространственных представлений, изобразительных умений, навыков геометрических построений;
7) формирование систематических знаний о плоских фигурах и их свойствах, представлений о простейших пространственных телах; развитие умений моделирования реальных ситуаций на языке геометрии, исследования построенной модели с использованием геометрических понятий и теорем, аппарата алгебры, решения геометрических и практических задач;
8) овладение простейшими способами представления и анализа статистических данных; формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о простейших вероятностных моделях; развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать массивы числовых данных с помощью подходящих статистических характеристик, использовать понимание вероятностных свойств окружающих явлений при принятии решений;
9) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах;
10) формирование информационной и алгоритмической культуры; формирование представления о компьютере как универсальном устройстве обработки информации; развитие основных навыков и умений использования компьютерных устройств;
11) формирование представления об основных изучаемых понятиях: информация, алгоритм, модель – и их свойствах;
12) развитие алгоритмического мышления, необходимого для профессиональной деятельности в современном обществе; развитие умений составить и записать алгоритм для конкретного исполнителя; формирование знаний об алгоритмических конструкциях, логических значениях и операциях; знакомство с одним из языков программирования и основными алгоритмическими структурами — линейной, условной и циклической;
13) формирование умений формализации и структурирования информации, умения выбирать способ представления данных в соответствии с поставленной задачей — таблицы, схемы, графики, диаграммы, с использованием соответствующих программных средств обработки данных;
14) формирование навыков и умений безопасного и целесообразного поведения при работе с компьютерными программами и в Интернете, умения соблюдать нормы информационной этики и права.
ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЕ АСПЕКТЫ ИСПОЛЬЗОВАНИЯ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ НА УРОКАХ МАТЕМАТИКИ
Понятие информационных образовательных технологий
Сегодня важной проблемой методики преподавания математики является проблема использования информационных технологий и компьютерных продуктов в обучении математике.
Под информационными технологиями понимается совокупность методов и технических средств сбора, организации, хранения, обработки, передачи и представления информации, расширяющая знания людей. В практической деятельности под информационными технологиями обучения понимаются все технологии, использующие специальные технические информационные средства.
Психологические аспекты использования информационных технологий на уроках математики
В последние годы в психологии выделились отдельные направления, связанные с широким применением компьютеров. В отечественной психологической науке появилось новое направление – психология компьютеризации, в основу которого легла выдвинутая О.К.Тихомировым [26] концепция преобразования мыслительной деятельности человека через компьютеры и другие средства информатики.
В задачи этого направления входят: изучение закономерностей и принципов организации различных видов человеческой деятельности, опосредствованной компьютерами, диалога между человеком и компьютером; изучение законов психического отражения и психического развития в условиях использования компьютеров, влияние компьютеризации на личность и личности на компьютеризацию и другие. Развитие этого направления позволило выявить ряд важных закономерностей психологии взаимодействия человека и ЭВМ.
Влияние компьютера на мотивацию учащихся и формирование у них познавательного интереса
Сторонники применения компьютерных технологий в учебном процессе считают, что использование компьютера повышает мотивацию к изучению предмета у учащихся за счет усиления как внешних, так и внутренних стимулов. Применение компьютера приводит к повышению активности учащегося, его стремления к принятию оптимальных решений, выдвижению гипотез и т.п. [18].
Многим ученикам придется в дальнейшем работать с компьютером в своей профессиональной деятельности, и это повышает их заинтересованность в использовании компьютерных программ учебного назначения на уроке и дома.
Психологические и медицинские (непсихологические) последствия применения информационных технологий
Данная проблема вызывает наибольшие опасения как у сторонников использования компьютеров в учебном процессе, так и у противников. В педагогической и психологической литературе имеется значительное количество публикаций, где подробно исследуется этот вопрос, выдвигаются медицинские и психологические требования к работе учеников за компьютерами [7].
Обязательно надо говорить об ограничении времени работы с компьютерными программами, так как иначе это может негативно сказаться на здоровье учащихся.
Зрительное напряжение у учащихся может быть вызвано как из-за несоответствия визуальных эргономических параметров дисплея (яркость, контрастность и т.д.), так и за счет неправильного расположения рабочих мест и освещения помещения. Необходимо отметить, что при постоянной работе за дисплеем у учащихся формируется нервно-психическое напряжение, а в ряде случаев развивается перенапряжение, которое рассматривается в качестве одной из причин невротических нарушений. При использовании компьютера в учебном процессе необходимо избегать возникновения подобных ситуаций, для чего рекомендуется менять режимы работы учащихся, формы и средства подачи учебного материала, перенося часть нагрузки со зрения на слух. Отметим, что в последнее время качество компьютерных дисплеев постоянно улучшается (в частности, появились жидкокристаллические мониторы практически не производящие вредных излучений), и если в середине 80-х гг. прошлого века время работы за компьютером даже для детей среднего и старшего школьного возраста было ограничено 15 минутами, то сейчас допустимая норма значительно выше.
Таким образом, по мнению ряда психологов, положительные результаты, достигнутые при работе с компьютером, повышают самооценку учащегося и уверенность в себе, способность решать более сложные творческие задачи. Из позитивного отношения к работе с компьютером складывается удовлетворенность учащегося, как на когнитивном, так и на эмоциональном уровне. Это приводит к формированию таких позитивных личностных черт, как точность и аккуратность.
Итак, растущее применение компьютеров во всех сферах человеческой деятельности порождает новые проблемы и дает толчок к развитию новых областей исследования. Изучение психологических и социальных аспектов взаимодействия человека и компьютера, а также поиск эффективных методов применения информационных технологий приобретают особую актуальность в настоящее время.
Педагогические условия использования информационных технологий на уроках математики
Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому предмету, их активность на протяжении всего урока. Использование компьютера при обучении позволяет создать информационную обстановку, стимулирующую интерес и пытливость ребенка.
В школе компьютер становится электронным посредником между учителем и учеником. Он позволяет организовать процесс обучения по индивидуальной программе. Ученик, обучающийся за пультом компьютера, может сам выбирать наиболее удобную для него скорость подачи и усвоения материала. В этом главное преимущество компьютера в процессе обучения: он позволяет работать с каждым учеником в отдельности [14].
Индивидуализация обучения улучшает качество подготовки. Это достигается за счет живой обратной связи, которая устанавливается в процессе диалога школьника с персональным компьютером (ПК). В зависимости от характера ответов на контрольные вопросы компьютер может предложить наводящие вопросы, подсказать или замедлить темп обучения. Если же ученик устанет, может предложить ему в качестве обучения развлекательно-обучающую программу.
Опыт использования ПК показывает, что машина позволяет освободить учителя от ряда утомительных функций, например, отработки элементарных умений и навыков, проверки знаний [22].
Целесообразно применять компьютер в следующих случаях:
1) диагностического тестирования качества усвоения материала;
2) в тренировочном режиме для отработки элементарных умений и навыков после изучения темы;
3) в обучающем режиме;
4) при работе с отстающими учениками, у которых применение компьютера обычно значительно повышает интерес к процессу обучения;
5) в режиме самообучения;
6) в режиме графической иллюстрации изучаемого материала.
Условно программное обучение можно классифицировать следующим образом:
1) обучающие программы;
2) контролирующие программы;
3) инструментальные программы.
В настоящее время многие школы оснащены прекрасными компьютерными классами. Однако следует заметить, что используется эта техника на уроках математики не так уж часто. Недостаток в программно-методических комплексах, включающих в себя компьютерную программу и пособие для учителя, которое содержит не только описание технических возможностей программы, но и поурочную разработку той или иной темы.
Программно-методические комплексы для уроков математики – просто редкость. Предполагается, что учитель сам должен придумать использование программного средства на уроке [13].
Появление ПК существенно влияет на программу школьного курса математики и методику ее преподавания. При организации учебного процесса и работе с компьютером необходимо учитывать индивидуальные особенности учащихся. Для одних работа с компьютером на уроке проста и естественна, а для других без постоянной поддержки и объяснений учителя затруднительна. При работе с ЭВМ необходима высокая концентрация внимания и высокая работоспособность пользователя, что является его индивидуальной характеристикой, так как высокая напряженность деятельности, монотонный, однородный характер изображений, навязчивость темпа работы, вызывает утомление и усталость. Все вышесказанное говорит о том, что компьютер на занятиях следует применять продуманно и осторожно, используя его только в тех случаях, когда с использованием компьютерных продуктов существенно увеличивается эффективность обучения.
Можно выделить следующие основные направления применения компьютерных продуктов и информационных технологий в процессе обучения математике в средней школе:
- при объяснении нового материала;
- при проведении лабораторных работ, и в частности, для самостоятельного эвристического поиска доказательств учащимися;
- для осуществления контроля знаний;
- при индивидуальной работе (программы-репетиторы, программы для творчества и самообразования) и самоподготовке;
- использование компьютерных продуктов учебного назначения (КПУН) для помощи учителю в подготовке к занятиям (электронные энциклопедии, офисные программы, генераторы задач и т.д.).
ОБЗОР ОСНОВНЫХ ДИДАКТИЧЕСКИХ ВОЗМОЖНОСТЕЙ ПРОГРАММЫ «МАТЕМАТИЧЕСКИЙ КОНСТРУКТОР»
«1С: Математический конструктор» – первая российская разработка мирового класса в области интерактивных динамических систем для школьников. Программная среда разработана с учетом требований, предъявляемых российской школой и российской традицией преподавания математики. Впервые уникальный опыт лучших педагогов-математиков и пожелания российских пользователей учитываются и используются отечественными разработчиками.
Программная среда «1С: Математический конструктор» предназначена для создания интерактивных моделей по математике, сочетающих в себе конструирование, моделирование, динамическое варьирование, эксперимент. Динамический наглядный механизм «Математического конструктора» предоставляет младшим школьникам возможность творческой манипуляции с объектами, а ученикам старшей школы – полнофункциональную среду для конструирования и решения задач.
Интерактивные динамические системы признаны во всем мире наиболее эффективным средством обучения математике с применением информационно-компьютерных технологий. В отличие от традиционного рисунка – геометрического чертежа или графика функции, выполненных на листе бумаги или с помощью «обычных» систем компьютерной графики, построение, созданное с помощью такой системы, – это модель, сохраняющая не только результат построения, но и его исходные данные, алгоритм и зависимости между объектами. При этом все данные легко доступны для изменения (можно перемещать мышью точки, варьировать размеры, вводить с клавиатуры новые значения числовых данных и т.п.). И эти изменения тут же, в динамике, отражаются на экране компьютера.
"1С: Математический конструктор 6.0" - это:
Динамические геометрические построения
Измерения и вычисления
Функции и графики
Конические сечения и другие кривые
Теория вероятностей и статистика
Области и операции над ними
Автоматическая проверка построений и тестовых заданий
Текстовый редактор с вводом формул
Анимация построений
Экспорт рисунков и апплетов
Гибкая настройка панелей инструментов в моделях
Интуитивно понятный интерфейс
Пользовательские инструменты и скрипты
Динамический наглядный механизм "Математического конструктора" предоставляет младшим школьникам возможность творческой манипуляции с объектами, а ученикам старшей школы - полнофункциональную среду для конструирования и решения задач.
Для ученика:
Коллекция интерактивных обучающих моделей
Создание аккуратных чертежей и графиков
Самостоятельное исследование и эксперимент
Для учителя:
Быстрое построение чертежей при работе на уроке
Организация проектной деятельности учащихся
Создание обучающих материалов и контрольных работ
Коллекция интерактивных моделей
К данному изданию "1С:Математического конструктора" прилагается "Коллекция моделей", содержащая 180 учебных модулей (около 280 отдельных моделей) с интерактивными заданиями и демонстрациями по всем разделам курса математики основной школы.
Состав "Коллекции" подбирался так, чтобы затронуть как можно более широкий спектр тем - с акцентом на те из них, в которых использование моделей конструктора в образовательных целях видится наиболее эффективным. В то же время разработчики стремились представить всевозможные типы учебных материалов, используемые на разных стадиях учебного процесса и при разных видах учебной деятельности. С точки зрения методики, предпочтение отдавалось материалам, которые можно использовать в рамках существующей системы преподавания по стандартным программам. При отборе моделей также ставилась цель продемонстрировать возможности программы.
В "Коллекции" пять частей: "Арифметика", "Алгебра", "Функции", "Геометрия", "Вероятность и статистика".
Представленные в издании модели можно открывать непосредственно или загрузить в систему организации учебного процесса "1С:Образование 5. Школа". Для этого на диске дополнительно размещены учебные модули, упакованные в zip-архивы и снабженные файлами манифеста и метаданных в соответствии со спецификациями Цифровых образовательных ресурсов (ЦОР).
Программная среда "1С:Математический конструктор" может использоваться как дома, так и в школе при различных формах проведения занятий и при различной компьютерной оснащенности учебного класса;
позволяет быстрее и эффективнее освоить школьный курс по математике, повышает запоминаемость материала;
обеспечивает возможность изучения математики на основе деятельностного подхода за счет внедрения элементов эксперимента и исследования в учебный процесс;
повышает степень эмоциональной вовлеченности учащихся в занятия математикой, обеспечивает возможность постановки творческих задач и организации проектной работы;
демонстрирует, насколько эффективно могут использоваться современные технологии для моделирования и визуализации математических понятий.
Технические особенности
Программная среда "1С:Математический конструктор"
позволяет работать на компьютерах под управлением операционных систем MS Windows, Linux, Mac OS;
обеспечивает экспорт создаваемых учебных моделей в виде интернет-совместимых java-апплетов, независимых от программы-редактора, но позволяющих использовать все возможности конструктивной среды;
допускает произвольное расширение возможностей конструктивной среды и учебных моделей за счет использования макросов и встроенного скриптового языка программирования (Java Script);
поддерживает спецификацию SCORM RTE для интеграции с системами управления учебным процессом (LMS).
Основные технические требования
Рекомендуемая конфигурация компьютера:
Windows 2000/XP/Vista/7/8; GNU Linux (ALT Linux, Ubuntu); Mac OS X
Pentium IV 2.0 ГГц, RAM 1024 Мб, HD 80 Мб
1024х768, true color
DVD-ROM
Java Runtime Environment (JRE) 7.0
Практическая апробация подтверждает: уже после краткого знакомства с программой учителя и ученики могут эффективно работать с «1С:Математическим конструктором» на уроках и дома. Можно указать три основных направления его использования в учебно-практической деятельности.
«Математический конструктор» – незаменимый помощник автора учебных материалов, в том числе учителя. В простейшем случае он позволяет легко создавать качественные рисунки для вставки в печатные тексты. Однако в полном объеме возможности конструктора раскрываются при создании интерактивных моделей-иллюстраций к объяснению теории и моделей-заданий, содержащих заготовки математических объектов, условия заданий и инструкции по работе с ними, пошаговые планы построений и т.п. информацию, а также, при необходимости, модуль проверки. При этом предусмотрена возможность создания полнофункциональных моделей, которые могут работать автономно от программы-конструктора.
Заранее подготовленные модели по конкретным вопросам учебной программы могут использоваться учителем и учениками на всех этапах занятий, в то числе, благодаря модулю проверки, и как задания для самостоятельных и контрольных работ. При этом ученики работают не с конструктором, а с автономными моделями.
«Математический конструктор» может служить инструментальной средой для самостоятельной работы учащихся на уроке (или дома) «с чистого листа». При этом перед учениками ставятся задачи построения и исследования определенных объектов, в ходе решения которых и должны достигаться те или иные учебные цели. Использование конструктора в таком качестве отвечает самым современным педагогическим концепциям. В то же время, такая форма занятий предполагает определенную перестройку учебного процесса, перенос акцентов на новые, современные формы работы, а в перспективе и подготовку новых учебников и пособий, рассчитанных на проектную, поисковую деятельность учащихся, сопровождаемую переподготовкой учителей.
Программная среда «1С:Математический конструктор»:
поддерживает автоматическую проверку построений, функций и графиков, символьных ответов и передачу оценки в электронный журнал современных систем управления учебным процессом, использующих спецификацию SCORM RTE;
имеет удобный, интуитивно понятный графический интерфейс, позволяет настраивать интерфейс создаваемых учебных моделей, в том числе ограничивать состав доступных инструментов;
обеспечивает экспорт создаваемых учебных моделей в виде интернет-совместимых java-апплетов, независимых от программы-редактора, но позволяющих использовать все возможности конструктивной среды;
обеспечивает кроссплатформенность, возможность работать с инструментальным комплексом на компьютерах под управлением различных операционных систем: Windows, Linux, MacOS;
допускает произвольное расширение возможностей конструктивной среды и учебных моделей за счет использования макросов и встроенного скриптового языка программирования[8]
Отметим, что независимые от основной программы модели-апплеты могут порождаться и в других программах динамической геометрии. Важнейшее отличие моделей «Математического конструктора» состоит в том, что в них могут быть заложены любые инструменты и команды полной версии программы, включая инструменты построений, а не только возможность передвижения элементов чертежа.
Потребность сопроводить задачу иллюстрацией – одна из наиболее простых, но и наиболее часто возникающих на практике. В чем преимущество использования «Математического конструктора» для рисования таких иллюстраций?
Чертеж, построенный в «Математическом конструкторе», принципиально отличается от чертежа, нарисованного в графическом редакторе, который при изменении одного элемента автоматически изменяет и элементы, с ним связанные – перпендикуляр к прямой останется перпендикуляром, биссектриса угла – биссектрисой, вписанная окружность – вписанной и т.д. Это свойство динамических чертежей открывает безграничный простор для разнообразных применений. О некоторых из них и идет речь ниже.
В качестве примера можно рассмотреть иллюстрацию к теореме об окружности девяти точек. Построить этот, не столь уж простой чертеж с помощью коллекции «Мои инструменты» «Математического конструктора» – дело нескольких минут, и, что самое важное, при этом мы можем подобрать такую форму исходного треугольника, при которой четко видны все 9 рассматриваемых точек – такой чертеж можно вставлять в печатный документ.
Приведенная модель не только дает хороший чертеж, но и позволяет экспериментально убедиться в справедливости теоремы, варьируя треугольник, а также показывает построение по шагам, и может быть использована на уроке.
Разумеется, при изучении геометрии не всегда нужно выполнять чертеж тщательно, доказательства можно проводить и при помощи эскизов, выполненных палочкой на песке. И все же удобный инструмент для создания аккуратных геометрических чертежей, которые порой способны подсказать ученику путь решения задачи, помешать не может.

Рис. 1. Интерактивная модель «Окружность девяти точек»
При создании статичных чертежей специфические возможности «Математического конструктора» используются лишь в небольшой степени. Мы уже отметили ключевую особенность построений в среде динамической геометрии: любые чертежи в «Математическом конструкторе», в отличие от начерченных на бумаге или на классной доске, относятся не к индивидуальной геометрической фигуре, а к целому непрерывному семейству фигур.
Ученика вряд ли удивит, что при деформации треугольника луч, построенный как биссектриса его угла, всегда будет делить этот угол пополам – ведь именно так он и построен. Но если провести все три биссектрисы, то мы увидим, что они будут всегда пересекаться в одной точке, хотя эту точку мы и не строили – она возникла «сама». А это уже маленькое геометрическое открытие!
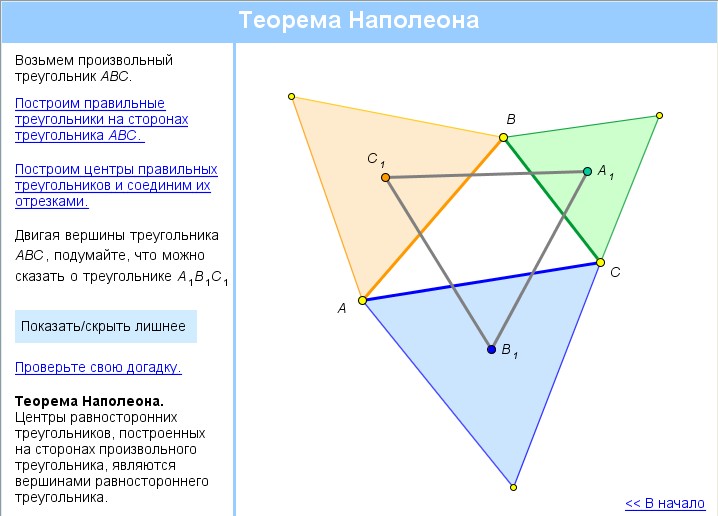
Рис. 2. Интерактивная модель «Теорема Наполеона»
И такое открытие может перевернуть весь ход урока – от заунывного изложения «фактов», пусть даже сопровождаемого пассивным иллюстрированием, вы переходите к активному стимулированию творческого потенциала учеников, развиваете в них навык видеть, формулировать и понимать геометрические закономерности, существенно увеличиваете степень эмоциональной вовлеченности и запоминаемость изучаемого материала. Вот более сложная модель такого типа.
Все расстояния, углы и площади в «Математическом конструкторе» легко измеряемы. Это позволяет проводить численные экспериментальные наблюдения, которые могут вести к самостоятельному открытию тех или иных фактов.

Рис. 3. Интерактивная модель «Сумма расстояний до сторон равностороннего треугольника»
Важнейшим классом учебных заданий, формируемых при помощи «Математического конструктора», являются задачи на конструирование с помощью предоставляемого ученику набора виртуальных инструментов. В частности, любая «классическая» школьная задача на построение циркулем и линейкой может быть представлена в интерактивной компьютерной форме. Причем как на итоговом чертеже, так и на всех промежуточных фазах решения важную роль играет возможность проверки правильности построения вариацией данных – когда кажущийся «правильным» чертеж рассыпается при деформировании исходных объектов, если он был создан лишь визуально похожим рисованием, а не геометрически корректным построением. Выполнив построение, ученик имеет возможность исследовать условия существования решения и зависимость числа решений от данных задачи.
Задачи на построение могут быть снабжены автоматической проверкой решения: если требуемая фигура имеется на чертеже, то при нажатии на кнопку «Проверить» появляется сообщение о выполнении задания. Аналогичное сообщение может передаваться и в программную оболочку, формирующую оценку. Неверные или неполные ответы можно снабжать реакциями-комментариями.
Более того, «Математический конструктор» позволяет не только проверять ответ, но и снабжать неверные или неполные ответы реакциями-комментариями.
Богатые методические возможности предоставляет инструментарий, позволяющий создавать управляемые пошаговые сценарии работы с многоуровневыми заданиями.
Очень полезны, например, динамические чертежи с визуальными подсказками. На этих чертежах часть информации, играющая роль подсказки, поначалу спрятана. Доступ к подсказке может быть как прямым (вызов ссылкой-кнопкой), так и требовать от пользователя предварительного выполнения каких-либо действий (например, введения ответа). Подсказкой может быть дополнительное построение, значение какой-то величины, анимированное преобразование фигуры и т.д. Важно, что подсказки носят невербальный характер и тем самым развивают геометрическое воображение, интуицию, умение воспринимать по-разному представленную информацию [7].
ФОРМИРОВАНИЕ И РАЗВИТИЕ ИКТ-КОМПЕТЕНТНОСТИ НА УРОКАХ ГЕОМЕТРИИ ПРИ РАСМОТРЕНИИ ТЕМЫ «ЧЕТЫРЕХУГОЛЬНИКИ»
Развитие электронных средств наглядности привело к закреплению ведущей роли интерактивных моделей, которые позволяют производить различные манипуляции с геометрическим чертежом. При подготовке таких учебных материалов важно использовать алгоритм построения, обеспечивающий наиболее широкие возможности учителю для работы с геометрическими объектами.
Конкретное содержание интерактивной модели, а также способ ее подготовки (последовательность и методы построения) зависит от целей, которые преследует учитель. В связи с этим рассмотрим методические аспекты подготовки и использования в обучении геометрии динамических чертежей, создаваемых в программе «Математический конструктор».
При этом будем придерживаться концепции, согласно которой использование различных средств электронной наглядности на уроке математики должно быть дозированным, нельзя заменить аналитическую работу учащихся просматриванием анимационных геометрических картинок. Представляется целесообразным занимать не более 30-50% процентов учебного времени работе со средствами компьютерных технологий (в среднем), возможно, эта цифра должна быть еще меньше.
Каждая интерактивная модель с заложенными в нее дидактическими возможностями может быть описана следующими компонентами:
- начальное содержание (геометрические и вспомогательные объекты) с описанием технологии построения (использования конкретных инструментов программы и последовательность построения);
- типовая схема манипуляций с объектами, вынесенными на модель, и соответствующий перечень понятий (свойств, вопросов), которые рекомендуется рассмотреть с учащимися.
В соответствии с таким подходом разработка модели к уроку может выполняться в следующей последовательности:
- определение перечня и последовательности понятий и свойств, которые необходимо (желательно) проиллюстрировать и обсудить с учащимися;
- определение текстовых материалов (например, определение геометрической фигуры), которые целесообразно разместить на модели и определение геометрических объектов, которые должны сразу присутствовать на модели;
- определение манипуляций с различными объектами на модели в соответствии с перечнем понятий и свойств, которые необходимо проиллюстрировать;
- описание дидактических возможностей модели при самостоятельной работе учащихся с ней.
Кроме этого не следует преувеличивать значение конкретного разъяснения, конкретной единичной педагогической ситуации на уроке, ведь без самостоятельной работы учащихся по соответствующей теме самые выдающиеся объяснения могут не обеспечить достижение дидактических целей.
Рассмотрим в соответствии с приведенным описанием интерактивную модель по теме «Определение четырехугольника»1, основное назначение которой – наглядное сопровождение при объяснении нового материала, но при этом она может быть использована и для самостоятельной работы учащихся.
1. Определим перечень и последовательность понятий и свойств, которые необходимо (желательно) проиллюстрировать и обсудить с учащимися: - определение четырехугольника: четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющихся отрезков;
- названия элементов четырехугольника:
* вершины, соседние вершины, противолежащие вершины;
* стороны, соседние стороны, противолежащие стороны;
* диагонали;
- при этом необходимо обратить внимание на то, что:
* если какие-нибудь три или больше вершин лежат на одной прямой, то это уже не четырехугольник;
* если какие-нибудь стороны пересекаются, то это не четырехугольник;
- понятие выпуклого и невыпуклого четырехугольника;
- обратить внимание на установление связи между понятием четырехугольника, выпуклого четырехугольника и взаимным расположением его элементов.
2. Определим текстовые материалы, которые целесообразно разместить на модели и геометрические объекты, которые должны сразу присутствовать на ней:
- название модели: определение четырехугольника (необходимо добавить текстовое поле на рабочую область, ввести и отформатировать текст);
- произвольный четырехугольник (воспользоваться инструментом Построить многоугольник).

Рис. 1. Начальная конфигурация модели «Определение четырехугольника»
3. Определим манипуляции с различными объектами на модели в соответствии с перечнем понятий и свойств, которые необходимо проиллюстрировать.
3.1. Познакомить учащихся с определением четырехугольника, ввести понятие вершин, соседних и противолежащих вершин, сторон, соседних и противолежащих сторон.
3.2. Построить прямую, проходящую через любые две соседние вершины, например АВ.
3.3. Переместить точку С (или точку D) так, чтобы отрезок CD пересекал отрезок АВ (рис. 2). При этом отметить – полученная фигура четырехугольником не является.
|
|
|
| Рис. 2 | Рис. 3 |
3.4. Переместить точку С на прямую АВ (рис. 3). При этом отметить, что полученная фигура – треугольник АСD.
3.5. Переместить точку С так, чтобы СD пересекал прямую АВ за точкой В (рис. 4) – получили невыпуклый четырехугольник. Можно пояснить: если прямая, проходящая через любые соседние вершины четырехугольника не пересекает другие его стороны, то четырехугольник – выпуклый, в противном случае – не выпуклый.
|
|
|
| Рис. 4 | Рис. 5 |
3.6. Провести отрезки АС и BD – сообщить, что они называются диагоналями четырехугольника, выделить их цветом и сделать полужирными (рис. 5).
3.7. Перемещая точку С (рис. 6-9) попросить учащихся сделать вывод о зависимости наличия пересечения диагоналей и вида геометрической фигуры (не является четырехугольником, является невыпуклым четырехугольником, является выпуклым четырехугольником). Школьники сделают вывод: четырехугольник является выпуклым только если диагонали пересекаются.
|
|
|
| Рис. 6 | Рис. 7 |
|
|
|
| Рис. 8 | Рис. 9 |
Очевидно, что данная модель (позволяющая свободно перемещать вершины фигуры, выполнять дополнительные построения и производить выделение цветом и другими средствами отдельные элементы фигур) дает возможность учителю полностью раскрыть существенное содержание понятия четырехугольника.
4. Опишем дидактические возможности модели при самостоятельной работе учащихся с ней [7].
При описании основных возможностей программы ранее уже было указано, что созданные в «Математическом конструкторе» интерактивные модели доступны для работы в автономном режиме, без установки самой программы на компьютер. В связи с этим посредством интернет сайта школы или, записывая на флэш накопители, можно готовые интерактивные модели в виде Java апплетов передавать школьникам для самостоятельной работы с ними дома. При регулярности такой работы учащиеся свободно смогут выполнять построения в программе, т.к. она снабжена большим количеством готовых инструментов: построение отрезка, прямой, луча, окружности по разным элементам и т.д. Обратная связь с учителем может быть осуществлена следующим образом:
- учащиеся выполняют задание в апплете;
- нажав кнопку PrintScreen скопировать полученное ими изображение в графический редактор MS Paint и сохранить в файле;
- файл можно переслать учителю по электронной почте или распечатать изображение и принести на урок (возможно в электронном виде).
Многие авторы отмечают, что просто необходимо предлагать школьникам пользоваться самыми современными способами передачи информации, иначе учащиеся будут не готовы к профессиональной деятельности в современном информационном обществе. В связи с этим, описанный метод организации обратной связи в современной (даже провинциальной России) является оправданным и целесообразным.
Рассмотрим задание, которое можно предложить учащимся для самостоятельной работы с апплетом. При этом предполагается что на апплете доступны инструменты: построение точек, построение отрезков и прямых. Также с апплета можно удалить все первоначально присутствующие объекты.
1. Переместить вершины так, чтобы получился невыпуклый четырехугольник.
2. Переместить вершины так, чтобы получилась фигура, не являющаяся четырехугольником.
3. Построить четырехугольник с параллельными противолежащими сторонами (кто-то построить трапецию, кто-то параллелограмм).
4. Построить четырехугольник с равными сторонами.
5.Предложите свои частные случаи расположения вершин четырехугольника, выделите свойства, которыми обладает построенная вами фигура.
Такое задание можно считать не обязательным, дополнительным. Мотивировать учащихся к выполнению таких заданий можно разными способами, в частности отмечать публично наиболее интересные работы, в которых присутствует творческое начало. В таком случае выполнять такие дополнительные задания учащимся будет престижно. Учителю при такой мотивации необходимо опираться на поощрение, а не на наказание и выставление двоек. Кроме этого считаем, что использование компьютера при выполнении заданий по математике само по себе является достаточно интересной (в каком-то смысле игровой) деятельностью для учеников.
Рассмотрим методику применения программы при изучении темы «Средняя линия треугольника» и доказательстве соответствующей теоремы. Воспользуемся предложенной выше схемой описания применения модели в учебном процессе.
1. Определим перечень и последовательность понятий и свойств, которые необходимо (желательно) проиллюстрировать и обсудить с учащимися.
1.1. Понятие средней линии треугольника: средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
1.2. Теорема о средней линии треугольника: формулировка и доказательство. Причем свойства средней линии учащиеся должны сформулировать сами до сообщения формулировки теоремы учителем. Ход доказательства теоремы также должен быть предложен учащимися при рассмотрении динамической модели.
1.3. Типовая задача: доказать, что середины сторон произвольного четырехугольника являются вершинами параллелограмма. Ход доказательства учащиеся должны предложить сами.
2. Определим текстовые материалы, которые целесообразно разместить на модели и геометрические объекты, которые должны сразу присутствовать на ней (рис. 10).
2.1. На начальную конфигурацию целесообразно поместить название модели - Средняя линия треугольника и определение этого понятия.
2.2. Из геометрических объектов в первую очередь необходимо расположить произвольный треугольник АВС.

Рис. 10. Начальная конфигурация модели «Средняя линия треугольника»
2.3. Для работы с теоремой необходимо предварительно заготовить ее формулировку – создать соответствующее текстовое поле. Отображать формулировку целесообразно по нажатию кнопки Теорема, после того, как различные манипуляции с треугольником АВС позволят учащимся самостоятельно сформулировать основные положения теоремы (целесообразно использовать кнопку Показать/Скрыть в меню Кнопки).
2.4. Для рассмотрения основной задачи желательно заранее подготовить соответствующий чертеж – произвольный четырехугольник, с отмеченными серединами сторон М1, М2, М3 и М4, которые соединены отрезками – получен параллелограмм. Данный чертеж целесообразно отображать по нажатию кнопки Чертеж к основной задаче. Условие задачи, вынесенной на текстовое поле также желательно отображать по нажатию соответствующей кнопки Условие задачи. Это связано с тем, что при выполнении манипуляций с чертежом к задаче учащиеся могут сами сформулировать утверждение, которое требуется доказать.
3. Определим манипуляции с различными объектами на модели в соответствии с перечнем понятий и свойств, которые необходимо проиллюстрировать.
3.1. Сообщить тему и озвучить определение средней линии треугольника. Построить середины сторон АВ и ВС – точки МС и МА (воспользоваться инструментом Разделить отрезок пополам). Задать учащимся вопрос: сколько у треугольника средних линий? При необходимости можно построить середину третьей стороны и построить все средние линии. Для работы с теоремой о средней линии треугольника надо оставить только одну среднюю линию МАМС, остальные линии можно скрыть (не удалять).
|
|
|
| Рис. 11 | Рис. 12 |
3.2. Следующий шаг – подвести учащихся к формулировке теоремы о средней линии треугольника. Первое свойство – параллельность средней линии основанию треугольника легко проиллюстрировать, если просто перемещать вершины треугольника. Задать вопрос учащимся: какое свойство средней линии можно заметить при изменении положения вершин треугольника? Чтобы наглядно проиллюстрировать равенство средней линии половине основания треугольника необходимо отобразить измерения соответствующих отрезков (рис. 12). Для этого просто выделяется отрезок и выбирается команда Расстояние между точками в меню Вычисления. Перемещая вершину С и останавливаясь при АС = 6, АС = 7 и т.д. можно спросить у учащихся: как связаны между собой длина средней линии и длина основания? Учащиеся обязательно ответят правильно на вопрос. Результат можно дополнительно проиллюстрировать, если вынести на чертеж отношение длин этих отрезков (рис. 13). Сделать это можно с помощью команды Частное в меню Вычисления: выбрать команду и показать последовательно мышью на текстовое окно с длиной первого и второго отрезков. При этом произвольное перемещение любых элементов треугольника будет оставлять неизменным указанное отношение. После получения ответов учащихся можно сформулировать теорему и отобразить ее условие, нажав на кнопку Теорема.
|
|
|
| Рис. 13 | Рис. 14 |
3.3.Следующий шаг – подтолкнуть учащихся к идее доказательства теоремы. Для этого необходимо сделать дополнительное построение: провести прямую через точку МА параллельно стороне АВ (рис. 14) и построить точку пересечения основания АС и построенной прямой – точку Е. Учащимся можно задать вопрос: что за фигура АМСМАЕ? При этом произвольно перемещать вершины треугольника. Будет получен ответ: параллелограмм. Следующий вопрос: если АМСМАЕ – параллелограмм, то какое утверждение теоремы это доказывает? Ответ: параллельность средней линии и основания треугольника. Следующий вопрос: как доказать, что ![]() ? Дальнейшие рассуждения: АМСМАЕ – параллелограмм, значит
? Дальнейшие рассуждения: АМСМАЕ – параллелограмм, значит ![]() , осталось показать, что Е – середина АС. Это следует из теоремы Фалеса. Дальше целесообразно сообщить схему доказательства: дополнительное построение и ссылка на теорему Фалеса доказывает требуемое утверждение (не обязательно ссылаться на то, что АМСМАЕ – параллелограмм).
, осталось показать, что Е – середина АС. Это следует из теоремы Фалеса. Дальше целесообразно сообщить схему доказательства: дополнительное построение и ссылка на теорему Фалеса доказывает требуемое утверждение (не обязательно ссылаться на то, что АМСМАЕ – параллелограмм).
3.4. Затем можно перейти к задаче. Сначала отображаем чертеж, нажав на кнопку Чертеж к основной задаче. Перемещая вершины четырехугольника АВСD можно спросить учащихся: какой фигурой является М1М2М3М4? Ответ: параллелограмм. Затем нажать на кнопку Условие задачи и отобразить текст. Дополнительное построение: построить прямую АС (рис. 15) и ссылка на то, что М1М2 – средняя линия треугольника АВС, М3М4 – средняя линия треугольника АСD доказывает параллельность М1М2 и М3М4. Остальные рассуждения выполняются по аналогии.
|
|
|
| Рис. 15 | Рис. 16 |
4. Опишем дидактические возможности модели при самостоятельной работе учащихся с ней.
- Предложить учащимся самостоятельно построить чертеж к задаче, но так, чтобы четырехугольник АВСD был прямоугольником. Какой фигурой является четырехугольник, соединяющий середины сторон (рис. 16)? Для построения прямоугольника можно воспользоваться командой Прямоугольник с горизонтальной стороной в меню Построения в подменю Многоугольники.
- Рассмотреть другие частные случаи четырехугольника АВСD, отметить наиболее интересные выводы.
План урока, на котором применяются информационные технологии обучения, имеет свои специфические особенности и отличается от обычного урока с традиционными средствами обучения. Учителю необходимо определить место, количество и способ предъявления учебной информации, которая будет предъявляться с помощью образовательных программных средств, четко сформулировать учебные цели использования компьютерного продукта, продумать дополнительные вопросы и выделить фрагменты, которые будут изучаться учащимися самостоятельно.
ВЫВОДЫ
В ходе исследования можно сделать вывод, что методически грамотное использование подготовленными учителями информационных технологий и качественных электронных учебных материалов позволит повысить эффективность процесса обучения учащихся геометрии и, следовательно, качество их знаний.
Занятия с использованием компьютерных продуктов учебного назначения позволяют:
1. реализовывать принципы индивидуального и дифференцированного подхода в процессе обучения;
2. реально готовят учащихся к работе в современных условиях и к жизни в информационном обществе;
3. развивают у учащихся образное и пространственное мышление; освобождают учителя от рутинной работы;
4. оказывают помощь учителю в организации действенного систематического контроля и обеспечивают объективную оценку деятельности учащихся;
5. воспитывают у учащихся аккуратность и внимательность, помогают формированию логического мышления и развитию памяти;
6. активизируют познавательную деятельность учащихся, позволяя выйти на более высокий уровень восприятия и усвоения изученного материала.
Методически оправданное использование учителями компьютерных продуктов учебного назначения на различных этапах учебного процесса позволяет существенно повысить эффективность усвоения учащимися учебного материала, позволяет включить у учеников различные формы восприятия учебной информации, повышает их познавательную активность, развивает творческие способности. Проверка знаний с использованием компьютерных продуктов учебного назначения позволяет выставлять более объективную оценку и снижает у ученика страх допустить ошибку и боязнь самого учителя.
Но для того, чтобы учителя могли действительно использовать существующие компьютерные программы по их предмету, а при необходимости и желании – создавать собственные продукты, необходимо поставить вопрос о подготовке учителя-предметника, способного к самообучению, владеющего основными навыками использования ИКТ, знающего психолого-педагогические аспекты применения компьютерной техники, умеющего творчески применять компьютер на уроке.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Федеральный государственный образовательный стандарт // http://standart.edu.ru/catalog.aspx?CatalogId=2588.
Примерная основная образовательная программа образовательного учреждения. Основная школа / [сост. Е.С. Савинов]. – М.: Просвещение, 2011. http://standart.edu.ru/catalog.aspx?CatalogId=6400.
Толковый словарь терминов понятийного аппарата информатизации образования. – М.: ИИО РАО, 2009. – 96 с.
Ваграменко Я.А. Информационные технологии и модернизация образования // Педагогическая информатика. – 2000. – № 2. – С.3-9.
Васильева И.А., Осипова Е.М., Петрова Н.Н. Психологические аспекты применения информационных технологий // Вопросы психологии. – 2002. – №3. – С.80-88.
Далингер В.А. Новые информационные технологии в обучении геометрии. – В кн.: Новые исследования в педагогических науках. Вып.1 – М.: Педагогика, 1991. – С.39.
Деркач Д.В. Использование программы «Математический конструктор» в обучении геометрии. / Современные образовательные технологии обучения математике и информатике в высшей и средней школе [Текст]: материалы IV Всероссийской научно-практической конференции (г. Армавир, 30-31 марта) – Армавир: РИЦ АГПУ, 2010. – С.9-11.
Дубровский В.Н., Лебедева Н.А., Белайчук О.А. 1С:Математический конструктор - новая программа динамической геометрии // Компьютерные инструменты в образовании. - СПб.: Изд-во ЦПО "Информатизация образования", 2007. №3. - С. 47-56.
Живая геометрия. Учебно-методическое пособие / Под ред. Шабат Г.Б. – М.: Институт новых технологий образования, 2001. – 239 с.
Информационные технологии в образовании: Учеб. пособие для студ. высш. учеб. заведений / И.Г. Захарова. – 3-е изд., стер. – М.: Издательский центр «Академия», 2007. – 192 с.
Кизилова В.П. Применение информационных технологий при обучении математике в профильной школе // Философия образования. – 2006. – №3. – С.295-299.
Киселева М.М. Использование компьютерных технологий в межпредметных проектах //Информатика и образование. – 2005. – № 8. – С. 27-38.
Компьютерная математика //Математика в школе. – 2006.– №6. – С.15-17.
Лабутин В.Б. Аспекты применения информационных технологий в образовательном процессе // Стандарты и мониторинг в образовании. – 2003. – №4. – 62 с.
Левитас Г.Г. Нетрадиционное преподавание геометрии с опорой на традиционный учебник // Математика в школе. – 2006. – №9. – С.54-57.
Максимова В.Н. Межпредметные связи и совершенствование процесса обучения: Кн. для учителя. – М.: Просвещение, 1984.
Манвелов С.Г. Основы творческой разработки урока математики // Математика. – 1997. – № 11, 13, 19, 21, 29.
Манвелов С.Г. Современный урок математики: Основы методики проведения // Математика. – 1998. – № 36, 37, 38, 41, 43
Мартиросян Л.П. Информационные технологии в обучении математике // Информатика и образование. – 2004. – № 6. – С.89-93.
Мартиросян Л.П. Реализация возможностей информационных технологий в процессе преподавания математики // Информатика и образование. – 2009. – № 4. – С.78-82.
Монахов В.М. Перспективы разработки и внедрения новой информационной технологии обучения на уроках математики // Математика в школе. – 1991. – № 3. – С.58-62.
Никифорова М.А. Преподавание математики и новые компьютерные технологии // Математика в школе. – 2005.– № 6. – С.73-80.
Погорелов А.В. Геометрия: Учеб. пособие для 7 – 11 кл. общеобразоват. учреждений. – М.: Просвещение, 1995. – 383 с.
Семенов А.Л. Роль информационных технологий в общем среднем образовании // Информатика и образование .– 2001. – № 2. – С.3-7.
Совертков П.И. Исследовательская деятельность в развивающих программах по информатике и математике // Информатика и образование. – 2003. – № 4. – С.11-17.
Тихомиров О.К. Основные психолого-педагогические проблемы компьютеризации обучения // Вопросы психологии. – 1986. – №4. – С.67-69.
Чернецкая Т.А. Реализация межпредметных связей математики, физики и информатики на основе использования в учебном процессе конструктивных творческих сред / Информатика и образование, 2013. - №2. – С. 79-83.
Фридман Л.М. Психолого-педагогические основы обучения математике в школе. – М.: Просвещение, 1983.– 160 с.
1 Изложение материала предлагается в соответствии с учебником Погорелов А.В. Геометрия 7-11.
44




























