Формирование вычислительных навыков у младших школьников с ограниченными возможностями здоровья в инклюзивной практике

 ФОРМИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ У МЛАДШИХ ШКОЛЬНИКОВ С ОГРАНИЧЕННЫМИ ВОЗМОЖНОСТЯМИ ЗДОРОВЬЯ В ИНКЛЮЗИВНОЙ ПРАКТИКЕ

Аннотация: В главе раскрыты теоретические основы формирования вычислительных навыков у младших школьников. Представлены результаты эксперимента по формированию вычислительных навыков у младших школьников с ограниченными возможностями здоровья в условиях инклюзивной практики.

Ключевые слова: младшие школьники с ограниченными возможностями здоровья, учащиеся с нарушением интеллекта, формирование, вычислительные приемы, умения и навыки.

Формирование у учащихся младших классов вычислительных навыков остаётся одной из главных задач начального обучения математике. В век компьютерных технологий значимость навыков письменных вычислений, несомненно, уменьшилась. Вместе с тем, научиться быстро и правильно выполнять письменные вычисления важно для младших школьников как в плане продолжающейся работы с числами при изучении арифметических действий, так и в плане практической значимости этих навыков для дальнейшего обучения в школе.

Трудности усвоения письменных вычислений обусловлены тем, что у детей быстро развивается усталость при работе с числами. Это объясняется большим количеством операций как письменного сложения и вычитания, так и письменного умножения и деления. Избежать быстрой утомляемости и снижения внимания при изучении письменных вычислений поможет чередование различных видов деятельности, отказ от однообразных тренировочных упражнений, внедрение проблемных заданий. Действие контроля должно присутствовать на каждом этапе выполнения вычислительного приёма. Любой вычислительный прием можно представить в виде последовательности операций, выполнение каждой из которых связано с определенным математическим понятием или свойством [4].

Основой вычислительных приемов при сложении и вычитании являются знания, умения и навыки, которые дети усваивают при изучении нумерации (принцип образования натурального ряда чисел, разрядный состав числа) [4].

Раскроем суть вычислительного приёма. Предположим, надо сложить числа 8 и 6. Приём вычисления для этого случая будет состоять из ряда операций:

1) замена числа 6 суммой удобных слагаемых 2 и 4;

2) прибавление к числу 8 слагаемого 2;

3) прибавление к полученному результату, к числу 10, слагаемого 4.

Здесь выбор операций и порядок их выполнения определяется соответствующей теоретической основой приёма – применением свойства прибавления к числу суммы (сочетательное свойство): замена числа 6 суммой удобных слагаемых, затем прибавление к числу 8 последовательно каждого слагаемого. Кроме того, здесь используются и другие знания, например, при выполнении первой операции используется знание состава чисел первого десятка: 10 = 8 + 2 и 6 = 2 + 4.

Из этого следует, что приём вычисления над данными числами складывается из ряда последовательных операций, выполнение которых приводит к нахождению результата требуемого арифметического действия над этими числами; причём выбор операций в каждом приёме определяется теми теоретическими положениями, которые используются в качестве теоретической основы [5].

В большинстве случаев уже в начальных классах школы для нахождения результата арифметического действия можно использовать в качестве теоретической основы различные теоретические положения, что приводит к разным приёмам вычислений.

Например:

15 ∙ 6 = 15 + 15 + 15 + 15 + 15 + 15 = 90;

15 ∙ 6 = (10 + 5) ∙ 6 = 10 ∙ 6 + 5 ∙ 6 = 90;

15 ∙ 6 = 15 ∙ (2 ∙ 3) = (15 ∙ 2) ∙ 3 = 90.

Теоретической основой для выбора операций, составляющих первый из приведённых приёмов, является конкретный смысл действия умножения; теоретической основой второго приёма – свойство умножения суммы на число, а третьего приёма – свойство умножения числа на произведение. Операции, составляющие приём вычисления, имеют разный характер. Многие из них сами являются арифметическими действиями. Эти операции играю особую роль в процессе овладения вычислительными приёмами: выполнение приёма в свёрнутом плане сводится к выделению и выполнению именно операций, являющихся арифметическими действиями. Поэтому операции, являющиеся арифметическими действиями, можно назвать основными. Например, для случая 16  4 основными будут операции: 10  4 = 40, 6  4 = 24, 40 + 24 = 64. Все другие операции – вспомогательные [5].

Число операций, составляющих прием, определяется, прежде всего, выбором теоретической основы вычислительного приема. Например, при сложении чисел 57 и 25 в качестве теоретической основы может выступать свойство прибавления суммы к числу, тогда прием будет включать три операции: замена числа 25 суммой разрядных слагаемых 20 и 5, прибавление к числу 57 слагаемого 20 и прибавление к результату, к 77, слагаемого 5; если же теоретической основой является свойство прибавления суммы к сумме, то прием для того же случая будет включать пять операций: замена числа 75 суммой разрядных слагаемых 50 и 7, замена числа 25 суммой разрядных слагаемых 20 и 5, сложение чисел 7 и 5, сложение полученных результатов 70 и 12. Число операций зависит также от чисел, над которыми выполняются арифметические действия.

Число операций, выполняемых при нахождении результата арифметического действия, может сокращаться по мере овладения приемом. Например, для случаев вида 8 + 2 на начальной стадии формирования навыка ученик выполняет три операции: замена числа 2 суммой 1 и 1, прибавление числа 1 к 8, прибавление числа 1 к результату, к 9. Однако после заучивания таблицы сложения ученик выполняет одну операцию – он сразу связывает числа 8 и 2 с числом 10. Как видим, здесь прием как бы перерастает в другой.

Общеизвестно, что теоретической основой вычислительных приёмов служат определения арифметических действий, свойства действий и следствия, вытекающие из них. Имея это в виду и принимая во внимание методический аспект, можно выделить группы приёмов в соответствии с их общей теоретической основой. Существуют различные классификации вычислительных приёмов. Рассмотрим более детально классификацию вычислительных приёмов, предложенную М. А. Бантовой, основанием которой является общность теоретической основы вычислительных приёмов, изучаемых в начальных классах [4].

Как видим, все вычислительные приёмы строятся на той или иной теоретической основе, причём в каждом случае учащийся осознает сам факт использования соответствующих теоретических положений, лежащих в основе вычислительных приёмов. Это реальная предпосылка овладения учащимися осознанными стойкими и обобщёнными вычислительными умениями и навыками.

Вычислительное умение представляет собой развернутое осуществление действия, в котором каждая операция осознается и контролируется [4]. В отличие от умения навыки характеризуются свернутым, в значительной мере автоматизированным выполнением действия, с пропуском промежуточных операций, когда контроль переносится на конечный результат.

Вычислительный навык – это высокая степень овладения вычислительными приёмами. Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения. Они входят в структуру учебно-познавательной деятельности и существуют в учебных действиях, которые выполняются посредством определенной системы операций. Приобрести вычислительные навыки, значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро [4].

Полноценный вычислительный навык обучающихся характеризуется следующими показателями: правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом и прочностью [4].

О правильности вычислительных навыков мы можем говорить, когда ученик правильно находит результат арифметического действия над данными числами, т. е. правильно выбирает и выполняет операции, составляющие прием.

Осознанность вычислительных навыков характеризуется тем, что обучающийся осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательство правильности выбора системы операции. Осознанность проявляется в том, что ученик в любой момент может объяснить, как он решал пример и почему можно так решать. Это, конечно, не значит, что ученик всегда должен объяснять решение каждого примера. В процессе овладения навыком объяснение должно постепенно свертываться.

О рациональности вычислительных навыков мы можем судить в случае, если ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный прием, т. е. выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату арифметического действия. Разумеется, что это качество навыка может проявляться тогда, когда для данного случая существуют различные приемы нахождения результата, и ученик, используя различные знания, может сконструировать несколько приемов и выбрать более рациональный. Как видим, рациональность непосредственно связана с осознанностью навыка.

Обобщенность вычислительных навыков характеризуется тем, что школьник может применить прием вычисления к большему числу случаев, т. е. он способен перенести прием вычисления на новые случаи. Обобщенность так же, как и рациональность, теснейшим образом связана с осознанностью вычислительного навыка, поскольку общим для различных случаев вычисления будет прием, основа которого – одни и те же теоретические положения.

Об автоматизме (свернутости) вычислительных навыков мы можем говорить, когда учащийся выделяет и выполняет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операции. Осознанность и автоматизм вычислительных навыков не являются противоречивыми качествами. Они всегда выступают в единстве: при свернутом выполнении операции осознанность сохраняется, но обоснование выбора системы операции происходит свернуто в плане внутренней речи. Благодаря этому ученик может в любой момент дать развернутое обоснование выбора системы операции. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям (5 + 3, 8 – 5, 9 + 6, 15 – 9, 7 – 6, 42 : 6). Здесь должен быть достигнут уровень, характеризующийся тем, что ученик сразу же соотносит с двумя данными числами третье число, которое является результатом арифметического действия, не выполняя отдельных операций. По отношению к другим случаям арифметических действий происходит частичная автоматизация вычислительных навыков: ученик предельно быстро выделяет и выполняет систему операций, не объясняя, почему выбрал эти операции и как выполнял каждую из них.

О прочности вычислительных навыков мы можем говорить, когда ученик сохраняет сформированные вычислительные навыки на длительное время.

Обобщая вышеизложенное, мы можем констатировать, что вычислительный навык определяется высокой степенью овладения вычислительными приемами и характеризуется правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом и прочностью.

В ряде исследований, раскрываются основные положения системы формирования вычислительного навыка. Особое внимание этому было уделено в работе М. А. Бантовой [4, 5].

Исходя из программных требований в начальном курсе математики учащиеся должны усвоить на уровне навыка:

– таблицу сложения и вычитания в пределах 10;

– таблицу сложения однозначных чисел с переходом через разряд и соответствующие случаи вычитания;

– таблицу умножения и соответствующие случаи деления.

Усвоение этих таблиц должно быть доведено до автоматизма. Иначе школьники будут испытывать трудности при овладении различными вычислительными умениями, в каждое из которых в качестве операций входят вычислительные навыки.

В основе формирования вычислительных навыков на уроках математики у младших школьников лежит осознанное и прочное усвоение приемов устных и письменных вычислений. Прочное владение вычислительными навыками, в том числе и умение применять их на практике – это фундамент изучения математики и других школьных дисциплин. Поэтому очень важно научиться быстро и правильно владеть вычислительными навыками еще в младших классах.

Для формирования любого навыка, в том числе и вычислительного, используются два подхода, которые в дальнейшем будут условно называться прямым и косвенным. Прямой подход характеризуется наличием готового образца выполнения изучаемой операции и большим количеством готовых тренировочных упражнений, в процессе выполнения которых ученики овладевают навыком на основе репродуктивной деятельности, где владение навыком выступает как самоцель по принципу «решай, чтобы научиться решать» [1].

Главным преимуществом здесь является очень быстрое достижение требуемого результата, поэтому он так широко распространен и занимает прочные позиции в школьной практике. Однако несомненны и отрицательные стороны. Сам подход к формированию вычислительного навыка за счет упражнений, выполняемых именно для того, чтобы научиться их выполнять, мы считаем противоестественным – так как человек овладевает технической стороной любого дела не как самоцелью, а ради решения актуальных для него задач. За исключением случаев, когда люди получают удовольствие от самого процесса выполнения арифметических действий, вычисления служат инструментом решения существенных проблем математики как учебного предмета или практических задач, возникающих в жизни. Длинная череда однообразных по своей сути тренировочных упражнений искажает суть математики, подменяя ее чередой однотонных и скучных действий, и, в конечном счете, вызывает отвращение к этой области знаний. Преобладание репродуктивной деятельности в формировании вычислительных навыков значительно сдерживает возможность продвижения детей в развитии, а в настоящее время развитие школьников является приоритетной задачей обучения в любой системе.

Важнейшей особенностью косвенного подхода к формированию навыков являются отсутствие готового образца выполнения операции, которой предстоит овладеть, самостоятельный поиск способов ее выполнения учащимися, что сразу включает их в продуктивную творческую деятельность [1].

Такой подход характеризуется высокой эффективностью процесса формирования навыка, полноценным осознанием теоретических и практических знаний, лежащих в основе алгоритмов выполнения вычислительных операций, повышением интереса к математике. При этом большая часть заданий позволяет получить обширный тренировочный материал для формирования навыка.

Недостатком является заметное увеличение времени, затрачиваемого на достижение результата.

Почему же система предпочитает именно косвенный подход к формированию навыков? Дело в том, что практически любое задание по любому учебному предмету, в том числе и по математике, должно способствовать продвижению детей в развитии, а прямой подход полностью исключает этот компонент. Если бы выработка навыков занимала небольшое учебное время, с этим можно было бы смириться, но это отнюдь не так: выполнение арифметических действий в любом классе начальной школы занимает в общей сложности почти его половину.

В большинстве случаев уже в начальных классах школы для нахождения результата арифметического действия можно использовать в качестве теоретической основы различные положения, что приводит к разным приёмам вычислений.

Вместе с тем, учитывая, что ученик при выполнении вычислительного приёма должен отдавать отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом – системой операций, мы относим к основным критериям и степень овладения умением контролировать себя при выполнении вычислительного приёма [1].

О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции, приводящие к решению.

В качестве еще одного показателя полноценного вычислительного навыка выделяют контроль. При этом необходимо отметить, что контроль – качественно иной показатель, чем перечисленные выше, а поэтому, его не следует рядополагать с ними. Умение осознанно контролировать выполняемые операции, позволяет формировать вычислительный навык на более высоком уровне, чем без наличия этого умения. Это значит, что все ранее раскрытые нами качественные характеристики, проявляются при формировании вычислительного навыка на более высоком уровне. Как видим, умение контролировать себя в процессе формирования вычислительного навыка требует от ученика полноценного, осознанного, обобщённого и самостоятельного владения всеми операциями, определяющими процесс выполнения вычислительного приёма [5].

В ходе формирования вычислительных умений и навыков у учащихся младших классов М. Н. Бантова выделяет следующие этапы.

1 этап. Подготовка к введению нового приёма.

На этом этапе создается готовность к усвоению вычислительного приёма, а именно, учащиеся должны усвоить те теоретические положения, на которых основывается приём вычислений, а также овладеть каждой операцией, составляющей приём.

Например, можно считать, что ученики подготовлены к восприятию вычислительного приёма ± 2, если они ознакомлены с конкретным смыслом действий сложения и вычитания, знают состав числа 2 и овладели вычислительными навыками сложения и вычитания вида ± 1; готовностью к введению приёма внетабличного умножения (13 × 6) будет знание учащимся правила умножения суммы на число, знание десятичного состава чисел в пределах 100 и овладение навыками табличного умножения, навыками умноженная числа 10 на однозначные числа, навыками сложения двузначных чисел.

Центральное звено при подготовке к введению нового приёма – овладение учеником основными операциями.

2 этап. Ознакомление с вычислительным приёмом.

На этом этапе ученики усваивают суть приёма, какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия.

При введении большинства вычислительных приёмов важно использовать наглядность. В некоторых случаях это оперирование множествами. Например, прибавляя к 6 число 3, придвигаем к 6 квадратам 3 квадрата по одному.

В других случаях в качестве наглядности используется развернутая запись. Например, при введении приёма внетабличного умножения выполняется запись: 13 × 6 = (10 + 3) × 6 = 10 × 6 + 3 × 6 = 60 + 18 = 78.

Выполнение каждой операции важно сопровождать пояснениями вслух. Сначала эти пояснения выполняются под руководством учителя, а потом самостоятельно учащимися.

3 этап. Закрепление знаний приёма и выработка вычислительного умения и навыка.

На этом этапе ученики должны твердо усвоить систему операций, составляющие приём, и быстро выполнить эти операции; то есть овладеть вычислительным навыком [4, 5].

В процессе работы здесь важно предусмотреть этапы в становлении у учащихся вычислительных умений и навыков:

1. На первом этапе закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производя развернутую запись:

34 × 5 = (30 + 4) × 5 = 30 × 5 + 4 × 5 = 3 × 10 × 5 + 20 = 3 × 5 × 10 + 20 = 15 × 10 + 20 = 150 + 20 = (100 + 50) + 20 = 100 + (50 + 20) = 100 + 70 = 170.

2. На втором этапе происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции и обосновывают выбор, порядок их выполнения, вслух же они проговаривают выполнение основных операций, т. е. промежуточных вычислений. Надо учить детей выделять основные операции в каждом вычислительном приёме. Развёрнутая запись не выполняется. Сначала проговаривание ведётся под руководством учителя, а затем самостоятельно. Проговаривание вслух помогает выделить основные операции, а выполнение про себя вспомогательных операций способствует их свертыванию (34 × 5 = (30 + 4) × 5 = 30 × 5 + 4 × 5 = 150 + 20 = 170).

3. На третьем этапе происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, т.е. здесь происходит свёртывание и основных операций. Учитель предлагает детям выполнять про себя и промежуточные вычисления, а называть или записывать только окончательный результат (34 × 5 = 170).

4. На четвёртом этапе наступает предельное свёртывание выполнения операций. Учащиеся выполняют все операции в свёрнутом плане, предельно быстро, т. е. они овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений [6].

Таким образом, на всех этапах формирования вычислительного умения и навыка решающую роль играют задания на применение вычислительных приёмов, причём содержание заданий должно подчиняться целям, которые ставятся на соответствующем этапе. Важно, чтобы было достаточное число заданий, чтобы они были разнообразными как по форме, так и по числовым данным. Надо иметь в виду, что свёртывание выполнения операций не у всех учащихся происходит одновременно, поэтому важно время от времени возвращаться к полному объяснению и развёрнутой записи приёма. Продолжительность каждого этапа определяется сложностью приёма, подготовленностью учащихся, и целями, которые ставятся на каждом этапе. Правильное выделение этапов позволит учителю управлять процессом усвоения учащимися вычислительного приёма, постепенного свёртывания выполнения операций, образования вычислительных навыков.

Однако у учеников, у которых процессы свёртывания выполнения арифметических операций оказываются недостаточно сформированными, появляются серьёзные трудности в овладении вычислительными навыками. Это касается, в первую очередь, категории школьников с ограниченными возможностями здоровья.

Проведенный нами анализ по выявлению у младших школьников с ограниченными возможностями здоровья (категория детей с нарушением интеллекта) особенностей и основных трудностей усвоения письменных вычислений свидетельствует о недостаточной сформированности у них понятий о числе, счёте, десятичной системе счисления, умений выполнять вычислительные приемы. В связи с чем, встаёт проблема поиска путей повышения эффективности обучения вычислительным приемам и формирования стойких и осознанных вычислительных навыков у младших школьников с ограниченными возможностями здоровья, а конкретно у категории детей, имеющих нарушение интеллекта.

Проведенное нами исследование было направлено на совершенствование методики обучения вычислительным приемам и формирования вычислительных навыков у учащихся данной категории на примере чисел четвертого концентра (нумерации и действий сложения и вычитания чисел в пределах 1000).

Определяя пути повышения эффективности обучения детей с нарушением интеллекта нумерации чисел в пределах 1000, мы предположили, что объяснение данной темы целесообразно осуществлять с использованием методических подходов и дидактического материала М. Монтессори («Золотой жемчужный материал», рис. 1).

Рисунок 1 – «Золотой жемчужный материал».

Упражнения с «Золотым жемчужным материалом» позволяют сформировать у ребенка чувственные образы математических категорий в окружающем мире, создать конкретную основу для абстрактных понятий. Они помогают ему самостоятельно, через деятельность с предметами, дойти до сути математических операций и постепенно перевести их из внешнего во внутренний план. В этом смысле работа с данным материалом не самоцель, а средство закономерного перехода к математическим абстракциям [2, 3, 7, 8].

«Золотой жемчужный материал», как и многие другие математические материалы М. Монтессори, четко показывает связь между алгеброй и геометрией. Материал передает ребенку сведения не только о числах и действиях с ними, но также дает ясное представление о единице – как о точке, о десятке – как о линии, о сотне – как о квадрате (площади) и о тысяче – как о кубе (теле, т. е. десятке возведенной в третью степень). Работая с «Золотым жемчужным материалом», ребенок открывает для себя тождественность десяти единиц разряда и единицы непосредственно следующего за ним разряда, важную роль числа десять в десятичной системе счисления, правила выполнения арифметических действий [2, 3, 7, 8].

Любое натуральное число может быть представлено посредством «Золотого жемчужного материала». Отдельные бусинки («жемчужины») заменяют единицы, палочки из десяти «жемчужин» – единицы десятков, квадраты из 100 «жемчужин» – единицы сотен и кубы из 1000 «жемчужин» – единицы тысяч («Карточки с единицами разрядов», рис. 2), а суммирование заменяется механическим объединением [2, 3, 7, 8].

Рисунок 2 – Карточки с единицами разрядов.

Рассмотрим пример на сложение многозначных чисел без перехода через разряд. Выполняется сложение с помощью «Золотого жемчужного материала» и карточек с единицами разрядов. Ученик получает набор карт из материала «Карточки с единицами разрядов» и составляет заданные многозначные числа. Затем берёт соответствующее множество бусин из «Золотого жемчужного материала». В ходе выполнения данного задания педагог спрашивает, сколько он принёс бусин, ученик берёт каждое множество, считает вслух и распределяет по разрядам. Одновременное использование вещественной («Золотой жемчужный материал») и знаковой («Карточки с единицами разрядов») учебных моделей обеспечивает оптимальность формирования умственных действий. В форме материализации обеспечивается практическое выполнение операций (руками), что играет важную роль в обучении детей. Проделывая большое количество подобных упражнений, ребёнок постепенно переходит к тому, что начинает «предвидеть» результаты своей работы без замены раскладки «Золотого жемчужного материала», и тем самым укорачивает механический процесс.

Рассматриваемый пример иллюстрирует глубину методической проработки материалов М. Монтессори, показывает один из аспектов разрешения проблемы формализма приобретения математических знаний в рамках её педагогики [2, 3, 7, 8].

В связи с этим, на базе ГБОУ РМ «Саранская общеобразовательная школа для детей с ограниченными возможностями здоровья» г. о. Саранск с учащимися четвертого класса нами был организован и проведён обучающий эксперимент, целью которого явилось формирование представлений о нумерации чисел в пределах 1000, их последовательности, отношениях и месте в натуральном ряду; представлений о десятичной системе счисления, умений выполнять арифметические действия сложения и вычитания.

Экспериментальное обучение началось со знакомства детей с «Золотым жемчужным материалом». Занятия проводились индивидуально с каждым учеником 4 класса. Обучение проводилось поэтапно: 1 этап: введение понятий количеств (единица, десяток, сотня, тысяча); 2 этап: обучение записи чисел: 1, 10, 100, 1000 (на карточках); 3 этап: построение десятичной системы счисления; 4 этап: арифметические действия (сложение и вычитание без перехода через разряд).

Охарактеризуем работу с материалом на каждом этапе. На первом этапе ученика знакомили с количествами, представляющими разряды десятичной системы счисления, в процессе чего ребёнок обнаруживал, что единицы каждого разряда состоят из десяти единиц предыдущего разряда. Знакомство проводилось в ходе трёхступенчатого урока.

Первая ступень: Педагог кладёт перед ребёнком бусину – единицу, спрашивает, сколько здесь бусин. Ученик отвечает: «Одна». Педагог говорит: «Одна единица». Ученик ощупывает бусину. Затем педагог кладёт перед ним стержень – десяток. Спрашивает сколько бусин – единиц на стержне и т. д. Аналогично ученик устанавливает, что десять десятков составляют одну сотню, десять сотен – одну тысячу.

Вторая ступень: Педагог даёт ученику задание: «Покажи одну единицу, тысячу и т. д.». Ученик при этом ощупывает, взвешивает, перекладывает каждый из этих предметов.

Третья ступень: ребёнок сам называет указанные учителем количества.

На втором этапе знакомили детей с числами 1, 10, 100, 1000 также в ходе трёхступенчатого урока.

Первая ступень: Учитель даёт ребёнку карту с числом 1, спрашивает, какое это число. После ответа ребёнка он констатирует: «Один или одна единица». Затем он даёт ребёнку карту с числом 10 и спрашивает, какое это число. Ребёнок: «Десять». Педагог: «Десять единиц». Числа 1 и 10 уже знакомы детям. Затем педагог показывает карточку с числом 100. Спрашивает сколько нулей в этом числе. Ученик: «Два». Учитель: «Это одна сотня». Аналогично вводится понятие 1000.

Вторая ступень: Педагог даёт ребёнку задание типа: «Дай мне одну сотню, покажи тысячу, возьми один десяток» и т. д.

Третья ступень: Учитель просит ученика назвать указанные им числа.

Далее с детьми проводились упражнения по раскладке большого набора карт 1–1000 из материала «Карточки с единицами разрядов».

1. Учитель раскладывает карты на ковре в правильном порядке. В правом верхнем углу находится карта 1, под ней все карты с числами 2–10. Левее раскладываются сначала десятки, потом сотни, потом тысячи, Нужно обратить внимание на то, чтобы между картами оставалось промежуточное пространство. Отдельные карты должны выниматься так легко, чтобы не нарушить порядок остальных карт. Порядок карт ребенок знает по «Золотому материалу» из бусин. То есть, учитель берёт карты 1–9 и начинает раскладывать их одну подругой сверху вниз. При этом называет числа: «Одна единица, две единицы», а затем ребёнок продолжает работу.

2. Карты с числами одного разряда перемешивают и кладут их снова одну под другую в эту же вертикальную колонку. При этом порядок карт в колонке меняется. Начинают с карт 10–90. Учитель просит ребёнка показать названные им единицы одного и того же разряда. Аналогично поступают с разрядами сотен и тысяч. Ребёнка просят также показать числа разных разрядов, например, 20, 400, 7000 и т. д.

3. Учитель просит ребёнка назвать указанные им числа. Карты убирают так, чтобы они хранились в правильном порядке.

На третьем этапе знакомили детей с построением десятичной системы счисления, с тем, что каждый разряд содержит не более девяти единиц; сопоставление количеств и соответствующих им чисел; учили узнавать названия разрядов десятичной системы, связывать названия разрядов с определенными геометрическими фигурами, узнавать структуру десятичной системы счисления.

Для введения понятия построения десятичной системы брали поднос с 10 отдельными бусинами, 10 стержнями по 10 бусин 10 квадратами по 100 бусин, одним кубом по 1000 бусин. Введение осуществляли лишь в том случае, если ребенок уже знает множества из 10 предметов и умеет считать до 10. Учитель с ребенком приносит поднос на стол. Педагог берет одну отдельную бусину, стержень из 10 бусин, квадрат из 100 бусин и куб из 1000 бусин и кладет их перед ребенком. После чего говорит: «Одна единица, две единицы, ... Ученик продолжает. Он строит ряд из девяти бусин – единиц. Слева от единиц стержни – десятки и считает вслух: «Один десяток, два десятка, ...» Левее девять квадратов – сотен и куб – тысяча. Затем учитель говорит: «Дай мне три единицы, дай девять десятков». Педагог обращает внимание ученика на то, что ряд пуст (см. рис. 3).

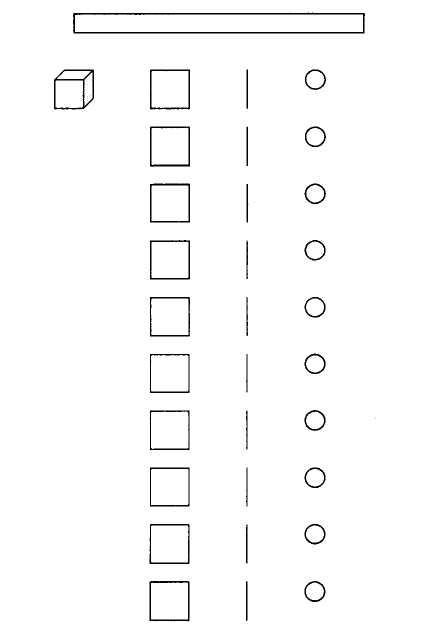
Рисунок 3 – Раскладка бусин.

Затем работают с набором карт 1–1000. Ребёнок самостоятельно раскладывает карты тем же образом, как и в случае с большим набором карт 1–9000. После этого педагог показывает ребенку связь между количествами и числами. На одной части раскладывают «Золотой материал», а на другой – большой набор карт 1–1000. Педагог даёт ребёнку карту и просит принести столько бусин, сколько указывает число на карте. По выполнении задания бусины пересчитывают. Педагог ребёнку поочерёдно предлагает карты с числами разных разрядов.

Для закрепления изученного проводят игру. Ребёнку дают некоторое количество «Золотого жемчужного материала» и просят принести соответствующие карты. По выполнении задания бусины пересчитывают и сопоставляют с числами на картах. Учитель предлагает ребенку из представленного набора предметов из бусин (отдельных бусин, стержней, квадратов, куба) выбрать определенные множества; учитель указывает на множество, ребенок должен его назвать и заменить следующим разрядом. Учитель дает ребенку большое множество бусин одного разряда, например, 20 отдельных бусин. Ребенок отсчитывает по 10 бусин, и каждый раз заменяет их десятком. Он должен по возможности самостоятельно найти способ решения задачи. Далее работают с картами. Учитель кладет карту с числом на пустой поднос и предлагает ребенку принести соответствующее множество бусин. Сначала берется только одна карта, позже – несколько карт с числами разных категорий, например, однозначным и двузначным, двузначным и трехзначным. Учитель и ребенок вместе проверяют, соответствует ли принесенное множество заданному числу. Затем выполняется обратное задание – ребенок получает множество из бусин и приносит соответствующие карты с числами. В заключении все действия ребенок выполняет самостоятельно.

На четвертом этапе знакомили детей с процессом сложения и вычитания без перехода через разряд. Ребенку предлагается пример: 2327 + 1242 = ... Числа 2327 и 1242, «записанные» с помощью карточек, и соответствующее им количество «жемчужин» выкладываются следующим образом: единицы разрядов второго слагаемого под соответствующими единицами разрядов первого. Выполняют сложение, объединяя и пересчитывая единицы поразрядно, а затем составляют полученное число (сумму) из карточек (рис. 4).

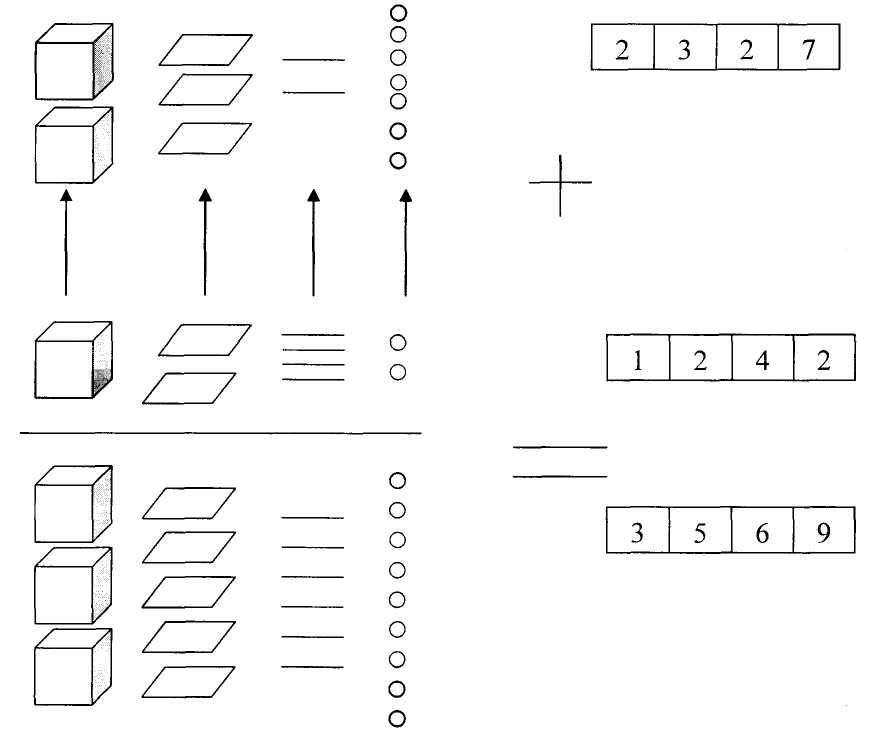
Рисунок 4 – Выполнение действия сложения.

Таким образом, работая с материалом, ребенок самостоятельно «открывает» правило сложения многозначных чисел столбиком («поразрядность» сложения). Одновременное использование предметной («Золотой жемчужный материал») и знаковой (карточки с единицами разрядов) учебных моделей обеспечивает оптимальность формирования умственных действий. Длительная работа с конкретными материалами позволяет детям глубоко понять смысл выполнения операции сложения многозначных чисел и не только без перехода, но и с переходом через десяток.

Проделывая большое количество подобных упражнений, ребенок постепенно переходит к тому, что начинает «предвидеть» результаты своей работы без замены и раскладки «Золотого жемчужного материала», и тем самым укорачивает механический процесс. Когда он воочию «увидит» в чем дело, то сможет выполнять более трудные действия при любом количестве цифр, общепринятым способом – «в уме»; будет владеть механизмом этих действий. В действительности здесь имеет место процесс интериоризации. Предвидение результатов работы означает выполнение некоторых промежуточных действий «в уме», а значит, переход их во внутренний план [2, 3, 7, 8].

В конце учебного года был проведён сравнительный контрольный эксперимент с целью выявления степени усвоения четвероклассниками с нарушением интеллекта предлагаемого материала, а также развивающего эффекта обучения с использованием элементов Монтессори-педагогики. Необходимо было выяснить, в какой степени предложенная методика повлияла на уровень сформированности вычислительных навыков учащихся с нарушением интеллекта в пределах 1000. С этой целью нами были обследованы дети экспериментальной и контрольной групп (контрольную группу составили учащиеся параллельного четвертого класса). Данные исследования свидетельствуют о весьма значительных различиях в выполнении заданий в пользу учащихся экспериментальной группы, существенными являются как качественные, так и количественные различия. Дети экспериментальной группы свободнее ориентировались в условии задания и успешнее выполняли счетные операции, их вычислительные навыки характеризовались правильностью, осознанностью, рациональностью, обобщенностью и прочностью.

Таким образом, эффективность предложенной нами методики, разработанной на основе методических подходов педагогической системы М. Монтессори, доказывают полученные результаты.

Литература

1. Аргинская, И. И. Математика. Методическое пособие к учебнику 2-го класса четырехлетней начальной школы / И. И. Аргинская. – М. : Центр общего развития, 2003. – 108 с.

2. Архипова, С. В. Пути совершенствования методики обучения математике детей с проблемами в развитии / С. В. Архипова, Г. В. Брыжинская, Л. Н. Гаврилова // Современные проблемы науки и образования. – 2015. – № 2 ; URL: http://www.science-education.ru/129-22274

3. Архипова, С. В. Формирование вычислительных навыков у учащихся младших классов с нарушением интеллекта / С. В. Архипова, Г. В. Брыжинская, Л. Н. Гаврилова // Современные наукоемкие технологии. – 2016. – № 5 (3); С. 504–508. URL: http://www.top-technologies.ru/ru/article/view?id=35942

4. Бантова, М. А. Система формирования вычислительных навыков / М. А. Бантова // Начальная школа. – 1993. – № 11. – С. 38–43.

5. Бантова, М. А. Методика преподавания математики в начальных классах : учеб. пособие для учащихся школьных отделений пед. училищ / М. А. Бантова, Г. В. Бельтюкова / под ред. М. А. Бантовой. – М. : Просвещение, 1984. – 335 с.

6. Белошистая, А. В. Методика обучения математике в начальной школе : курс лекций : учеб. пособ. для студ. вузов / А. В. Белошистая. – М. : Академия, 2011. – 455 с.

7. Брыжинская Г. В. Использование идей М. Монтессори в специальном дошкольном образовании // Дошкольное образование в стране и мире: исторический опыт, состояние и перспективы : материалы II международной научно-практической конференции 10–11 ноября 2013 года. – Прага : Vědecko vydavatelské centrum «Sociosféra-CZ», 2013 – С. 106–108.

8. Брыжинская Г. В. Реализация педагогического наследия М. Монтессори в инклюзивном образовании детей с ограниченными возможностями здоровья // Социосфера. – № 4. – 2013. – Том. 2. – С.75–77.