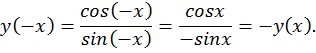Функция y = ctg x

Дата: 03.04.2020.

Тема: ФУНКЦИЯ y = ctg x

Цели: рассмотреть свойства функции котангенс и построить её график; закрепить новые знания в ходе решения задач.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Вспомните самостоятельно теорию, которая была изучена нами на прошлых уроках для функций y=sin x, у=соs x и y = tg x. Ответьте устно на вопросы.

1. Что называется областью определения функции? Каковы они для изученных функций?

2. Что называется множеством значений функции? Каковы они для изученных функций?

3. Как называются графики изученных ранее функций?

4. Что называется котангенсом угла α?

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Откройте свои тетради и запишите сегодняшнее число и тему урока. Далее выполняем построение графика функции у=ctg x и переписываем её свойства.

Давайте подумаем, как построить график функции у=ctg x? Вспомним формулу взаимосвязи

Т.е. график функции у=ctg x можно получить из графика функции y = tg x с помощью применения элементарных преобразований. Вспомним график функции y = tg x. К нему необходимо применить такие преобразования: смещение графика по оси Ох и отображение его симметрично относительно оси ОХ.

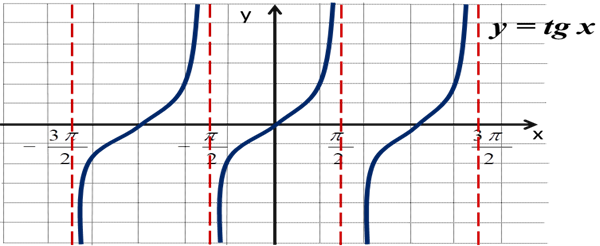
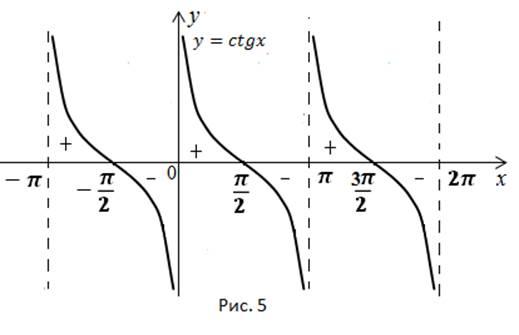
Применив эти преобразования, получим график для функции у=ctg x

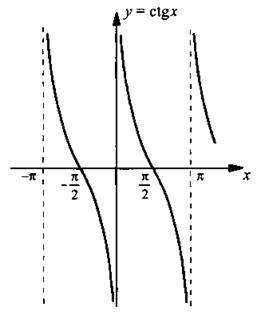
Перечислим основные свойства функции у = ctg x:

1. Область определения - множество всех действительных чисел, за исключением чисел вида х = πk, к ∈ Z.

2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.

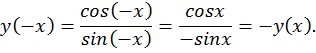
3. Функция убывает на промежутках вида (πk; π + πk), к ∈ Z.

4. Функция не ограничена.

5. Функция не имеет наименьшего и наибольшего значений.

6. Функция непрерывная.

7. Область значений Е(у) = (-∞; +∞).

8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + πk) = у(x).

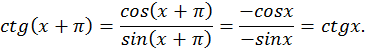
9. График функции имеет вертикальные асимптоты х = πk.

10. Точки пе­ре­се­че­ния с осью Оx: 

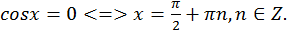
Точки пе­ре­се­че­ния с осью Оy от­сут­ству­ют.

11. Опре­де­лим ин­тер­ва­лы зна­ко­по­сто­ян­ства:

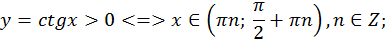
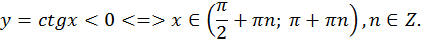
1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Пользуясь свойствами функции y = сtg x, выполните письменно №10.28, №10.31.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Какие свойства функции y = сtg x запомнили?

Домашнее задание: теория, №10.32.