Геометрические построения

Геометрические построения

Черчение 8 класс

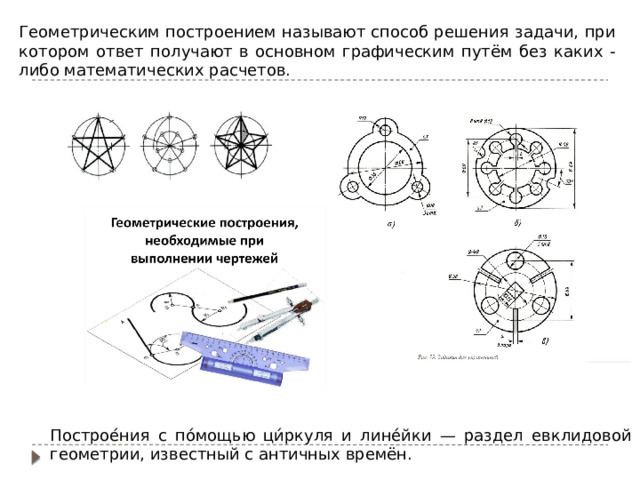
Геометрическим построением называют способ решения задачи, при котором ответ получают в основном графическим путём без каких - либо математических расчетов.

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.

Задание 4.

Деление отрезка прямой на равные части

Деление угла на две равные части

Деление прямого угла АВС на две равные части выполняется в следующей последовательности:

1. Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;

2. Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения в точке К;

3. Точку К соединяют с вершиной В прямой, которая разделяет угол АВС на две равные части.

Задание 5.

Деление окружности на три, шесть и двенадцать равных частей

Деление окружности на три, шесть и двенадцать равных частей выполняется в следующей последовательности:

1. Выбираем в качестве точки 1, точку пересечения осевой линии с окружностью;

2. Из точки 4 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 2 и 3;

3. Точки 1, 2 и 3 делят окружность на три равные части;

4. Из точки 1 пересечения осевой линии с окружностью проводим дугу радиусом равным радиусу окружности R до пересечения с окружностью в точках 5 и 6;

5. Точки 1 - 6 делят окружность на шесть равных частей;

6. Дуги радиусом R, проведенные из точек 7 и 8 пересекут окружность в точках 9, 10, 11 и 12;

7. Точки 1 - 12 делят окружность на двенадцать равных частей.

Деление окружности на пять равных частей выполняется в следующей последовательности:

1. Из точки А радиусом, равным радиусу окружности R, проводим дугу, которая пересечет окружность в точке В;

2. Из точки В опускают перпендикуляр на горизонтальную осевую линию;

3. Из основания перпендикуляра - точки С, радиусом равным С1, проводят дугу окружности, которая пересечет горизонтальную осевую линию в точке D;

4. Из точки 1 радиусом равным D1, проводят дугу до пересечения с окружностью в точке 2, дуга 12 равна 1/5 длины окружности;

5. Точки 3, 4 и 5 находят откладывая циркулем по данной окружности хорды, равные D1.

Деление окружности на пять равных частей

Задание 6.

Постройте звезду по алгоритму