Муниципальное бюджетное общеобразовательное учреждение
"Центр образования № 22 - Лицей искусств"
Научно-исследовательская работа
по предмету
Геометрия
На тему: «Геометрия пчелиных сот»
Выполнил: Ученица 11А класса Симонова Мария Николаевна
Научный руководитель:
Сватковская Елена Александровна
Тула 2023
Содержание
Введение ………………………………………………………………3
Глава 1. Пчёлы – инженеры……...……………………………..…..…5
1.1 Пчёлы, какие они?......................................................................
1.2 Процесс создания сот…………………………………………
Глава 2. Гипотеза может быть доказана ………………………………
2.1 Почему пчелы предпочли сеть правильных шестиугольников при построении сот?..................................................................................
2.1.1 Какими правильными многоугольниками можно заполнить плоскость в виде паркета?................................................................
2.1.2 Почему именно правильный шестиугольник имеет наименьший периметр?..................................................................................................
2.2 Почему дно сотовых ячеек представляет собой трехгранные углы, в качестве граней которых служат ромбы?.................................................
2.2.1 Доказательство того, что объем ячейки равен объему правильной шестиугольной призмы…………………………………………………….
2.2.2 Что имеет меньшую площадь поверхности: ячейка или правильная шестиугольная призма?................................................................
Сколько экономят пчелы?...............................................................
2.3 Построение сотовой ячейки, ее развертки и ее проекций………..
Глава 3. Применение конструкции пчелиных сот …………………………….
3.1 Сотовые панели…………………………………………………….
3.2 Газонная решётка …………………………………………………….
3.3 Архитектура сети сотовой связи……………………………………..
Заключение……………………………………………………………………….
Список источников и литературы……………………………………………..
Введение
Актуальность работы: Весь процесс строения сот очень удивительный, наблюдая за самим процессом создания, можно заметить много, что можно изучить глубже, и как это будет отражено в жизни. Многие люди не задумываются о том, почему пчёлы выбирают именно такую фигуру, для этого нам понадобятся знания школьного курса геометрии, мы научимся применять их в жизни. Это поспособствует расширению кругозора и уделение более пристального внимания школьному материалу.
Цель работы. Изучить жизнь пчелиной семьи с целью решения задач практического характера с применением приобретенных знаний в школе, а так же показать эффективность математики и её связь с жизнью.
Задачи:
Используя литературные источники, найти, выбрать, проанализировать нужную информацию;
Исследовать строение пчелиных сот на экономичность, вместимость, практичность, выполнив математические расчёты;
Доказать совершенство конструкции пчелиных сот;
Гипотеза: Форма шестиугольной призмы самая оптимальная для экономичного использования и постройки сот.
Объект: Математическая модель сот.
Предмет: Пчела и её соты.
Методы исследования: математический анализ, моделирование, сравнительный анализ.
Практическая значимость проекта: Показывает точность построения сот пчёлами, а так же использование геометрических закономерностей построения в жизни человека.
Глава 1.Пчелы – инженеры.
1.1 Пчелы, какие они?
На протяжении сотен лет внимание людей не только привлекала необычная архитектура пчелиных сот, но и удивляла красота и правильность их построения. Это настоящий математический шедевр из воска, созданный очень кропотливым трудом умных пчёл.

Пчели́ные со́ты — восковые постройки медоносных и близких к ним видов пчёл (большой, карликовой и средней индийских), состоящие из упорядоченных ячеек. Соты служат вместилищем для яиц, личинок и пищевых запасов (мёда и перги), а также местом пребывания для взрослых насекомых. Соты состоят из шестиугольных ячеек, расположенных по обе стороны от общего средостения, которое может быть искусственным.
Допуск на стройплощадку в улье не получает ни молодёжь, ни пенсионеры. Средний возраст пчелиного "стройбата": 12-18 дней, так как в этот период начинают действовать восковые железы, и пчела начинает вместе с другими особями заделывать ячейки и строить соты.
Среди многих инстинктивных проявлений, свойственных пчелам как общественным насекомым, наибольшее восхищение вызывает создание ими идеальных по форме сот. Восковые ячейки с золотым сладким нектаром – не что иное, как произведение искусства в инженерии. В основе конструкции шестиугольник правильной формы, окруженный множеством ячеек той же формы.
Пчелы скоординировано, быстро и умело строят в улье вертикальные ряды ячеек из воска, выделяемого брюшными железами.
Живший в Древней Греции философ Папп Александрийский полагал, что у пчел есть уникальная способность – геометрическое предвидение. И был уверен, что такими знаниями насекомых мог наделить только Господь. Существовало и множество других теорий, которые были основаны на домыслах и рассуждениях. Чарлз Дарвин не был уверен ни в одной из них, и отвергал их реалистичность. Он долгое время проводил эксперименты в попытках выяснить, смогут ли медоносные насекомые построить восковые ячейки идеальной формы, руководствуясь лишь врожденными и приобретенными навыками, о чем гласит теория эволюции. Дарвина все равно мучил один и тот же вопрос – почему соты шестиугольные? Оказалось, это имеет довольно простое объяснение. Если вы попробуете заполнить любую плоскость так, чтобы не осталось пустых мест, подходящими будут всего три геометрические фигуры, стороны и углы у которых равны, а именно: треугольники, квадраты и шестиугольник правильной формы.
Объяснить такие «познания» пчел ученым пока не удалось. Ведь эти насекомые не знают геометрии, не могут сравнивать между собой разные формы сосудов, чтобы выбрать наиболее оптимальную форму. Значит, пчелы были изначально обеспечены уникальной врожденной программой и инстинктом, которые позволили им выживать в течении миллионов лет.
1.2 Процесс создания пчелиных сот.
В качестве основных материалов для формирования соты пчел используются цветочный прополис и воск. Подобные ячейки выполняют сразу три жизненно важных функции: выращивание личинок, а также размещение пчелиного семейства и хранение собранного меда.
Толщина соты 25 мм. Пласты прикрепляются вертикально на расстоянии 10-12 мм. Это расстояние называется улочкой и пчёлы, сидя на соседних сотах, не касаются друг друга спинками.
Ячейки сот формируются над старыми, заполняются вкусным лакомством, а сверху запечатываются еще одним слоем воска. Над этими ячейками появляются еще одни, и так продолжается весь сезон.
Сооружение ячеек происходит таким образом. Пчела выделяет воск, передними лапками подводит его к челюстям и перерабатывает. Чешуйки воска раздавливаются при помощи особого пчелиного вещества, а их фрагменты один за другим крепятся в нужное место. Сначала насекомые формируют дно, а затем возводят стенки шестиугольной формы.
И что удивительно, то весь процесс построения сот происходит в полной темноте. Пчела не может использовать органы зрения, т.к. в темноте она не видит. Для построения сот одной семье требуется 4-6 кг воска. Других материалов пчёлы при строительстве не применяют. На выделение 1 кг воска расходуется 3 кг мёда. За год одна пчелиная семья поедает 70 – 90 кг мёда, из них 10-12 кг мёда расходуется в период зимовки.
Глава 2. Гипотеза может быть доказана
2.1 Почему пчелы предпочли сеть правильных шестиугольников при построении сот?
Если разрезать пчелиные соты плоскостью, перпендикулярной их ребрам, то станет видна сеть равных друг другу правильных шестиугольников, уложенных в виде паркета.
Возникает вопрос: Почему пчелы строят соты именно так, почему они выбрали сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь кажется, что гораздо проще сконструировать?
1) Чтобы ответить на этот вопрос, надо предварительно выяснить, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пустот, т.е. уложить их в виде паркета.
Выполняя такие расчеты, убеждаемся, что такими многоугольниками могут быть только правильные треугольники, квадраты или шестиугольники.
И ведь действительно, сумма внутренних углов выпуклого n-угольника равна
 , где n-число сторон многоугольника.
, где n-число сторон многоугольника.
Сумма углов правильных n-угольников, сходящихся в одной вершине
паркета, равна 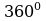 .
.
Тогда  , где
, где  -число углов, сходящихся в одной вершине паркета. Т.е.
-число углов, сходящихся в одной вершине паркета. Т.е.  .
.
| n | k | Количество многоугольников |
| 3 | 6 | в одной вершине паркета могут сходиться 6 правильных треугольников |
| 4 | 4 | в одной вершине паркета могут сходиться 4 квадрата |
| 5 | 3,3 | не существует паркета из правильных пятиугольников |
| 6 | 3 | в одной вершине паркета могут сходиться 3 правильных шестиугольника |
| 7 | 2,8 | не существует паркета из правильных семиугольников |
| и так далее |
|
|
Теперь рассуждаем следующим образом.
 , т.к. внутренний угол правильного многоугольника меньше
, т.к. внутренний угол правильного многоугольника меньше  ;
;
Значит,  , или
, или  .
.
По смыслу задачи значения n, k и  могут быть только целыми, поэтому n=3, 4, 6.
могут быть только целыми, поэтому n=3, 4, 6.
Мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, или квадраты, или правильные шестиугольники.
2) Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не квадрат или правильный треугольник, рассмотрим вспомогательную задачу №1 :
Даны три равновеликие друг другу фигуры – правильный треугольник, квадрат и правильный шестиугольник. Какая их данных фигур имеет наименьший периметр?
Пусть  ,
,
 -стороны соответствующих правильных n-угольников.
-стороны соответствующих правильных n-угольников.
| Площадь n-угольника | Сторона n-угольника | Периметр n-угольника |
| 
| 
| 
|
| 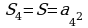
| 
| 
|
| 
| 
| 
|
Для сравнения периметров фигур найдем их отношение

Мы видим, что из трех правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, мудрые пчелы экономят воск и время для построения сот.
2.2 Почему дно сотовых ячеек представляет собой трехгранные углы, в качестве граней которых служат ромбы?
Еще один интересный вопрос, почему пчелы строят донышки своих ячеек в форме трехгранного угла, в качестве граней которого служат ромбы.
Неужели нельзя было сделать проще, дно сот плоским, т.е. обычным правильным шестиугольником? Какая здесь выгода для пчел?
А) Вернемся к ячейке – многограннику на рисунке 1.
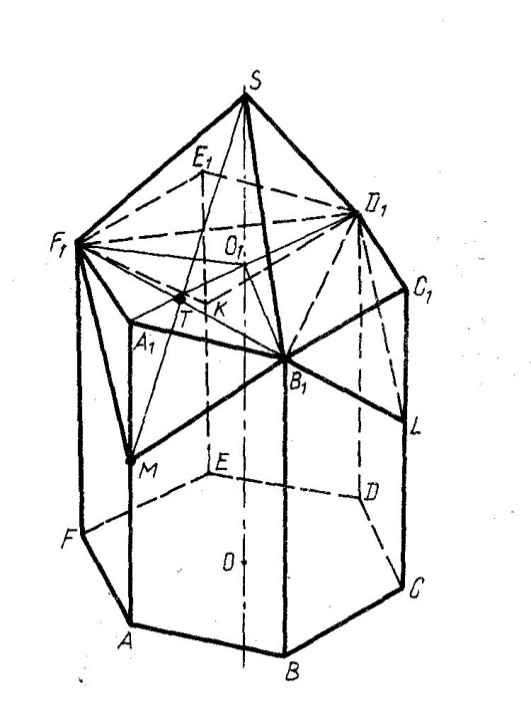
Рисунок 1
Объем многогранника
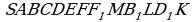 равен объему правильной шестиугольной призмы
равен объему правильной шестиугольной призмы
 . Как нетрудно заметить, объем пирамиды
. Как нетрудно заметить, объем пирамиды  равен утроенному объему одной из равных пирамид
равен утроенному объему одной из равных пирамид  . Пирамиды
. Пирамиды  и
и  равны (они симметричны относительно точки Т).
равны (они симметричны относительно точки Т).
Итак, объемы пчелиной ячейки и правильной шестиугольной призмы  равны.
равны.
Б) В задаче 1 из равновеликих многоугольников выбирали тот, который имеет наименьший периметр. Попробуем теперь решить задачу:
Из данных равновеликих многогранников (правильная шестиугольная призма и «пчелиная ячейка») найти тот, у которого наименьшая площадь поверхности.
Как нетрудно видеть из рисунка 3, каждому положению точки S на оси ОО соответствует свой многогранник
соответствует свой многогранник 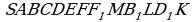 .
.
Пусть АВ=а, ВВ =b и SO
=b и SO =x, причем
=x, причем  . Определим то значение
. Определим то значение
переменной x, при котором площадь поверхности многогранника-
ячейки наименьшая.
Введем функцию S (x) площади поверхности многогранника – ячейки
(x) площади поверхности многогранника – ячейки
(без нижнего основания). Воспользуемся снова рисунком 3.
Найдем  .
.
Рассмотрим равнобедренный треугольник  :
:  ,
,
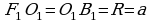 ,
,  .
.
 .
.
Площадь ромба равна половине произведения его диагоналей:
 ,
,
 ,
,  ,
,

 ,
,
 .
.
Площадь полной поверхности состоит из шести равных трапеций и
трех равных ромбов, т.е.


Для ответа на вопрос задачи о наименьшей площади поверхности надо
найти минимум функции S , заданной на множестве положительных
, заданной на множестве положительных
чисел.
Найдем критические точки функции S :
:
 ,
,

Легко проверить, что при  производная
производная  .
.
Функция S непрерывна на всей области определения, других
непрерывна на всей области определения, других
минимумов на интервале  не имеет, поэтому в точке
не имеет, поэтому в точке 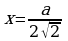
она принимает свое наименьшее значение и 
 .
.
Найдем площадь поверхности правильной шестиугольной призмы без
нижнего основания :
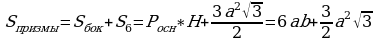 .
.
 .
.
А площадь поверхности ячейки равна  , ее объем
, ее объем
равен объему той же шестиугольной призмы, т.е. 
 .
.
В) Найдем, сколько же сэкономили пчелы на постройке всего лишь
одной ячейки сот:
Для этого найдем разность площадей
 .
.
Как видим, пчелиная ячейка имеет такой же объем, как и правильная шестиугольная призма, а так как площадь ее поверхности меньше площади поверхности призмы, то стоит только удивляться экономности пчел.
В имеющейся литературе приводятся сведения о том, что благодаря такой «математической» работе расчетливые «геометры» экономя около 2% воска. Количество воска, сэкономленного при постройке 54 ячеек, может быть использовано для одной такой же.
В итоге необходимо сказать, что пчелиные соты представляют собой
пространственный паркет, поскольку заполняют пространство так, что
не остается просветов.
Построение сотовой ячейки, ее развертки и ее проекций.
Но на этом математические секреты пчел не заканчиваются. Дальше еще интереснее исследовать строение пчелиных сот.
Соты в улье свешиваются сверху вниз наподобие занавесок: пчелы прикрепляют их к потолку смесью воска и пчелиного клея (прополиса). Ячейки уложены в пласты и соприкасаются общими донышками. Но донышки ячеек не плоские, а представляют собой части трехгранных углов, гранями которых являются равные ромбы.
На рисунке 1 изображена пчелиная ячейка в общем виде, а на рисунке 2 –
е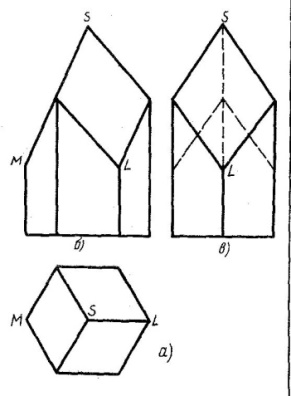
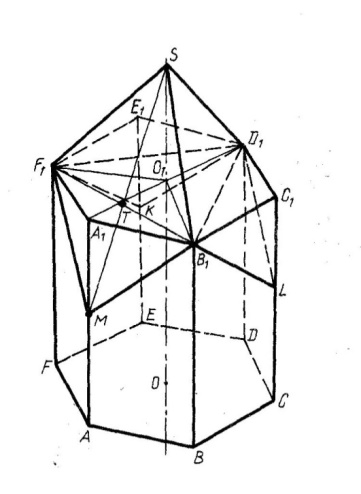
е проекция: вид сверху, вид спереди и вид сбоку.
Рисунок 1 Рисунок2
Попробуем построить развертку многогранника SABCDEFF MB
MB LD
LD K (одна ячейка сот). Но прежде чем начать построение развертки, необходимо рассмотреть чисто геометрически, как получается ячейка.
K (одна ячейка сот). Но прежде чем начать построение развертки, необходимо рассмотреть чисто геометрически, как получается ячейка.
Начнем с построения изображения правильной шестиугольной призмы  . Проведем диагонали
. Проведем диагонали  верхнего основания призмы и на оси призмы
верхнего основания призмы и на оси призмы  возьмем некоторую точку S (рисунок 1).
возьмем некоторую точку S (рисунок 1).
Через прямые  и точку S проводим три плоскости, которые отсекают от призмы три равные треугольные пирамиды
и точку S проводим три плоскости, которые отсекают от призмы три равные треугольные пирамиды 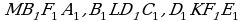 . Получившийся многогранник
. Получившийся многогранник 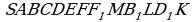 и является пчелиной ячейкой.
и является пчелиной ячейкой.
И так как боковая поверхность многогранника представляет собой шесть равных между собой трапеции, то для получения развертки построим эти трапеции. Их размеры возьмем такими же, как на рисунке 2, причем отрезок MS на рисунке 2а –это диагональ ромба в верхней части ячейки.
Р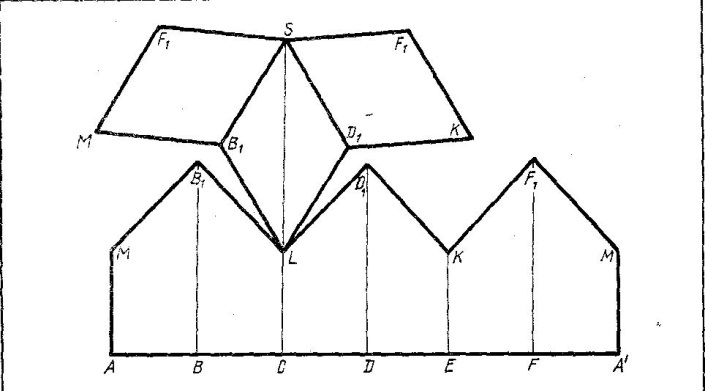
исунок 3
Построим отрезок  (рисунок 3).
(рисунок 3).
На продолжении ребра CL от точки L отложим отрезок LS и из точки L проведем окружность радиусом, равным, например, отрезку  . После этого построим середину отрезка LS, проведем через нее перпендикулярную к нему прямую, которая пересекает дугу окружности в двух вершинах ромба.
. После этого построим середину отрезка LS, проведем через нее перпендикулярную к нему прямую, которая пересекает дугу окружности в двух вершинах ромба.
Два других ромба строим следующим образом: из вершины ромба  проводим окружность радиусом, равным стороне построенного ромба, а из вершины S- окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба. Остальные построения очень просты.
проводим окружность радиусом, равным стороне построенного ромба, а из вершины S- окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба. Остальные построения очень просты.
Развертка пчелиной ячейки показана на рисунке 5. А на рисунке 4 можно увидеть, как соприкасаются ячейки в улье; их общая часть является ромбом.

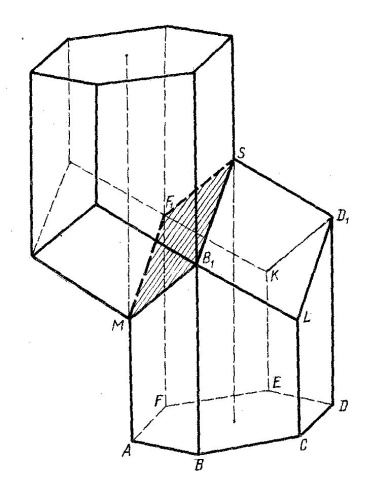
Рисунок 4 Рисунок 5
Когда говорят о пчелах, то чаще всего демонстрируют рисунок 6, показывающий соты в разрезе плоскостью, перпендикулярной боковому ребру и пересекающей все соты по правильным шестиугольникам. Если продолжить одну из боковых граней ячейки так, чтобы она пересекала остальные соты, то сечение будет таким, как показано на рисунке 7.
Р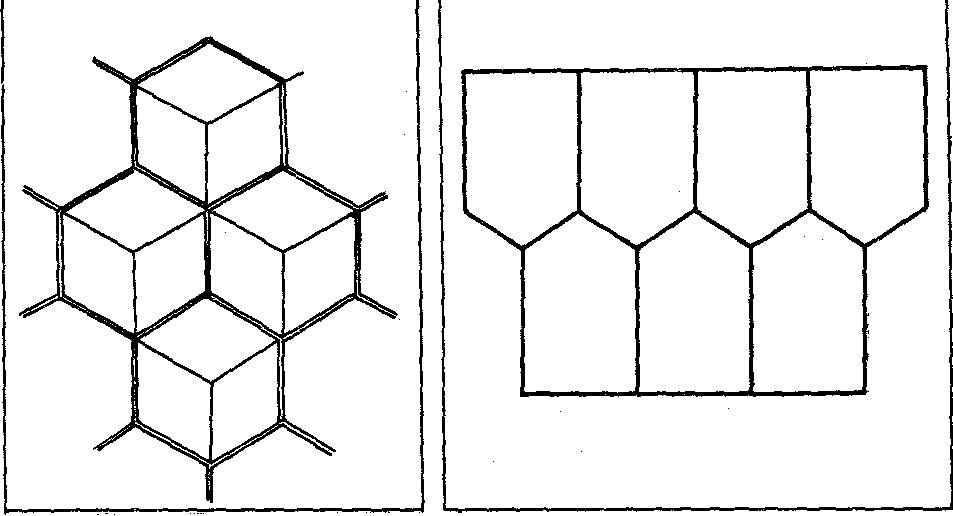
исунок 6 Рисунок 7
Глава 3. Применение конструкции пчелиных сот
3.1 Сотовые панели
Сотовые панели – это конструкция с внутренней алюминиевой прослойкой. Между двумя алюминиевыми листами находится наполнитель шестиугольной формы, который имеет «ячеистую» структуру. Сотовые панели широко используются в строительстве. В перспективе могут использоваться в конструкциях интерьера т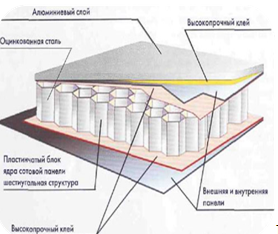 ранспортных средств.
ранспортных средств.
Рисунок 8- Сотовая панель
По конструкции сотовые панели представляют собой материалы, состоящие из тонкостенных пустотелых ячеек. Все ячейки имеют одинаковую шестигранную форму (аналогично пчелиным сотам). Сотовые панели применяют для изготовления силовых конструкциях, т.е. тех, которые несут нагрузку., а также в тепло- и звукоизолирующих конструкциях. Сотовые панели используют в судостроении, конструкциях летательных аппаратов вследствие низкой плотности), транспортных средствах (рефрижераторы), криогенной технике, строительстве и других целях. В летательных аппаратах получили распространение термостойкие и трудногорючие сотовые панели на основе термостойких бумаг из фенилона (номекса) и термостойких связующих. Такие сотовые панели обладают минимальной массой при достаточно высоких механических свойствах.
Сотовые конструкции также используются при изготовлении лопастей несущего винта вертолётов, что позволяет продлить срок их службы с 200 до 2000 часов, увеличить надёжность и аэродинамические характеристики. Одновременно снижается трудоёмкость их изготовления в 1.5-2 раза.
В настоящее время производство сотовых панелей развивается и в Росси и за рубежом. Основные поставщики сотовых панелей на Европейском рынке и в США являются компании CELCOMPONENTSS.r.l (Италия), PlascoreIncorporated (США), Pacific PanelsInc.(США), XENAPAN (Турция),
Panelium Kompozit Sistemleri (Турция), Tosolbond Composites( Индия). На российском рынке производством сотовых панелей занимаются такие компании как, ООО НПП "Технология" (г. Обнинск), ООО «Экосистем»
(г.Чехов, Московская область), ЗАО «Рекаст» (г. Сосенский, Калужская область).
3.2 Газонная решётка

Рисунок 9 - Газонная решётка
Газонные решетки - состоят из многофункциональной пространственной структуры модулей типа "пчелиные соты». Они придают травяному укрытию высокую устойчивость к механическим нагрузкам. Газонные решетки также предназначены для применения на автомобильных стоянках. Тонкие стенки их составных элементов выносят большие поверхностные нагрузки (как и прочные пчелиные соты).
3.3 Архитектура сети сотовой связи
Сначала надо понять из чего состоит сеть сотовой связи, то есть какие основные элементы она содержит.
Во-первых это центр сети или Core. Он может быть для голосовых или пакетных сообщений и служит для адресования входящих вызовов или пакетов к другим регионам страны или в сеть Интернет.
В сети GSM и UMTS (2G и 3G, соответственно) имеется контроллер базовых станций BSC - 2G, RNC - 3G. Его задачи состоят в управлении радиосетью, подстройки параметров отдельных базовых станций, налаживания взаимодействия между ними, а также обмена данными с Core. Сеть LTE лишена контроллера базовых станций, так как его функции заключены в функционал самой базовой станции.
Ну и на конец самый важный элемент - это базовые станции (БС), которые устанавливаются на башнях связи и разных домах внутри городов и деревень для обеспечения покрытия сотовой связи на заданной территории.
Ниже на схеме можно примерно представить себе архитектуру сети сотовой связи:
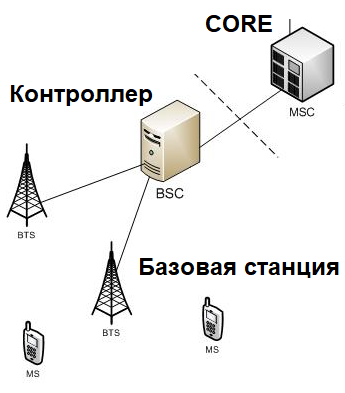
Почему сотовую связь называют сотовой.
Так вот именно из-за принципа размещения тех самых базовых станций сотовая сеть и получила своё название.
Дело в том, что начальный план размещения базовых станций на местности представляет собой сотовую структуру - очень похожую на пчелиные соты. И это неслучайно, так как стандартная базовая станция включает 3 сектора (панельные антенны), которые покрывают всё пространство вокруг одной станции. Наличие трёх антенн на БС также не случайно. Панельные антенны имеют стандартную ширину излучения или, говоря научно, диаграмму направленности. Она как раз позволяет создать покрытие мобильной сети в секторе примерно 120 градусов. Отсюда и получается нижеследующая картина:
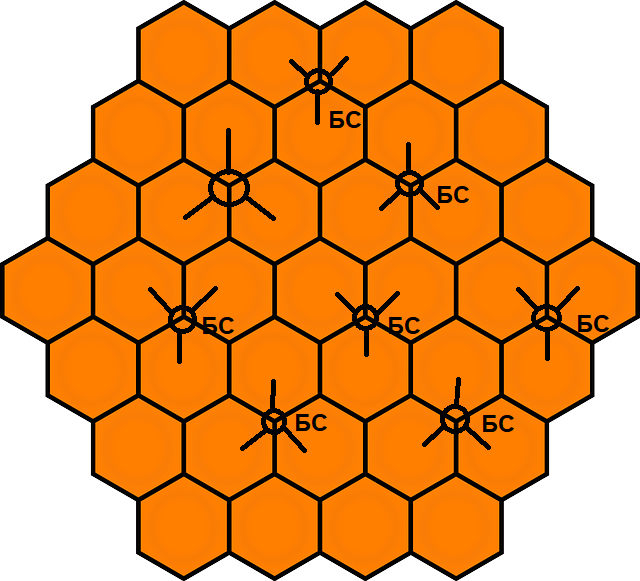
Сотовая структура размещения базовых станций (БС)
Конечно же на практике очень сложно найти подходящие объекты под размещение объектов сотовой связи, чтобы укладываться в сотовую структуру (как на рисунке выше). Поэтому в картах размещения базовых станций очень сложно найти улей, но тем не менее название это прижилось и сотовой связь называют по всему миру, а не только в России.
Заключение.
Такой опыт в работе дал мне возможность подробнее разобраться с таким понятием в геометрии , как призма. На мой взгляд, строительство пчелиных сот довольно интересный процесс, который можно связать с проектированием. Ведь разработка моделей это очень важно, нужно учитывать все нюансы, что и делают пчелы при строительстве своих сот. Шестиугольная призма это идеальная геометрическая форма для максимального использования единицы площади и минимальных затрат для ее постройки.
Считаю свою работу довольно полезной и содержательной. Думаю, что все задачи, поставленные для достижения цели, выполнены.
Список источников и литературы
Литература:
Погорелов А.В., Геометрия 7 – 10 кл
Детская энциклопедия: Что? Где? Почему?
Интернет ресурсы:
https://ru.m.wikipedia.org/wiki/Пчелиные_соты
http://pcheliniydom.ru/pchelovodstvo/paseka/kak-pchely-delayut-soty.html








 , где n-число сторон многоугольника.
, где n-число сторон многоугольника.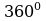 .
. , где
, где  -число углов, сходящихся в одной вершине паркета. Т.е.
-число углов, сходящихся в одной вершине паркета. Т.е.  .
.  , т.к. внутренний угол правильного многоугольника меньше
, т.к. внутренний угол правильного многоугольника меньше  ;
; , или
, или  .
. могут быть только целыми, поэтому n=3, 4, 6.
могут быть только целыми, поэтому n=3, 4, 6. ,
,  -стороны соответствующих правильных n-угольников.
-стороны соответствующих правильных n-угольников.


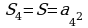







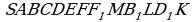 равен объему правильной шестиугольной призмы
равен объему правильной шестиугольной призмы  . Как нетрудно заметить, объем пирамиды
. Как нетрудно заметить, объем пирамиды  равен утроенному объему одной из равных пирамид
равен утроенному объему одной из равных пирамид  . Пирамиды
. Пирамиды  и
и  равны (они симметричны относительно точки Т).
равны (они симметричны относительно точки Т). соответствует свой многогранник
соответствует свой многогранник  . Определим то значение
. Определим то значение (x) площади поверхности многогранника – ячейки
(x) площади поверхности многогранника – ячейки  .
. :
:  ,
, 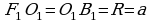 ,
,  .
. .
. ,
, ,
,  ,
,
 ,
, .
.

 , заданной на множестве положительных
, заданной на множестве положительных ,
,
 .
. не имеет, поэтому в точке
не имеет, поэтому в точке 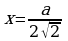

 .
. 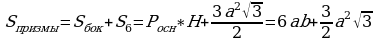 .
. .
. , ее объем
, ее объем
 .
. .
.

 верхнего основания призмы и на оси призмы
верхнего основания призмы и на оси призмы  возьмем некоторую точку S (рисунок 1).
возьмем некоторую точку S (рисунок 1).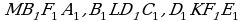 . Получившийся многогранник
. Получившийся многогранник 
 (рисунок 3).
(рисунок 3).  . После этого построим середину отрезка LS, проведем через нее перпендикулярную к нему прямую, которая пересекает дугу окружности в двух вершинах ромба.
. После этого построим середину отрезка LS, проведем через нее перпендикулярную к нему прямую, которая пересекает дугу окружности в двух вершинах ромба. проводим окружность радиусом, равным стороне построенного ромба, а из вершины S- окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба. Остальные построения очень просты.
проводим окружность радиусом, равным стороне построенного ромба, а из вершины S- окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба. Остальные построения очень просты.

 ранспортных средств.
ранспортных средств.












