Просмотр содержимого документа
«Геометрия Тема:Фалестин теоремасы.»
| Сабак 7 | Предмети: геометрия | 8-класс | 1-чейрек | Мугалим: __________ Текшерди:__________ |
| Сабактын темасы: | Фалестин теоремасы |
| Сабактынтиби: | Жаңы билимди өздөштүрүү |
| Колдонулуучу усулдар жана ыкмалар: | интерактивдуу.Өз алдынча иштөө, жупташып иштөө. Өзүн-өзү баало, калыптандыруучу, диагностикалык баалоо |
| Сабакта колдонулуучу каражаттар жана материалдар: | окуу китеби, сүрөттөр, проектор, интерактивдүү доска ж.б Султанбаев “Геометрия 8-кл” |
|
| Негизги копетенттүүлүктөр:(НК 1) ,(НК 2) ,(НК 3) Предметтик компетенттүүлүк 1.Маалыматтык компетенттүүлүк (НК 1) (ПК1) 2.Социалдык коммуникативдик комп (НК 2 (ПК2)(ПК3) 3. “Өзүн өзү уюштуруу жана көйгөйлөрдү чечүү”(НК3)(ПК4) |
| Сабактын максаттары: | Көрсөткүчтөр,Күтүлүүчү натыйжалар |
|
| Билим берүүчүлүк максаты: |
|
| Фалестин теоремасы жонундо тушунку алышат. Аныктамасын касиеттерин билет.Теореманы колдонуп мисалдарды иштегенди уйронушот | Мисалдарды чыгарууда касиеттерин колдонот. |
| Өнүктүрүүчүлүк максаты: |
|
| Мисалдарды чыгаруу аркылуу билим, билгичтиктерди бышыктайт.кондумдору калыптанат | Өз алдынча мисалдарды чыгаруу менен түшүндүрүп бере алат |
| Тарбиялоочулук максаты: |
|
| Тырышчаактыкка, жоопкерчиликке, кол көтөрүп сүйлөөгө тарбиялоо | Окуу куралдарын туура пайдаланууга тарбияланат |
Сабактын жүрүшү:
| Этап | убакыт | Мугалимдин иш аракети | Окуучунун иш аракети |
| Уюштуруу, | 3-мүн | | Сабакты жакшы кабыл алууга өбөлгө түзүлөт |
| 
|
| Өтүлгөн сабакты кайталап үй тапшырмаларын текшерүү жана окуучу түшүнбөй калган жерлерин кайра түшүндүрүрүп берүү | |
|
|
| Акыл гимнастикасы окуучуларга суроо: Ромб деп эмнеге айтылат? Ромбдун касиетин айт.
2) Квадрат деп эмнеге айтылат? Анын касиеттерин айт.
3) Квадратка: a) «параллелoграмм»; б) «ромб»; в) «тик бурчтук» түшүнүктөрү жардамында аныктама бер
| Аң сезими ойгонот Ойлонот Изденет Табат |
ФАЛЕСТИН ТЕОРЕМАСЫ
Теорема: Эгерде бурчтун жактарын кесүүчү параллель түз сызыктаранын бир жагынан барабар кесиндилерди бөлсө, алар экинчижагынан да барабар кесиндилерди бөлөт.
Далил. O бурчтун бир жагында (a шоолада) өз ара барабар A1A2 жана A2A3 кесиндилер коюлган жанa алардын акыры (A1, A2, A3) аркылууэкинчи жакты (b шооланы) B1, B2, B3 чекиттердекесүүчү өз ара параллель A1B1, A2B2 жана A3B3түз сызыктар жүргүзүлгөн болсун (1сүрөт). 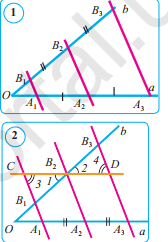
Эми алынган B1B2 жана B2B3 кесиндилердин өз ара барабардыгын, б.а. эгерде A1A2 =A2A3 болсо, анда B1B2 =B2B3 болушун далилдейбизАл үчүн B2 чекитинен a шоолага параллель
CD түз сызыгын жүргүзөбүз (2сүрөт). Бултүз сызык A1B1 жана A3B3 тиешелүү түрдө C
жанa D чекиттерде кесилишсин. A1CB2A2 жанаA2B2DA3 төрт бурчтуктар – параллелoграмм
(аныктама боюнча), анткени алардын карамакаршы жактары шарт жанa түзүлүшү боюнча параллель. Шарт боюнча,A1A2 =A2A3 жана параллелограммдын карамакаршы жактары болгондуктанA1A2= CB2 жана A2A3=B2D лардан CB2=B2D гa ээ болобуз..
B1B2C жана B3B2D үч бурчтуктарында CB2=B2D (далил боюнча), ошондуктан, ∠1= ∠2 (вертикалдуу бурчтар), ∠3= ∠4 (A1B1 жана A3B3 параллельтүз сызыктар жанa CD кесүүчүнүн кесилишинен алынган ички кайчылашбурчтар болгондуктан).
Үч бурчтуктар барабардыгынын экинчи белгиси боюнча, бул үч бурчтуктар өз ара барабар: ∠B1B2C= ∠B3B2D. Мындан B1B2=B2B3 келип чыгат.
Ошентип, эгерде A1A2=A2A3 болсо, анда B1B2=B2B3 болушу далилденди. Ушуну далилдөө талап кылынган эле.
Эскертме! Фалес теоремасынын шартында бурчтун ордуна ар кандай
эки түз сызыкты алууга болот, мында теореманын корутундусу өзгөрбөйт.
Натыйжа. Берилген эки түз сызыкты кесүүчү жанa түз сызыктардын биринен барабар кесиндилерди бөлүүчү параллель түз сызыктар экинчи түз сызыктан да барабар кесиндилерди бөлөт.
. ФАЛЕСТИН ТЕОРЕМАСЫ ЖАНA АНЫН КОЛДОНУЛУШУ
1маселе. (Кесиндини барабар бөлүктөргө бөлүү.) Берилген ABкесиндини n барабар бөлүккө бөл.
Чыгаруу. AB кесинди берилген болсун. Аны n барабар бөлүккөбөлүүнү көрсөтөбүз. A чекитинен AB түз сызыкта жатпаган AC шооланыжүргүзөбүз жанa анда A чекитинен баштап n AA1, A1A2, A2A3, ..., An—1Anбарабар кесиндилерин, б. а. берилген AB кесиндини маселенин шартынанкелип чыгып канча бөлүккө бөлүү зарыл болсо, анда ошончо барабар
кесиндини коёбуз (3сүрөт, n = 6). Андан кийин AnB түз сызыгын (An чекит– акыркы кесиндинин акыры) жана A1, A2, A3, ..., An—1 чекиттер аркылууAnB түз сызыкка параллель түз сызыктарды жүргүзөбүз. Бул түз сызыктарAB кесиндини B1, B2, B3, ..., Bn—1 чекиттерде кесет жанa аны Фалестинтеоремасы боюнча n барабар бөлүккө бөлөт:AB1 =B1B2= ...= Bn—1B.Демек, ар кандай кесиндини каалаганча барабар бөлүккө бөлүүгөболот.
2маселе. ABC үч бурчтугунун BC жагы төрт барабар кесиндиге бөлүнүп, бөлүнүү чекиттери аркылуу узундугу 18 см ге барабар болгон ABжагынa параллель түрдө түз сызыктар жүргүзүлгөн. Ошол түз сызыктардын үч бурчтуктун ичинде калган кесиндилеринин узундуктарын тап.
Берилген ∠ABC дa:BB1= B1B2 =B2B3 =B3C, AB = 18 cм; B1C3||B2C2 || B3C1||AB.
Табуу керек: B1C3, B2C2, B3C1 (4сүрөт).
Чыгаруу. 1) A1B3||A2B2|| A3B1||AC жүргүзөбүз.
2) Фалестин теоремасы боюнча:
AA1 = A1A2 = A2A3 = A3B = AB:4 = 18 :4= 4,5 (cм).
2) Аныктама боюнча, AA1B3C1 төрт бурчтугу – параллелoграмм,
анткени AA1||C1B3 (шарт боюнча) жанa A1B3||AC1 (түзүү боюнча).
Демек, AA1=C1B3=4,5 (cм).
3) Аныктама боюнча, AA2B2C2 төрт бурчтугу – параллелoграмм,
анткени AA2 ||C2B2 (шарт боюнча) жана A2B2 ||AC2 (түзүү боюнча).
Демек,AA2 = C2B2 = 2AA1 = 2 ·4,5 =9 (cм).
4) Аныктама боюнча, AA3B1C3 төрт бурчтугу – параллелoграмм,ABA1 An 1 An
Bn1B1B2B3A2 A3 ..нткени AA3 ||C3B1 (шарт боюнча) жана A3B1||AC3 (түзүү боюнча). Демек,
AA3 = C3B1 = 3AA1 = 3 · 4,5 = 13,5 (cм).
Жообу: C1B3 = 4,5 cм, C2B2= 9 cм, C3B1 = 13,5 cм.
Суроо, маселе жанa тапшырмалар
1. 1) Фалестин теоремасын айт.
2) Фалестин теоремасы бурч үчүн гана орундуубу?
3) Берилген кесинди кантип n барабар бөлүккө бөлүнөт?
2. (Практикалык тапшырма.) Циркуль жанa сызгычтын жардамында берилген AB кесиндини:
1) эки; 2) үч; 3) алты; 4) жети барабар бөлүккө бөл.
3. Берилген: ∠A, AB=BD=7 cм, BC||DE, CE= 5 cм (5сүрөт).
Табуу керек: AC.
4. Берилген ∠aO b,OA=AA1=A1A2=A2A3=A3A4,
AB||A1B1||A2B2||A3B3 ||A4B4, OB4=8 cм (6сүрөт).
Табуу керек: OB1, OB2, OB3.
5. ABCD параллелoграммында M чекит BC жагынын ортосу, N чекит AD
жагынын ортосу. BN жанa MD түз сызыктар параллелoграммдын AC
диагоналын барабар үч бөлүккө бөлүшүн далилде (7сүрөт).
(6сүрөткө к.). Табуу керек: OB1, OB2, OB3.
Уйго тапшырма :23 ,Конугуулорду иштоо




















