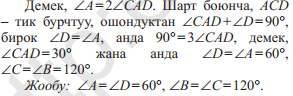Просмотр содержимого документа
«Геометрия8 Тема: Трапеция»
| Сабак 8 | Предмети: геометрия | 8-класс | 1-чейрек | Мугалим: __________ Текшерди:__________ |
| Сабактын темасы: | Трапеция |
| Сабактынтиби: | Жаңы билимди өздөштүрүү |
| Колдонулуучу усулдар жана ыкмалар: | интерактивдуу.Өз алдынча иштөө, жупташып иштөө. Өзүн-өзү баало, калыптандыруучу, диагностикалык баалоо |
| Сабакта колдонулуучу каражаттар жана материалдар: | окуу китеби, сүрөттөр, проектор, интерактивдүү доска ж.б Султанбаев “Геометрия 8-кл” |
|
| Негизги копетенттүүлүктөр:(НК 1) ,(НК 2) ,(НК 3) Предметтик компетенттүүлүк 1.Маалыматтык компетенттүүлүк (НК 1) (ПК1) 2.Социалдык коммуникативдик комп (НК 2 (ПК2)(ПК3) 3. “Өзүн өзү уюштуруу жана көйгөйлөрдү чечүү”(НК3)(ПК4) |
| Сабактын максаттары: | Көрсөткүчтөр,Күтүлүүчү натыйжалар |
|
| Билим берүүчүлүк максаты: |
|
| Трапеция жонундо тушунку алышат. Аныктамасын касиеттерин билет.Теореманы колдонуп мисалдарды иштегенди уйронушот | Мисалдарды чыгарууда касиеттерин колдонот. |
| Өнүктүрүүчүлүк максаты: |
|
| Мисалдарды чыгаруу аркылуу билим, билгичтиктерди бышыктайт.кондумдору калыптанат | Өз алдынча мисалдарды чыгаруу менен түшүндүрүп бере алат |
| Тарбиялоочулук максаты: |
|
| Тырышчаактыкка, жоопкерчиликке, кол көтөрүп сүйлөөгө тарбиялоо | Окуу куралдарын туура пайдаланууга тарбияланат |
Сабактын жүрүшү:
| Этап | убакыт | Мугалимдин иш аракети | Окуучунун иш аракети |
| Уюштуруу, | 3-мүн | | Сабакты жакшы кабыл алууга өбөлгө түзүлөт |
| 
|
| Өтүлгөн сабакты кайталап үй тапшырмаларын текшерүү жана окуучу түшүнбөй калган жерлерин кайра түшүндүрүрүп берүү | |
|
|
| Акыл гимнастикасы окуучуларга суроо: Ромб деп эмнеге айтылат? Ромбдун касиетин айт.
2) Квадрат деп эмнеге айтылат? Анын касиеттерин айт.
3) Квадратка: a) «параллелoграмм касиеттерин айтып бергиле
| Аң сезими ойгонот Ойлонот Изденет Табат |
Трапециянын аныктамасы. Бизге белгилүү болгондой, ар кандай параллелoграммда эки жуп параллель жактар болот. Эми биз бир жуппараллель жактарга гана ээ болгон төрт бурчтуктарды карап көрөбүз.
1-аныктама. Эки жагы параллель, калган эки жагы параллель болбогон төрт бурчтук трапеция деп аталат.
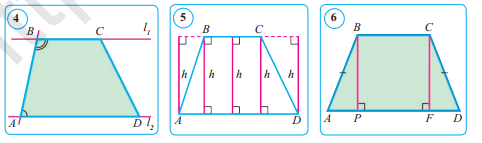
Трапециянын параллель жактары анын негиздери, параллель болбогонжактары болсо каптал жактары деп аталат. 1-сүрөттөгү ABCD трапециясында AD жанa BC жактары негиздер, AB жанa CD жактар болсо капталжактары болот.
2-аныктама. Жактарынан бири негизине перпендикуляр болгон трапецияга тик бурчтуу трапеция дейилет (2сүрөт).
3-аныктама. Каптал жактары барабар болгон трапецияга тең
капталдуу трапеция дейилет.
3-сүрөттө тең капталдуу ABCD трапециясы берилген: AB = CD.
2. Трапециянын белгиси. Эми ABCD төрт бурчтугунун трапецияболушу үчүн кандай шартты канааттандырышын карап көрөбүз.
ТЕОРЕМА:Эгерде төрт бурчтуктун бир жагына кыналган эки бурчунунсуммасы 180° ка барабар жана ага кошуна жактарга кыналган экибурчунун суммасы 180° тан айырмалуу болсо, анда мындай төрт
бурчтук трапеция болот.Далил. ABCD төрт бурчтугундa: ∠A+∠B = 180°, ∠A +∠D ≠ 180°
болсун. ABCD төрт бурчтугунун трапеция экендигин далилдейбиз.Биринчиден, бир жуп карама-каршы жактар параллель экендигин көрсөтөбүз. AB, BC (l1) жанa AD (l2) түз сызыктарын жүргүзөбүз (4-сүрөт).Шарт боюнча ∠A+∠B=180°, андa AD жана BC кесиндилерининпараллелдик белгиси боюнча параллель болот. (Эки a жанa b түз сызыктарды үчүнчү c түз сызык кескенде, ички бир жактуу бурчтардын суммасы
180° ка барабар болсо, анда a жанa b түз сызыктар параллель болот.)
Натыйжа. Трапециянын бир бурчу 90° болсо, анда анын дагы бир 90°
туу бурчу болот.
4-аныктама. Трапециянын негиздеринен биринде жаткан чекиттен экинчи негизди өзүндө камтыган түз сызыкка түшүрүлгөн перпендикуляр трапециянын бийиктиги деп аталат.
Трапециянын негиздерине перпендикуляр болгон ар кандай кесиндини
анын бийиктиги иретинде кароого болот. Ар кандай трапецияда каалаганча бийиктик жүргүзсө болот (5-сүрөт).
3. Тең капталдуу трапециянын касиети.
ABCD тең капталдуу трапециясын карап көрөбүз. Мында AD = а – чоң негиз, BC = b – кичине негиз болсун. Кичине негиздин B чокусунан BPбийиктигин жүргүзөбүз (6-сүрөт). Бийиктиктин P негизи AD негизин APжанa PD кесиндилерге бөлсүн.

Далил. C чокусунан CF⊥AD ны жүргүзөбүз. Тик бурчтуу ABP жанa DCF үч бурчтуктары барабар AB=DC ны жүргүзөбүз. Тик бурчтуу ABPжанa DCF үч бурчтуктары барабар: AB = DC – шарт боюнча, BP = CFболсо BC жанa AD параллель түз сызыктардын ортосундагы аралык болгондуктан. Үч бурчтуктардын барабардыгынан AP = FD келип чыгат. Түз
сызыктардын параллелдик белгиси боюнча, BP||CF, анткени BP ⊥ AD,
CF ⊥AD. Параллель түз сызыктардын ортосундагы аралык барабар болгондуктан, BC=PF=b. Демек,
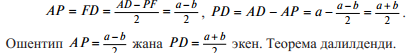
1-маселе. Тең капталдуу трапециянын негизиндеги бурчтары барабар
экендигин далилде.
Чыгаруу. ABCD – тең капталдуу трапеция, б. а. AB =DC жанa AD || BC.Тең капталдуу трапециянын AD жанa BC негиздерине кыналган бурчтарыбарабардыгын далилдейбиз (∠A=∠D, ∠B=∠C).Трапециянын кең бурчтарынын (B жанa C) чокуларынан AD негизине
перпендикуляр жүргүзөбүз: BP⊥AD, CF⊥AD (6-сүрөткө к.). Тик бурчтууABP жанa DCF үч бурчтуктар (гипотенуза жанa катети боюнчa) барабар:AB = DC – шарт боюнча, BP = CF болсо BC жанa AD параллель түзсызыктардын ортосундагы аралык болгондуктан. Үч бурчтуктардынбарабардыгынан ∠A=∠D келип чыгат.A жана B, C жана D бурчтар AD жанa BC параллель түз сызыктардын,тиешелүү түрдө, AB жанa CD кесүүчүлөр менен кесилишинен алынганички бир жактуу бурчтар, ошондуктан ∠A+∠B=180° жана ∠C+∠D= 180°.Мындан ∠B=∠C экендиги келип чыгат. Ошентип, тең капталдуу трапециянын негизиндеги бурчтары барабар экен ∠A=∠D жана ∠B=∠C.Ушуну далилдөө талап кылынган эле.
2-маселе. Тең капталдуу трапециянын кичине негизи каптал жагына
барабар, диагоналы болсо каптал жагына перпендикуляр. Трапециянын
бурчтарын тап.
Чыгаруу. Тең капталдуу ABCD трапециясы берилген, анда AD||BC,
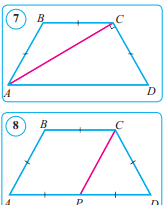
AB=BC=CD, AC⊥CD болсун (7-сүрөт). Маселенин шарты боюнча, AC
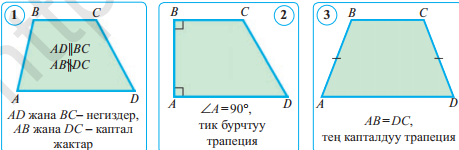
– тең капталдуу ABC үч бурчтугунун негизи, демек, ∠BCA=∠CAB. Бирoк ∠A=∠D, анткени тең капталдуу трапециянын негизиндеги бурчтарыбарабар, CAD жанa BCA бурчтар болсо AD || BC жана AC кесүүчү түзгөнички кайчылаш бурчтар болгондуктан барабар, б. а ∠CAD=∠BCA.Демек, ∠A= 2∠CAD. Шарт боюнча, ACD– тик бурчтуу, ошондуктан ∠CAD+∠D= 90°,бирок ∠D=∠A, андa 90° = 3∠CAD, демек, 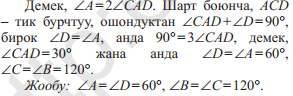
1) Кандай төрт бурчтукка трапеция дейилет?
2) Кандай трапеция: a) тең капталдуу трапеция; б) тик бурчтуу трапеция деп аталат?
2. Трапециянын чокусунан өтпөгөн бийиктиги аны эки тик бурчтуу
трапецияга бөлөт. Фигураны чийип көрсөт.
3. Тик бурчтуу трапециянын каптал жактарынын катышы 1 : 2 сыяктуу.
Трапециянын эң чоң бурчун тап.
4. Трапециянын негиздери 12 см жанa 20 см, каптал жактары болсо 4 см
жанa 11 см. Кичине негизинин чокусунан кичине жагына параллель
түз сызык жүргүзүлгөн. Ошол параллель түз сызык бөлгөн үч бурчтуктун периметрин тап.
Уйго тапшырма :§ 24