Геометрия "Презентация к урокам"

ГИА 2013 Модуль «ГЕОМЕТРИЯ»

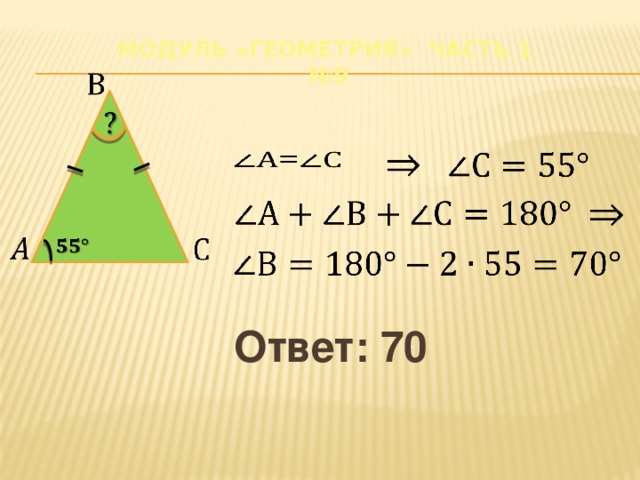
Модуль «Геометрия» часть 1 №9

Ответ: 70

Повторение

В равнобедренном треугольнике углы при основании равны

В треугольнике сумма углов равна 180°

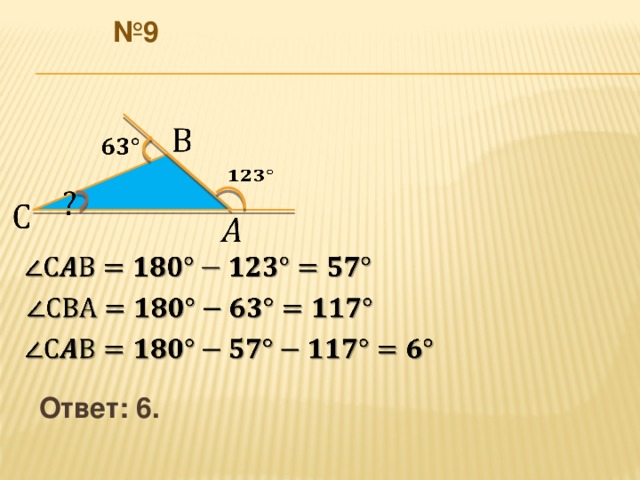
№ 9

Ответ: 6.

Повторение

Внешний угол треугольника – это угол, смежный с углом треугольника

Сумма смежных углов углов равна 180°

В треугольнике сумма углов равна 180°

№ 9

Один из углов параллелограмма на 46° больше другого. Найти больший из них.

∠ А+ ∠ D=180°

Пусть ∠А=х°, тогда ∠ D=х°+46°

х+х+46=180

2х=134

х=67

∠ D = 46+67°=113°

Ответ: 113.

Повторение

Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны.

Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°

№ 9

Найти больший угол параллелограмма АВСD.

∠ DCВ= ∠АCD+ ∠А СВ=23°+49°=72°

∠ С+ ∠ В=180°

∠ В=180°- ∠ В=180°-72°=108°

Ответ: 108.

Повторение

Если угол разделен на части, то его градусная мера равна сумме градусных мер его частей.

В параллелограмме сумма соседних углов равна 180°

№ 9

Углы ромба относятся как 3:7 .

Найти больший угол.

∠ 1+∠2=180°

Пусть х° - одна часть, тогда ∠2=3х°, ∠1=7х°

3х+7х=180

10х=180

х=18

∠ 1=18°∙7=126°

Ответ: 126.

Повторение

В ромбе противоположные стороны параллельны

Если две параллельные прямые пересечены третьей, то сумма внутренних односторонних углов равна 180°

№ 9

Разность противолежащих углов трапеции равна 68°. Найти больший угол.

∠ А+∠В=180°

∠ В+∠С

Если ∠А=х°, то ∠В=х°+68°

х+х+68=180

2х=180-68

х=56

∠ В=56° +68°=124°

Ответ: 124.

Повторение

В равнобедренном треугольнике углы при основании равны.

Сумма углов, прилежащих боковой стороне трапеции равна 180°.

№ 9

В

Найдите угол между гипотенузой и медианой, проведенной из прямого угла.

47 ⁰

D

?

С

А

∠ А+∠В=90°

Так как ∠С=∠А+∠В, то ∠В= ∠ВСD, ∠А= ∠АCD

∠ ВCD=47°

∠ ВDC=180°-2∙47 ⁰ =86 ⁰

Ответ: 86.

Повторение

В прямоугольном треугольнике сумма острых углов равна 90 ⁰

В равнобедренном треугольнике углы при основании равны

Сумма углов треугольника равна 180 ⁰

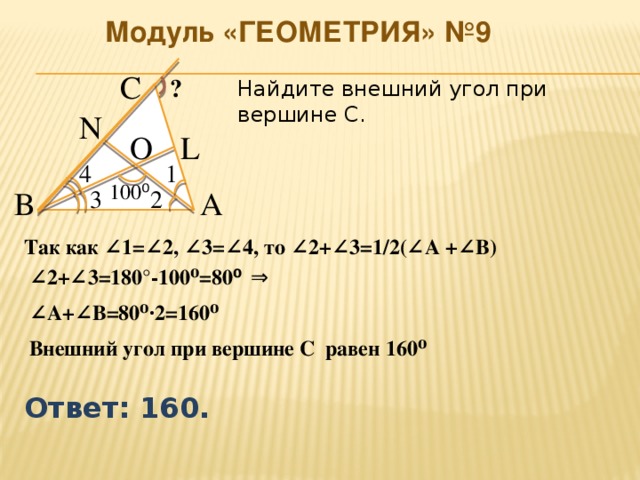
Модуль «ГЕОМЕТРИЯ» №9

С

?

Найдите внешний угол при вершине С.

N

L

О

4

1

100 ⁰

А

2

3

В

Так как ∠1=∠2, ∠3=∠4, то ∠2+∠3=1/2(∠А +∠В)

∠ 2+∠3=180°-100⁰=80 ⁰

⇒

∠ А+∠В=80⁰∙2=160⁰

Внешний угол при вершине С равен 160⁰

Ответ: 160.

Повторение

Биссектриса – это луч, который делит угол пополам

В треугольнике сумма углов равна 180°

Внешний угол треугольника – это угол, смежный с углом треугольника и он равен сумме углов треугольника, не смежных с ним.

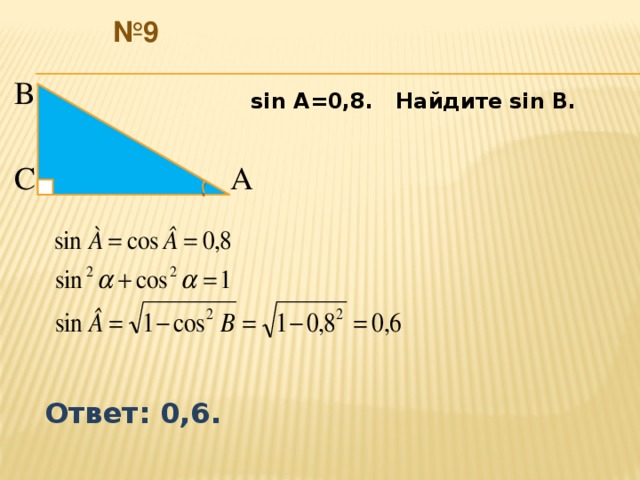
№ 9

В

sin A=0,8. Найдите sin B.

С

А

Ответ: 0,6.

Повторение

В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла

Основное тригонометрическое тождество:

Модуль «ГЕОМЕТРИЯ» №10

В

Найти АВ.

15

Повторение (2)

А

С

⇒

⇒

По теореме Пифагора

Ответ: 17.

Повторение

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Модуль «ГЕОМЕТРИЯ» №10

С

Найти AB.

120 ⁰

А

В

H

Проведем высоту CH, получим ∆ВCH.

⇒

⇒

∠ CВH=30 ⁰

∠ ВCH=60 ⁰

По теореме Пифагора в ∆BCH

Ответ: 75.

Повторение

Высота в прямоугольном треугольнике, проведенная к основанию является биссектрисой и медианой

В прямоугольном треугольнике катет, лежащий против угла в 30 ⁰, равен половине гипотенузы

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Модуль «ГЕОМЕТРИЯ» №10

В

С

Дано: параллелограмм, P=10,

1

АЕ:ЕD=1:3.

Найти AD

2

D

А

Е

3

∠ 1=∠3 как накрест лежащие при секущей ВЕ

⇒

АВ=АЕ

∠ 3=∠2 так как ∠1=∠2 по условию

Пусть АЕ=х,

тогда АВ=х, ЕD=3х

Р=2 ∙(х+4х

⇒

2 ∙(х+4х)=10

5х=5

Х=1

AD=4 ∙ 1 =4

Ответ: 4

Повторение

Биссектриса – это луч, который делит угол пополам

Периметр многоугольника – это сумма длин всех сторон многоугольника

При пересечении двух параллельных прямых накрест лежащие углы равны

Если два угла в треугольнике равны, то треугольник - равнобедренный

Модуль «ГЕОМЕТРИЯ» №10

В

АВСD – ромб. Найти меньшую диагональ.

49

А

С

О

60 ⁰

D

В ∆АОВ, где ∠ВАО=30 ⁰

⇒

ОВ=½АВ=½∙49=24,5

ВD=2ОВ=2 ∙24,5 =49

Ответ: 49.

Повторение

Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам

Катет прямоугольного треугольника, лежащий против угла в 30 ⁰ равен половине гипотенузы

Диагонали параллелограмма (ромба) точкой пересечения делятся пополам

Модуль «ГЕОМЕТРИЯ» №10

34

В

С

АВСD – трапеция, СЕ||АВ .

P ∆CDЕ =69.

Найти P трапеции

А

D

Е

Так как СЕ||АВ, то АВ=ЕС, АЕ=ВС=34

АD=АЕ+ЕD

P ∆CDЕ =CD+ЕD+СЕ

⇒

P ∆АВCD =АВ+ВС+CD+АD

P ∆АВCD =P ∆CDЕ +ВС=69+34=103

Ответ: 103.

Повторение

Если в четырехугольнике противоположные стороны параллельны, то такой четырехугольник - параллелограмм

В параллелограмме противоположные стороны равны

Если отрезок точкой разделен на части, то его длина равна сумме его частей

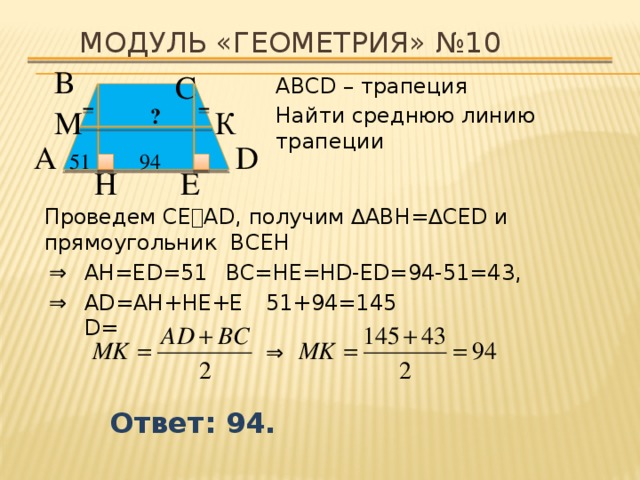
Модуль «ГЕОМЕТРИЯ» №10

В

С

АВСD – трапеция

Найти среднюю линию трапеции

К

?

М

D

А

51

94

H

E

Проведем СЕ⍊AD, получим ∆ABH=∆CED и прямоугольник BCEH

AH=ЕD=51,

BC=HE=HD-ED=94-51=43,

⇒

⇒

AD=AH+HE+ЕD=

51+94=145

⇒

Ответ: 94.

Повторение

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то треугольники равны

Если отрезок точкой разделен на части, то его длина равна сумме длин его частей

Средняя линия трапеции равна полусумме оснований трапеции

Модуль «ГЕОМЕТРИЯ» №10

В

С

АВСD – трапеция,

АВ=24, CD=30

Найти МК.

К

М

А

D

AD+BC=AB+CD=24+30=54

⇒

Ответ: 27.

Повторение

Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны

Средняя линия трапеции равна полусумме оснований трапеции

Модуль «ГЕОМЕТРИЯ» №10

Найти r.

В

r

А

С

По теореме Пифагора в ∆BCH

11

r= ½d=½АВ=½∙16=8

Ответ: 8.

Повторение

Прямой угол, вписанный в окружность опирается на диаметр окружности

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Радиус окружности равен половине диаметра

Модуль «ГЕОМЕТРИЯ» №10

В

С

АВСD – трапеция, P ∆ABCD =12. Найти боковую сторону трапеции.

5

M

К

D

А

⇒

AD+BC=2MK=2 ∙5 =10

AB= ½( P ∆ABCD -( AD+BC)) = ½( 12-10)=1

Ответ: 1

Повторение

Средняя линия трапеции равна полусумме оснований трапеции

Описать окружность можно только около равнобедренной трапеции

Периметр многоугольника – это сумма длин всех сторон многоугольника

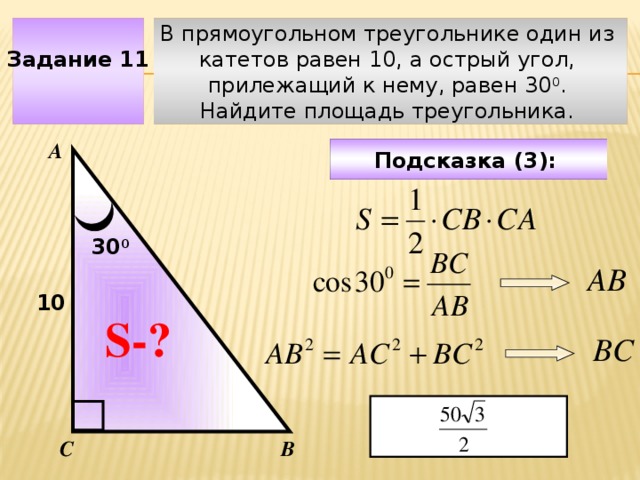
Задание 11

В прямоугольном треугольнике один из

катетов равен 10, а острый угол,

прилежащий к нему, равен 30 0 .

Найдите площадь треугольника.

А

Подсказка (3):

30 0

АВ

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S-?

ВС

В

С

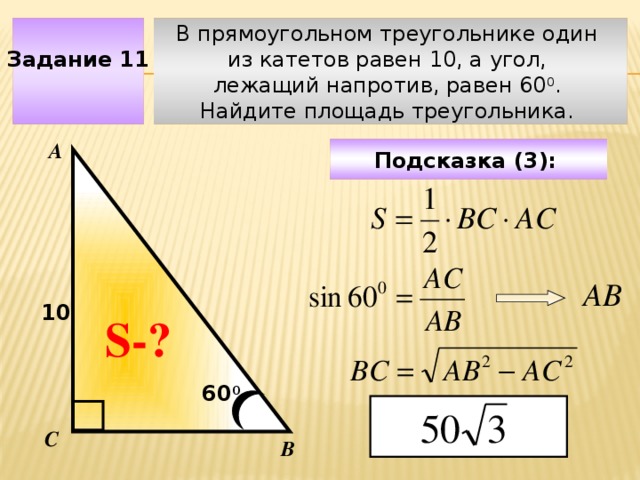
Задание 11

В прямоугольном треугольнике один

из катетов равен 10, а угол,

лежащий напротив, равен 60 0 .

Найдите площадь треугольника.

А

Подсказка (3):

АВ

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S-?

60 0

С

В

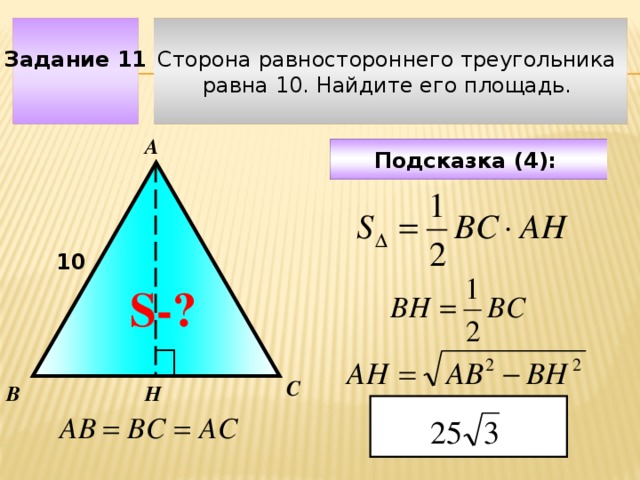
Сторона равностороннего треугольника

Задание 11

равна 10. Найдите его площадь.

А

Подсказка (4):

10

S-?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

С

Н

В

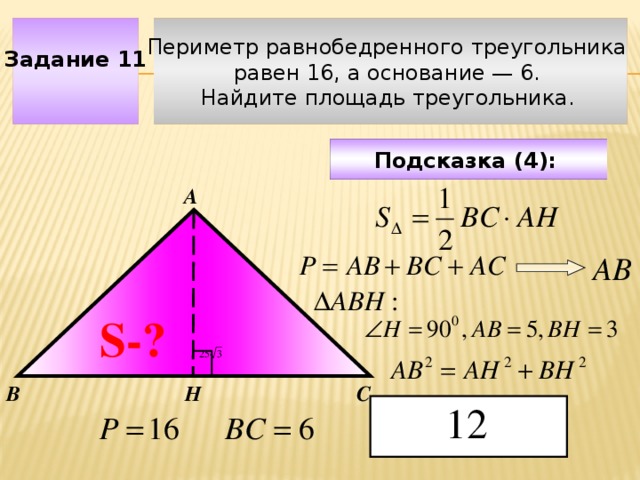
Периметр равнобедренного треугольника

Задание 11

равен 16, а основание — 6.

Найдите площадь треугольника.

Подсказка (4):

А

АВ

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S-?

Н

С

В

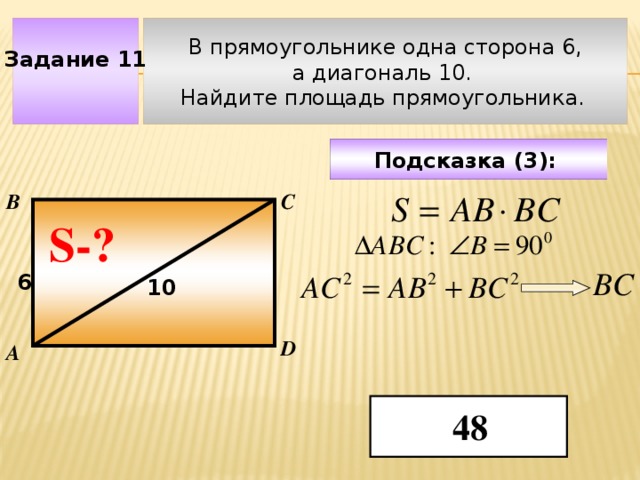
В прямоугольнике одна сторона 6,

Задание 11

а диагональ 10.

Найдите площадь прямоугольника.

Подсказка (3):

В

С

S-?

ВC

6

10

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

D

А

48

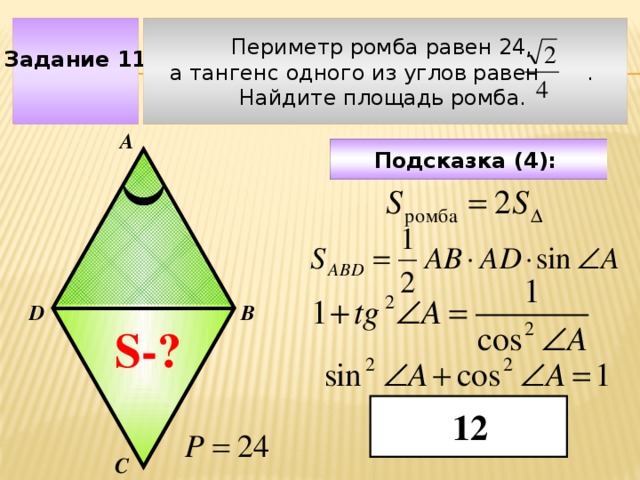
Задание 11

Периметр ромба равен 24,

а тангенс одного из углов равен .

Найдите площадь ромба.

А

Подсказка (4):

D

В

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

S-?

12

С

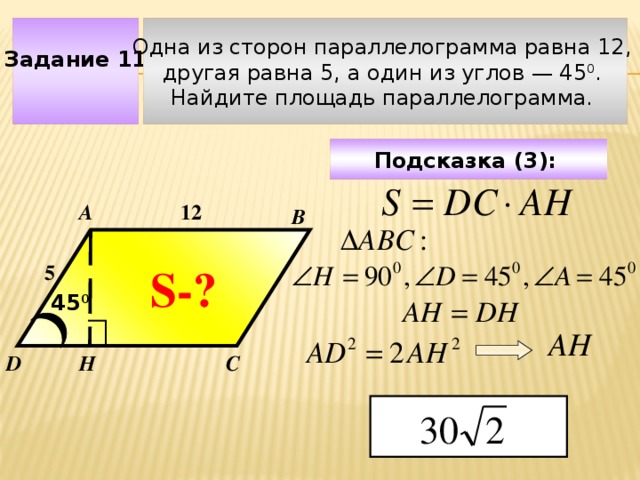
Задание 11

Одна из сторон параллелограмма равна 12,

другая равна 5, а один из углов — 45 0 .

Найдите площадь параллелограмма.

Подсказка (3):

А

12

В

S-?

5

45 0

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

АН

D

Н

С

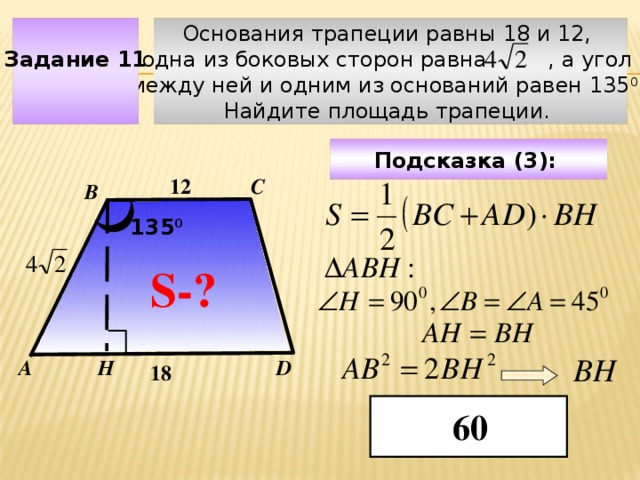
Основания трапеции равны 18 и 12,

Задание 11

одна из боковых сторон равна , а угол

между ней и одним из оснований равен 135 0 .

Найдите площадь трапеции.

Подсказка (3):

С

12

В

135 0

S-?

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

ВН

Н

А

D

18

60

Радиус круга равен 3, а длина

Задание 11

ограничивающей его окружности равна 6 π .

Найдите площадь круга.

Подсказка (3):

S-?

3

R

О

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

28,26

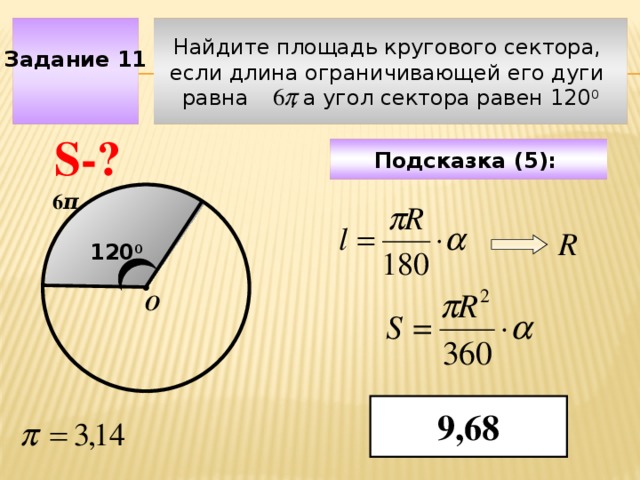
Найдите площадь кругового сектора,

Задание 11

если длина ограничивающей его дуги

равна , а угол сектора равен 120 0

S-?

Подсказка (5):

6 π

R

120 0

О

Чтобы визуализировать вопрос и ответ на задачу, необходимо щёлкнуть мышкой по пустому месту слайда; для визуализации подсказки нажмите на кнопку столько раз, сколько указано в скобках.

9,68

1. В треугольнике ABC угол C равен 90 о , AB = 10, AC = 8 . Найдите sin A .

Решение 1. В прямоугольном треугольнике ABC гипотенуза AB равна 10. Найдем катет BC . Используя теорему Пифагора, имеем BC = . Следовательно, sin A = 0,6.

Решение 2. Так как катет AC равен 8, а гипотенуза AB равна 10, то cos A = 0,8. Воспользуемся формулой , выражающей косинус через синус

острого угла. Откуда sin A = 0,6.  

Ответ. 0,6.

2. В треугольнике ABC угол C равен 90 о , высота CH равна 6, AC = 10. Найдите tg A .

Решение. В прямоугольном треугольнике ACH катет CH равен 6, гипотенуза AC равна 10. Используя теорему Пифагора, находим AH = 8. Следовательно, tg A = 0,75.

Ответ. 0,75.

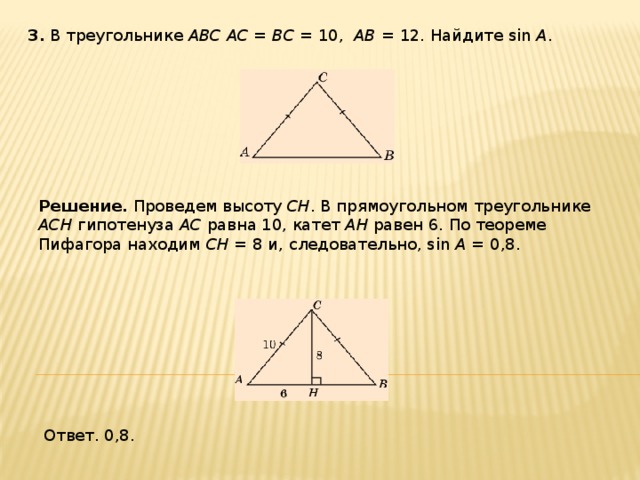
3 . В треугольнике ABC AC = BC = 10, AB = 12. Найдите sin A .

Решение. Проведем высоту CH . В прямоугольном треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По теореме Пифагора находим CH = 8 и, следовательно, sin A = 0,8.

Ответ. 0,8.

4 . В треугольнике ABC AC = BC , AB = 10, высота AH равна 8. Найдите cos A .

Решение. В прямоугольном треугольнике ABH гипотенуза AB равна 10, катет AH равен 8. По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6.

Ответ. 0,6.

5 . В треугольнике ABC AB = BC , высота CH равна 8, AC = . Найдите тангенс угла ACB .

Решение. По теореме Пифагора найдем катет AH прямоугольного треугольника ACH . Имеем AH = . Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс угла ACB равен 0,5.

Ответ. 0,5.

6 . В треугольнике ABC угол C равен 90 о , AB = 10, BC = 6 . Найдите синус внешнего угла при вершине A .

Решение. Синус внешнего угла при вершине A треугольника ABC равен синусу угла A и, следовательно, равен 0,6.

Ответ. 0,6.

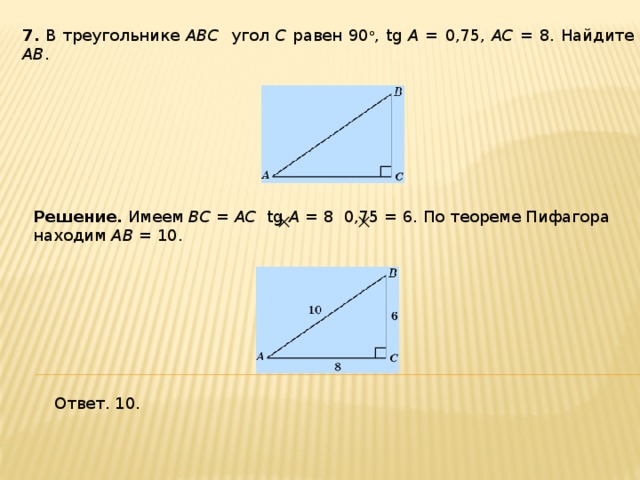
7 . В треугольнике ABC угол C равен 90 о , tg A = 0,75, AC = 8. Найдите AB .

Решение. Имеем BC = AC tg A = 8 0,75 = 6. По теореме Пифагора находим AB = 10.

Ответ. 10.

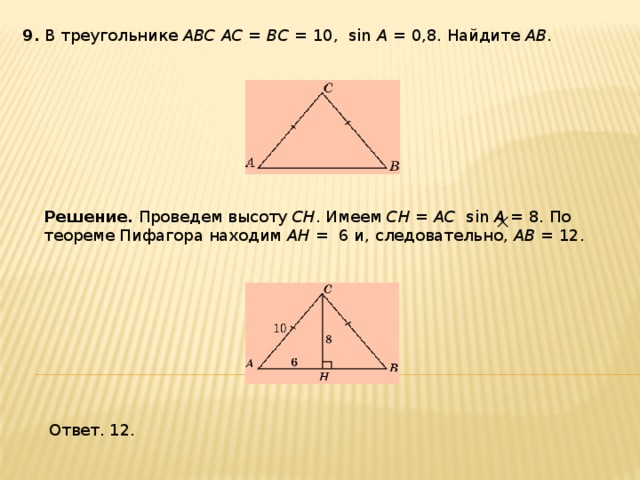
9 . В треугольнике ABC AC = BC = 10, sin A = 0,8. Найдите AB .

Решение. Проведем высоту CH . Имеем CH = AC sin A = 8. По теореме Пифагора находим AH = 6 и, следовательно, AB = 12.

Ответ. 12.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Через любые три различные точки плоскости можно провести единственную прямую.

да

нет

да

нет

2.Если угол равен 25⁰, то смежный с ним угол равен 155⁰

3.Через любую точку плоскости можно провести не менее одной прямой

да

нет

Ответ: 23.

Повторение (подсказка)

Сформулируйте аксиому о взаимном расположении прямой и точек.

Через любые две точки проходит прямая , и притом только одна

Каким свойством обладают смежные углы?

Сумма смежных углов равна 180°

Сколько прямых можно провести через точку на плоскости?

Через точку на плоскости можно провести бесконечно много прямых.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Если угол равен 56⁰, то вертикальный с ним угол равен 124⁰.

да

нет

да

нет

2.Существует точка плоскости, через которую можно провести бесконечное количество различных прямых.

3.Через любую точку плоскости можно провести не более двух прямых.

да

нет

Ответ: 2.

Повторение (подсказка)

Сформулируйте свойство вертикальных углов.

Вертикальные углы равны

Сколько прямых можно провести через точку на плоскости?

Через точку на плоскости можно провести бесконечно много прямых.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Через любые две различные точки плоскости можно провести не более одной прямой.

да

нет

да

нет

2.Через любые две различные точки плоскости можно провести не менее одной прямой.

3.Если угол равен 54⁰, то вертикальный с ним угол равен 36⁰.

да

нет

Ответ: 1.

Повторение (подсказка)

Сформулируйте аксиому о взаимном расположении прямой и точек на плоскости.

Через любые две точки проходит прямая, и притом только одна.

Вертикальные углы равны.

Сформулируйте свойство вертикальных углов.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Через любую точку плоскости можно провести прямую.

да

нет

да

нет

2.Через любую точку плоскости можно провести единственную прямую.

3.Существует точка плоскости, через которую можно провести прямую.

да

нет

Ответ: 13.

55

Повторение (подсказка)

Сколько прямых можно провести через точку на плоскости?

Через точку на плоскости можно провести бесконечно много прямых.

Существует ли точка плоскости, через которую нельзя провести прямую?

Через любую точку плоскости можно провести прямую.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.

да

нет

да

нет

2.Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 90 ⁰

3.Если при пересечении двух прямых третьей соответственные углы равны, то прямые перпендикулярны.

да

нет

Ответ: 1.

Повторение (подсказка)

Сформулируйте свойство параллельных прямых относительно соответственных углов

Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны

Сформулируйте свойство параллельных прямых относительно внутренних односторонних углов.

Если две параллельные прямые пересечены третьей прямой, то сума внутренних односторонних углов равна 180°

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.

да

нет

да

нет

2.Если при пересечении двух прямых третьей внутренние односторонние углы равны 70 ⁰ , то прямые параллельны.

3.Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны 39 ⁰ и 141 ⁰ , то прямые параллельны.

да

нет

Ответ: 1.

Повторение (подсказка)

Сформулируйте признак параллельности двух прямых относительно накрест лежащих углов.

Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов.

Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие тр-ки подобны.

да

нет

да

нет

2.Если один из острых углов прямоугольного треугольника равен 25 ⁰ , то другой угол равен 65 ⁰ .

3.Если гипотенуза и катет одного прямоугольного тр-ка соответственно равны гипотенузе и катету другого прямоугольного тр-ка, то тр-ки равны

да

нет

Ответ: 123.

55

Повторение (подсказка)

Сформулируйте признак треугольника по углам

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Каким свойством обладают острые угла прямоугольного треугольника?

Сумма острых углов прямоугольного треугольника равна 90 ⁰.

Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то треугольники равны

Повторение (подсказка)

Какие углы в равнобедренном треугольнике равны?

В равнобедренном треугольнике углы при основании равны.

Сформулируйте признак подобия треугольников по трем сторонам.

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.

Чему равна сумма углов треугольника?

Сумма углов треугольника равна 180 ⁰?

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.В∆АВС, для которого ∠А=45 ⁰ , ∠В=55 ⁰ , ∠80 ⁰ , сторона АС – наименьшая.

да

нет

2.Квадрат любой стороны треугольника равен сумме квадратов других сторон треугольника без удвоенного произведения этих сторон на косинус угла между ними.

да

нет

3.В треугольнике против меньшей стороны лежит меньший угол.

да

нет

Ответ: 23.

55

Повторение (подсказка)

Сформулируйте теорему о соотношениях между сторонами и углами треугольника.

В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.

Сформулируйте теорему косинусов.

Квадрат любой стороны треугольника равен сумме квадратов других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.В треугольнике против меньшего угла лежит большая сторона.

да

нет

да

нет

2.Центром окружности, описанной около правильного треугольника, является точка пересечения его биссектрис.

3.Кажддая сторона треугольника больше суммы двух других сторон.

да

нет

Ответ: 2.

Повторение (подсказка)

Сформулируйте теорему о соотношениях между сторонами и углами треугольника.

В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.

В какой точке лежит центр окружности, описанной около треугольника?

Центр окружности, описанной около треугольника лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.

Сформулируйте неравенство треугольника.

Каждая сторона треугольника меньше суммы двух других сторон.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (2)

1.Сумма двух противоположных углов параллелограмма равна 180 ⁰.

да

нет

2.Если в четырехугольник можно вписать окружность, то сумма его противоположных сторон равна 200, а длина третьей стороны равна 60, то длина оставшейся стороны равна 140.

да

нет

3.Около любого четырехугольника можно описать окружность.

да

нет

Ответ: 2.

55

Повторение (подсказка)

Сформулируйте свойство углов параллелограмма.

В параллелограмме противоположные углы равны.

Около какой четырехугольника можно описать окружность?

Около четырехугольника можно описать окружность, если суммы противоположных сторон четырехугольника равны.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Около любого квадрата можно описать окружность.

да

нет

да

нет

2.Сумма двух противоположных углов вписанного в окружность четырехугольника равна 90 ⁰ .

3.Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.

да

нет

Ответ: 13.

Повторение (подсказка)

Около какой четырехугольника можно описать окружность?

Около четырехугольника можно описать окружность, если суммы противоположных сторон четырехугольника равны .

Чему равны суммы противоположных углов вписанного в окружность четырехугольника?

Суммы противоположных углов вписанного в окружность четырехугольника равны 180 ⁰

Сформулируйте признак ромба с учетом того, что ромб – это параллелограмм.

Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Если в четырехугольнике диагонали равны, то этот четырехугольник – прямоугольник.

да

нет

да

нет

2.Если в четырехугольник можно вписать окружность, сумма длин двух его противоположных сторон равна 180, а длина третьей стороны равна 70, то длина оставшейся стороны равна 110.

да

нет

3.Диагонали прямоугольника равны.

Ответ: 23.

Повторение (подсказка)

Сформулируйте признак прямоугольника.

Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

В какой четырехугольник можно вписать окружность?

В четырехугольник, суммы противоположных сторон которого равны, можно вписать окружность.

Каким особым свойством обладает прямоугольник?

Диагонали прямоугольника равны.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (1)

1.В любой ромб можно вписать окружность.

да

нет

да

нет

2.Около любой трапеции можно описать окружность.

3.Если сумма двух противоположных углов четырехугольника равна 90, около этого четырехугольника можно описать окружность

да

нет

Ответ: 1.

Повторение (подсказка)

В какой четырехугольник можно вписать окружность?

В четырехугольник, суммы противоположных сторон которого равны можно вписать окружность.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Площадь круга радиуса R равна π R ².

да

нет

2.Если радиус окружности равен 10, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

да

нет

3.Длина окружности радиуса R равна π R.

да

нет

Ответ: 12.

Повторение (подсказка)

По какой формуле можно вычислить площадь круга?

S=πR²

При каком условии прямая и окружность пересекаются?

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются.

По какой формуле можно вычислить длину окружности?

С=2πR

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 6 , то эти окружности не имеют общих точек

да

нет

2.Если радиус окружности равна 3, а расстояние от центра окружности до прямой равно 2, эти прямая и окружность не имеют общих точек.

да

нет

3.Через любые три различные точки плоскости, не лежащие на одной прямой, можно провести не более одной окружности

да

нет

Ответ: 3.

Повторение (подсказка)

Каково взаимное положение двух окружностей, если расстояние между их центрами больше суммы их радиусов?

Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются.

При каком условии прямая и окружность не пересекаются?

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не пересекаются.

Можно ли через три точки плоскости провести окружность?

Через три точки плоскости можно провести окружность, если центр окружности лежит на биссектрисе угла, вершина которого лежит в одной из данных точек, стороны этого угла проходят через две другие точки, и центр окружности равноудален от данных точек.

Значит такая окружность единственная .

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Если расстояние между центрами двух окружностей меньше суммы их радиусов, то эти окружности пересекаются.

да

нет

да

нет

2.Площадь круга радиуса R равна 2 πR .

3.Длина окружности радиуса R равна 2 πR .

да

нет

Ответ: 13.

Повторение (подсказка)

Каково взаимное положение двух окружностей, если расстояние между их центрами меньше суммы их радиусов?

Если расстояние между центрами двух окружностей меньше суммы их радиусов, то окружности пересекаются.

По какой формуле можно вычислить площадь круга?

S=πR²

По какой формуле можно вычислить длину окружности?

С=2πR

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Площадь круга равна квадрату его радиуса.

да

нет

да

нет

2.Площадь круга радиуса R равна 2 πR².

3.Если вписанный угол равен 72 ⁰ , то центральный угол, опирающийся на ту же дугу окружности, равен 144 ⁰ .

да

нет

Ответ: 3.

Повторение (подсказка)

По какой формуле можно вычислить площадь круга?

S=πR²

Чему равна градусная мера вписанного угла?

Градусная мера вписанного угла равна половине дуги, на которую он опирается.

Чему равна градусная мера центрального угла?

Градусная мера центрального угла равна дуге, на которую он опирается.

Модуль «ГЕОМЕТРИЯ» №13

Укажите номера верных утверждений

Повторение (3)

1.Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности не имеют общих точек.

да

нет

2.Если расстояние между центрами двух окружностей больше суммы их радиусов, то эти окружности пересекаются.

да

нет

да

нет

3.Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти прямая и окружность пересекаются.

Ответ: 1.

Повторение (подсказка)

Каково взаимное положение двух окружностей, если расстояние между их центрами меньше суммы их радиусов?

Если расстояние между центрами двух окружностей меньше суммы их радиусов, то окружности пересекаются.

Каково взаимное положение двух окружностей, если расстояние между их центрами больше суммы их радиусов?

Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются.

При каком условии прямая и окружность пересекаются?

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются.

Модуль «Геометрия» часть 2

№ 24. В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС=6, ВС=8. Найдите медиану СК этого треугольника.

Ответ_________

№ 25. В параллелограмме АВСД точка Е-середина стороны АВ. Известно, что ЕС=ЕД. Докажите, что данный параллелограмм – прямоугольник.

№ 26 Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС. Найдите радиус окружности, вписанной в треугольник АВС.

Ответ_______

№ 24

№ 25

№ 26

Модуль «Геометрия», часть 2

24.1 Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.

25.1. Докажите, что если биссектриса одного из внешних углов треугольника параллельна противоположной стороне треугольника, то этот треугольник равнобедренный.

26.1. Площадь ромба ABCD равна 18. В треугольник ABD вписана окружность, которая касается стороны AB в точке K. Через точку K проведена прямая, параллельная диагонали AC и отсекающая от ромба треугольник площади 1. Найдите синус угла BAC .

Модуль «Геометрия», часть 2

24.2 В треугольнике ABC угол С равен , Найдите косинус внешнего угла при вершине A.

25.2. В трапеции ABCD соснованиями BC и AD диагонали AC и BD пересекаются в точке O . Докажите равенство площадей треугольников AOB и COD .

26.2. Прямоугольный треугольник ABC разделён высотой CD, проведённой к гипотенузе, на два треугольника – BCD и ACD. Радиусы окружностей, вписанных в эти треугольники, равны 4 и 3 соответственно. Найдите радиус окружности, вписанной в треугольник ABC.

Решение задания 24.1

24.1 Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.

Решение.

Решение.

A=С (какпротивоположные углыпараллелограмма), значит, A на , А=В ‒ .

A+B (по свойству параллельных прямых).

В‒ + B ,

2 В= ,

В=

Ответ.

C

B

D

A

Решение задания 25.1

25.1. Докажите, что если биссектриса одного из внешних углов треугольника параллельна противоположной стороне треугольника, то этот треугольник равнобедренный.

Решение.

Решение.

ВМ || AC , BC – секущая, , (накрест лежащие).

ВМ || AC , AD– секущая, (соответственные).

(по условию), значит,

,

по признаку – равнобедренный,

что и требовалось доказать.

D

M

B

C

A

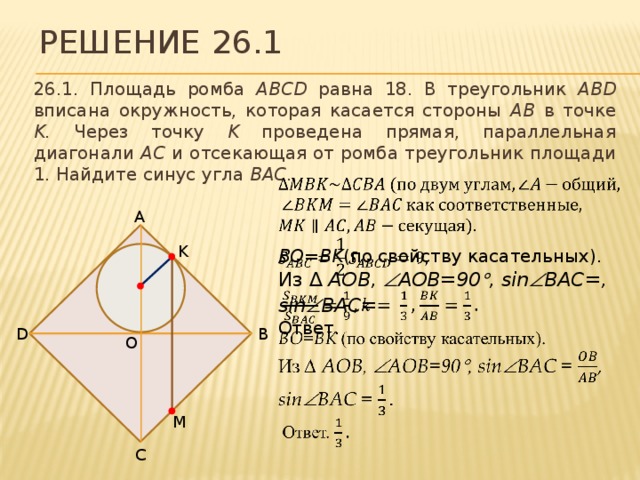
Решение 26.1

26.1. Площадь ромба ABCD равна 18. В треугольник ABD вписана окружность, которая касается стороны AB в точке K. Через точку K проведена прямая, параллельная диагонали AC и отсекающая от ромба треугольник площади 1. Найдите синус угла BAC .

BO=BK (по свойству касательных).

Из ∆ AOB,  AOB=90  , sin  BAC=,

sin  BAC=

Ответ.

A

K

D

B

O

M

C

Модуль «Геометрия», часть 2

24. Окружность проходит через вершины A и C треугольника ABC и пересекает его стороны AB и BC в точках K и E соответственно. Отрезки AE и CK перпендикулярны. Найдите  KCB , если  ABC= 20  .

25. В остроугольном треугольнике ABC проведены высоты CE и AD. Докажите, что ∆ ABD ~ ∆ CBE .

26. Диагонали четырехугольника ABCD, вершины которого расположены на окружности, пересекаются в точке M. Известно, что  ABC= 74  ,  BCD= 102  ,  AMD= 112  . Найдите  ACD.

Ссылки на источники

и использованные материалы

www.fipi.ru – ФИПИ

http://animashky.ru/index/0-16?25-10

http://animashky.ru/index/0-16?25-16

В презентации использован шаблон презентации с сайта http://pedsovet.su/

• « ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013.
• http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg
• http://www.grafamania.net/uploads/posts/2009-07/thumbs/1246640277_001.jpg