Готовимся к ЕГЭ.Основные векторные соотношения в формулах.

в.

Активизация личностной позиции учащегося в

исследовательской работе на основе субъективных новых знаний.

1. Постановка проблемы.

2. Изучение теории, посвященной данной проблематике.

3. Подбор методик исследования и практическое овладение ими.

4. Сбор собственного материала.

5. Анализ и обобщение отобранного материала.

6. Собственные выводы.

Применение векторов при решении задач планиметрии, стереометрии, физики и нестандартных задач алгебры.

Вектор – направленный отрезок.

Понятие вектора является

одним из фундаментальных понятий

современной математики.

• Геометрические утверждения можно перевести на векторный язык .
• Векторные соотношения можно истолковывать геометрически.
• Большая наглядность и простота векторных операций позволяют использовать элементы векторной алгебры при решении задач по физике и математике.
• С помощью векторов могут быть решены содержательные геометрические задачи, причем их векторные решения значительно проще и эффективнее решений средствами элементарной геометрии.

Аффинными называются свойства плоских фигур, которые сохраняются при параллельном проектировании на плоскость.

• Задачи на параллельность прямых линий
• Принадлежность трех точек одной прямой линии
• Принадлежность четырех точек одной плоскости
• Отношение отрезков параллельных прямых линий

• Сложения и вычитания векторов и его законы
• Умножение вектора на число и его законы
• Понятие коллинеарности векторов
• Разложение вектора в данном базисе
• Единственность разложения
• Свойства векторов.

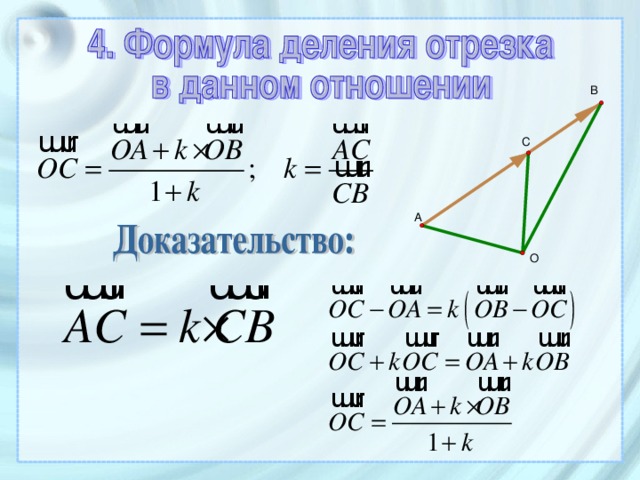
Данное соотношение можно также получить,

построив на векторах параллелограмм

Выполнение любого векторного равенства,

где точка О – произвольная точка пространства

Единственность разложения вектора по двум неколлинеарным векторам:

По определению

применяется для нахождения длины вектора.

Равенство

и

вычисляется по формуле:

Угол

между векторами

При решении метрических задач используются следующие соотношения:

:

Для ненулевых векторов

:

и

Для любых векторов

:

и

Для любых векторов

и

:

Для любых трех векторов

:

Для любых трех векторов

, считая от вершины.

Медианы треугольника пересекаются в одной точке,

которая делит каждую из них в отношении

Возьмем на медиане CD треугольника АВС точку М, такую, что

Решение.

пересечения медиан треугольника

называется его центроидом .

Точка

На сторонах АВ и АС треугольника АВС заданы

точки M и N, такие, что АМ:АВ=m, AN:АС=n.

Отрезки BN и СМ пересекаются в точке К.

В каком отношении точка К делит каждый из отрезков.

Решение.

В силу единственности разложения вектора

по двум неколлинеарным векторам

запишем равенства

Решаем систему уравнений

.

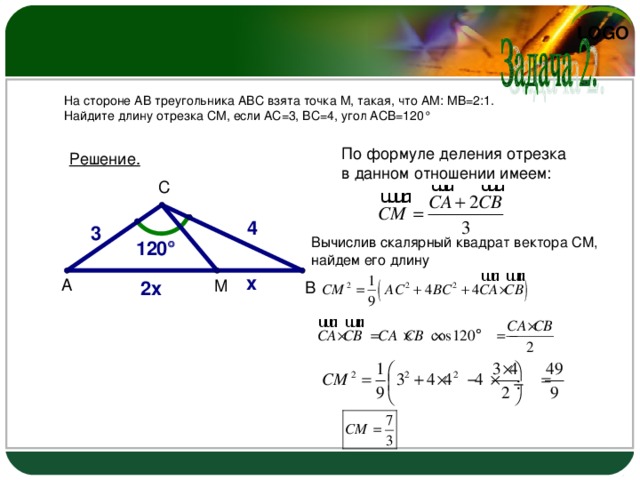
На стороне АВ треугольника АВС взята точка М, такая, что АМ: МВ=2:1.

Найдите длину отрезка СМ, если АС=3, ВС=4, угол АСВ=120 °

По формуле деления отрезка

в данном отношении имеем:

Решение.

Вычислив скалярный квадрат вектора СМ,

найдем его длину

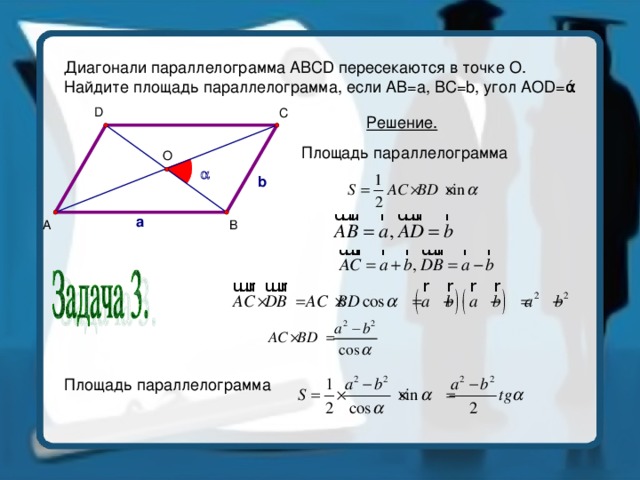
Диагонали параллелограмма ABCD пересекаются в точке О.

Найдите площадь параллелограмма, если АВ=a, BC=b, угол AOD= ά

Решение.

Площадь параллелограмма

Площадь параллелограмма

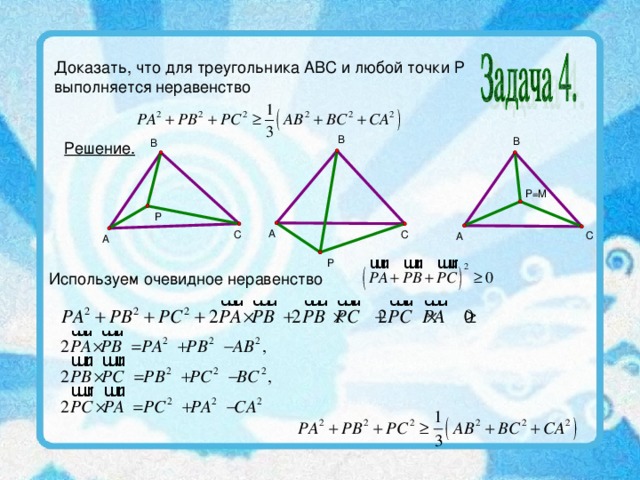
Доказать, что для треугольника АВС и любой точки Р

выполняется неравенство

Решение.

Используем очевидное неравенство

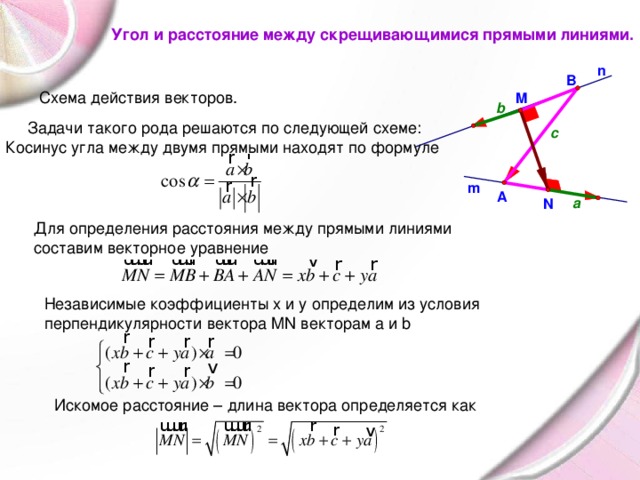
Угол и расстояние между скрещивающимися прямыми линиями.

Схема действия векторов.

Задачи такого рода решаются по следующей схеме:

Косинус угла между двумя прямыми находят по формуле

Для определения расстояния между прямыми линиями

составим векторное уравнение

Независимые коэффициенты x и y определим из условия

перпендикулярности вектора MN векторам a и b

Искомое расстояние – длина вектора определяется как

Угол и расстояние между скрещивающимися прямыми линиями.

Схема действия векторов.

Задачи такого рода решаются по следующей схеме:

Косинус угла между двумя прямыми находят по формуле

Для определения расстояния между прямыми линиями

составим векторное уравнение

Независимые коэффициенты x и y определим из условия

перпендикулярности вектора MN векторам a и b

Искомое расстояние – длина вектора определяется как

Найти расстояние и угол между скрещивающимися диагоналями

двух соседних граней с ребром длиной 1.

Решение.

Найдем модули векторов

Косинус угла между векторами

EF - наикратчайшее расстояние

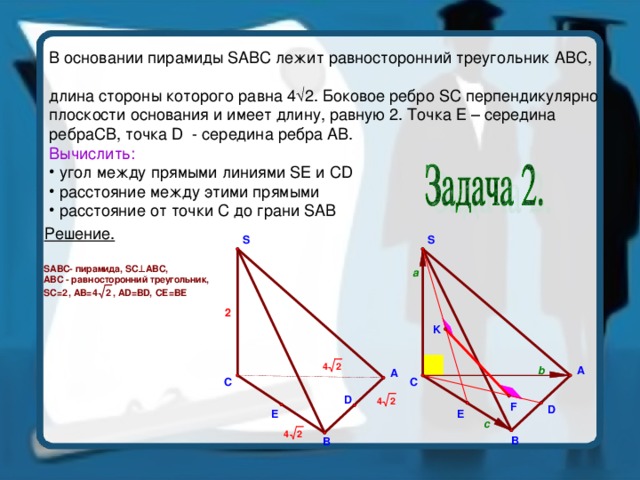
В основании пирамиды SABC лежит равносторонний треугольник ABC,

длина стороны которого равна 4 √2. Боковое ребро SC перпендикулярно

плоскости основания и имеет длину, равную 2. Точка E – середина

ребраCB, точка D - середина ребра АВ.

Вычислить:

• угол между прямыми линиями SE и CD
• расстояние между этими прямыми
• расстояние от точки С до грани SAB

Решение.

KF – расстояние между прямыми линиями SE и CD

Таблица скалярных произведений

1 . Найдем угол между прямыми линиями СЕ и CD.

2. Расстояние между прямыми линиями SE и CD

Определим коэффициенты x и y

Решим совместно систему уравнений

Запишем уравнение вектора KF

Найдем модуль вектора KF

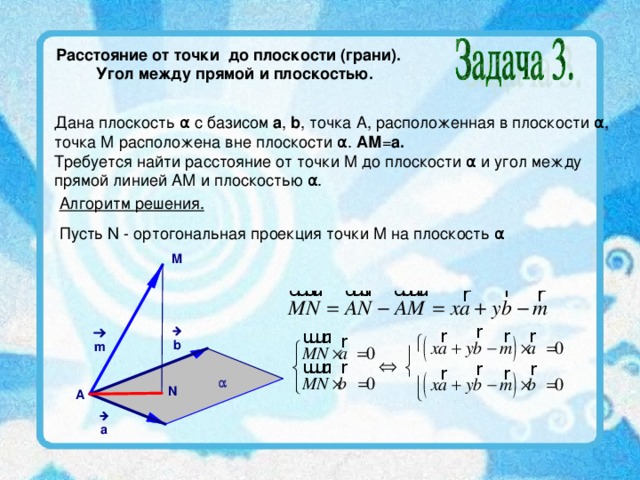
Расстояние от точки до плоскости (грани).

Угол между прямой и плоскостью.

Дана плоскость α с базисом a , b , точка А, расположенная в плоскости α,

точка М расположена вне плоскости α. АМ = a.

Требуется найти расстояние от точки М до плоскости α и угол между

прямой линией АМ и плоскостью α.

Алгоритм решения.

Пусть N - ортогональная проекция точки М на плоскость α

Условие перпендикулярности прямой АМ плоскости α

Косинус угла между прямой АМ и плоскостью α

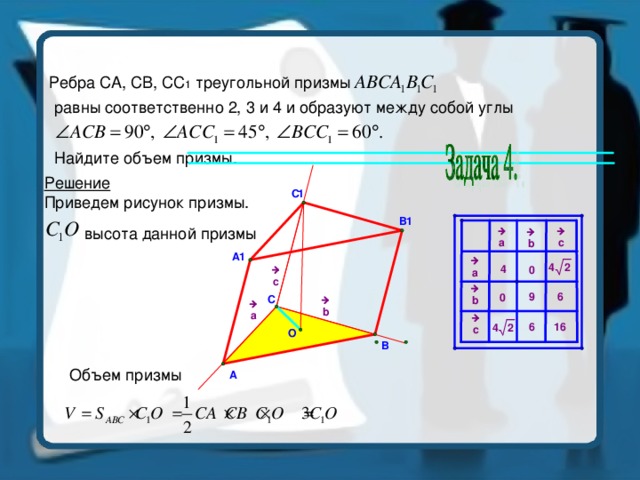
Ребра CA, CB, CC 1 треугольной призмы

равны соответственно 2, 3 и 4 и образуют между собой углы

Найдите объем призмы.

Решение

Приведем рисунок призмы.

высота данной призмы

Объем призмы

Для нахождения высоты выберем в качестве

базиса векторы

Коэффициенты x и y находим из условия перпендикулярности

Используя таблицу умножения, получим систему уравнений

Вектор

Модуль вектора

Используем таблицу умножения векторов

Дана точка М, прямая линия L с направляющим вектором а и точка А,

принадлежащая линии L AM=m

Требуется найти расстояние от точки M до прямой линии L.

Коэффициент M найдем из условия перпендикулярности

Искомое расстояние равно:

Каждое ребро призмы равно 2

Точки M и N - середины ребер AB и

Найти расстояние от точки М до прямой линии CN

Решение

Выберем базис, состоящий из векторов и

составим таблицу умножения векторов

этого базиса

Расстояние от точки M до прямой линии CN есть отрезок MP.

Точка P есть проекция точки M на прямую линию.

Поскольку прямые линии МР и CN перпендикулярны, то

Раскрывая скобки и пользуясь таблицей умножения для нашего базиса,

получаем

Искомое расстояние

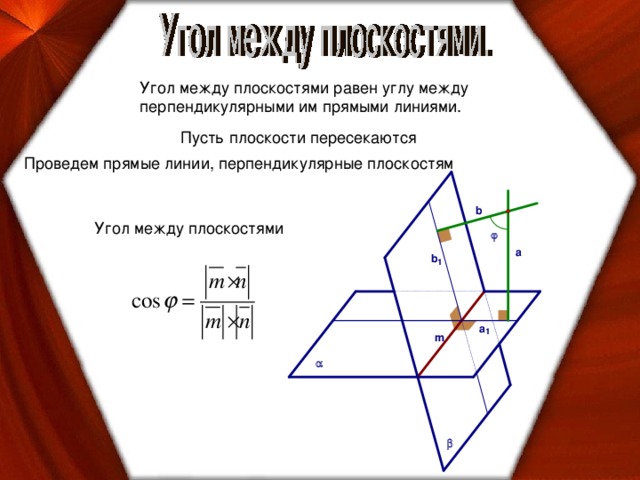
Угол между плоскостями равен углу между

перпендикулярными им прямыми линиями.

Пусть плоскости пересекаются

Проведем прямые линии, перпендикулярные плоскостям

Угол между плоскостями

В основании пирамиды SABC лежит равносторонний треугольник ABC со стороной AB=1.

Боковое ребро SA перпендикулярно плоскости основания.

Плоскость α параллельна прямым линиям SB и AC,

плоскость β параллельна прямым линиям SC и AB. Найдите угол между плоскостями

Приведем рисунок и рассмотрим базис из векторов

Решение.

Таблица умножения имеет вид, приведенный на рисунке

Угол между векторами

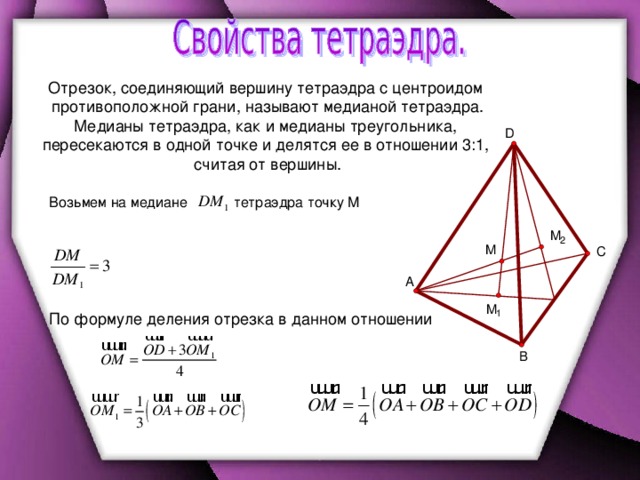
Отрезок, соединяющий вершину тетраэдра с центроидом

противоположной грани, называют медианой тетраэдра.

Медианы тетраэдра, как и медианы треугольника,

пересекаются в одной точке и делятся ее в отношении 3:1,

считая от вершины.

Возьмем на медиане

тетраэдра точку М

По формуле деления отрезка в данном отношении

Заданы углы треугольника

Доказать неравенство

Решение.

Доказать неравенство

Решение.

Дано:

Доказать

Решение.

Покажем, что сумму переменных чисел можно рассматривать

как скалярное произведение.

Введем два вектора и представим их через координаты вектора

Их скалярное произведение равно

Для скалярного произведения выполняется неравенство

По условию

Докажите, что для любых неотрицательных чисел

справедливо неравенство

Решение.

Рассмотрим векторы

Их скалярное произведение

Используем известное неравенство

Неравенство доказано

Докажите неравенство

Скалярное произведение

Модули векторов

Неравенство доказано