Графический приём введения понятия «процент» в 5 классе

Графический приём введения понятия «процент» в 5 классе

Аннотация. В статье рассматривается графический прием введения понятия «процент». Основной целью, которого является отработка умения соотносить дробь с процентами, используя графическое изображение.

У учителя может возникнуть вопрос: а как ввести понятие «процент» так, чтобы его усвоил каждый учащийся? По нашему мнению, в данной возрастной категории, восприятие учебного материала, математических объектов, в качестве которых выступают математические понятия становится продуктивнее, если учащийся видит одновременно с объяснением учителя красочные иллюстрации и прочие виды демонстрационного дидактического материала. Он быстрее и качественно запоминает то, что видел. Считаем в таких случаях целесообразно использовать графический прием введения данного понятия. Что ж, если таких задач учитель не найдет, то ему придется самому сочинить.

Введение процентов опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. С самого начала освоения понятия учащиеся выполняют много заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.

Введение нового понятия начинаем так:

- Знаете ли вы, что такое процент?

- Где в практической деятельности встречались с понятием «процент»?

Так как, понятие «процент» в 5 классе вводится после темы «обыкновенные дроби», то дети владеют навыками выделения части из целого с помощью рисунка. Поэтому без труда изображают квадрат со стороной 10 клеток на 10 и выделяют 1/100 часть квадрата по просьбе учителя, предварительно ответив на вопрос:

- Сколько всего клеток внутри квадрата? (100).

- Какая часть квадрата заштрихована? (1/100)

Остается сформулировать и озвучить, что 1\100 часть называют «процентом».

1/100=1%

- Какая часть квадрата закрашена? (2/100)

- Какой процент составляет закрашенная часть от целого? (2%)

Изображение 2% (дети закрашивают 2 клеточки) и отвечают на вопросы учителя:

- 2% это какая часть целого? (2/100) т.д.

Затем детям предлагается изобразить такой же квадрат и разделить его на две равные части и закрасить одну из них.

Дети предлагают различные варианты деления квадрата на две части.

- Закрасьте ½ часть.

- Какая дробь соответствует закрашенной части квадрата? (1/2)

- Посчитайте, сколько клеток содержится в ½ части? (50)

- Сколько процентов составляет закрашенная часть? (50%)

- Что вы можете сказать об ½ и 50%? Что они равны.

- Разделите квадрат на 4 равные части, выделите ¼ часть.

- Сколько процентов составляет дробь ¼? (25%)

- Сколько частей осталось не закрашено? (¾)

- Сколько процентов составляет дробь ¾? (75%)

Предлагаем графические задачи как одного из средств организации деятельностного подхода на уроках математики. Таким образом, формируем понятие «процент», умение анализировать реальные числовые данные, представленные с помощью графических изображений (на диаграммах).

Раздаточный материал для индивидуальных заданий:

1. Закрасьте 50% площади каждой фигуры.

1. Закрасьте 25% площади каждой фигуры.

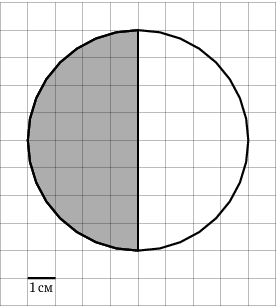
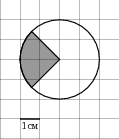
1. Сколько процентов площади составляет заштрихованная часть?

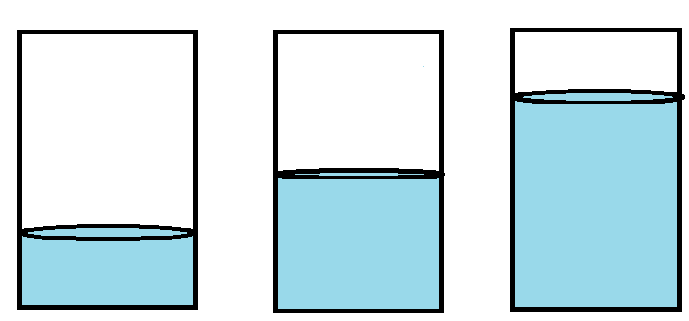
1. Определите, какой примерно процент сосуда заполнен жидкостью.

Выберите наиболее подходящий ответ:

А) 30%

Б) 50%

В) 10%

А) 25%

Б) 50%

В) 40%

А) 25%

Б) 33% в) 75%

5.

Решая такие графические задачи в течение продолжительного времени, учащиеся научатся решать эти задачи и привыкнут к понятию процента, им легче будет усвоить и решение трех основных задач на проценты.

Кроме того, при сдаче ОГЭ требуются знания, связанные с процентами, а среди заданий экзамена есть задачи на умение соотносить часть целого с процентами.

Многолетний опыт применения предлагаемого приема свидетельствует, что ученики не испытывают страха перед задачами, связанные с понятием «процент», свободно и легко переходят от графического представления к аналитическому, что несомненно способствует качественному овладению понятие «Процент».