Графическое решение неравенства с двумя переменными

Неравенства с двумя переменными

Автор: Софронова Наталия Андреевна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

( К учебнику Ю.А.Макарычева Алгебра 9

Решение неравенства

с двумя переменными

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство

( 2; 1) – решение ?

(-1; 1) – решение ?

( 2; 1) –не решение

(-1; 1) – решение

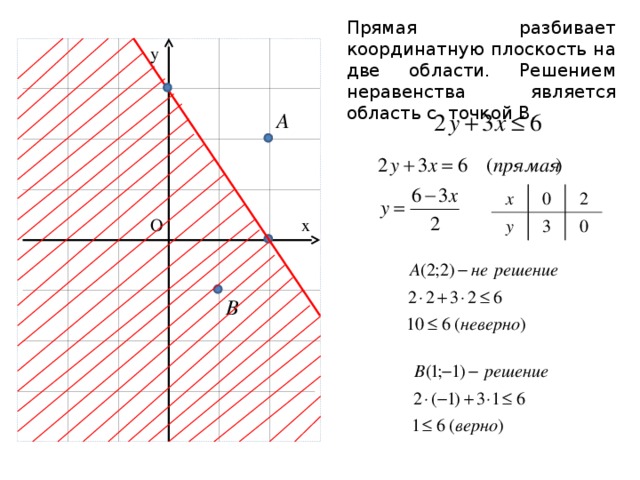
Прямая разбивает координатную плоскость на две области. Решением неравенства является область с точкой В.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

у

А

х

0

у

2

3

0

х

О

В

Изображение множества решений неравенства с двумя переменными на координатной плоскости

Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

у

у

А

О

О

О

х

В

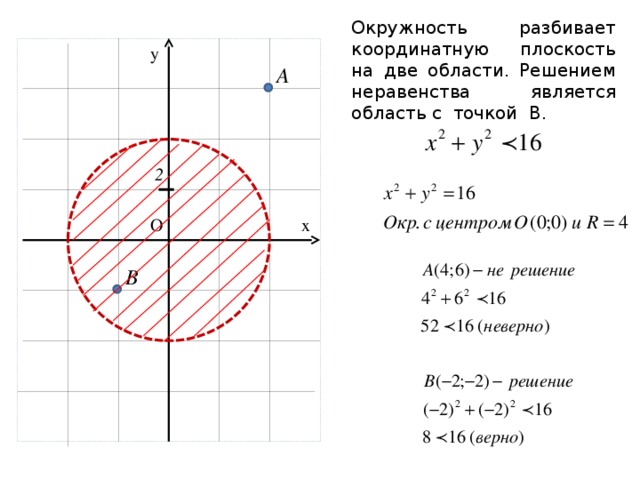
Окружность разбивает координатную плоскость на две области. Решением неравенства является область с точкой В.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

у

А

2

х

О

В

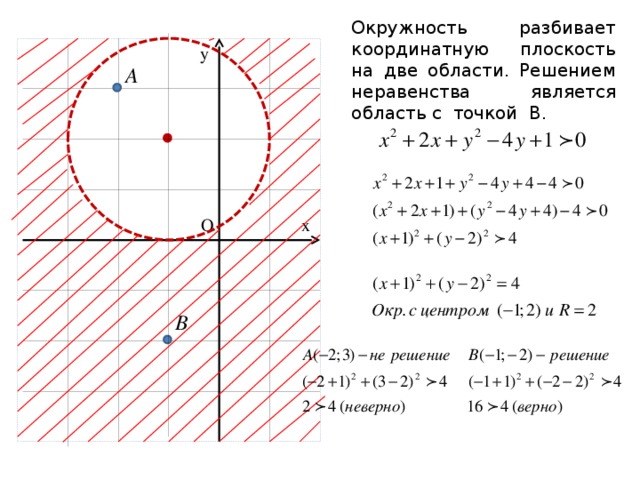
Окружность разбивает координатную плоскость на две области. Решением неравенства является область с точкой В.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

у

А

х

О

В

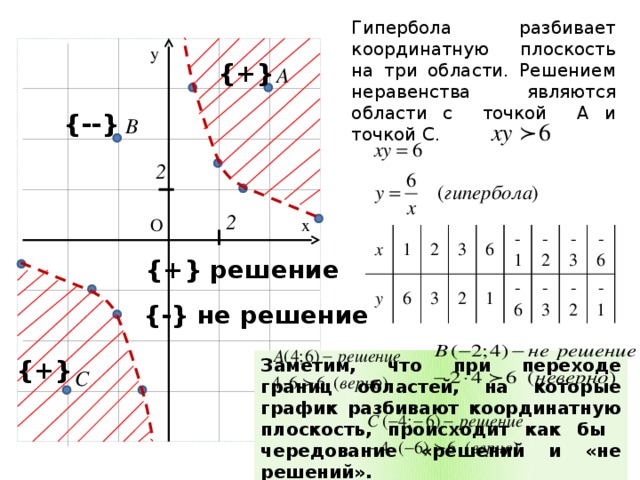
Изображение множества решений неравенства с двумя переменными на координатной плоскости

Гипербола разбивает координатную плоскость на три области. Решением неравенства являются области с точкой А и точкой С.

у

{+}

А

{--}

В

2

2

х

О

х

у

1

2

6

3

3

6

2

1

-1

-2

-6

-3

-3

-2

-6

-1

{+} решение

{-} не решение

{+}

Заметим, что при переходе границ областей, на которые график разбивают координатную плоскость, происходит как бы чередование «решений и «не решений».

С

Алгоритм решения

неравенств с двумя переменными

•   Приведем неравенство к виду f (х; у) 0;

f (х; у) ≤ 0; f (х; у) ≥ 0;)

• Записываем равенство f (х; у) = 0
• Распознаем графики, записанные в левой части.
• Строим эти графики. Если неравенство строгое (f (х; у) 0), то – штрихами, если неравенство нестрогое (f (х; у) ≤ 0 или f (х; у) ≥ 0), то – сплошной линией.
• Определяем на сколько частей графики разбили координатную плоскость
• Выбираем в одной из этих частей контрольную точку. Определяем знак выражения f (х; у)
• Расставляем знаки в других частях плоскости с учетом чередования ( как по методу интервалов )
• Выбираем нужные нам части в соответствии со знаком неравенства, которое мы решаем, и наносим штриховку

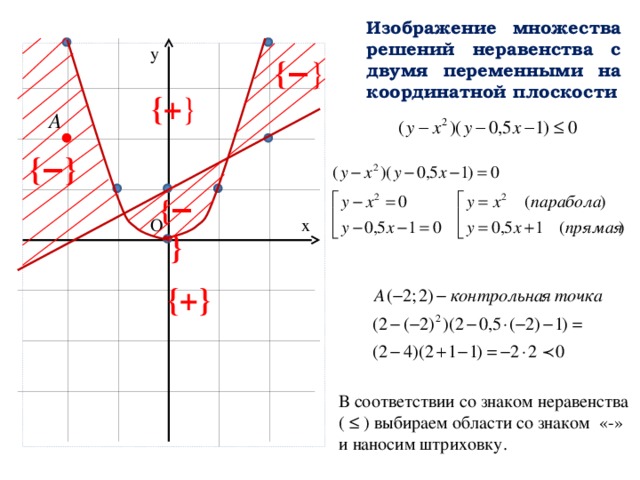
Изображение множества решений неравенства с двумя переменными на координатной плоскости

у

{ ‒ }

{+ }

А

{ ‒ }

{ ‒ }

О

х

{+}

В соответствии со знаком неравенства ( ≤ ) выбираем области со знаком «-» и наносим штриховку.

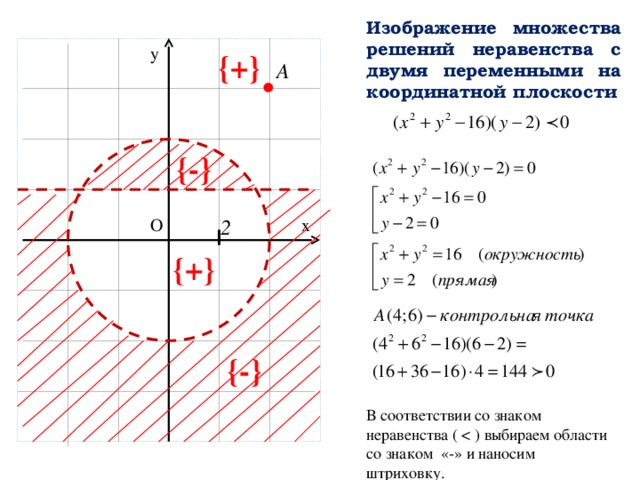
Изображение множества решений неравенства с двумя переменными на координатной плоскости

у

{+}

А

{-}

х

2

О

{+}

{-}

В соответствии со знаком неравенства (

Изобразите на координатной плоскости

множество решений неравенств: