График и свойства функции у=sinx

6 декабря

Классная работа

« Природа формирует свои законы языком математики.»

Г.Галилей.

27.09.23

Свойства и график функции у=sinx

27.09.23

Найдите

• Вычислите:

sin 0= sin =

cos = cos 0 =

sin = sin =

tg = tg =

sin = sin =

27.09.23

Вспомним

2. Как при момощи графика функции построить графики функций (робота в команде):

27.09.23

Вспомним

3. Найдите наименьший положительный период функции:

у = cos 4x y = cos x /4

27.09.23

С помощью тригонометрического круга

построим график функции y = sin x

на отрезке [0 ;2 π ]

у

у

х

График ом функции y = sin x кривая , которая называется

СИНУСОИДА

27.09.23

Свойства функции y = sin x

Область определений D (sin x)= R

Область значений E(sin x) = [-1; 1]

у

х

8

27.09.23

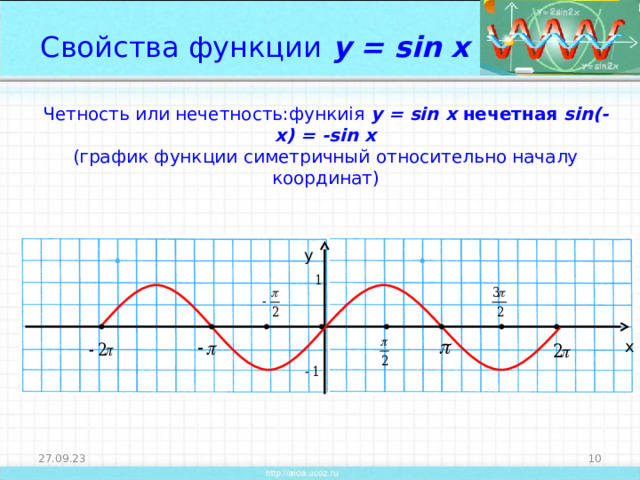
Свойства функции y = sin x

Четность или нечетность:функиі я y = sin x нечетная sin (- x) = - sin x (график функции симетричный относительно началу координат)

у

х

9

27.09.23

Свойства функции y = sin x

Периодичность: функция y = sin x пери о дичная с наименьшим положительным периодом T = 2   sin ( x + 2  ) = sin x

у

х

10

27.09.23

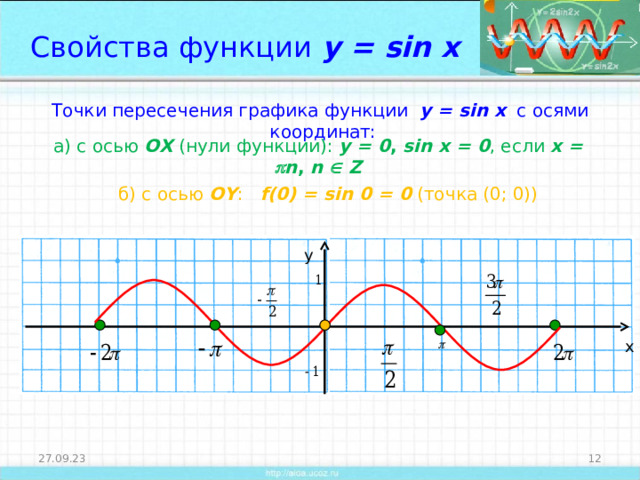
Свойства функции y = sin x

Точки пересечения графика функции y = sin x с осями координат:

а) с осью ОХ (нули функции ): у = 0 , sin x = 0 , если х =  n , n  Z

б) с осью О Y : f(0) = sin 0 = 0 ( точка (0; 0) )

у

х

11

27.09.23

0, якщо х  ( 0 + 2  n;  + 2  n), n  Z sin x якщо x  (  + 2  n; 2  + 2  n), n  Z у х 12 27.09.23 " width="640"

Свойства функции y = sin x

Промежутки знакопостоянства :

sin x 0, якщо х  ( 0 + 2  n;  + 2  n), n  Z

sin x якщо x  (  + 2  n; 2  + 2  n), n  Z

у

х

12

27.09.23

Свойства функции y = sin x

Промежутки монотонности:

а) функция возрастает на каждом промежутке : x  [-  /2 + 2  n ;  / 2 + 2  n ] , n  Z

б) функция спадает на каждом промежутке : x  [  /2 + 2  n ; 3  / 2 + 2  n ] , n  Z

у

х

27.09.23

13

14

Свойства функции y = sin x

Экстремумы функции:

Х мах =  / 2 +  n , n  Z , Y мах = 1

Х м in = -  / 2 + 2  n , n  Z, Y м in = -1

у

х

14

27.09.23

Выполните усно:

• Какие из точек пренадлежат графику функции

15

27.09.23

Выполните усно:

2 . Найдите наименьший положительный период функции:

у = 3sin9x y = -0 , 5sin x / 2

27.09.23

15

Выполните усно:

3 . Как при помощи графика функции

построить графики функций:

27.09.23

15

y=sin x +1

y=sin x – 0 , 5

Постройте графики функций:

у=sin x +1

у=sin x — 0,5

у

х

у

х

15

27.09.23

y=sin ( x – )

y=sin ( x + )

Постройте графики функций:

у=sin (x - )

у=sin (x - )

у

х

у

х

19

27.09.23

Постройте графики функций:

1. Поcтройте график функции

2. Постройте график функции

3. Побстройте график функции

у

х

27.09.23

20

Ваши впечатления об уроке

• Оправдались ли ваши ожидания от урока?

• Что понравилось на уроке?

• Что не понравилось на уроке?

27.09.23

21

27.09.23

21

Домашнее задание:

1) Выучить свойства функции у = sin x ; 2) Построить графики функций и описать их свойства

27.09.23

21

21