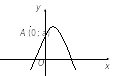Кыргызстан, Бишкек
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 28.03.2025 13:03
Нуруева Жаңыл Болотовна
Преподаватель математики
53 года
13 515
2 819 
Местоположение
Специализация
Ийри сызыктуу трапециянын аянты
Категория:
Алгебра
09.03.2020 21:29
Просмотр содержимого документа
«Ийри сызыктуу трапециянын аянты»
| №___Сабактын планы | Группа __________ | Курс -1 |
| Дициплина | Математика (Алгебра) | Мөөнөтү “____”___________ 20__ жыл |
Сабактын тиби: жаңы билимдерди өздөштүрүү
Сабактагы колдонулуучу усулдар жана ыкмалар: интерактивдуу, өз алдынча иштөө, жупташып иштөө. мээге чабуул ж.б.
Сабакта колдонулуучу каражаттар жана материалдар: окуукитеби, сүрөттөр, компьютер, проектор, интерактивдүү доска ж.б
| Сабактын максаттары | Күтүүлүүчү натыйжалар | |
| Билим берүүчүлүк | Аныкталган интегралды табат | Талицаны пайдаланып мисалдарды чыгарат |
| Өнүктүрүүчүлүк | Ийри сызыктуу трапециянын аянтын табат | Жогорку предел тмнк прелди айымалап , ордуна коюну уйронот |
| Тарбиялык | Тырышчаактыкка, жоопкерчиликке, кол көтөрүп сүйлөөгө тарбиялоо | Окуу куралдарын туура пайдаланууга тарбияланат |
Негизги компетенттүүлүктөр: Предметтик компетенттүүлүктөр:
1.Маалыматтык компетенттүүлүк (НК 1) 1. Эсептөө (ПК 1)
2.Социалдык коммуникативдик комп (НК 2) 2. Аналитикалык-функционалдык (ПК 2)
3. “Өзүн өзү уюштуруу жана көйгөйлөрдү чечүү” (НК 3) 3. Көрсөтмөлүү-образдуу (ПК3)
Сабактын жүрүшү:
| Этап | убакыт | Мугалимдин иш аракети | Окуучунун иш аракети | Компетенттүүлүк, баалоо | |||
| ((НК) | ( ПК) | ||||||
| Уюштуруу, |
| Уюштуруу. Саламдашуу | Саламдашат |
|
|
| |
|
|
| № Окуучуларды толуктоо, тазалыкка көңүл буруу, окуучуларды активдештирүү. Логикалык суроолорду берүү. “Акылды өркүндөтүү үчүн математиканы окуу керек”-деген сөз кайсы математик окумуштууга тиешелүү 9-класста сен окуган алгебра китебинин автору ким? Эки киши 5 метр карагайды бир минутадан араалашты.Ар бир жолу араалоосу 1,5 минутага созулду.Карагайды канча минутада араалап бүтүштү? |
|
|
|
| |
| Жаны тема |
|
| НК 1 НК 2 НК 3
| ПК 1 ПК 2 ПК 3 |
| ||
| |
| ||||||
| Кошумча конугуулор |
| ||||||
| Бышыктоо |
| НК 2 НК 3 | ПК 2 ПК 3 |
| |||
| Үй тапш |
| №37 | НК 1 НК 3 | ПК 1 ПК 3 |
| ||
| Жыйын-тоо. Баалоо |
| 1.Теманы бышыктоо үчүн суроолор берилет 2.Талкуу 3.Баалоо 4.Үй тапшырма берилет . | Окуучулар өз жөндөмдүүлүктөрү менен жазган иштерин жактап беришет.. | НК 1 НК 2 НК 3 | ПК 1 ПК 2 ПК 3 |
| |
1. Эгерде жогорудагы сүрөттө берилген 
тик бурчтуу координаталар системасында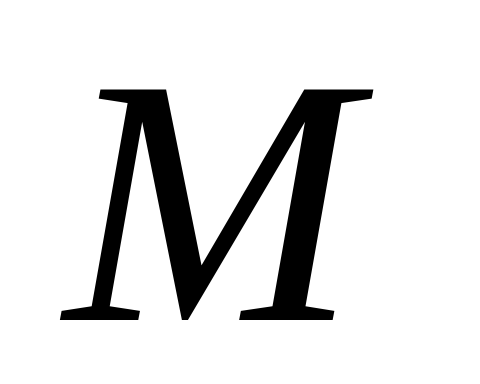 
чекити (2,3; 2,1) координаталарына ээ болсо, анда төмөн жактагылардын кайсынысы 
чекитинин координаталары болуп эсептелет?
(2,4; 1,9)
(2,5; 2,1)
(2,6; 2,2)
(2,1; 2,4)
(2,0; 2,0)
Чыгарылышы.
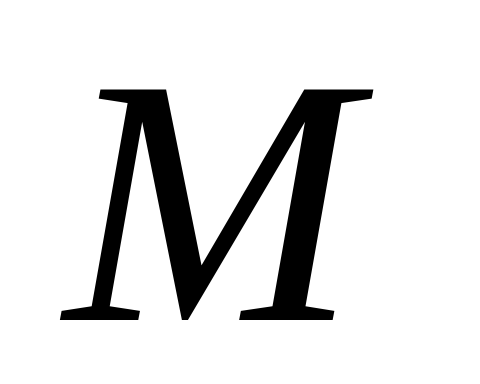Координаталар тегиздигиндеги чекити чекитинин оң жагында, андан өйдөрөөк жайгашкан. Андай болсо, чекитинин координаталары 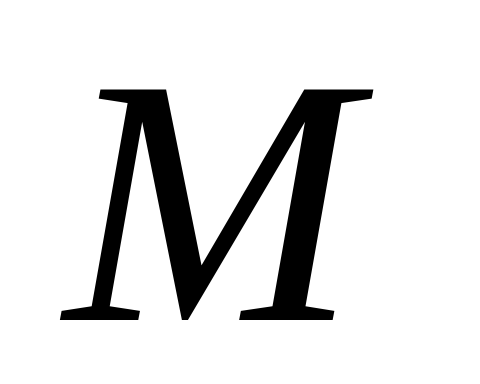чекитинин тийиштүү координаталарынан чоң болушу керек. Т.а. чекитинин абсциссасы 2,3 санынан чоң болушу керек. Ошон үчүн Г жана Д жоопторун алып салса болот. Калган жооптордун ичинен ордината 2,1ден чоң болгон жоопту тандайбыз. Бул – В жообу. Туура жооп: В.
2. Эгерде 
, ал эми 
болсо, анда 
2
1
–1
–2
–4
Чыгарылышы.
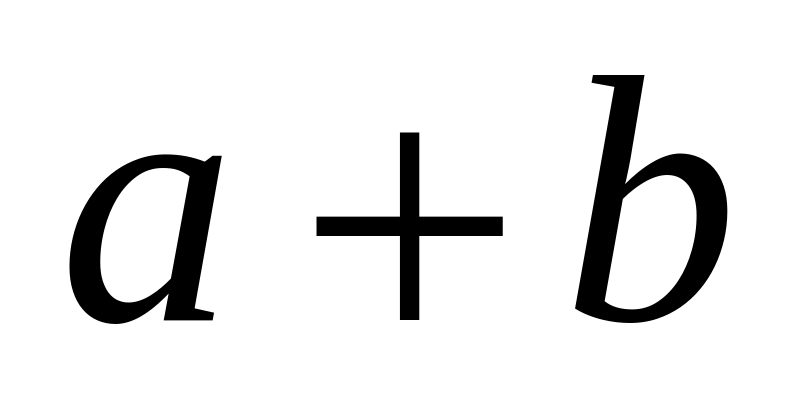-нын ордуна 
санын коюп,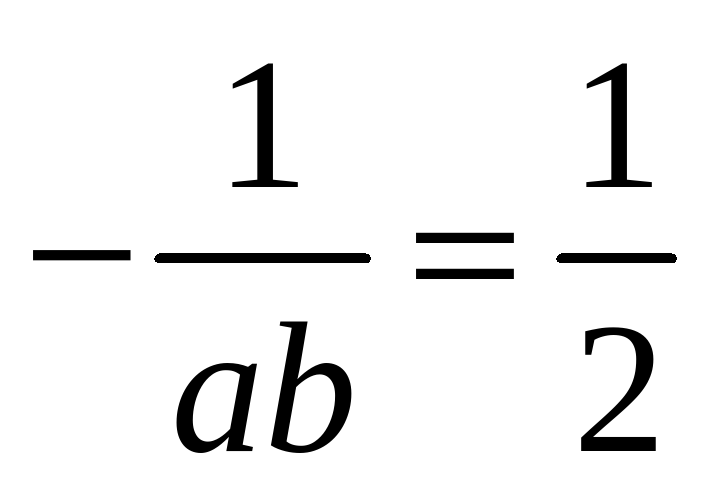 
барабарсыздыгын алабыз. Андай болсо, 
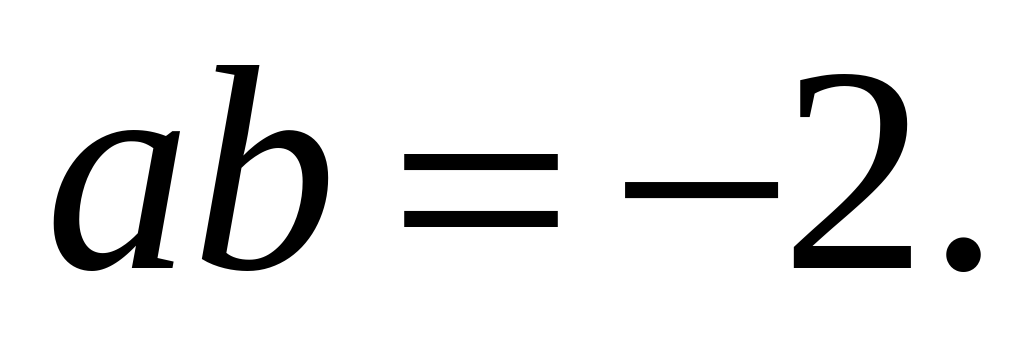Туура жооп: Г.
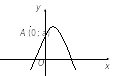
3. Эгерде Oxy тик бурчтуу координаталар системасында функциясынын графиги тартылган болсо, анда
3
3,5
4
4,5
5
Чыгарылышы.
– функциянын графиги ординаталар огун кесип өткөн чекит болгондуктан, чекитинин координаталары парабола теңдемесинин шартына туура келет, демек, теңдемеси аткарылып, болот.
Туура жооп: А.
4. Бардык үчүн функциясы формуласы менен берилген. Эгерде мааниси бүтүн сан болуп эсептелсе, анда төмөн жактагы сандардын кайсынысына барабар?
Чыгарылышы.
Туура жоопту -тин сунуш кылынган бүтүн терс маанилеринин ичинен тандап жатып, эки чен-өлчөмдү эске алабыз:
3кө бөлүнөт,
так квадрат болуп эсептелет.
Биринчи чен-өлчөмгө эки сан гана туура келет: жана Алардын ичинен саны үчүн гана анын карама-каршысы – так квадрат болот.
Чындыгында эле, шартында функциянын мааниси бүтүн сан болот :
Туура жооп: В.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
