Министерство здравоохранения Кузбасса
Государственного бюджетного профессионального образовательного учреждения
Новокузнецкий филиал
«Кузбасский медицинский колледж»
Специальность 34.02.01
Сестринское дело
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по дисциплине
«Математика»
по теме
«Тела вращения в медицине»
Обучающийся _____________________ Политова Марина Константиновна
(подпись) (ФИО)
Преподаватель ____________________ Шилепина Надежда Ивановна
(подпись) (ФИО)
Индивидуальный проект защищен:
«___» ____________ 20__ г.
Оценка _________________
НОВОКУЗНЕЦК, 2021
Оглавление
ВВЕДЕНИЕ 3
ГЛАВА 1. Теоретические аспекты ГЕОМЕТРИЧЕСКИх ФИГУр 6
1.1 Определения тел вращения. Формулы вычисления площадей и объемов 6
1.2 Зачем нужно измерять органы и конечности 10
Глава 2. Практические расчеты объема и веса руки 12
2.1 Вычисление веса руки 12
2.2 Вычисление площади руки 15
ЗАКЛЮЧЕНИЕ 18
СПИСОК источников 19
ВВЕДЕНИЕ
Мой проект называется «Тела вращения в медицине», а связано это с тем, что моей будущей профессией будет медицина, ведь она всегда является неотъемлемой и незаменимой частью человечества, всегда востребована в обществе. Мне известно много примеров, в которых с медициной тесно связана алгебра, например: врач - статистик, лаборант, фармацевт, тканевый инженер и др., но я ни разу не встречалась с геометрией в этом разделе науки. В самом начале моего проекта я провела работу в поиске информации о математике, как науке, о её присутствии в разных сферах деятельности человека. И была крайне удивлена тем, что в каждой профессии математика присутствовала в той или иной степени. Не зря говорят: математика - царица наук. Числами можно выразить все, что есть в нашем мире! И медицина не исключение.
Далее, находя информацию о связи геометрии с телом человека, я обнаружила целый мир удивительных открытий. Анатомия человеческого тела очень многогранна. В ней имеется множество различных элементов, отличающихся по местоположению, форме и составу. Для того чтобы дать более точное описание органу, структуре или образованию, в 19 веке в анатомию были введены такие геометрические понятия, как оси и плоскости. Благодаря установленной таким образом симметрии человеческого тела, облегчилось понимание его строения.
Геометрия играет в анатомии человека и другую очень важную роль: Многие элементы тела человека получили свои названия из-за схожести с геометрической фигурой. Например, при классификации суставов человека по форме применялись ассоциации схожести с геометрическими фигурами: данных суставов уже можно получить представление об их форме, мышц, костей и т.д. Таким образом, в анатомической терминологии фигурирует очень много терминов, связанных с такой наукой, как геометрия.
О строении тела человека многое известно благодаря науке анатомии. В этой сфере были проведены и проводятся по сей день разные исследования: измерения, сравнения и т.д. Выведены и составлены таблицы среднестатистических показателей, чтобы те люди, которые связаны с медициной, могли использовать эти данные в своей работе.
Увидев такую тесную связь геометрии с анатомией, я решила вычислить объем моей руки от пальцев до плеча и её площадь с помощью своей формулы и сравнить полученные вычисления с информацией из медицинских справочников.
Актуальность проекта: данный проект развивает у студентов исследовательские навыки, что способствует раскрытию творческих способностей.
Цель проекта: исследовать возможности применения геометрии в вычислении параметров тела человека.
Задачи проекта
Изучить медицинскую литературу по теме проекта.
Систематизировать изученный материал.
Провести измерения органов и частей тела человека.
Выполнить расчеты по своим формулам.
Сравнить полученные результаты с практическими данными из медицинских справочников.
Объект и исследования: тело человека.
Предмет исследования: тела вращения в медицине.
Гипотеза: с помощью геометрических законов можно рассчитать конкретные параметры органа или части тела с допустимой точностью.
Методы исследования:
Изучение и обобщение, анализ литературы по теме проекта.
Наблюдение, измерение, расчет и анализ полученных данных.
Объем и структура индивидуального проекта: композиционный состав – введение, 2 главы, заключение, 6 использованных информационных источников, 6 таблиц, 7 рисунков, 9 формул.
Период исследования:
Выбор темы – октябрь;
Составление графика этапов – ноябрь;
Представление итога работы – апрель;
Сбор материала – ноября – январь;
Работа над поставленными целями, задачами. Создание доклада и презентации – ноябрь-март;
Подведение итогов, формулирование выводов, оформление презентации – март;
Подготовка к выступлению с докладом – апрель
ГЛАВА 1. Теоретические аспекты ГЕОМЕТРИЧЕСКИх ФИГУр
Первичные данные о свойствах тел вращения характерны к времени зарождения геометрии как дальнейшей математической науки. Строгие доказательства теорем, служащих для вывода формул тел вращения изложены в книге «Начал» Евклида.
Различные объемы тел вращений, боковая поверхность конуса, цилиндра были открыты в 3 в. до н. э. Архимедом. Одна из причин развития геометрии, была задача на вычисления объёмов, идущая из практических потребностей
Определения тел вращения. Формулы вычисления площадей и объемов
Конус – поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса) «рисунок 1».
Если направляющая конуса – замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют конусом, а внутренность этой кривой называют основанием конуса.
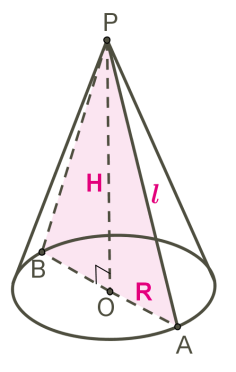
Рисунок 1 – Конус
Объём конуса вычисляют по формуле:
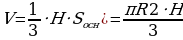 (формула 1), где
(формула 1), где
π – число «пи», берем равным 3,1415;
R – радиус конуса;
H – высота конуса;
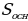 – площадь основания конуса.
– площадь основания конуса.
Усечённый конус или конический слой – часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием «рисунок 2».
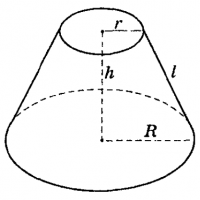
Рисунок 2 – Усеченный конус
Объем усечённого кругового конуса (не обязательно прямого) равен:
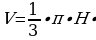 (R2 +R∙r+r2) (формула 2), где:
(R2 +R∙r+r2) (формула 2), где:
π – число «пи», берем равным 3,1415;
R – большой радиус усеченного конуса;
r – малый радиус усеченного конуса.
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны.
Объем трапеции находится по формуле:
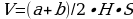 , (формула 3) где:
, (формула 3) где:
Н – высота трапеции;
a – длина большого основания;
b – длина малого основания;
S – толщина трапеции.
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
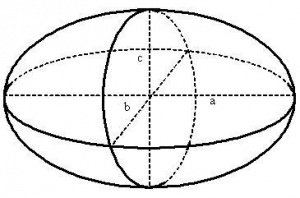
Рисунок 3 – Эллипсоид
Объем эллипсоида находится по формуле:
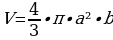 , (формула 3) где:
, (формула 3) где:
а – горизонтальная полуось,
b – вертикальная полуось,
π – число «пи», возьмем равным 3,1415.
Для сплюснутого эллипсоида, а b.
Цилиндр (др.-греч. Κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её «рисунок 4».
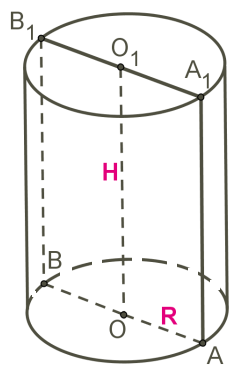
Рисунок 4 – Цилиндр
Объем цилиндра находится по формуле:
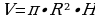 , (формула 4), где:
, (формула 4), где:
π – число «пи», равное 3,1415;
R – радиус цилиндра;
Н – высота цилиндра.
Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного «рисунок 5».
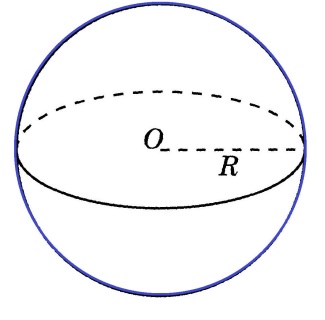
Рисунок 5 – Шар
Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.
Объем данного шара находится по формуле:
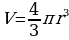 (формула 8), где
(формула 8), где
π - число «пи», = 3,1415;
r - радиус шара.
В медицине, кроме объема, часто используется площадь геометрических фигур, например, врачами – комбустиологами. Для дальнейших расчетов я воспользовалась следующими формулами:
Площадь цилиндра: 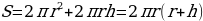 , (формула 5), где
, (формула 5), где
π - число «пи», берем равное 3,1415;
r - радиус основания;
h - высота цилиндра.
Площадь усеченного конуса: 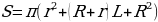 (формула 6), где:
(формула 6), где:
π - число «пи», = 3,1415;
r - радиус вращения;
L - образующая конуса.
Площадь объёмной трапеции: 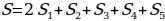 (формула 7), где
(формула 7), где
S1-площадь трапеции;
S2, S3, S4, S5-площадь оснований трапеции.
Площадь шара: 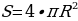 (формула 8), где
(формула 8), где
π - число «пи», = 3,1415;
r - радиус шара.
1.2 Зачем нужно измерять органы и конечности
Геометрия и ее разделы используются во всех профессиях. Она не обошла стороной и медицину. Большое значение математика имеет в таких медицинских профессиях как врач-статистик, офтальмолог, генетик и т.д. В этих профессиях нужно производить различные расчеты.
Зачем же нужно измерять органы или конечности? Измерение конечностей, внутренних органов и тела нужно, чтобы:
Изготовить протез поврежденных конечностей или внутренних органов.
Например, инженеры разработали электронные протезы конечностей, а кардиохирурги могут проводить операции по замене сердечных клапанов протезами и давно занимаются созданием искусственного сердца;
Выявить повреждения или болезни, такие как поликистоз почек (увеличение почек и кист), переломы, вывихи, растяжения (деформация).
Практическую значимость имеет расчет веса, объема, площади органов и конечностей. Например, врачи комбустиологи, лечащие ожоги, на основе площади поверхности конечностей при обширных ожогах дают прогнозы и выбирают тактику лечения.
Глава 2. Практические расчеты объема и веса руки
Я приведу несколько примеров измерения, которые потом сравню с фактическими данными из медицинских справочников, полученными статистическими методами обработки практических данных. Для этого я решу более сложную задачу: рассчитаю объем руки, от плеча до пальцев.
Вычисление веса руки
Представим руку в виде нескольких объемных геометрических фигур: цилиндров, усеченного конуса, и объемной трапеции «рисунок 6».
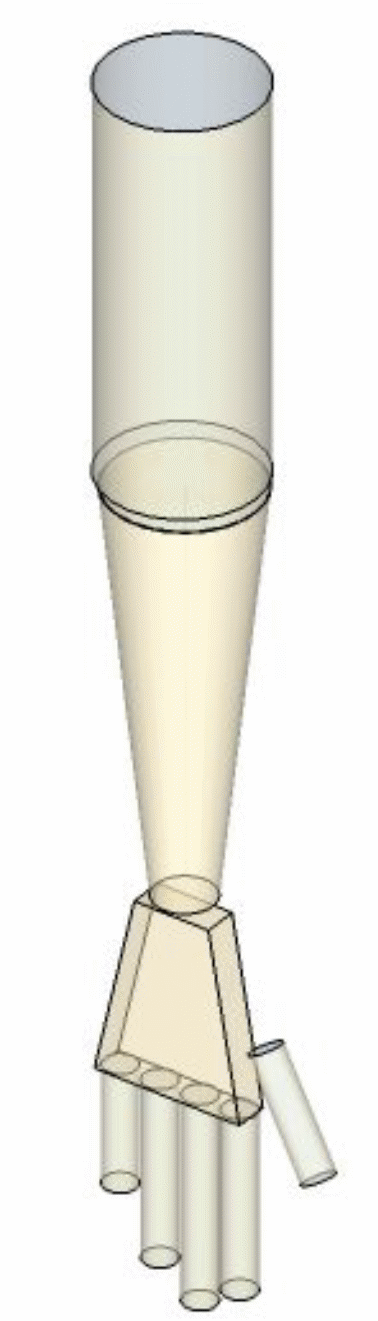
Рисунок 6 – Рука в виде объемных геометрических фигур
Средние размеры этих фигур я с помощью линейки измерю у своей руки «рисунок 7» и занесу в таблицу 1:

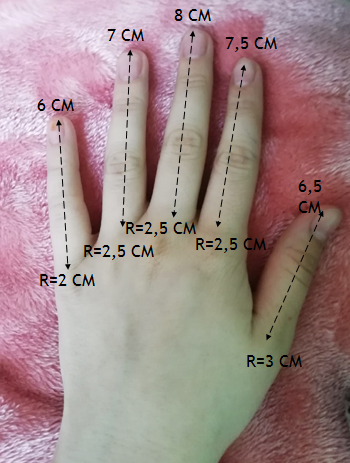
Рисунок 7 – Измерения руки
Таблица 1 – Размеры моей руки.
| Название части руки | Фигура | Размеры, мм |
| Большой палец | Цилиндр | Радиус = 30 Высота = 65 |
| Указательный палец | Цилиндр | Радиус =25 Высота = 7,5 |
| Средний палец | Цилиндр | Радиус = 25 Высота =80 |
| Безымянный палец | Цилиндр | Радиус = 25 Высота = 70 |
| Мизинец | Цилиндр | Радиус = 20 Высота = 60 |
| Ладонь | Объемная трапеция | Длина малого основания = 70 Длина большого основания = 85 Высота = 80 Толщина = 20 |
| Предплечье | Усеченный конус | Радиус малого основания = 70 Радиус большого основания = 130 Высота = 220 |
| Плечо | Цилиндр | Радиус = 180 Высота = 300 |
Объем цилиндра находится по формуле 4.
Объем усеченного конуса находится по формуле 2.
Объем трапеции находится по формуле 3.
Рассчитываю по формулам объемы и заношу полученные значения в таблицу:
Таблица 2 – Вычисленные объемы руки
|
| Название части руки | Объем, см³ |
|
| Большой палец | 21,7 |
|
| Указательный палец | 21,2 |
|
| Средний палец | 21,4 |
|
| Безымянный палец | 21,2 |
| Мизинец | 9,5 |
| Ладонь | 160 |
| Предплечье | 672,5 |
| Плечо | 711,8 |
| Общий объем: | 1639,3 |
При средней плотности человеческого тела 1,07 г/см³ моя рука весит 1кг 639 г. Проверим теоретическую массу руки. Кандидат биологических наук, профессор. В.Н. Силуянов, установил, что массы сегментов тела можно определить с помощью следующего уравнения:
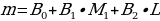 , (формула 9) где:
, (формула 9) где:
m — масса одного из сегментов тела (кг), например стопы, голени, бедра и т. д.; M1 — масса всего тела (кг), 50;
L — рост (см), 160;
В0, В1, В2 — коэффициенты уравнения, они различны для разных сегментов.
Таблица 3 – Таблица профессора В.Н. Силуянова
| Сегмент | B0 | B1 | B2 | Масса расчетная, кг |
| Кисть | - 0,116 | 0,0017 | 0,002 | 0,289 |
| Предплечье | 0,295 | 0,009 | 0,0003 | 0,793 |
| Плечо | 0,206 | 0,0053 | 0,0066 | 1,056 |
| Итого: | 2,138 |
Отклонение результатов, рассчитанных по объемным фигурам от результатов, рассчитанных по усредненным эмпирическим формулам, составило 23%, что является довольно значительным отклонением. Данное отклонение можно объяснить неточностью измерений, приблизительностью выбора геометрических форм для частей руки, а также неточностью в результатах, получаемых при расчетах эмпирических формул. Однако стоит отметить, что полученный результат может быть использован в наглядных целях, а также как доказательство того, что результаты, полученные с помощью совершенно различных методов (геометрический и биологический) примерно соответствуют друг другу.
Вычисление площади руки
В медицине, кроме объема, часто используется площадь геометрических фигур, например, врачами – комбустиологами. Для вычисления площади своей руки я воспользовалась следующими формулами:
Площадь цилиндра (формула 5).
Площадь усеченного конуса (формула 6)
Площадь объёмной трапеции (формула 7)
Далее произвела соответствующие расчеты, и данные внесла в таблицы 4 и 5.
Таблица 4 – Расчет площади руки
| Название части руки | Фигура | Размеры, мм |
| Большой палец | Цилиндр | Радиус = 30 Высота = 65 |
| Указательный палец | Цилиндр | Радиус =25 Высота = 7,5 |
| Средний палец | Цилиндр | Радиус = 25 Высота =80 |
| Безымянный палец | Цилиндр | Радиус = 25 Высота = 70 |
| Мизинец | Цилиндр | Радиус = 20 Высота = 60 |
| Ладонь | Объемная трапеция | Длина малого основания = 70 Длина большого основания = 85 Высота = 80 Толщина = 25 |
| Предплечье | Усеченный конус | Радиус малого основания = 70 Радиус большого основания = 130 Высота = 220 |
| Плечо | Цилиндр | Радиус = 180 Высота = 300 |
Таблица 5 – Площади частей руки и общая площадь
| Название части руки | Площадь, см2 |
| Большой палец | 60,44 |
| Указательный палец | 29,77 |
| Средний палец | 35,18 |
| Безымянный палец | 30,15 |
| Мизинец | 17,9 |
| Ладонь | 146,9 |
| Предплечье | 438,5 |
| Плечо | 445,8 |
| Общая площадь: | 1204,6 |
По данным таблицы 6 из медицинского справочника можно рассчитать площадь моей руки, согласно следующим данным:
Таблица 6 – Данные из медицинского справочника
| Возраст, годы | Площадь поверхности всего тела, см2 | Процент от общей площади поверхности тела % |
| Конечности | Голова | Туловище |
| Верхние | нижние |
| 8 | 10 750 | 10,0 | 33,3 | 19,5 | 37,2 |
| 12 | 11425 | 9,6 | 33,0 | 19,7 | 37,6 |
| 13 | 13 325 | 8,8 | 31,9 | 21,4 | 37,9 |
| 15 | 14 300 | 8,4 | 31,6 | 21,5 | 38,5 |
Площадь моей руки должна составлять 1204,6 см2.
Таким образом, можно сделать вывод, что площадь моей руки вычисленная с помощью формул геометрии 100% совпадает с расчетами данных из медицинского справочника.
Врачи - комбустиологи вычисляют, сколько процентов от тела составляет та или иная часть тела для того, чтобы определить насколько сильно повредился человек при ожоге.
ЗАКЛЮЧЕНИЕ
С помощью достаточно простых методов измерения и расчёта я получила конкретные параметры веса и объема взятых для примера собственной руки. Полученные результаты приблизительно соответствуют тем результатам, на которые ориентируются медики при лечении пациентов, что доказывает практическую ценность использованных геометрических методов.
Конечно, взаимодействие медицины и геометрии не ограничивается расчетом параметров органов и конечностей. Геометрия в медицине решает значительно более сложные задачи.
В медицине применяются геометрические модели различных частей скелета (например, движущейся челюсти при протезировании зубов, коленных и локтевых суставов и др.). Развитие современных 3D технологий сделало возможным создание индивидуальных протезов костей, созданных по результатам 3D - сканирования пациента. Также большую роль в современной медицине играют компьютерные модели отдельных органов и их систем. Например, при разработке серьезных операций на сердце часто используется его геометрическая компьютерная модель.
Я поняла, что такая наука как геометрия является неотъемлемой частью медицины, оказывается, на геометрии построено множество медицинских профессий, где используется современная техника. В результате своей работы мною составлена формула по нахождению площади объемной трапеции и выполнены необходимые расчеты. Я убедилась, что с помощью геометрических законов можно рассчитать конкретные параметры органа или части тела с допустимой точностью.
Таким образом, поставленная цель и задачи достигнуты в моей работе, а гипотеза доказана.
СПИСОК источников
Атанасян, Л. С. Геометрия, 10 – 11: учеб. для общеобразоват.учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др. – Москва : Просвещение, 2016. – 256 с. – Текст : непосредственный.
Мордкович, А. Г. Математика 11 класс : учебник / А. Г. Мордкович, И. М. Смирнова, П. В. Семенов, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина. – Москва : Мнемозина, 2017. – 416 с. : ил. – Текст : непосредственный.
Зациорский, В. М., Биомеханика двигательного аппарата человека : учебник / В. М. Зациорский , А. С. Аруин, В. Н. Селуянов – Москва : Физкультура и спорт, 1981. - 143с. – Текст : непосредственный.
Гилярова, М. Г. Математика для медицинских колледжей: учебник / М. Г. Гилярова. –. Ростов н/Д : Феникс, 2016. – 442, с.: ил. – (Среднее медицинское образование). Текст : непосредственный.
Тела вращения – URL : http://wikipedia.org (дата обращения 25.03.2021). – Текст : электронный.
Тела вращения – URL : http://yandex.ru/images/(дата обращения 15.02.2021). – Текст : электронный.








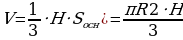 (формула 1), где
(формула 1), где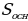 – площадь основания конуса.
– площадь основания конуса.
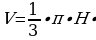 (R2 +R∙r+r2) (формула 2), где:
(R2 +R∙r+r2) (формула 2), где: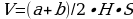 , (формула 3) где:
, (формула 3) где:
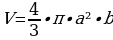 , (формула 3) где:
, (формула 3) где:
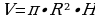 , (формула 4), где:
, (формула 4), где:
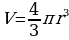 (формула 8), где
(формула 8), где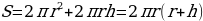 , (формула 5), где
, (формула 5), где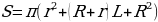 (формула 6), где:
(формула 6), где: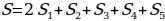 (формула 7), где
(формула 7), где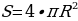 (формула 8), где
(формула 8), где


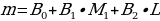 , (формула 9) где:
, (формула 9) где:









