Министерство здравоохранения Кузбасса
Новокузнецкий филиал
Государственного бюджетного образовательного учреждения
«Кузбасский медицинский колледж»
Специальность 34.02.01
Сестринское дело
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
По дисциплине
«Математика»
По теме
«Функции вокруг нас»
Обучающийся _____________ Полякова Садафмо Миноджиддиновна
(подпись) (ФИО)
Преподаватель ____________ Шилепина Надежда Ивановна
(подпись) (ФИО)
Индивидуальный проект защищен:
«___» ______________2020г.
Оценка____________________
НОВОКУЗНЕЦК 2021
ОЛГЛАВЛЕНИЕ
ВВЕДЕНИЕ 3
Глава 1. Теоретические аспекты функции 5
1.1 Что такое функция 5
1.2 Способы задания функции 6
Глава2. Практическое применение функций 10
2.1 Функции в различных науках 10
2.2 Функции в народной мудрости 14
2.3 Моделирование биологических процессов 15
ЗАКЛЮЧЕНИЕ 17
Список источников 18
Приложения 19
ВВЕДЕНИЕ
При рассмотрении количественных соотношений реального мира функции имеют большое значение, так как мы сталкиваемся с численными значениями различных физических величин, например времени, температуры, объема, длины, давления, плотности и другое. Функции позволяют воспринимать зависимость различных величин как живой, изменяющийся процесс, стараясь разглядеть самые существенные их черты, самые глубокие закономерности.
Функции стали неотъемлемой частью нашей жизни. Все явления и процессы в окружающем мире не могут быть изучены без математического описания. Реальные процессы связаны с большим количеством переменных и зависимостей между ними. Описать их можно с помощью функций и их свойств, предсказать ход их развития, управляя ими.
Еще в школе мы познакомились с различными функциями, их свойствами и графиками, но мы мало знаем о том, где в реальной жизни можно встретиться с ними, и как человек использует свойства функций в своей практической деятельности.
Актуальность проекта: Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими.
Цель исследования:
Найти и показать, где в обычной жизни вы можете встретить функции.
Задачи проекта:
Определить «Что такое функция?».
Найти и рассмотреть функции, которые существуют в нашем мире;
Проанализировать каждый способ.
Выявить, где встречаются функции в повседневной жизни.
Объект проекта: математические функции.
Предмет проекта: функциональные зависимости и встреча функций в обычной жизни.
Методы исследования: классификация, обобщение, описание и анализ.
Гипотеза проекта: функциональные зависимости существуют во всех сферах жизни человека.
Объем и структура индивидуального проекта: композиционный состав – введение, 2 главы, заключение, 9 использованных информационных источников, 1 таблица, 15 рисунков, 2 приложения.
Период исследования:
Выбор темы – октябрь;
Составление графика этапов – ноябрь;
Представление итога работы – апрель;
Сбор материала – ноября – январь;
Работа над поставленными целями, задачами. Создание доклада и презентации – ноябрь-март;
Подведение итогов, формулирование выводов, оформление презентации – март;
Подготовка к выступлению с докладом – март
Глава 1. Теоретические аспекты функции
1.1 Что такое функция
Современная математика знает множество функций, и у каждой своей неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на земле.
Мы тоже являемся функцией многих переменных, одна из которых – время. Проходят годы и мы меняемся.
В зависимости от условий величины могут принимать постоянные и переменные значения. Основным понятием математического анализа является функция. Но для понимания давайте определим, что такое функции.
Функция - правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной из множества Y.
Есть независимая переменная, которая может менять своё значение, и зависимая от неё переменная. Некоторые зависимости одной переменной от другой называют функциональными.
Функция показывает зависимость одной переменной от другой. Другими словами, взаимосвязь между величинами. Переменная y называется функцией (зависимая переменная) от другой переменной x (независимая переменная), если каждому значению x из некоторого множества ставится в соответствие одно или несколько значений переменной y. Функция записывается в виде y=f(x), х – независимая переменная, или аргумент, y – зависимая переменная, или функция, а f – это правило, по которой задается данная функция.
Функция считается заданной, если задано множество значений, принимаемых независимой переменной, и задано правило, устанавливающее соответствие между значениями аргумента и зависимой переменной.
Точно так же облик каждой функции можно представить сложенным из набора характерных деталей. В них проявляются основные свойства функций.
Наиболее часто используются следующие способы задания функции: табличный, графический, аналитический и словесный.
Эти четыре способы задания функции подробно рассмотрим далее.
1.2 Способы задания функции
Табличный способ (заключается в задании таблицы отдельных значений аргумента и соответствующим им значений функции).
Преимущество:
Для каждого значения независимой переменной, помещенного в таблице, можно сразу без всяких вычислений найти соответствующее значение функции.
Недостатки:
Обычно невозможно задать функцию полностью, найдутся такие значения независимой переменной, которые не помещены в таблице;
Отсутствие наглядности при большом объеме таблицы, трудно выявить характер изменения функции.
Примеры:
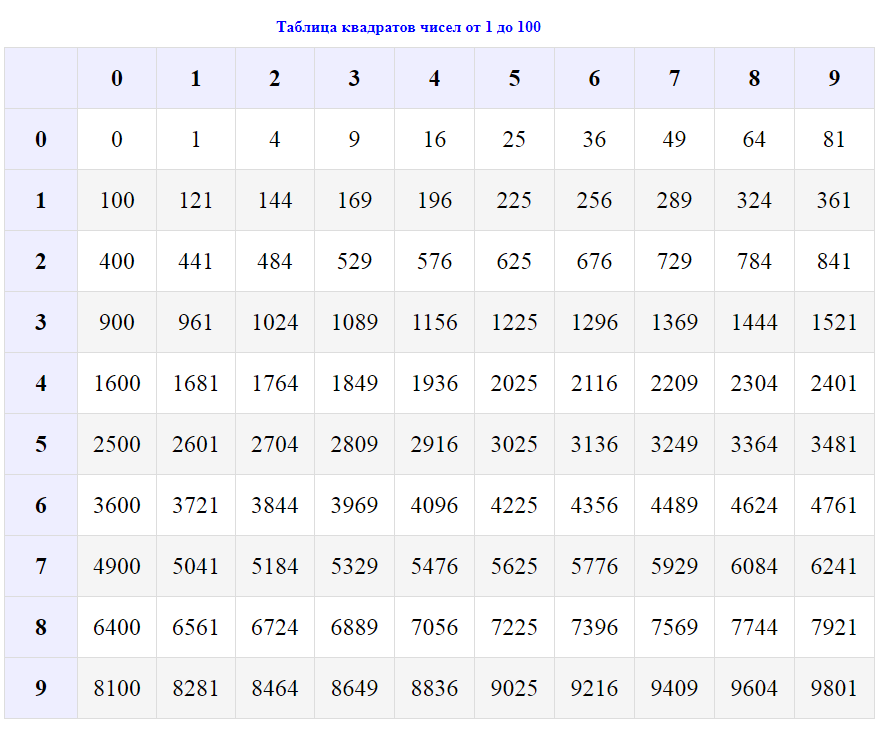
Таблица 1 – Таблица квадратов (Приложение 1)
Таблица 2 – Кубы чисел
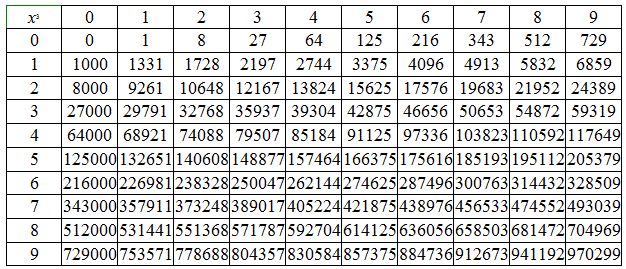
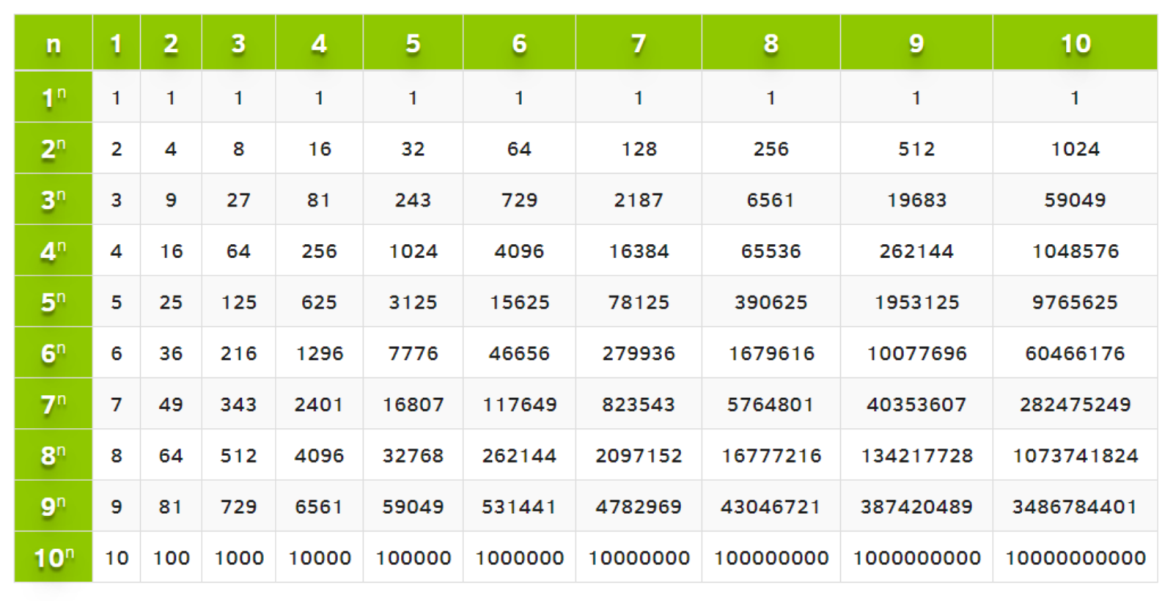
Таблица 3 – Таблица степеней (Приложение 2)
Графический способ – способ, представляющий запись изменения различных величин «рисунки 1, 2»(графиком функции у=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению).
Преимущества:
Наглядность.
Единственный способ задания для некоторых функций.
Недостаток:
Не может быть непосредственно применен аппарат математического анализа.
Примеры:
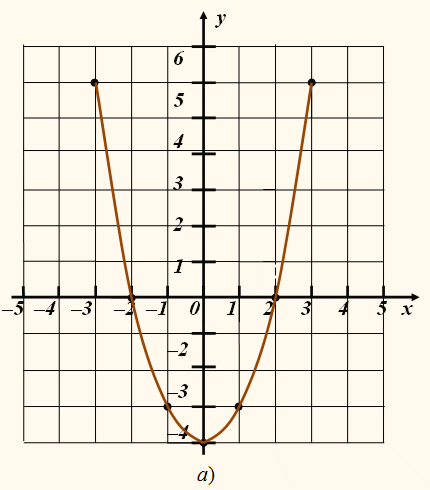
Рисунок 1 – Квадратичная функция (график – парабола)
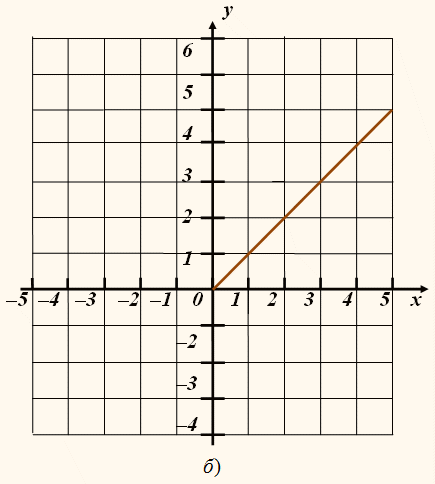
Рисунок 2 – Линейная функция (график – прямая)
Аналитический способ (закон, устанавливающий связь между аргументом и функцией, задаётся посредством формул).
Преимущества:
Сжатость, компактность задания;
Возможность вычислить значение функции для любого значения независимой переменной из области определения;
Возможность применить к данной функции аппарат математического анализа, так как он наилучшим способом приспособлен как раз к аналитической форме задания функций.
Недостатки:
Недостаточная наглядность.
Необходимость вычислений, нередко очень громоздких.
Графическое задание.
Примеры:
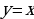 ;
;
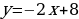 ;
;
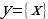 .
.
Следует отметить, что аналитическим заданием функции указывается и область определения. Если область определения не задана, то определяется значения аргумента, при которых данная функция имеет смысл.
Словесный способ (функциональная зависимость выражается словами).
Преимущество:
Возможность задания тех функций, которые не удается выразить аналитически.
Недостаток:
Невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности.
Примеры:
Меньше слов, больше дела;
Чем дальше в лес, тем больше дров;
Больше народу, меньше кислорода;
Когда делаешь варенье соотношение должно быть 1 к 2;
Глава2. Практическое применение функций
2.1 Функции в различных науках
Функция встречается в различных науках. Рассмотрим некоторые из них (медицина, физика, экономика и география).
Физика (массой тела, плотности вещества, графики радиоволн и другое) «рисунок 3».
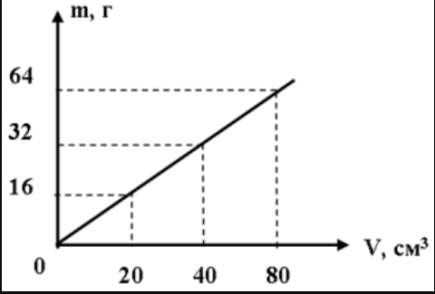
Рисунок 3 – Масса тела, плотность вещества (функция - линейная; график – прямая) «рисунок 4»
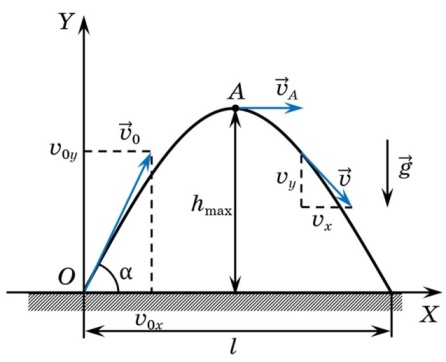
Рисунок 4 – Камень, брошенный под углом
Экономика функция потребительского спроса «рисунок 5».
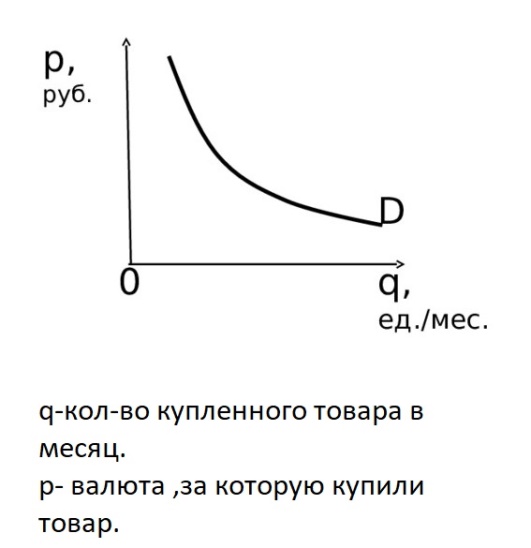
Рисунок 5 – Зависимость валюты от кол-ва купленного товара (функция - обратная пропорциональность; график - кусочная гипербола)
География которая следует из графика «рисунок 6».
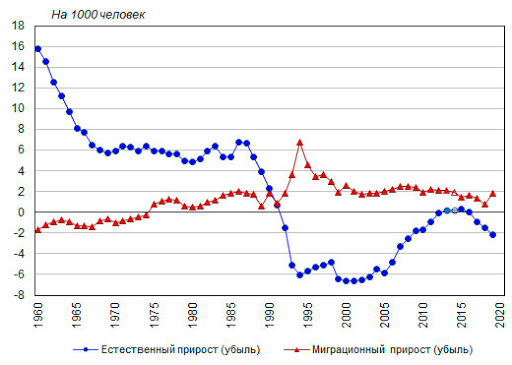
Рисунок 6 – Естественный прирост населения
Медицина, где используется большое количество различных электрограмм, которые отражают изменение во времени электрических процессов живого организма.
Давайте рассмотрим больше примеров в области медицины.
Примеры:
Электрокардиограмма - это кривая, которая отражает биоэлектрическую работоспособность сердца.
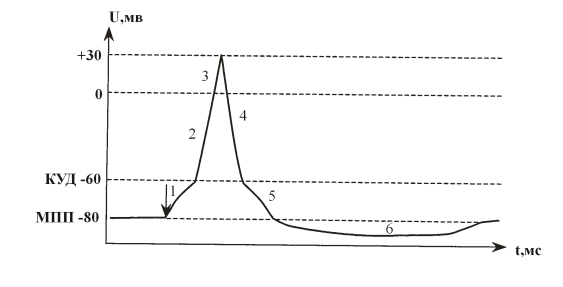
Рисунок 7 – График биоэлектрической работоспособности сердца
Трепетания желудочков является экстремальной, критической ситуацией для пациента, требующей немедленного врачебного вмешательства. Нередко это состояние критической смерти.
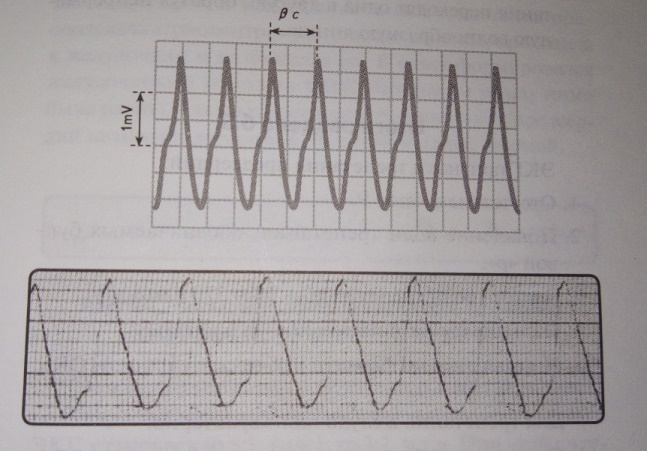
Рисунок 8 – Трепетание желудочков
Фибрилляция предсердий бывает крупно- и мелковолновой в зависимости от амплитуды f-воли. Мелковолновая фибрилляция протекает с большой частотой (около 600 в минуту) и амплитуда воли не более 0,1 mV. При крупноволновой частота импульсов составляет 450 в минуту, а амплитуда воли – около 0,2 mV.
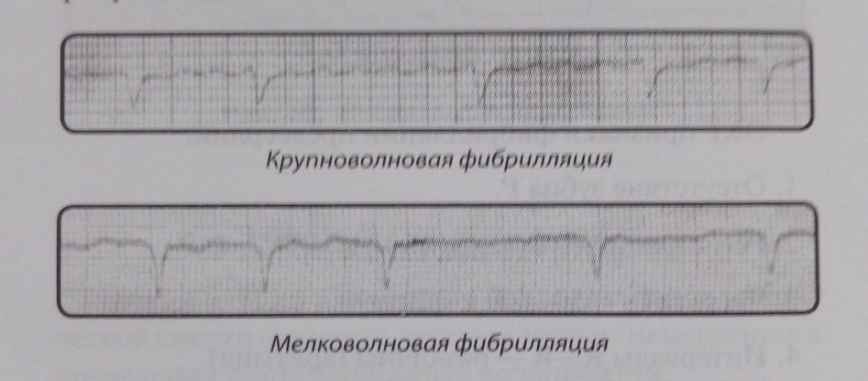
Рисунок 9 – Крупноволновая и мелковолновая фибрилляция предсердий с аритмической деятельностью желудочков
Ряд исследователей выделяют в развитии инфаркта миокарда острейшую стадию, считая ее временным интервалом от 1–3 минут до 1–3 часов.
В связи с редкими случаями регистрации ЭКГ в эти сроки развития инфаркта миокарда нет единого мнения об электрокардиографических критериях, но считается, что первыми вовлекаются в процесс субэндокардиальные слои.
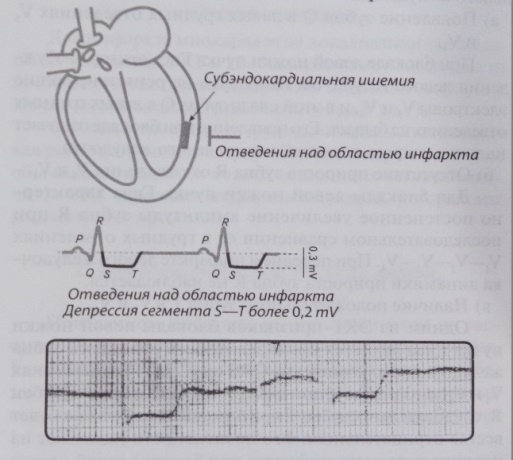
Рисунок 10 – Схематическое изображение острейшей стадии инфаркта миокарда
На рисунке 11 приведен пример использования длительного ЭКГ-мониторирования по Холтеру для диагностики различных нарушений ритма больного ИБС. Показан график изменений частоты сердечных сокращений, зарегистрированной в течение суток (рисунок 11, а). Хорошо видны два относительно непродолжительных эпизода повышения ЧСС до 160 и 150 ударов в мин, сопровождавшиеся ощущением сердцебиения.
На рисунке 11, б представлена ЭКГ, зарегистрированная во время одного из таких эпизодов, характер изменения которой позволил диагностировать наличие у больного пароксизмальной мерцательной тахиаритмии.
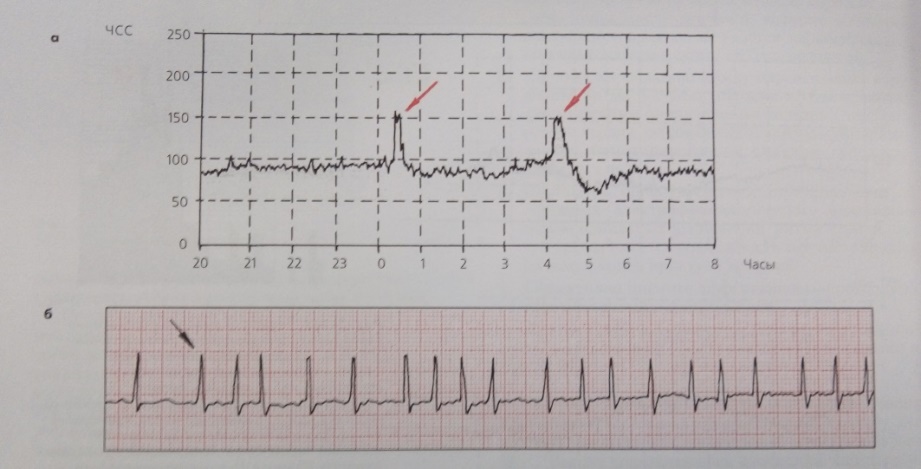
Рисунок 11 – График изменений ЧСС (а) и фрагмент ЭКГ (б),
2.2 Функции в народной мудрости
Пословицы и поговорки:
Кто много знает, с того много и спрашивается «рисунок 12».
Рисунок 12 – График поговорки
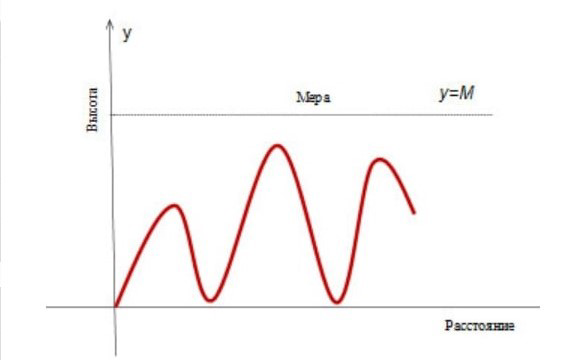
Рисунок 13 – График пословицы

Рисунок 14 – График пословицы
2.3 Моделирование биологических процессов
С помощью графика функции я рассчитала биоритмы своего состояния по дате рождения на один месяц вперед, с целью дальнейшего анализа модели.
Цель моделирования – на основе анализа индивидуальных биоритмов прогнозировать неблагоприятные дни, выбирать благоприятные дни для разного рода деятельности.
За точку отсчета я взяла дату своего рождения и рассчитала физический, эмоциональный и интеллектуальный циклы биоритмов.
Физический биоритм (ФИЗ) характеризует жизненные силы человека, т. е. его самочувствие. Периодичность данного цикла составляет 23 дня.
Эмоциональный биоритм (ЭМО) характеризует внутренний настрой человека, его способность эмоционального восприятия окружающего. Продолжительность периода эмоционального цикла равна 28 дням.
И третий биоритм характеризует мыслительные способности, интеллектуальное (ИНТ) состояние человека. Цикличность его – 33 дня.
Указанные циклы я рассчитала с помощью следующих функций:
ФИЗ: 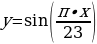 , где х – количество прожитых человеком дней;
, где х – количество прожитых человеком дней;
ЭМО: 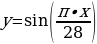 , где х – количество прожитых человеком дней;
, где х – количество прожитых человеком дней;
ИНТ: 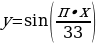 , где х – количество прожитых человеком дней.
, где х – количество прожитых человеком дней.
В результате проделанной работы я получила вот такой график функции «рисунок 15»:
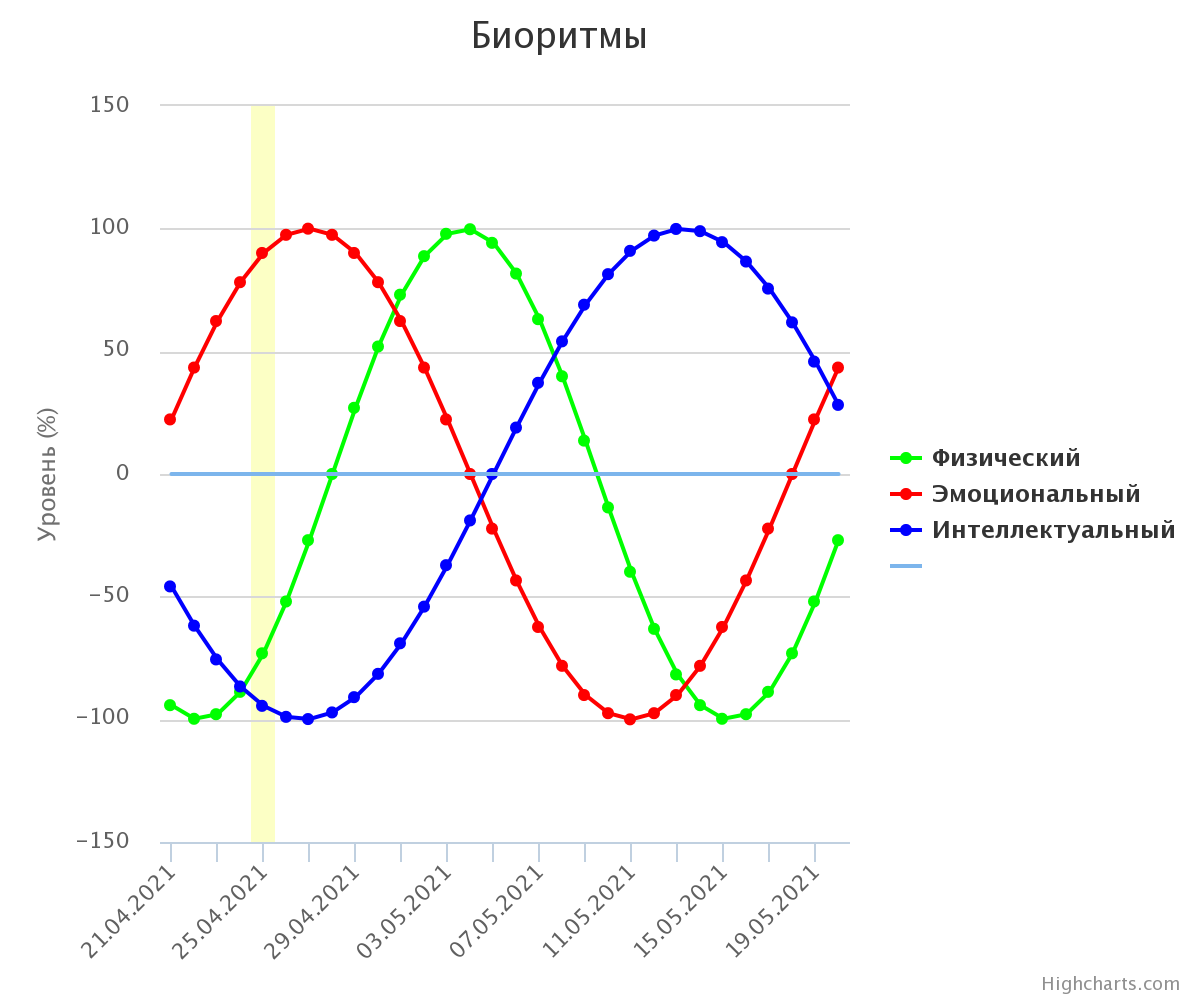
Рисунок 15 – Биоритм. Дата рождения 30.03.2004, дата отсчета 21.04.2021
ЗАКЛЮЧЕНИЕ
Функция - это из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами.
Мы стали замечать, что функции встречаются и вокруг нас. Этот интерес привел нас к небольшим исследованиям в области физики, медицины, экономике, географии.
Графики и функции широко распространены в нашей жизни, так как они содержательные, наглядные и удобны для передачи и восприятия информации, дальнейшей обработки информации (например, прогнозирование, анализ).
В рамках одной работы невозможно рассмотреть все многообразие окружающих нас функций. Я считаю, что мне удалось показать некоторые примеры нестандартного взгляда на применение математических понятий и функций в окружающей нас жизни.
В изученной теме и в соответствии с поставленными и задачами мне удалось:
Определить «Что такое функция?»;
Найти и рассмотреть функции, которые существуют в нашем мире;
Проанализировать каждый способ;
Выявить, где встречаются функции в повседневной жизни.
Таким образом, с помощью данного проекта, мне удалось узнать и показать вам, где в своей обычной жизни вы можете встретить функции.
Список источников
2. Мордкович, А. Г. Математика 10-11 класс : учебник / А. Г. Мордкович, И. М. Смирнова, П. В. Семенов, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина. – Москва : Мнемозина, 2017. – 416 с. : ил. – Текст : непосредственный.образование).
Гилярова, М. Г. Математика для медицинских колледжей: учебник / М. Г. Гилярова. –. Ростов н/Д : Феникс, 2016. – 442, с.: ил. – (Среднее медицинское образование). Текст : непосредственный.
Функции вокруг нас – URL: https://school-science.ru/7/7/39558 (дата обращения : 01.12.2020).– Текст : электронный.
Функция, производная, графики : сайт. – 2014 – . – URL: http://helpmatan.ru/page101.php (дата обращения : 01.12.2020). – Режим доступа: для авторизованных пользователей. – Текст : электронный.
Функции в повседневной жизни . – URL: https://en.ppt-online.org/599757 (дата обращения : 01.12.2020).– Текст : электронный.
Фукции . – URL: http://iamruss.ru/russian-proverbs-and-sayings/ (дата обращения : 01.12.2020). – Текст : электронный.
Понятие функции . – URL: https://foxford.ru/wiki/matematika/ponyatie-funkcii-i-sposoby-ee-zadaniya (дата обращения : 14.12.2020). – Текст : электронный.
Таблица квадратов . – URL: https://ru.onlinemschool.com/math/formula/square_table/ (дата обращения : 14.12.2020).– Изображение : электронное.
Таблица кубов. – URL: https://otvet.mail.ru/question/197444927 (дата обращения : 14.12.2020). – Изображение : электронное.
Приложения
Приложение 1
Таблица 1 – Таблица квадратов
Приложение 2
Таблица 2 – Таблица степеней









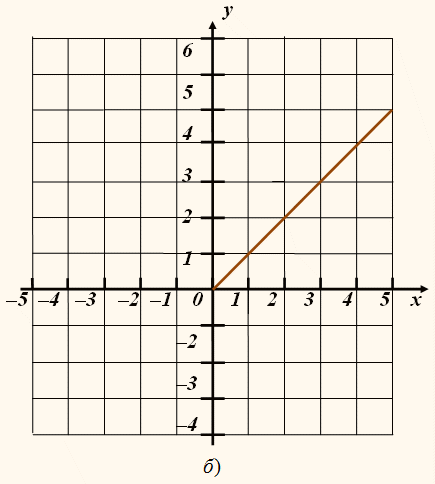
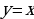 ;
;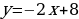 ;
;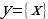 .
.











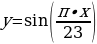 , где х – количество прожитых человеком дней;
, где х – количество прожитых человеком дней;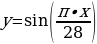 , где х – количество прожитых человеком дней;
, где х – количество прожитых человеком дней;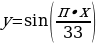 , где х – количество прожитых человеком дней.
, где х – количество прожитых человеком дней.












