Число:
Тема урока: Иррациональные уравнения
Тип урока: урок ознакомления с новым материалом
Цель урока: ввести понятие иррационального уравнения, показать способы решения иррациональных уравнений.
Учебно-воспитательные задачи урока:
Образовательные
Формирование умения и навыков решения иррациональных уравнений.
Контроль уровня усвоения знаний и умений решения уравнений, определения ОДЗ, вычислительных навыков.
Развивающие
Развитие умений выделять главное, существенное в изученном материале
Формирований умений пользоваться алгоритмом решения уравнений
Воспитательные
воспитания интереса к предмету
воспитание ответственного отношения к своему образованию.
Средства обучения: индивидуальные конспекты, записи на доске, учебник «Алгебра и начала математического анализа» 10-11 Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин. М.: Просвещение, 2014.
План урока
| № | Этапы урока | время | Методы и методические приемы |
| 1 | Орг.момент | 1 мин | Словесный(приветствие) |
| 2 | Сообщение темы и целей урока | 1 мин | Словесный, практический |
| 3 | Изложение нового материала | 15 мин | Словесный, практический |
| 4 | Закрепление материала | 20 мин | Практический |
| 5 | Подведение итогов. Домашнее задание. Рефлексия | 3 мин | Словесный (запись на доске), оценивание |
8. Ход урока
I. Организационный момент.
II. Сообщение темы и целей урока.
III. Объяснение нового материала.
Уравнение, в котором неизвестное находится под знаком корня называется иррациональным.
Алгоритм решения любого иррационального уравнения:
1) Найти ОДЗ. Корни нечетной степени в ОДЗ не нуждаются
2) Решить уравнение путём возведения обеих частей уравнения в натуральную степень
3) Сделать письменно проверку, исключить посторонний ответ
При решении иррациональных уравнений с квадратными корнями отрицательное значение квадратного корня считается невозможным и рассматривают только арифметическое значение корня, то есть положительное значение корня  =2.
=2.
Учитель разбирает задания различного уровня сложности:
1)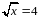 ; 2)
; 2) 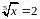 ; 3)
; 3)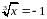 ; 4)
; 4)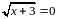 ; 5)
; 5)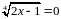 ;
;
6) 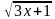 -
-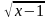 = 2
= 2
О.Д.З. 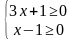
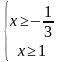 хϵ
хϵ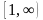
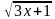 =
=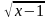 + 2
+ 2
3х+1 = х-1 +4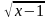 + 4 возвели обе части уравнения в квадрат
+ 4 возвели обе части уравнения в квадрат
2х-2= 4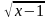
х-1 = 2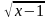 возвели обе части уравнения в квадрат
возвели обе части уравнения в квадрат 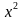 - 2х+1 = 4х-4 ;
- 2х+1 = 4х-4 ;
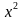 - 6х + 5 = 0
- 6х + 5 = 0
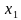 = 1
= 1 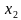 = 5 сверяем с ОДЗ
= 5 сверяем с ОДЗ
IV. Закрепление материала
Работа по учебнику: №№ 152 (1,3),153 (1,3), 154 (1,3).
Решение примеров у доски
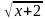 +
+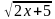 = 1
= 1
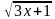 -
-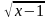 = 2
= 2
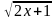 +
+ = 2
= 2 
 -
- =
= 
V. Подведение итогов. Рефлексия.
В о п р о с ы у ч а щ и м с я:
– Какие уравнения называются иррациональными?
– Опишите алгоритм решения иррациональных уравнений.
Домашнее задание: №№ 152 (2),153 (2), 154 (2,4).
2







 =2.
=2. 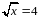 ; 2)
; 2) 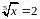 ; 3)
; 3)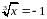 ; 4)
; 4)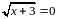 ; 5)
; 5)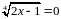 ;
;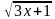 -
-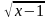 = 2
= 2 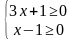
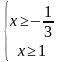 хϵ
хϵ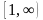
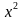 - 2х+1 = 4х-4 ;
- 2х+1 = 4х-4 ; 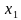 = 1
= 1 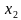 = 5 сверяем с ОДЗ
= 5 сверяем с ОДЗ 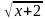 +
+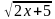 = 1
= 1 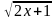 +
+









