ИСПОЛЬЗОВАНИЕ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ ПРИ ОБУЧЕНИИ МАТЕМАТИКИ В УЧРЕЖДЕНИИ СПО

ГБПОУ «Агротехнический техникум» с.Дивное

ИСПОЛЬЗОВАНИЕ ПРАКТИКО-ОРИЕНТИРОВАННЫХ ЗАДАЧ

ПРИ ОБУЧЕНИИ МАТЕМАТИКИ В УЧРЕЖДЕНИИ СПО

Выполнила: Волобуева Светлана Яковлевна

Оглавление

Введение……………………………………………………………………….. 3

Глава 1. Теоретические вопросы темы

1.1. Задачный подход в практике преподавания математики……………….. 6

1.2. Роль практических задач при обучении математики ……………………12

Глава 2. Практико-ориентированные задачи при обучении математики в учреждении СПО.

2.1. Построения методики практико - ориентированных задач……………19

2.2. Разработка и анализ практико-ориентированных задач………………25

Заключение……………………………………………………………………34

Список литературы…………………………………………………………..36

Приложения……………………………………………………………………39

Введение

В век технологий система образования ставит своей главной целью подготовку для общества квалифицированных специалистов. Математика всегда была неотъемлемой частью всей истории человеческой культуры; она является ключом к познанию окружающего на мира, базой научно-технического прогресса и важной компонентой развития личности. Все математические знания и навыки необходимы практически во всех профессиях, прежде всего в тех, которых связаны с естественными науками, техникой, экономикой. Но математика стала проникать и в области традиционно «нематематические» - управление государством, медицину, лингвистику и другие. Несомненна необходимость применения математических знаний и математического мышления врачу, историку, лингвисту, но и также важно математическое образование для профессиональной деятельности служащих и рабочих.

Результаты государственной итоговой аттестации учащихся 9-х и 11-х классов свидетельствуют о низком уровне сформированности умений использовать математические знания и методы для решения практико-ориентированных задач. Очевидно, что такие результаты являются следствием недостаточного внимания к обучению школьников практико-ориентированным задачам в силу некоторых причин. Этот фактор обуславливает актуальность исследования. Так как будущие специалисты, изучая специальные предметы, постоянно сталкиваются с потребностью в тех или иных математических знаниях. Поэтому математику следует рассматривать как важнейшую составляющую качественной подготовки специалистов. Это обусловлено не только тем, что математика является важным элементом общей культуры, универсальным языком науки, в целом, но и, главным образом, тем, что она является мощным средством решения прикладных и практико-ориентированных задач. В учебное заведение СПО отделения начальной профессиональной подготовки приходят учащиеся с низкой математической подготовкой, но у многих из них интересы в определенной степени уже сформированы: они направлены на избранную профессию. Поэтому одним из мотивов, стимулирующих интерес к изучению того или иного вопроса курса математики, является его практическая и профессиональная значимость. А этого можно добиться, используя практико-ориентированные задачи при обучении, но действующие учебники мало предлагают таких задач.

Цель работы: разработать методические рекомендации по применению практико-ориентированных задач в процессе изучения курса математики на 1 курсах.

Объект работы: Процесс изучения математики в СПО.

Предмет работы: Практико-ориентированные задачи в курсе математики.

Предметом исследования выступают организационные особенности в работе преподавателя общеобразовательного учреждения.

Гипотезой исследования является предположение о том, что применение практико-ориентированных задач при обучении математике в условиях общеобразовательного учреждения будет эффективной, если:

• в работе будут использованы личностно-ориентированные, групповые, коллективные, коррекционные, интегративные и интерактивные технологии;

• ориентация коррекции будет осуществляться не на отдельные свойства личности, а на целостную систему значимых знаний обучающихся;

• коррекционная работа будет построена с учётом возраста, то есть в процессе коррекции должна осуществляться деятельность, которая позволит раскрыться наиболее актуальным потребностям возраста.

В соответствии с целью нашего исследования были выделены следующие задачи:

1. На основе анализа педагогической и методической литературы уточнить понятие практико-ориентированной задачи, охарактеризовать требования к ним и рассмотреть методические условия применения;

2. Определить роль и место практико – ориентированных задач в учебном процессе;

3. Проверить эффективность применения задач на практике.

4. Рассмотреть практико-ориентированные задачи в курсе математики и уровни сложности практико-ориентированных задач;

5. Организовать, провести и проанализировать экспериментальное исследование по данной проблеме.

Организация и этапы исследования. Исследование проводилось в период с 2015 по 2016 уч. годы и состояло из следующих этапов:

- подготовительный этап включал в себя определение концептуального замысла исследования, определение цели, формулирование задач, изучение научной литературы по проблеме;

- констатирующий этап связан с выбором методов и методик научного исследования, а также проведением первичной диагностики;

- контрольно-диагностический этап включал в себя обработку и анализ экспериментальных данных, оформление курсовой работы.

База исследования: ГБПОУ «Агротехнический техникум» с. Дивное. Выборка составила 50 испытуемых.

Структура работы: работа состоит из введения, двух глав, заключения, библиографического списка и приложения.

Глава 1.Теоретические вопросы темы

В этой главе рассмотрено определение практико-ориентированной задачи, цель их использования, виды. Какие задачи относят к практико-ориентированным. Рассмотрены требования, предъявленные к практико-ориентированным задачам, примеры, в которых отражена трактовка этих требований. Сформулированы методические условия применения практико-ориентированных задач в курсе математики. Распределение задач по уровням сложности. Определение уровней сложности по критериям.

1.1.Задачный подход в практике преподавания математики

Для человека чрезвычайно важно не столько энциклопедическая грамотность, сколько способность применять обобщённые знания и умения для разрешения конкретных ситуаций и проблем, возникающих в реальной действительности. По мнению психологов В. В. Давыдова и методистов - математиков Д. Пойа, Л. М. Фридмана, Г. И. Саранцева, Т. А. Ивановой, формировать способность разрешения проблем помогают специальным образом подобранные задачи. Будем называть их практико-ориентированными.

Практико - ориентированная задача – это вид сюжетных задач, требующий в своем решении реализации всех этапов метода математического моделирования.

Рассмотрим понятие «задача» в педагогической литературе. В широком смысле задача рассматривается как проблемная ситуация с явно заданной целью, которую необходимо достичь. В более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать. Т.Ф. Ефремова [12] под задачей предлагает считать цель, к которой стремятся, которую хотят достичь, обстоятельства, затруднения, которые надо преодолеть. Под математической задачей она понимает вопрос математического характера, требующий нахождения решения по известным данным с соблюдением определённых условий. В словаре Ожегова определение задачи звучит следующим образом: «Задача – упражнение, которое выполняется посредством умозаключения, вычисления»[28].

Д. Пойа, рассматривая роль задач в математике, писал: «Что значит владение математикой? Это есть умение решать задачи, причём не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности»[32].

Наиболее распространённым является определение задачи как системы (Г.А. Балл, Ю.М. Колягин, Л.М. Фридман, А.Ф. Есаулов) [3], [17],[44].

Одним из моментов в модернизации современного математического образования является усиление прикладной направленности курса математики, то есть осуществление связи его содержания и методики обучения с практикой. Проблема прикладной направленности обучения математике не нова и на всех этапах её становления и развития была связана с множеством вопросов, часть из которых не решена до сих пор. Проблема прикладной направленности математики динамична по своему содержанию и в силу постоянного развития математической теории, прогресса ЭВМ, расширения области человеческой деятельности. Даже будучи однажды решённой, она с каждым новым витком истории будет требовать переосмысления и корректировки. Об этом нужно не забывать. Научно-техническая революция во всех областях человеческой деятельности предъявляет новые требования к знаниям, технической культуре, общему и прикладному характеру образования. Это ставит перед современным образованием новые задачи совершенствования образования и подготовки специалистов к практической деятельности.

Авторы по-разному очерчивают круг явлений, относящихся к объёму понятия «задача». Термин «задача» употребляют для обозначения объектов, относящихся к трём различным категориям:

1. к категории словесной формулировки этой ситуации (Л.М. Фридман, А.А. Столяр и др.)[39];

2. к категории цели действий субъекта, требования, поставленного перед субъектом (А.Н. Леонтьев, В.Н. Пушкин и др.)[18];

3. к категории ситуации, включающей наряду с целью условия, в которых она должна быть достигнута (Г.А. Балл, Л.Л. Гурова, Ю.М. Колягин, Ю.Н. Кулюткин, П.М. Эрдниев, А.Ф. Эсаулов и др.)[13].

Такие задачи называют по-разному: компетентностные, контекстные, ситуационные, сюжетные, практико-направленные, компетентностно-ориентированные, учебно-практические позволяющие проверять уровень сформированности различных компетенций. В нашем исследовании мы будем их называть «практико-ориентированные задач», учитывая их целевое назначение в процессе обучения.

Прикладная и практическая направленность обучения – одна из содержательно - дидактических линий, тесно связанная с другими линиями курса математики.

Прикладная направленность обучения математике предполагает ориентацию его содержания и методов на тесную связь с жизнью, основами других наук, на подготовку обучающихся к использованию математических знаний в предстоящей профессиональной деятельности, на широкое применение в процессе обучения современной электронно-вычислительной техники.

Практическая направленность обучения математике предусматривает ориентацию его содержания и методов на изучение математической теории в процессе решения задач, на формирование у обучающихся прочных навыков самостоятельной деятельности, связанных, в частности, с выполнением тождественных преобразований, вычислений, измерений, графических работ, использованием справочной литературы, на воспитание устойчивого интереса к предмету, привитие универсально - трудовых навыков планирования и рационализации своей деятельности.

Прикладная и практическая направленность неразрывны, переплетаются в реальном учебно-воспитательном процессе. Практика показывает, что обучающиеся с интересом решают и воспринимают задачи практического содержания. Обучающиеся с увлечением наблюдают, как из практической задачи возникает теоретическая, и как чисто теоретической задаче можно придать практическую форму.

Однако в учебниках математики таких задач почти нет. В методических пособиях практико-ориентированные задачи встречаются редко. Подбор задач, формирующих элементарные навыки приложения математики, дело не простое. Многие из текстовых задач в учебниках неестественны с прикладных позиций. Поиск и систематизация поучительных и в то же время достаточно простых задач подобного рода – весьма актуальная проблема.

Часто у обучающихся возникает мысль, будто бы задачи бывают прикладные, т.е. нужные в жизни, и не практические, которые в жизни не понадобятся. Для устранения таких ошибок целесообразно использовать любую возможность показа того, что абстрактная задача может быть связана с прикладными. Решение практико - ориентированных задач, тогда эффективно, когда обучающиеся встречались с описываемой ситуацией в реальной действительности: в быту, на экскурсии, при изучении других предметов. Эффективным средством является широкое использование наглядности: фотографий, слайдов, плакатов, рисунков и т.д.

Такие задачи повышают интерес обучающихся к самому предмету, поскольку для подавляющего большинства ценность математического образования состоит в её практических возможностях.

Под задачей с практическим содержанием понимается математическая задача, содержание которой раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит ее с использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций. Содержание таких задач, представленных в учебнике, может быть дополнено задачами на:

• вычисление значений величин, встречающихся в практической деятельности;

• построение простейших номограмм;

• составление расчётных таблиц;

• вывод формул зависимостей, встречающихся на практике.

Важным средством достижения прикладной и практической направленности обучения математике служит планомерное развитие у обучающихся наиболее ценных для повседневной деятельности навыков выполнения вычислений и измерений, построения и чтения графиков, составления и применения таблиц, пользование справочной литературой. Возможны различные пути формирования подобных навыков. В этой связи являются перспективными вычислительные практикумы, лабораторные работы по измерению геометрических величин, измерительные работы на местности, задания на конструирование и преобразование графиков.

Задачи с практическим содержанием целесообразно использовать в процессе обучения для раскрытия многообразия применения математики в жизни, своеобразия отражения ею реального мира и достижения дидактических целей таких, как:

• мотивация введения новых математических понятий и методов;

• иллюстрация учебного материала;

• закрепление и углубление знаний по предмету;

• формирование практических умений и навыков.

Дидактическими целями практико-ориентированных заданий являются:

• закрепление и углубление теоретических знаний;

• овладение умениями и навыками по учебной дисциплине;

• формирование новых умений и навыков;

• приближение учебного процесса к реальным жизненным условиям;

• изучение новых методов научных исследований;

• овладение обще учебными умениями и навыками;

• развитие инициативы и самостоятельности.

Виды практико-ориентированных заданий:

• Аналитические (определение и анализ цели, выбор и анализ условий и способов решения, средств достижения цели);

• Организационно-подготовительные (планирование и организация практико-ориентированной работы, индивидуальной, групповой или коллективной по созданию объектов, анализ и исследование свойств объектов труда, формирование понятий и установление взаимодействий между ними);

• Оценочно-коррекционные (формирование действий оценки и коррекции процесса и результатов деятельности, поиск способов совершенствования, анализ деятельности) [13]. Таким образом, практико-ориентированные задания способствуют ознакомлению учащихся с разнообразным математическим материалом, имеющим прикладной характер и развивающим творческие способности и познавательные интересы учащихся.

1.2. Роль практических задач при обучении математики

Подбор задач для создания образовательных продуктов обеспечит достижение максимального обучающего, развивающего и воспитательного эффекта при использовании таких продуктов в преподавании математики в средних профессиональных образовательных учреждениях. Часто уроки математики не дают убедительного ответа на вопрос «зачем все это нужно?» Здесь должна решаться важная методическая проблема сближения методов решения задач с методами, применяемыми на практике; необходимо раскрытие особенностей прикладной математики, её воспитательных функций; усиливать межпредметные связи. Необходимо на доступном для обучающихся языке обеспечивать действительные взаимосвязи содержания математики с окружающим миром, рекомендовать применение отдельных тем в смежных науках, в профессиональной деятельности, в производстве, в быту.

Роль и значение математики в развитии межпредметных связей и формировании у обучающихся навыков практической деятельности рассматриваются в работах М.Б. Балка, Б.В. Гнеденко, В.А. Гусева, А.Г. Мордковича, А.В. Усовой и других. Анализ работ перечисленных авторов позволяет сделать вывод о том, что эта связь осуществляется за счёт прикладной направленности математики. При этом основным носителем такой направленности являются практико-ориентированные задачи (Е.В. Величко, И.М. Шапиро и др.). Именно поэтому межпредметные связи являются важным условием и результатом комплексного подхода в обучении обучающихся.

Объект математики – весь мир, и его изучают все остальные науки. Привлечение межпредметных связей повышает научность обучения, доступность (теория насыщается практическим содержанием), естественным образом проникают на урок элементы занимательности. Однако появляется и немало трудностей: преподавателю требуется освоить другие предметы, практическая задача обычно требует больше времени, чем теоретическая, возникают вопросы увязки программ и другие.

Для формирования интереса  к изучению предмета  следует создавать  производственные проблемные ситуации, которые решаются при помощи математических знаний и умений. Изучение сложного математического материала становится  более интересным,  если обучающиеся видят практическое применение изучаемых тем непосредственно в своей профессиональной деятельности.

 Решение задач с производственной направленностью способствует формированию у обучающихся способностей находить в профессиональной ситуации существенные признаки математического понятия, подводить объект под  математическое понятие, использовать его в новых условиях.       В процессе решения  предусматривается совершенствование рационального  применения теоретических знаний к решению практических задач, развития пространственного воображения и вычислительных навыков учащихся,  организации  самостоятельной работы с измерительными приборами, таблицами, справочной литературой. Видение возможности реализации приобретаемых знаний способствует развитию мотивации к обучению и достижению успеха. Таким образом, решение задач профессионального характера на уроках способствует развитию интереса к математике как к науке и как к профессионально значимой дисциплине, показывает прикладной, реально ощутимый характер математики. Обучающиеся понимают, что математика – важный предмет в их образовании. Любая конструкция, любой технологический процесс требует расчетов, порой содержащих больше математики, чем техники.

По утверждению Н.А. Терешина, одна из функций практико-ориентированных задач состоит в том, чтобы дать учащимся представление о возможностях использования математики для решения проблем, поставленных другими областями знаний [41]. Такая задача носит не только дидактический характер, в ней соединена достоверность описываемой ситуации и доступность её разрешения, средствами школьного курса математики. Практико-ориентированная задача – это, прежде всего, учебная задача и, она способствует обучению математике, приобретению знаний именно в этой области. Важным этапом решения практико-ориентированной задачи является её перевод на язык математики. Для этого необходимо понимание нематематической ситуации, описанной в её сюжетной основе, обучающиеся могут опираться только на уже имеющиеся у них знания и жизненный опыт. Если таковые отсутствуют или недостаточны, то решение и математической части задачи становится трудным для подростков. Немаловажным является и то, что сама постановка задачи должна быть интересна для обучающегося. Интерес этот может состоять в получении новой, значимой для него информации об окружающем мире, в возможности проверить на практике результат задачи или в объяснении математической природы явлений, которым он может быть свидетелем в реальной жизни.

В работе В.А. Петрова [30] сформулированы следующие требования к задачам:

1. Производственная реальность сюжета.

2. Математическая существенность сюжета.

3. Естественность вопроса задачи.

4. Математическая содержательность.

5. Терминологический лаконизм.

Некоторые из рассмотренных требований уже не отвечают современному образованию. Так, например, требованию краткости и простоты анализа сюжетного содержания или требованию терминологического лаконизма не соответствуют контекстные задачи, которые носят практико-ориентированный характер и обладают довольно сложным и обширным сюжетным содержанием, требующим тщательного анализа условия для построения математической модели. Задачи практико-ориентированные могут быть использованы на всех этапах обучения, а не только после решения достаточного числа стандартных математических задач по изучаемой теме [13].

Основываясь на анализе такого типа задач в обучении и обобщая выделенные другими авторами требования, формируется ряд требований, разделяющий их на требования к сюжету содержания и требования к математическому содержанию задачи.

I. Требования к сюжетному содержанию задачи.

1.1. Отражение в тексте задачи реального объекта, его свойств.

1.2. Демонстрация в содержании сюжета задачи связи математики с другими науками, практическими областями деятельности.

1.3. Наличие в тексте задачи проблемы или свойств объекта, для изучения которых необходимо применить математику.

1.4. Соответствие сюжетного содержания возрастным особенностям (познавательным интересам) школьника.

1.5. Доступность содержания сюжета для понимания учащимся: используемые нематематические термины известны школьникам в результате изучения других дисциплин, легко определяемы или интуитивно ясны.

II. Требования к математическому содержанию задачи.

2.1. Математическая содержательность решения задачи.

2.2. Соответствие численных данных задачи реальным значениям.

2.3. Соответствие фактических данных реальному процессу, объекту, ситуации, описанных в задаче.

2.4. Единство задач, применяемых в преподавании математики [13].

В методической литературе выделены три направления использования практико-ориентированных задач на уроке математики:

1) задачи или практические задания для введения новых понятий и теорем;

2) несложные задачи для первичного закрепления введенных понятий и теорем;

3) более сложные задачи для включения понятия в систему известных фактов. Такие задачи решаются учащимися в классе и дома, которые применяются с дальнейшей целью закрепления изученного материала, формирования математических умений.

Задачи последней группы также могут быть включены в различные итоговые и проверочные работы. Во внеурочное время задачи включались в содержание факультативных, кружковых занятий по математике [15].

Итак, перечень требований к математическому содержанию практико-ориентированных задач позволяет отбирать задачи этого типа из различных источников, переформулировать их согласно заданным требованиям.

В настоящее время предлагается включать практико-ориентированные задачи в содержание обучения. Они представлены в форме наиболее близкой к той, в которой такие задачи имеют место в реальности или в соответствующей области знаний. Конечно, для их решения на уроке требуется значительное время, которое не всегда возможно выделить. Однако появившиеся в настоящее время разнообразные формы внеурочной работы (проектная и исследовательская деятельность, курсы по выбору) позволяют решить эту проблему.

Рядом авторов выделены принципы построения моделей, их типы, требования к математической модели [20], [26], [35], [42]. Анализ результатов этих исследований позволил резюмировать ряд особенностей метода математического моделирования.

1. Математика применяется не к реальному объекту, а к его содержательной модели.

2. У одного объекта может быть несколько математических моделей. Создаваемая модель должна отражать те свойства реального объекта, которые входят в проблему его исследования. Для исследования реального объекта могут быть использованы математические модели различных типов. Для исследования различных объектов может быть использована одна модель. (Принцип множественности моделей)

3. Соответствие математической модели реальному объекту относительно и имеет рамки применимости. (Требование адекватности модели реальному объекту)

4. Если выбранные математические средства позволяют провести исследование реального объекта в приемлемые сроки и экономно по затратам труда и средств, то выбранная модель является достаточно простой. (Требование достаточной простоты)

5. Модель должна давать возможность с помощью математических методов получить необходимую информацию о реальном объекте. (Свойство полноты математической модели)

6. В большинстве случаев сложный объект, возможно, расчленить на ряд агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными стандартные, хорошо изученные математические модели. (Принцип агрегирования)

7. Оценка результатов исследования математической модели происходит по следующим направлениям: верификация (проверка адекватности результата поставленной задаче); оценка точности и единственности полученных результатов [13].

Это, хотя и схематичное, описание особенностей математического моделирования даёт представление о способе его применения для «математического понимания природы» [19], о направлениях формирования способности к такой деятельности.

Таким образом, представления о математическом моделировании имеют общекультурную и общеобразовательную ценность и составляют математическую культуру каждого – и обучающегося, и преподавателя. Подтверждением этому мнению служат исследования многих учёных: математиков, методистов, педагогов, психологов.

Представления о модели, математической модели, методе математического моделирования, его этапах, особенностях, принципах построения математических моделей составляют методологическую основу обучения обучающихся практическим приложениям математики [13].

Выполнение описанных выше условий позволит более эффективно применять практико-ориентированные задачи в процессе обучения обучающихся общеобразовательных учреждений математике.

Глава 2. Практико-ориентированные задачи при обучении математики в учреждении СПО.

В данной главе описаны методические особенности обучению решения практико-ориентированных задач, выделены умения в процессе практико-ориентированного обучения. Рассмотрено значение математического моделирования в практико-ориентированном обучении математике. Представлены конспекты уроков ознакомления с новым материалом с применением практико-ориентированных задач.

2.1. Построения методики применения практико-ориентированных задач

Профессионально значимые знания и умения являются основой построения методики применения практико-ориентированных задач. Задачи с профессиональной направленностью создаются на основе тех знаний и умений по математике, которые непосредственно или опосредованно связаны с профессиональными знаниями и умениями. В учебном заведении за ними закрепилось название профессионально значимых. Одним из главных условий построения методики применения задач по математике с профессиональной направленностью является отбор совокупности этих знаний и умений.

Целесообразность выделения такой линии как практико-ориентированные задачи следует из современных целей математического образования, отражённых в соответствующих нормативных документах, и назревшей потребности систематизировать такие приложения, определить цели и результаты их изучения. Методологическая (Методология — учение о методах, способах и стратегиях исследования предмета.) функция линии практико-ориентированных задач состоит в изучении понятий и методов, объединяющих содержание не только методических, но и предметных линий всего школьного курса математики. К её базовому понятию естественно отнести понятие математической модели, т. к. оно проявляется во всех средствах обучения приложениям математики в техникумах, колледжах. Математическим методом выделяемой линии является метод математического моделирования [13], [28].

Решение задач профессионального отбора следует начинать с понимания того, какие именно требования предъявляются к человеку данной профессии, какими видами деятельности ему предстоит овладеть.

Профессионально значимые знания и умения по математике могут применяться в «готовом виде» для формирования на их основе профессиональных умений и навыков, теоретического обоснования практических действий и т.д. Эти знания помогают осмыслить сущность той или иной производственной операции; понять принципы устройства и действия орудий труда, справедливость требования безопасности труда.

Рассмотрим пример таких математических знаний, которые после введения их в курс математики могут быть использованы для теоретического обоснования некоторых производственных операций. Так, знание соответствующих аксиом и теорем стереометрии обосновывает правильность способов выполнения действий мастера отделочных строительных работ при провешивании поверхностей и придает осмысленность работе с отвесом, уровнем и правилом.

В качестве характерных признаков профессионально значимых математических знаний и умений можно принять следующие: соответствие отбираемых знаний и умений целям математической подготовки; связь математических знаний и умений с содержанием профессиональной подготовки; отражение отбираемыми знаниями и умениями тенденций развития отраслей народного хозяйства.

Существуют профессионально значимые математические знания, которые первоначально вводятся, а затем формируются не только на уроках математики, но и на уроках других предметов естественно - математического цикла (физике, географии и т.д.). Они служат для лучшего осознания обучающимися производственных процессов, операций, для повышения их профессиональной грамотности.

Ряд профессионально значимых знаний и умений могут первоначально формироваться на предметах профессионально-технического цикла, затем обогащаться и уточняться на уроках математики. Профессионально значимые математические знания и умения могут первоначально вводится на уроках математики, а формироваться и применяться на уроках математики, профессиональных дисциплинах и производственном обучении.

Таким образом, применение задач с профессиональной направленностью требует выявления признаков профессионально значимых знаний и умений, а также отбора (согласно этим признакам и требованиям к отбору) совокупности знаний и умений из курса математики, значимых для данной профессии. Установление этапов межпредметного и межциклового формирования выделенных знаний подтвердило положение о необходимости соблюдения преемственности в процессе их изучения и обозначило место введения дидактических материалов с профессиональной направленностью в структуре урока, а именно при актуализации основных знаний и умений, формировании и закреплении новых понятий и способов действий.

Урок – основная форма организации обучения в современном образовании. Различают несколько основных типов урока: урок усвоения новых знаний, урок комплексного применения знаний и умений (закрепления), урок актуализации знаний и умений (повторения), урок систематизации и обобщения знаний и умений, урок контроля знаний и умений, урок коррекции знаний, умений и навыков, комбинированный. Особую роль в организации процесса обучения, в том числе и обучения вопросам планиметрии отводят урокам ознакомления с новым материалом, это обусловлено целевыми установками уроков такого типа. [53]

Урок ознакомления обучающихся с новым материалом или сообщения (изучения) новых знаний - это урок, содержанием которого является новый, неизвестный учащимся материал. На таких уроках в зависимости от их содержания, конкретной дидактической цели и подготовленности, обучающихся к самостоятельной работе в одних случаях преподаватель сам излагает новый материал, в других — проводится самостоятельная работа обучающихся под руководством преподавателя, в-третьих — практикуется и то, и другое.

Структура урока ознакомления с новым материалом определяется его основной дидактической целью: введением понятия, установлением свойств изучаемых объектов, построением правил, алгоритмов и т.д. Его основными этапами являются [43]:

1) сообщение темы, целей, задач урока и мотивации учебной деятельности;

2) подготовка к изучению нового материала через повторение и актуализацию опорных знаний;

3) ознакомление с новым материалом;

4) первичное осмысление и закрепление связей и отношений в объектах изучения;

5) постановка задания на дом;

6) подведение итогов урока.

В силу своего содержания, практико-ориентированные задачи на уроке рассматриваемого типа могут служить средством для создания условий, обеспечивающих формирование у первокурсников мотивации к изучению нового материала. Поскольку они могут в ходе решения данных задач применить знания и навыки из повседневной жизни, а также проверить свой результат на практике.

На таких уроках целесообразно предлагать обучающимся для решения практико-ориентированные задачи, для решения которых им необходимо получить новые знания, овладеть новыми умениями. Решение самой задачи происходит непосредственно после изучения нового материала, который будет служить инструментом для её решения.

Для примера приведём конспект урока на которых обучающиеся работают с практико-ориентированными задачами.

Конспект урока

Тема занятия Обобщающий урок по теме Тела вращения. Решение задач.

Тип урока закрепления знаний и умений.

Цели:

Образовательные- применение теоретических знания при решении задач с практическим содержанием; применение математических знаний в реальной жизни.

Развивающие - развитие логического мышления, пространственного воображения;

-совершенствование, развитие, углубление знаний учащихся по теме;

-развитие мыслительной деятельности;

- развивать умение работы в команде;

Воспитательная - воспитывать потребность в знаниях;

-аккуратность и точность в расчетах;

-воспитание стремления к самореализации.

Оборудование-набор моделей геометрических тел;

- компьютер, презентации, задания для каждой группы;

- кроссворд.

Межпредметные связи сельское хозяйство, строительство, окружающий мир.

ХОД УРОКА

I (3 мин) Организационный момент: -приветствие

-проверка наличия учащихся

- сообщение темы и цели урока

II Актуализация опорных знаний:

А закрепление теоретического материала по телам вращения. Учащиеся рассказывают о цилиндре, конусе, шаре с помощью созданных заранее презентаций.(15 мин)

( 50мин ) Б Для решения задач практической направленности, в которых необходимо знания теоретического материала по телам вращения, используется групповой метод. Группа делится на 3 подгруппы. Каждая получает свое задание. Учитель в группе назначает консультанта - сильного учащегося. Если при выполнении задания возникают трудности, консультирует учитель. Когда задания выполнены, от каждой подгруппы один ученик защищает решение. Оценка ставится общая.

Цилиндр

1. При постройке водопровода длиной 1 метр были использованы трубы диаметром 60сантиметров. Определите объем земли, подлежащей вывозу.

1. Определите вместимость зернового элеватора, имеющего 40 резервуаров. Размеры резервуаров: высота 30м, диаметр 10м. Объемная масса зерна 0,8т.

1. Для хранения нефтепродуктов в сельском хозяйстве часто используют горизонтальные цилиндрические резервуары диаметром 3250мм и длиной 8983мм. Какова номинальная емкость резервуара? Сколько алюминиевой пудры необходимо для его покраски, если на 100м² поверхности требуется 5кг?

Конус

1. Коническая куча зерна имеет высоту 2,4м, а окружность основания 20 метров. Сколько тонн зерна в куче, если масса 1м равна 750кг?

1. Щебень укладывается в кучу, имеющую форму конуса с углом откоса 30. Какой высоты должна быть куча, чтобы ее объем был равен 10м³ ? .

1. Сосуд имеет вид усеченного конуса, высота которого 27см и длины окружностей оснований равны 66см и 96см. Сколько литров вмещает сосуд?

Шар

1 Внутренний диаметр чугунного полого шара равен 8см, а его внешний диаметр 10см. Определите массу шара, если плотность чугуна равен7,3г/см³.

1. Сколько кожи потребуется для изготовления покрышки футбольного мяча диаметром 20см, если на обрезки и швы идет 8% материала?

3 В каком случае расходуется больше материала: на никелировку одного шара диаметром 8см или на никелировку 10 шаров диаметром по 2см каждый?

III От каждой группы учащийся записывает решение на доске. Остальные учащиеся в это время решают кроссворд.

IV Защита решения каждой подгруппой.

V (10 мин )Решение кроссворда по теме Тела вращения

Вопросы к кроссворду – 1

По горизонтали. 1. Фигура на плоскости, все точки которой расположены не далее данного расстояния от одной точки. 2. Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса. 3. Тело, полученное вращением прямоугольника вокруг одной из его сторон. 4. Угол между высотой и плоскостью основания конуса. 5. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его.

По вертикали. 1. Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов. 2. Плоская фигура, при вращении которой образуется усечённый конус. 3. Тело вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра. 6. Фигура, полученная вращением полуокружности вокруг её диаметра. 7. Тело вращения, об устойчивости движения которого написана известная работа великой русской женщины – математика.

Ответы к кроссворду - 1.

По горизонтали. 1. Круг. 2. Образующая. 3. Цилиндр. 4. Прямой. 5. тор.

По вертикали. 1. Конус. 2. Трапеция. 3. Купол. 4. Диаметр. 5. Шар. 6. Сфера. 7. Юла.

Вопросы к кроссворду – 2

По горизонтали. 1. Фигура, полученная вращением параболы вокруг её оси. 2. Отрезок, соединяющий центр сферы с любой её точкой. 3. Круг, являющийся элементом конуса, плоскость которого перпендикулярна оси конуса. 4. Музыкальный инструмент, часть которого напоминает Псевдосферу Лобачевского. 5. Отрезок, соединяющий две точки окружности.

По вертикали. 1. Фигура, полученная вращением гиперболы вокруг её оси. 2. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 3. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его. 4. Тело, полученное вращением полукруга вокруг его диаметра. 5. Фигура, полученная вращением полуокружности вокруг её диаметра. 6. Тело вращения, принцип движения которого описала великая русская женщина-математик. 7. Фигура, полученная вращением эллипса вокруг её оси.

Ответы к кроссворду - 2.

По горизонтали. 1. Параболоид. 2. Радиус. 3. Основание. 4. Труба. 5. Хорда.

По вертикали. 1. Гиперболоид. 2. Высота. 3. Тор. 4. Шар. 5. Сфера. 6. Юла. 7. Эллипсоид.

VI (3 мин) Итоги урока Рефлексия

1. Какие знакомые правила, теоремы были использованы на этом занятии?

2. На какие знакомые факты опирались при выполнении заданий на этом занятии?

VII Домашнее задание составить практико-ориентированную задачу по теме тела вращения.

2.2. Разработка практико-ориентированных задач

Практика показывает, что обучающиеся с интересом решают и воспринимают задачи практического содержания. Обучающиеся с увлечением наблюдают, как из практической задачи возникает теоретическая, и как чисто теоретической задаче можно придать практическую форму.

 К задаче следует предъявлять следующие требования:

• задачи должны соответствовать программе курса, вводиться в процесс обучения как необходимый компонент, служить достижению цели обучения;

• вводимые в задачу понятия, термины должны быть доступными для обучающихся, содержание и требование задачи должны «сближаться с реальной действительностью»;

• способы и методы решения задачи должны быть приближены к практическим приёмам и методам;

• прикладная часть задачи не должна покрывать её тематическую сущность;

Практико-ориентированные задачи могут быть использованы с разной дидактической целью: они могут заинтересовать или мотивировать, развивать умственную деятельность, формировать практические умения и навыки, объяснять соотношение между математикой и другими дисциплинами.

Следует различать так называемые практические задачи из учебников математики и задачи, появляющиеся перед тем или иным работником в процессе его трудовой деятельности.

В тексте задач по математике для нахождения искомой величины (например, объёма или площади) обычно приводятся все необходимые для этой цели данные, и притом ровно столько сколько нужно для получения ответа. В практико-ориентированной задаче эти данные ещё надо найти, выбрать те параметры и характеристики, значения которых требуются для вычисления искомой величины. Задачи прикладного характера отличаются некоторой неопределённостью в математическом понятии, порой необходимы дополнительные данные, а чтобы их отыскать обращаемся к источнику информации, который позволяет снять неопределённость прикладной задачи.

При решении задач по специальности задача упрощается, если обучающиеся представляют реальную ситуацию. Перевод условия практической задачи на язык математики, если, человек, решающий задачу, имел или имеет возможность увидеть данный объект в натуре, вникнуть в соответствующую производственную ситуацию, опираясь на специальную литературу, владеет необходимым математическим аппаратом.

При решении практико-ориентированных задач необходимо перейти к их математическим моделям. В простейших ситуациях такие модели тривиальны: поле-прямоугольник; бочка-цилиндр; ведро - усечённый конус; тюк сена - параллелепипед; расчётная ситуация - соответствующие ей алгебраическое уравнение. Выбор той или иной модели определяется рядом факторов: требуемой точностью измерений; здравым смыслом; опытом математизации задач.

Отыскание способа для решения реальной прикладной задачи-это только первый шаг. Затем алгоритм применяется к задаче с конкретными числовыми значениями. При численном расчёте необходимо соблюдение естественных требований здравого смысла. Например: возможно ответ записать в виде конечной десятичной дроби, полученной после округления, необходимо помнить, что значения параметров являются приближенными, и поэтому необходимо соблюдать правила приближенных вычислений.

Решение всех задач проходит в четыре эта­па.

1.Анализ условия задачи.

Задача формулиру­ется на описательном языке. От правильной постановки задачи, указания ресурсов, которыми мы располагаем, зависит успеш­ность ее решения. Этому нужно учиться каждому, так как пригодится специалисту любого профиля.

2.Построение математической модели задачи.
Перевод исходной задачи на математический язык: вводятся переменные, ищутся связи между ними и устанавливаются ограничения на них, которые записываются в виде уравнений, неравенств или их систем. Любая математическая задача - модель каких-то прикладных задач (экономических, физических, биологических, технических и т.п.).

3. Решение математической модели задачи.

Изучается полученная модель. Если задача извест­ная, то она решается по соответствующему ей алго­ритму. Если задача никогда не решалась, то ищется необходимый алгоритм.

4.Интерпретация решения. Это перевод реше­ния задачи на исходный язык.

Решение задач с практическим содержанием могут быть предложены обучающимся на различных этапах обучения. Решение задач на этапах восприятия  и осмысления нового материала имеет целью пробудить у обучающихся потребность в расширении знаний, познавательный интерес и научить их методам самостоятельного приобретения знаний. Решая и анализируя задачи на этапах закрепления и повторения учебного материала, обучающиеся овладевают способами применения знаний на практике и вместе с тем более глубоко усваивают его содержание. При проверке усвоения программного материала решение задач с производственным содержанием позволяет установить, насколько прочно и глубоко его усвоили

Рассмотрим примеры практико-ориентированных задач.

1. Рассчитайте расход масляной краски, идущей на окраску панели помещения (высота 3м, ширина 4м, длина 5м, высота панели 2,2м), если на окраску 1м² требуется 0,2 кг (окна и двери занимают 12% площади поверхности).

2. Сколько литров побелки надо налить в емкость для краскопульта диаметром 20 см и высотой 60 см.

3. Рассчитать массу стальной трубы длинной 7,5 см, зная что внешний и внутренний диаметры ее соответственно 155 и 135мм, а плотность стали равна 7960кг/м³ .

4. Сварщику необходимо изготовить бункер, имеющий форму правильной четырехугольной призмы, длина стороны основания которого равна 1,4м, а высота – 2,3м. Сколько стали необходимо для выполнения работы? ( на швы следует добавить 3% материала)

5. Рассмотрим задачу связанную с конусом. Сначала обсуждается одна из ситуаций, в которой фигурирует объект, имеющий форму конуса (это куча щебня), ищется решение проблемы измерения необходимых для решения задачи величин.

Задача. Найти объем кучи щебня.
— Будем считать, что куча щебня имеет форму конуса. Какие элементы конуса необходимо знать, чтобы вычислить искомые величины?
— Радиус основания, длину образующей и высоту конуса.
— Высоту и радиус основания невозможно найти непосредственным измерением. Как найти радиус основания в этом случае?
— Пусть у нас имеется, например, мягкая метровая лента. Измерим ею длину окружности основания кучи щебня и разделим это число на 2π.
— Каким образом можно измерить длину образующей?
— Перекинув метровую ленту через вершину кучи, мы определим длину двух образующих. Разделим ее на 2.
— Осталось определить высоту кучи щебня.
— Зная радиус и длину образующей, вычислим по теореме Пифагора высоту кучи щебня. 
— Теперь мы можем вычислить площадь поверхности и объем кучи щебня. После измерения получили: длина окружности кучи щебня равна 7,2 м. Длина двух образующих — 2,6 м. Найдите объем этой кучи, считая π = 3.
— Вычислим радиус основания конуса: 
Длина одной образующей равна 1,3 м. Высоту конуса вычислим по теореме Пифагора
Тогда 

Исследования по выявлению знаний и умений решения практико-ориентированных задач проводилось на уроках математики в группах первого курса. При изучении темы графическое исследование функций в двух группах первых курсов, имеющих одинаковый уровень знаний (по итогам входного контроля), обучающимся была предложена практико-ориентированная задача, на местном материале. Группа 115 первыми выполняла практико-ориентированную задачу, а затем упражнение из учебного пособия: Колмогоров А.Н. «Алгебра и начала анализа 10-11». А группа 114 вначале выполняла упражнение из учебного пособия: Колмогоров А.Н. «Алгебра и начала анализа 10-11», а второе упражнение практико-ориентированную задачу. Результаты выполнения работы представлены в таблицы. Анализ результатов показывает, что в группе 115 количество обучающихся выполнивших задание из учебного пособия на хорошо и отлично больше, чем в группе 114. Имеет место ситуация, что обучающиеся группы 115 проявляя, интерес к практико-ориентированной задача, да плюс на местном материале, более осознанно подошли к исследованию функции. В их работе над первым задании отсутствуют ошибки по нахождению периодов, когда среднемесячная температура воздуха больше нуля, меньше нуля. Верно, указаны и промежутки знак постоянства функции в упражнении из учебного пособия. В группе 114 имеются ошибки при нахождении промежутков знак постоянства функции в упражнении из учебного пособия, а вот в задании по нахождению периодов, когда среднемесячная температура воздуха больше нуля, меньше нуля, отсутствуют ошибки.

	Группа 115	Группа 114
Задание1	практико-ориентированная задача	упражнение из учебного пособия Колмогоров А.Н. Алгебра и начала анализа 10-11 класс
Задание2	упражнение из учебного пособия Колмогоров А.Н. Алгебра и начала анализа 10-11 класс	практико-ориентированная задача

Практико-ориентированная задача

Задача постройте график изменения среднемесячной температуры воздуха за 2015 год по данным аэрологической станции Дивное за 2015 год.

Укажите:

1Какой период по времени взят для анализа температуры; разность между наибольшей и наименьшей температурой воздуха в течение год;

2 дату перехода температуры воздуха через 0 градусов С (в сторону повышения и в сторону понижения температуры воздуха);

3 продолжительность периода среднемесячной температуры воздуха выше 10градусов С;

4 периоды, когда среднемесячная температура воздуха больше нуля,

меньше нуля;

5 периоды, в течение которых среднемесячная температура воздуха повышается, понижается;

6 дату максимальной среднемесячной температуры воздуха и её значение,

дату минимальной среднемесячной температуры воздуха и её значение.

При решении статистических задач рекомендуется использовать практико-ориентированные задачи с региональным данными.

	C средняя многолетняя	C 2015год
Январь	-5.2	-1.9
Февраль	-4.6	-0.4
Март	1.1	4.1
Апрель	9.3	10.2
Май	16.3	17.6
Июнь	21.3	24.9
Июль	23.9	26.5
Август	23.1	25.4
Сентябрь	17.0	21.2
Октябрь	10.3	8.7
Ноябрь	3.0	5.7
декабрь	-2.3	2.4
	9.5	12.0

№93а Колмогоров А.Н. Алгебра и начала анализа 10-11 класс

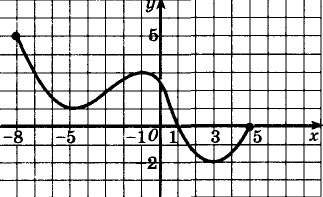
1 найдите область определения и значений данной функции;

2 выявить обладает, ли функция особенностями облегчающимися исследование: а) чётная, нечётная б) периодическая;

3 вычислить координаты точек пересечения с осями координат;

4 найти промежутки знак постоянства функции;

5 выяснить промежутки, на которых функция возрастает, убывает;

6 найти точки экстремума; вид экстремум, значение функции в этих точках.

Таблица 1. уровень знаний (по итогам входного контроля)

	Группа 115	Группа 114
Количество обучающихся	25	25
«5»	0	0
«4»	2	2
«3»	20	21
«2»	3	2
Абсолютная успеваемость	88%	92%
Средний балл	3.0	3.0
Качество знаний	8%	8%

Диагностика обученностиобучающихсягруппы 114,115(по итогам входного контроля)

Таблица 2 Результаты выполнения заданий

	Задание практико-ориентированное			Задание из учебного пособия
	номер исследу емого свойства	Количествообучающихся верно выполнив ших задание	Количествообучающихсяневерно выполнив ших задание	номер исследу емого свойства	Количествообучающихся верно выполнив ших задание	Количествообучающихсяневерно выполнив ших задание
гр у п п а 1 1 5	1	21	4	1	20	5
	2	22	3	2	19	6
	3	22	3	3	22	3
	4	22	3	4	22	3
	5	22	3	5	20	5
	6	22	3	6	20	5
г р у п п а 1 1 4	1	17	8	1	16	9
	2	18	7	2	15	10
	3	18	7	3	15	10
	4	18	7	4	14	11
	5	19	6	5	17	8
	6	19	6	6	17	8

Таблица 3

Процент обучающихся верно выполнивших задание

	Практико-ориентированное задание	Задание из учебного пособия
Группа 114	68%	56%
Группа 115	80%	68%

Диагностика обученностио бучающихся группы № 114 115

дисциплина «Математика»

 

тема: Графическое исследование функций

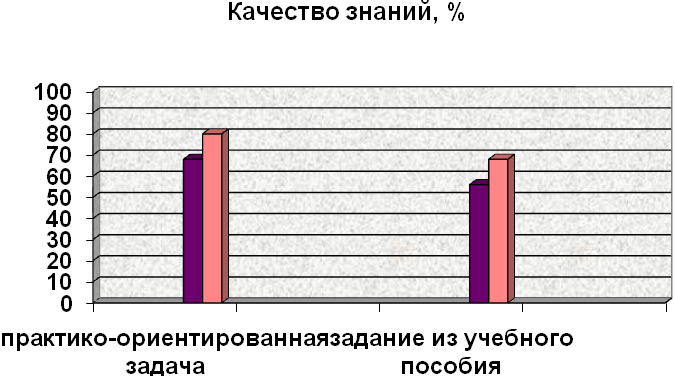
При решении статистических задач рекомендуется использовать практико-ориентированные задачи с региональными данными.

Итак, задачи с профессиональной направленностью служат средством управления познавательной деятельностью обучающихся. Они применяются на любом из этапов процесса формирования профессионально значимых математических понятий и теоретических утверждений: могут быть задействованы на уроке до, после и одновременно с введением новых знаний.

Вывод: Решение практико-ориентированных задач на уроке означает использования дополнительных возможностей изучаемого материала, адекватных способов организации изучения традиционного программного материала.

Для применения на уроке практико-ориентированных задач преподавателем могут быть использованы следующие дополнительные возможности изучаемого материала:

- прикладной характер содержания темы;

- содержание, включающее в себя оценку явлений и событий; различные концепции; различные толкования причин и следствий, другие противоречивые сведения или позиции, допускающие различное толкование;

- материал, имеющий существенное значение для местного сообщества, связанный с широко обсуждаемыми в обществе вопросами (например, проблемы экологии, вопросы межэтнических отношений и т.п.);

- содержание программы, связанное с событиями, явлениями, объектами, доступными непосредственному восприятию обучающегося (в том числе в учебных ситуациях);

- материал, работа с которым допускает выход за пределы техникума, его изучение на базе предприятий, высших учебных заведений, учреждений культуры;

- содержание учебной программы, связанное с формированием учебных умений и навыков;

- содержание учебного материала, которое может найти применение в воспитательной, досуговой, организационной и т.п. деятельности.

Развитие у обучающихся умений решать практико-ориентированные задачи в процессе обучения математике следует рассматривать как один из способов формирования у них математической компетентности. Такой подход к обучению позволяет в дальнейшем выпускнику техникума решать проблемы, возникающие в жизни и в профессиональной деятельности.

Заключение

Проанализировав методическую и педагогическую литературу, мы дали более точное понятие практико-ориентированной задачи. Охарактеризовали и обобщили имеющиеся требования к практико-ориентированным задачам: 1) требования к сюжетному содержанию задачи; 2) требования к математическому содержанию задачи.

Рассмотрели методические условия применения практико-ориентированных задач в курсе математики. В процессе исследования выявлены четыре уровня сложности задач на приложения:

1) в тексте задачи имеется прямое указание на математическую модель;

2) прямого указания на модель нет, но объекты и отношения задачи однозначно соотносимы с соответствующими математическими объектами и отношениями;

3) объекты и отношения задачи соотносимы с математическими объектами и отношениями, но неоднозначно - требуется учёт реально сложившихся условий;

4) объекты и отношения задачи явно не выделены или их математические эквиваленты неизвестны обучающимся.

Практико-ориентированное обучение направленно на развитие познавательных потребностей, функционирования мышления, организацию поиска новых знаний, повышению эффективности образовательного процесса, формирование практического опыта и использования его при решении жизненно важных задач и проблем. Для лучшего развития практико-ориентированного подхода в обучении математике является самое эффективное средство – практико - ориентированные задачи, задачи связанные с окружающей действительностью. Если в обучении использовать практико-ориентированные задания, то будет лучше усваиваться полученная информация, потому что задачи основаны на действительности, в них отражаются конкретные действия и события, что может происходить в повседневной жизни, присутствуют подлинные условия. Обучающимся на много интереснее работать с такими задачами. Они способствуют творческому развитию личности, развитию мышления, интеллектуальности, воображения.

Практика показала, что систематическая работа по решению и конструированию  практико-ориентированных задач и использование разнообразных приёмов даёт положительные результаты. Изучение сложного математического материала становится  более интересным, обучающиеся находят практическое применение изучаемых тем в своей профессиональной деятельности.

Рано или поздно всякая правильная математическая идея находила применение в том или ином дее.

Крылов А.Н.

В заданиях показывается обучающимся значимость математических знаний для их профессии, что ориентирует их на новый, более высокий  уровень изучения математики.  Систематическое использование на уроках задач профессиональной направленности является связующей нитью между теорией и практической деятельностью, что способствует более глубокому освоению профессии,  способствует развитию интереса к математике как к науке и как к профессионально значимой дисциплине, показывает прикладной, реально ощутимый характер математики. Обучающиеся понимают, что математика – важный предмет в СПО.

Методик использования практико-ориентированных задач и их составления при обучении математике разработано недостаточно. Поэтому необходимо составлять такие задачи и определять их место на уроках математики. Решение задач с практическим содержанием – одна из форм работы по осуществлению профессиональной направленности преподавания математики в средних профессиональных учреждениях.

Таким образом, все задачи решены, цель исследования достигнута.

Список литературы

1. Ахлимерзаев А. Прикладная направленность изучения начал математического анализа в старших классах средней школы как средство усиления принципов политехнизма в обучении: дис. … канд. пед. наук. Фергана, 1986.

2. Бабанский Ю.К. Развитие познавательного интереса школьников // Дополнительное образование. 2003. № 3. C. 15.

3. Балл Г.А. О психологическом содержании понятия «задача» // Вопросы психологии. 1970. № 6. С 10-15.

4. Бахвалов Н. Большойэкономическийсловарь.М.:Институтновойэкономики.А.Н.Азрилиян.1997.

5. Болтянский В.Г. Математическая культура и эстетика // Математика в школе. 1982. № 2. С. 40-43.

6. Большой энциклопедический словарь. 2-е изд. М.: Большая Российская энциклопедия, 1998. 1456 с.

7. Брадис В.М. Методика преподавания математики в средней школе. М., Гос. учебно-педагог. изд. мин. прос. РСФСР, 1954. 504 с.

8. Варданян С.С. Задачи по планиметрии с практическим содержанием: Кн. Для учащихся 6-8 кл. ср. шк. / под ред. В.А. Гусева. М.: Просвещение, 1989. 144 с.

9. Геометрия. Пробный учебник для 10-11 классов общеобразовательных учреждений / В.Н. Руденко, Г.А. Бахурин, А.Я. Цукарь. М., ИД «Искатель» 2005. 320 с.

10. Геометрия: Учеб.пособие для 11 кл. с углубл. изучением математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. М.: Просвещение, 2004. 319 с.

11. Гуткин Л.И. Сборник задач по математике с практическим содержанием. М.: Высшая школа, 1968. 112 с.

12. Ефремова Т.Ф. Новый словарь русского языка. Толково-словообразовательный. М.: Русский язык, 2000.

13. Колмогоров А.Н. Алгебра и начала математического анализа 10-11 классы М. «Просвещение» 2012/ Колмогоров А.Н.

14. Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. М.: Наука, 1990. 240 с.

15. Смирнова И.М. Педагогика геометрии. М.: Прометей, 2004. 336 с.

16. Статья по психологии [Электронный ресурс]. URL: http://o-psihologii.info/deti/ped/878-soderzhanie-obucheniya.html, (дата обращения: 24.03.2015)

17. Столяр А. А. Педагогика математики. Минск: Высшая шк., 1986.

18. Тарасов Л.В., Тарасова А.Н. Беседы о преломлении света / под ред. В.А. Фабриканта. М.: Наука. Гл. ред. физ.-мат. лит., 1982. 176 с.

19. Терешин Н.А. Прикладная направленность школьного курса математики: Кн. для учителя. М.: Просвещение, 1990. 96 с.

20. Тихонов А.Н., Костомаров Д.П. Рассказы о прикладной математике. М.: Наука, 1981. 210 с.

21. Федеральный государственный образовательный стандарт основного общего образования [Электронный ресурс]. URL: http://минобрнауки.рф/документы/938/файл/749/10.12.17-Приказ_1897.pdf (дата обращения: 17.04.2015).

22. Фридман, Л.М. Как научиться решать задачи: пособие для учащихся / Л.М. Фридман, Е.Н. Турецкий. М.: Просвещение, 1984.

23. Фридман, Л.М. Теоретические основы методики обучения математике. М.: Либроком, 2009. 248 с.

24. Хаймина Л.Э. Задачи прикладной направленности в обучении математике: учебно-методическая разработка для учителей школ и студентов математического факультета. Архангельск: Помор.гос. ун-т им. М.В. Ломоносова, 2000. 47 с.

25. Шапиро И.М. Использование задач с практическим содержанием в преподавании математики. М: Просвещение, 1990. 96 с.

26. Шевкин А.В. Как не надо обновлять тематику школьных задач // Математика в школе. 1995. №2. С.51-53.

27. Якутов М.И. Пути реализации прикладной направленности курса алгебры восьмилетней школы: дис. ... канд. пед. наук. М., 1988.

28. Кулюткин Ю.Н. Мышление и личность. СПб.: КРСМАС, 1995. 232 с.

29. Закатов П. С. Курс высшей геодезии. М.: Недра, 1976. С 8-9.

30. Герасимова Т. П., Неклюкова Н.П. Начальный курс географии. 6 класс. М.: Дрофа, 2010. 176 с.

31. Конструирование современного урока математики: кн. для учителя / С.Г. Манвелов. 2-е изд. М.: Просвещение, 2005. 175 с.

Приложение 1.

Задания для обучающихся по профессии «Мастер отделочных строительных работ»

«Многогранники »

 Задача № 1.

Здание имеет  форму прямоугольного параллелепипеда: длина 24 метра, ширина 7 метров и высота 8 метров. Определить поверхность здания без учёта крыши.

     А. Сколько необходимо затратить  кирпича на строительство,  если кладка выполнялась в два кирпича и предусмотрено 4  оконных  простенка  (1500х1700) и дверной проем (1500х2400)

(размер кирпича, мм  250х120х65, шов 1см).

       Б. Сколько необходимо сухой штукатурной смеси с теплоизоляционными и водоотталкивающими свойствами на основе цемента для оштукатуривания  фасада здания. (Расход смеси 18,5 килограмм на  один квадратный метр).

     В. Сколько кубических метров доски израсходуется на устройство дощатых полов, если  размер доски (300 х80х40)

Тема: «Объем призмы»

Задача № 2

Подсчитайте расход раствора при укладке плиток в помещении 6x4 м., если толщина стяжки 16 мм., толщина прослойки 7 мм. Сколько потребуется плиток, если размер плитки 15x15x0,5 см.?

Задача № 3.

Сколько часов потребуется маляру для окраски панели высотой 2м в помещении (высота 2,7 м, ширина 2,4 м, длина 5 м) маховой кистью или валиком, если норма времени для окраски 100 м² поверхности: кистью –6,4 часа, валиком – 3,4 часа. К данной задаче можно предложить чертеж помещения.

 Задача №4

    Рассчитать расход бетона для устройства фундамента под колонну стаканного типа высотой 0,9 метра, стороной нижнего основания 1 метр, стороной верхнего основания 0,8 метра. Колонна представляет собой правильную четырехугольную призму со стороной 0,5 метра и устанавливается в фундамент на глубину 0,5 метра.

Задача № 5.

Найдите вместимость сарая прямоугольной формы с двускатной крышей и прямым углом между стропилами.  Размеры сарая: длина – 10 метров, ширина 7 метров, высота стен до крыши 3,5 метра, высота от основания до конька крыши 8,5 метра

Задача № 6.

Постамент   для установки мемориальной плиты  имеет форму правильной усечённой пирамиды, верхняя площадка – квадрат со стороной 2 метра, сторона нижнего основания 10 метров. Определить объем  постамента, если его высота 7 метров.

        А.  Сколько необходимо кованного декоративного уголка для обрамления боковых углов постамента.

    Б. Рассчитать количество  каменной декоративной штукатурки для высококачественного оштукатуривания боковой поверхности постамента. Расход раствора для декоративной штукатурки

 0,02 м³  на один квадратный метр.

        В. Сколько плит,  размером 60х60 сантиметров,  необходимо для покрытия основания постамента (указать размеры и количество остатков плит).

        Г. Какой длины нужно порезать кованную декоративную металлическую полосу для закрепления её от углов верхнего основания  перпендикулярно рёбрам нижнего основания.

Тема: «Площадь поверхности цилиндра»

Задача № 7.

Рабочий отштукатуривает вручную колонну улучшенной штукатуркой. Сколько времени ему потребуется, чтобы отштукатурить колонну высотой 6 м., диаметром 1 м., соблюдая норму времени 0,79 ч. на 1м Ответы. 1) 14,2ч; 2) 6,1 ч; 3)0,7 ч; 4) 8,1 ч.

Задача № 8.

Рабочий отштукатуривает вручную колонну улучшенной штукатуркой. Сколько он заработает, если колонна имеет высоту 5,5 м., радиус колонны 0,5м., а норма расценки 46,6 коп. на 1 м ?

Ответы. 1) 19,1 руб.; 2) 7,7 руб.; 3) 4,2 руб.; 4) 1090 коп.

Задача № 9.

При отштукатуривании вручную колонны рабочему потребовалось 4 ч. Какую площадь поверхности он отштукатуривал за 1 ч., если высота колонны 7 м., диаметр основания 0,8 м.?

Ответы. 1) 1,2 м²; 2)14 м²; 3) 4,2 м²; 4) 5 м².

Задача № 10.

При норме времени 0,79 ч. на 1 м² рабочий вручную отштукатуривает колонну высотой 8 м. за 4,8 ч. Определите диаметр основания этой колонны. Ответы. 1) 1,2 м.; 2) 2,5 м.; 3) 3 м.; 4) 0,24 м.

Задача № 11.

Малярный валик имеет длину 230 мм, диаметр основания 50 мм. Как узнать площадь поверхности, которую окрасит маляр за один прокат валика? Сколько полных прокатов совершает маляр при окраске за смену 200 м² поверхности.

Задача № 12.

Сколько шпона потребуется для обшивки двух цилиндрических колонн высотой 3,5 м и диаметром 80 см, стоящих в вестибюле здания. На отходы и швы - 10%.

Задача № 13.

На конкурс предоставлено два проекта парников: одного в форме прямоугольного параллелепипеда, другого – в форме полуцилиндра. Определить, какой из них более экономичен по расходу пленочного материала на покрытие, если полезная площадь парников одинакова и равна 10х8 м², а высота каждого 2м.

Тема: «Объем цилиндра»

Задача №14.

Оказалось, что маркировка на технических данных растворосмесителей СО - 80 и С - 863 стерлась. Какие изменения необходимо выполнить, чтобы рассчитать объем раствора в бункере каждого растворосмесителя?

Какая из формул ПRh; ПRL; ПR² h; Пdh в этом случае понадобится?

Задача № 15.

Сколько литров побелки надо налить в емкость для краскопульта диаметром 20 см и высотой 60 см.

Задача № 16.

К электромешалке для приготовления гипсоопилочной мастики прилагаются четыре цилиндрических бачка. За каждый цикл работы заполняются все четыре бачка. Каждый из бачков имеет диаметр 350 мм., и высоту 430 мм. Продолжительность цикла приготовления мастики, включая засыпку и выгрузку, составляет примерно 10 мин. Какое количество мастики можно приготовить в течение 1 часа непрерывной работы?

Задача №17.

Маляру требуется покрыть поверхность общей площадью 200 м². Внутренний диаметр резервуара краскопульта ручного действия приблизительно равен 178 мм., высота- 715 мм. Известно, что при двукратном покрытии расходуется 480 г. краски на 1 м . Рассчитайте, сколько раз и каким количеством водной краски придется наполнять рабочему резервуар, чтобы не оставалось излишков.

Указание. Принять массу 1 л. водной краски равной 1 кг.

Задача № 18.

   При устройстве фундаментов насосной станции строится двухъярусный колодец с круглым основанием. Первый ярус имеет высоту 8,4 м., второй 1,5 м. Определить объем колодца.

Тема: «Объем конуса»

Задача № 19.

На строительных площадках песок хранят в штабелях. После приемки влажный песок уложили в штабель конической формы, размеры которого оказались следующими: длина окружности основания 1 = 32 м., длина по откосу а = 7 м. Определить объем принимаемого песка, учитывая скидку на влажность воздуха 15 %.

Задания для обучающихся по профессии - слесарь по ремонту автомобилей

Тема: «Перпендикулярность прямой и плоскости»

Задача №1

Как проверить, вертикален ли шток поршня в цилиндре двигателя внутреннего сгорания к плоскости тарелки поршня?

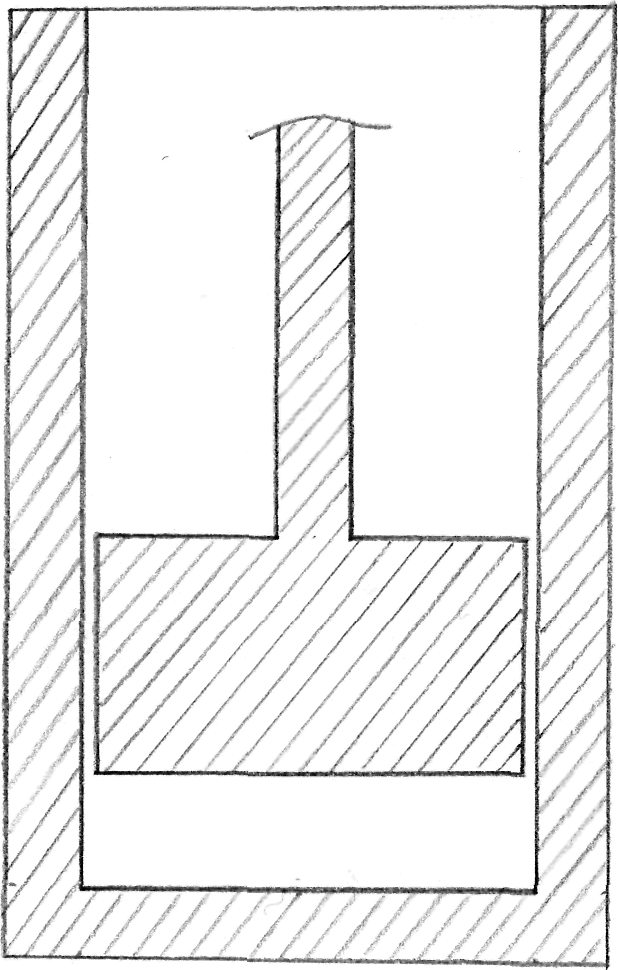
Тема: «Цилиндр»

Задача №2

Втулка сепаратора грузового устройства имеет форму цилиндра, высверленного по оси. Внешний диаметр втулки 20 мм, диаметр отверстия 12 мм, длина втулки 100 мм. Найдите площадь диагонального сечения втулки.

Задача №3

Вычислите полную поверхность клапана двигателя внутреннего сгорания ЯМЗ - 236, если высота его цилиндрической части 30 мм, высота всего клапана 45 мм, диаметр цилиндрической части 1 0 мм, диаметр тарелки клапана 30 мм.

Задача №4

Найти площадь поверхности, которую нужно очистить при ремонте реакционного котла цилиндрической формы, если длина котла 8 м., а диаметр 3,5м.

Тема: «Объем цилиндра»

задача № 5

Чему равен суммарный рабочий объем в дм³ 10 цилиндров двигателя ЯМЗ - 740 (КамАЗ), если диаметр одного цилиндра 120 мм., ход поршня 120 мм?

Задача № 6

Подсчитайте суммарный рабочий объем в дм³ 6 цилиндров двигателя ЯМЗ- 236, если диаметр цилиндра 130 мм, ход поршня 140 мм?

Задача №7

Найдите объем камеры сгорания двигателя автомобиля КРАЗ, если диаметр поршня 100 мм., ход поршня 150 мм?

Задача №8

На сколько увеличится объем камеры сгорания двигателя автомобиля ГАЗ -53, сли диаметр поршня 10 см., ход поршня 9 см?

Тема: «Многогранники»

Задача №9

Размеры кузовов самосвалов МАЗ — 205 и КРАЗ соответственно равны (м):

6,07x2,64x2,44

6,72x2,39x2,18

Какой из них более вместителен?

Задача № 10

Требуется от шабрить боковые грани штока, имеющего форму призмы, в основании которой лежит прямоугольник 12x16 мм. Какой длины должен быть шток, чтобы площадь от шабренной поверхности была 450 мм²?

Задания для обучающихся по профессии - тракторист-машинист сельскохозяйственного производства.

Задача №1.Определим посевную годность семян

Дано: А - чистота семян=90% Б – всхожесть=90% Определить норму высева Q

Решение: Q =(А*Б)/100% = (90*90)/100 = 81%, значит норму высева необходимо увеличить на 19% (100%-81%=19%).

Задача №2.Определить норму высева семян (Н) Дано: пшеница Красноярская А - количество зёрен на 1 га = 7000000шт Д - вес 1000 зёрен = 32 гр Б – всхожесть=90% Определю норму высева семян Н

Решение: Н=(100*А*Д)/Б=(100*7000000*32)/90=248,9(кг/га)

Задача №3.Установка семян на норму высева.

На какую норму высева Р кг/га отрегулирована сеялка, если за п оборотов колеса из неё высыпалось т кг. зерна?

Решение: поскольку площадь S, засеваемая за один оборот колеса сеялки, определяется рабочей шириной сеялки (h(м)) и длиной обода её колеса (С(м)), достаточно знать эти параметры. Так как за один оборот колесо засевает прямоугольник площадью

S=( h*С)/100 (га.)

СhP т

10000 п

то получаю отсюда уравнение Р=(10000т)/Сhп

Найденную таким образом величину сравниваю с нормой высева Н данной культуры и в случае необходимости произвожу дорегулировку для того, чтобы Р было равно Н.

Задача №4 Сено храним в стогах, в скирдах.

Вывести формулу для определения объёма сена в скирде.

Приближенно можно считать, что нижняя часть скирды имеет форму параллелепипеда, а верхняя – полуцилиндра. Для нахождения объёма надо знать длину (с(м)), ширину (а(м)), высоту(в(м)) параллелепипеда, а также радиус цилиндра который равен половине меньшей стороны основания параллелепипеда (а/2).

Формула для вычисления объёма будет иметь вид: V=авс + π(а/2)²с=с(ав + πа²/4)=ас(в + πа/4) Дано: а= 12 м. в= 6 м. с= 38 м.

Решение:

V=12(6+ π*12/4) = 185,04 м³

Задача №5 Вывести формулу для определения объёма сена в стогу.

При вычислении объёма стога сена непосредственно измерить его высоту трудно, поэтому вместо высоты определяют длину перекидки. Можно легко найти длину периметра основания (если стог имеет форму, близкую к форме прямоугольного параллелепипеда) или длину окружности основания, если форма стога близка цилиндрической. Предположив, что стог имеет форму, близкую к прямоугольному параллелепипеду с квадратным основанием. Периметр основания стога равен P(м), а длина перекидки L(м). Тогда объём V стога определяется по формуле (произведение площади основания стога на высоту):

V=(P/4)²H

Неизвестную высоту H выразим через перекидку, используя эмпирическую формулу (Под эмпирическими формулами понимают формулы, которые приближенно выражают зависимость между величинами и установлены опытным путём. Такие формулы находят широкое применение на практике в сельском хозяйстве, для вычисления приближенных значений величин.).

2H + P/4=L

H = 0,5(L - P/4)

Подставляя это значение в формулу объёма, заменяя высоту перекидкой, получу

V=(P/4)² *0,5(L - P/4)= P²(L/32 - P/128)

Если предположить, что форма стога близка к цилиндрической, то получим приближенную формулу

V=L /2 (C/6)² , где С – длина окружности основания стога (м)

Тогда объём сена в скирдах вычислим по формуле

V=(0,52L – 0.45а)ас – эмпирическая формула

Примечание: Если ширина скирды неодинаковая, то надо найти среднюю ширину, изменяя наиболее широкую (верхнюю часть), а затем ширину скирды возле земли. Средняя ширина скирды: а = (а₁+а₂)0,5

Для скирд, имеющих неодинаковую высоту по всей длине, надо найти среднюю длину перекидки, производя три измерения(в концах и по середине скирды). Пусть эти измерения соответственно L_1, L_2, L_3, то средняя длина перекидки будет L=( L₁+ L₂+ L₃)/3

Задачи такого содержания надо уметь решать, чтобы подсчитать количество заготовленного корма в хозяйстве.

 

Задача №6. Время наполнения бункера комбайна зерном (при прямом комбайнировании) вычисляется по формуле:

где р — емкость бункера, ц; b— ширина захвата жатки комбай­на, м; h — урожайность убираемой культуры, ц/га; v — скорость движения комбайна, км/ч. Вычислите время наполнения бункера комбайна зерном при заданных значениях р, b h, v.

Задача №7.Выведите формулу зависимости длины пути, пройденного комбайном до наполнения бункера зерном, от урожайности убираемой культуры.                                       

Задача №8.Трактор стоит 1800 р., а годовая амортизация износа со­ставляет 280 р. Выразите стоимость трактора в зависимости от вре­мени его эксплуатации.

Задача №9. Составьте формулу для вычисления расхода горючего трактором МТЗ-80 при бороновании поля, если на боронование1 га расходуется 1,3 кг горючего. Заполните таблицу.

 

Площадь, га	3	25	43
Расход горючего, кг				1	15	20,2

 

Задача №10.Время наполнения бункера комбайна вычисляется по формуле  . Вычислите время наполнения бункера комбайна СК.-5 «Нива», если ширина захвата его жатки 6,0 м, скорость движения составляет 10,4 км/ч при средней урожайности 25 ц/га.

Задача № 11 Сменная производительность тракторного плуга вычис­ляется по формуле  ,где w— производительность плуга, га; b— ширина рабочего захвата одного корпуса плуга, м; n— число корпусов плуга; v — рабочая скорость трактора, км/ч; f — коэффициент использования времени; t — продолжительность смены, ч. Вычислите сменную про­изводительность пятикорпусного плуга ПЛН5-35, ширина захвата каждого корпуса которого составляет 0,35 м, если средняя ско­рость трактора ДТ-75, работающего на четвертой передаче, сос­тавляет 6,5 км/ч, коэффициент использования времени равен 0,88, а продолжительность смены 8 ч

59