Исследовательская работа "Квадратный трёхчлен"

Введение:

“Главная” функция в школьном курсе алгебры - это квадратный трехчлен. Он присутствует в разных разделах программы. Поэтому необходимо познакомиться с ним поближе и подружиться.

Гипотеза:

Перед работой над этим проектом была выдвинута гипотеза - существует ли связь между коэффициентами квадратного трехчлена с его корнями и знаками этих корней. Давайте проверим верна ли наша гипотеза.

Объект исследования:

Тайны квадратного трехчлена.

Предмет исследования:

Исследование квадратного трехчлена

Цель:

Дополнить уже известные знания о квадратном трехчлене: понятия "квадратного трехчлена"; умение находить корни квадратного трехчлена; формирование навыков самостоятельной работы с большими объёмами информации.

Задачи исследования:

1. Исследование квадратного трехчлена.

2. Как решать квадратные уравнения методом выделения полного квадрата.

3. В чем заключается алгоритм решения квадратного уравнения по формулам.

4.Как решить квадратное уравнение с помощью теоремы Виета.

5. Найти связь между коэффициентами квадратного трехчлена и знаками его корней.

6. Как решать квадратные уравнения с помощью теорем.

Методы исследования:

• Сбор информации

• Обработка информации

• Анализ

• Обобщение

Новизна:

В ходе выполнения проекта расширить свой кругозор о квадратном трехчлене.

Квадратный трехчлен и его корни:

Квадратным трехчленом называется многочлен вида ax² + bx + c, где x- переменная, a, b и c- некоторые числа, причем, a≠ 0. Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю.

Чтобы найти корни квадратного трехчлена ax² + bx + c, необходимо решить квадратное уравнение ax² + bx + c=0.

Динамическая пауза

Задачи на нахождение корней квадратного трехчлена и составление квадратных уравнений встречаются уже в древнеегипетских математических папирусах.

Общее правило нахождения корней и решения уравнений вида:

ax² + bx = c, где a 0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень.

Бхаскара Ачарья (XII в.) сформулировал, соотношения между коэффициентами уравнения. Составил много задач.

«Уравнение - это золотой ключ, открывающий все математические сезамы». С. Коваль.

Впервые ввёл термин «квадратное уравнение» немецкий философ Кристиан Вольф. Он является знаменитым немецким философом, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.

В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов произвел в 1544 году немецкий математик – Михаэль Штифель. Это было настоящее событие в математике.

Способы решения квадратных уравнений:

• применение формул корней квадратного уравнения,

• разложение на множители,

• метод “переброски’ старшего коэффициента,

• на основании теорем,

• метод выделения квадрата двучлена,

• графический метод,

• введение новой переменной.

Энциклопедия квадратного уравнения:

Здесь мы предлагаем вашему вниманию общий вид квадратного уравнения .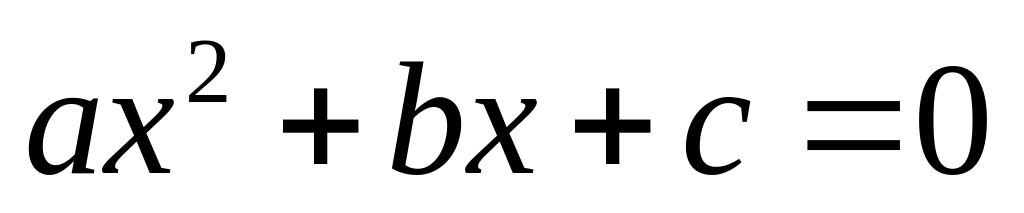

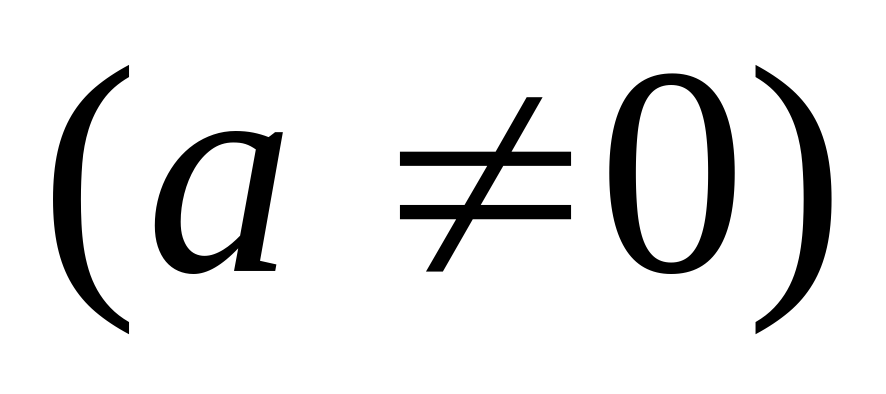Применение формул корней квадратного уравнения.

Знаешь ли ты, что…

Квадратные уравнения возникли очень давно. Еще в Вавилоне около 2000 лет назад до нашей эры. В 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону и Декарту эти формулы приняли современный вид.

Понятие "дискриминант" придумал английский ученый Сильвестр, который называл себя "Математическим Адамом" за то, что придумывал множество терминов.

Как вы думаете, что общего между светофором и дискриминантом?

Дискриминант имеет 3 вида:

• Меньше нуля, красный цвет.

• Равен нулю, желтый.

• Больше нуля, зеленый.

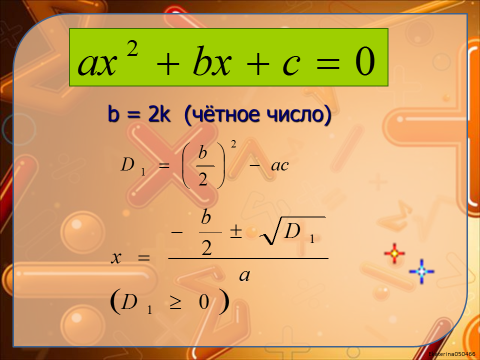
А помогут нам решать приведенные квадратные уравнения с четным вторым коэффициентом мнемонические правила:

• Из «Радионяни»:

«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное q.

• Из «Радионяни» (другой вариант):

p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.

А для теоремы Виеты:

Познакомили поэта
С теоремою Виета
Оба корня он сложил
минус p он получил
а корней произведенье.

Метод выделения квадрата двучлена.

Суть метода: привести квадратное уравнение общего вида к неполному квадратному уравнению.

Метод разложения на множители.

Цель:

привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х) – многочлены относительно х.

Способы:

• Вынесение общего множителя за скобки;

• Использование формул сокращенного умножения;

• Способ группировки.

Введение новой переменной.

Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.

Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Метод выделения квадрата двучлена, метод разложения на множители, введение новой переменной, графический метод, все это изучается в школьной программе.

Особое внимание мы обратим на метод ”переброски” старшего коэффициента.

На основании теорем:

Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен

Е сли в квадратном уравнении a+c=b, то один из корней равен (-1), а второй по теореме Виета равен

Давайте подумаем:

Математик немного поэт. Т. Вейерштрасс

Мыслить последовательно, судить доказательно, опровергать неправильные выводы должен уметь всякий: физик и поэт, тракторист и химик.

Э. Кольман

Задача знаменитого индийского математика XII века Бхаскара.

• Обезьянок резвых стая
  Всласть поевши, развлекалась.
  Их в квадрате часть восьмая
  На поляне забавлялась.
  А двенадцать по лианам
  Стали прыгать, повисая:
  Сколько ж было обезьянок,
  Ты скажи мне в этой стае?

Вывод:

• Наши исследования подтвердили гипотезу проекта. Весь собранный и исследованный материал поможет нам в подготовке к ОГЭ. А так же данный проект можно использовать на уроках математики при изучение тем связанных с квадратным трехчленом.

Мы же продолжим дальнейшие изучения квадратного трехчлена и его применение.

Ну, а закончить мы бы хотели словами Рене Декарта

Мало иметь хороший ум, главное – хорошо его применять.

7

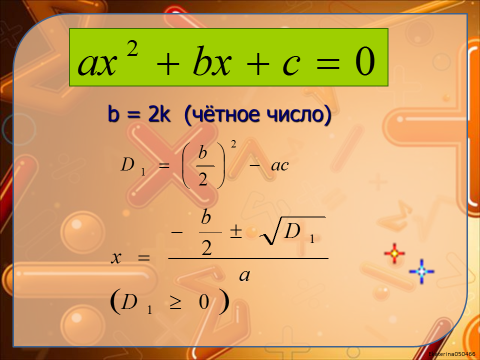
Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 41»

г. Брянска

«О квадратном трехчлене замолвите слово»

Выполнили: ученики 8б класса

Омарова Халида и Будзан Карина.

Руководитель:

Авраменко Любовь Дмитриевна,

учитель математики.

г. Брянск

апрель 2017г.