Исследовательская работа по теме: «Теорема Эйлера и ее приложение

Исследовательская работа по теме: «Теорема Эйлера и ее приложение

Работу выполнила: Климанева Анастасия,

Ученица 10-класса

Проверила: Жовтоног Алина Александровна

История открытия теоремы Эйлера

• Теорема Эйлера была открыта французским ученым Рене Декартом еще в 1640 году, затем забыта более чем на 100 лет и лишь в 1752 году переоткрыта математиком Леонардом Эйлером, имя которого она носит.

Теорема Эйлера

• Теорема Эйлера - математическое утверждение, связывающее между собой число ребер, граней и вершин многогранников. Она хорошо известна и присутствует в продвинутых школьных курсах математики. Но там она используется для выяснения того, какие многогранники могут существовать, поэтому остается невскрытой топологическая сущность этой теоремы и ее роль в классификации поверхностей, не выясняется роль эйлеровой характеристики с родом поверхности .

Леонард Эйлер

Леонард Эйлер – математик, механик и физик. Родился в Швейцарии в городе Базель, в семье небогатого пастора Пауля Эйлера. В конце1726г года Эйлер был приглашен в Петербургскую Академию Наук и в мае 1727 года приехал в Петербург. При жизни им опубликовано 530 книг и статей, а сейчас их известно уже более 800. Причем последние 12 лет своей жизни Эйлер тяжело болел, ослеп на правый глаз и, несмотря на тяжелый недуг он продолжал работать и творить.

Формула Эйлера

• Сумма числа граней и вершин любого многогранника равна числу ребер, увеличенному на 2

• Число граней плюс число вершин минус число ребер в любои многограннике равно 2.

Г + В = Р + 2

Г + В – Р = 2

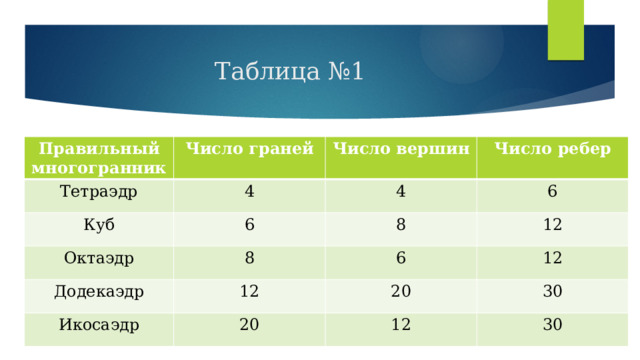
Таблица №1

Правильный многогранник

Число граней

Тетраэдр

4

Число вершин

Куб

Число ребер

4

6

Октаэдр

8

6

8

Додекаэдр

Икосаэдр

12

12

6

12

20

20

30

12

30

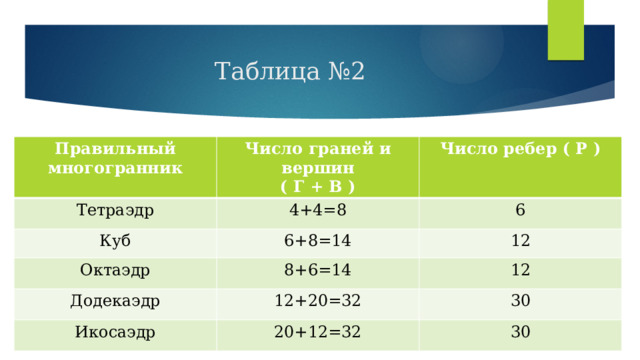
Таблица №2

Правильный многогранник

Число граней и вершин

Тетраэдр

( Г + В )

Число ребер ( Р )

4+4=8

Куб

6+8=14

6

Октаэдр

Додекаэдр

12

8+6=14

12+20=32

12

Икосаэдр

30

20+12=32

30

Утверждения

1)Число вершин, увеличенное в 3 раза, больше либо равно числу ребер увеличенному на 6.

2)Число граней, увеличенное в 3 раза, больше либо равно числу ребер увеличенному на 6.

3)У всякого многогранника есть хотя бы одна треугольная, четырехугольная или пятиугольная грань, а также хотя бы один трехгранный, четырехгранный или пятигранный пространственный угол.

Упражнение №1

• Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет : а) 12 ребер ; б) 15 ребер?

• Ответ: а) В=6, Г=8; б) В=7, Г=10.

Упражнение №2

Посчитайте число вершин , ребер и граней у многогранника. Выполняется ли для них равенство Эйлера?

Ответ: В=12, Г=8;. Р=18; Да

Вывод:

• Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.

Топология

• Топология – раздел математики, занимающийся изучением свойств фигур ( или пространства),которые сохраняются при непрерывных деформациях, таких, например, как , растяжение, сжатие или изгибание.